高层建筑用钢的热塑性变形行为研究

由 尧

(淮北职业技术学院 建筑工程系，安徽 淮北 235000)

随着国民经济实力的增强和城市化进程的不断推进，我国建筑工程正逐步朝着超高层和大跨度钢结构方向发展，这给建筑新技术和新材料带来了巨大发展机遇。高建钢作为受力情况复杂的高层建筑、大跨度体育场馆以及钢结构厂房等大型建筑工程中重要的结构材料，除需要具有传统普碳或者低合金钢的强度、塑性和抗震防火性能外[1]，还需要具有良好的成形性以满足超高层和大跨度钢结构建筑的需求，而实际生产过程中高层和大跨度建筑用钢存在加工困难、生产成本高以及综合性能难以满足高层建筑用钢要求等问题[2-4]。虽然科研工作者和生产厂家在原材料开发和生产工艺优化上做了大量工作，但是关于高层建筑用钢热塑性变形方面的研究较少。通过热模拟的方法研究高层建筑用钢的组织和性能变化规律，可以对Q460高建钢热变形过程中的显微组织演变进行模拟分析，确定动态再结晶的发生条件，并为制定和优化Q460高建钢热辗扩工艺提供参考依据。

1 试验材料与方法

以砂型铸造Q460高建钢钢坯为试验原料，原始组织为铁素体和珠光体，采用电感耦合等离子发射光谱法测得高建钢主要元素化学成分见表1。

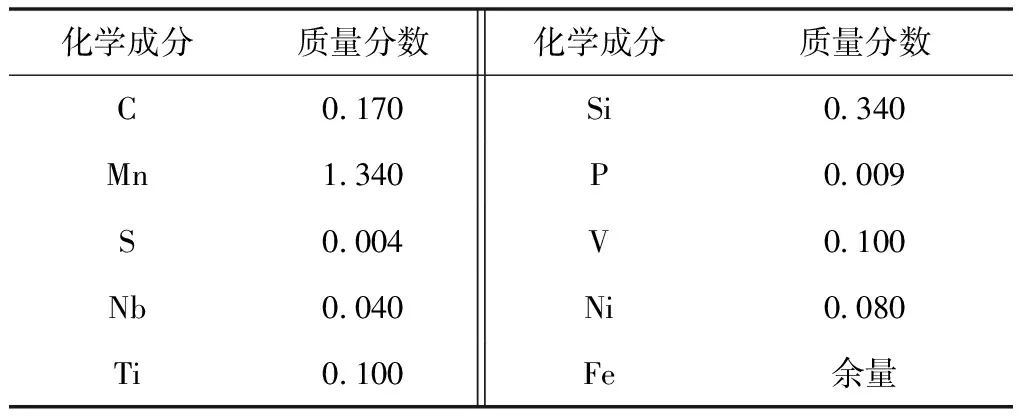
表1 高建钢主要元素化学成分 %

砂型铸造Q460钢的热压缩试验在Gleeble-3800型材料热模拟试验机上进行，用于热模拟的圆柱试样截取自Q460高建钢钢坯，圆柱试样直径8 mm、高12 mm，热模拟变形过程中在圆柱试样两侧放置厚度0.15 mm的石墨片，图1为Q460钢的热压缩工艺示意图。

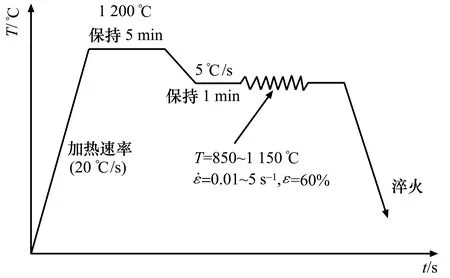
图1 Q460钢的热塑性变形工艺图

2 试验结果与分析

2.1 真应力-真应变曲线

图2为Q460钢的应力-应变曲线。当变形温度为850，950，1 050，1 150 ℃时，Q460钢的应力都会随着应变增加而出现先增加、后稳定的趋势，这是因为在变形开始阶段，较小的应变下会发生位错缠结而加工硬化[5]，应力增加速率较快，而当应变增加至一定程度时，应力对应变的敏感性降低，整体应力趋于不变，这个阶段会在Q460钢内部同时发生动态回复和动态再结晶，硬化与软化相互作用。此外，在相同的应变和变形温度下，变形速率的增加会使得Q460钢具有较高的应力，这主要与加工硬化程度有关[6]。

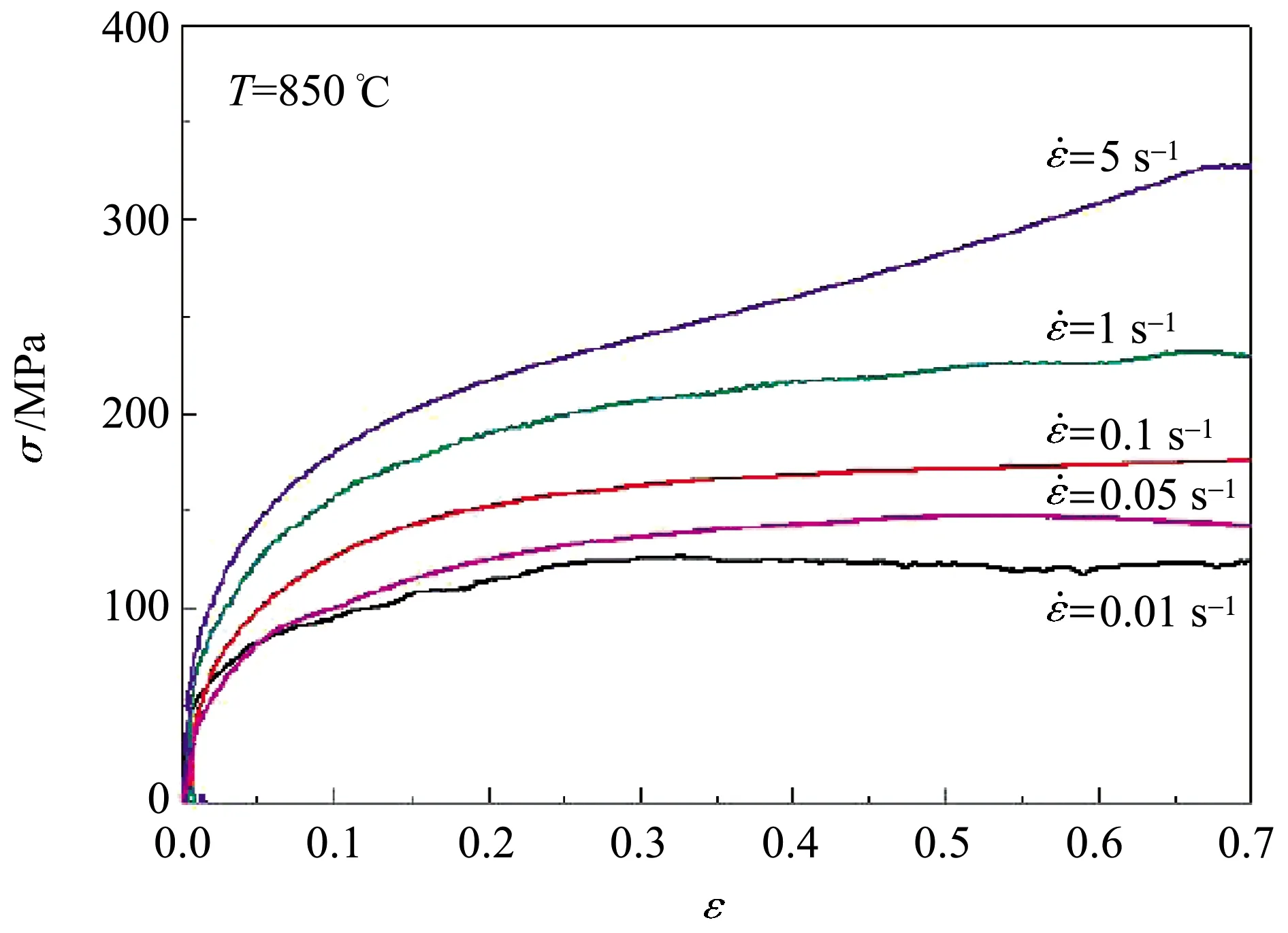
(a)850 ℃

2.2 Q460钢的动态再结晶动力学方程

Q460钢在变形温度为850，950，1 050，1 150 ℃，应变速率为0.01，0.05，0.10，1.00，5.00 s-1时会发生动态再结晶，Q460钢的临界应变εc和峰值应变εp存在如下关系[7]：

εc=0.83εp。

(1)

在热压缩变形过程中，如果Q460钢已经发生动态再结晶，稳态应变εs、εp和临界应力σc可表示为[8]：

εp=K1Zm1，

(2)

εs=K2Zm2，

(3)

σc=K3Zm3。

(4)

式中：Kn(n=1，2，3)和mn(n=1，2，3)为与Q460钢有关的材料常数。

图3为Q460钢的热压缩曲线关系图，通过对曲线进行线性拟合后可得出Kn(n=1，2，3)和mn(n=1，2，3)[9]，将Kn(n=1，2，3)和mn(n=1，2，3)数值代入公式(2)～(4)，可得：

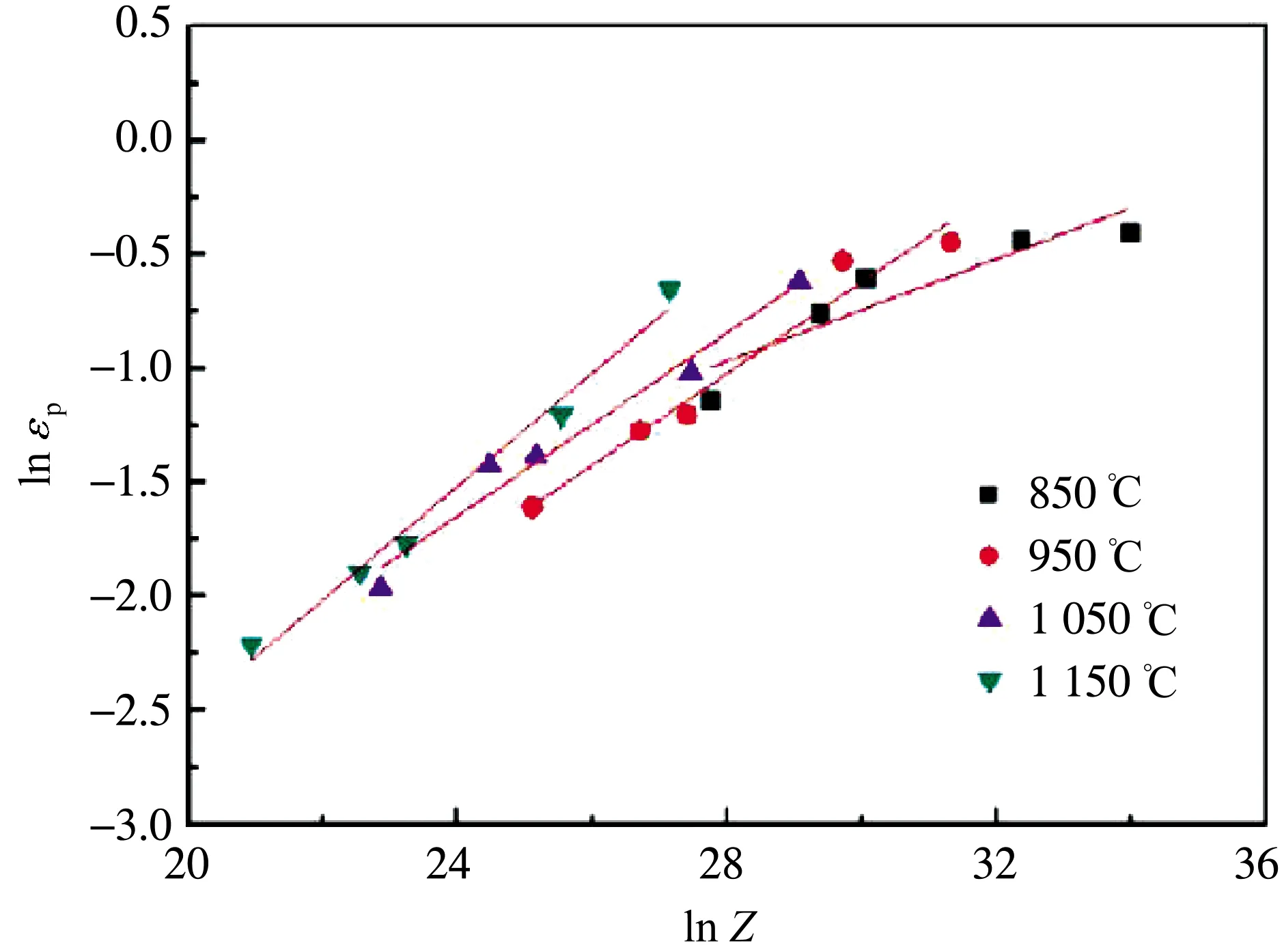
(a)ln Z-ln εp

εp=0.002 078Z0.190 6，

(5)

εs=0.029 65Z0.104 4，

(6)

σc=2.652Z0.162 3。

(7)

图4为Q460钢的加工硬化率θ与应力σ关系曲线，其中θ=dσ/dε。当变形温度为850，950，1 050，1 150 ℃时，Q460钢的加工硬化率θ会随着应力增加而逐渐减小；在相同应力下，应变速率越大则加工硬化率越大；此外，当变形温度为950 ℃时，应变速率0.01，0.05，0.10 s-1时会产生饱和应力，在变形温度为1 050 ℃和1 150 ℃时，低应变速率下同样会产生饱和应力，这主要是因为Q460钢热变形过程中会发生动态回复与动态再结晶所致[10-11]。

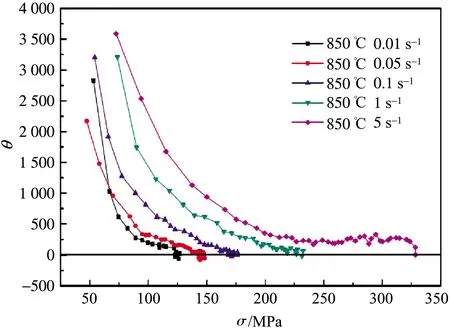
(a)850 ℃

表2为Q460钢的饱和应力σs值统计结果。由表2可知，随着应变速率增加，相同变形温度下Q460钢的饱和应力σs值逐渐增大，“—”表示不存在饱和应力。

表2 Q460钢的饱和应力σs值统计结果

引入Zener-Hollomon因子Z来进一步研究Q460钢的热压缩变形行为，Z的表达式为[12]：

(8)

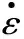
由式(8)可以绘制Q460钢热变形过程中的Z因子与饱和应力σs和稳态应力σss关系曲线，如图5所示。

(a)ln Z-ln[sin h(ασs)]

变形温度为850，950，1 050，1 150 ℃，应变速率为0.01，0.05，0.10，1.00,5.00 s-1时，Q460钢的饱和应力σs和稳态应力σss的动力学方程为：

Z=9.165×1 011[sinh(0.007 69σs)]5.427 9，

(9)

σs=130.04sinh-1(1.091×10-12Z)0.184 2，

(10)

σss=130.04sinh-1(9.039×10-13Z)0.218 1。

(11)

2.3 动态再结晶运动学方程

在Q460钢热压缩过程中，动态再结晶运动学方程可以表征动态再结晶发生的程度，在一定时间内Q460钢的动态再结晶体积百分数XDRX可用下式求解[13]：

加强地质研究，核查有利区域。青海油田在涩北剩余气富集区部井。针对气藏水侵面积扩大、水淹状况复杂、剩余气分布规律认识不清等问题，通过开展气藏精细描述，逐层研究水侵区域过路新钻井电性变化特征，及时跟踪气藏动态，开展生产历史拟合等方式，摸排剩余气富集区。

(12)

(13)

式中：kd和md为与Q460钢有关的常数；ε0.5为材料发生50%动态再结晶时对应的应变；A1为应变速率指数；QDRX为动态再结晶激活能，J/mol。此外，XDRX还可以表示为[14]：

(14)

式中：σWH为加工硬化部分应力的外延，MPa。根据图2确定σWH并结合饱和应力σs和稳态应力σss值，将XDRX=50%代入式(14)即可求得Q460钢在发生50%动态再结晶时的瞬态流变应力，由此可以对应得到此时的ε0.5，统计结果见表3。

表3 砂型铸造Q460钢的ε0.5

对式(13)两边取对数，可得：

(15)

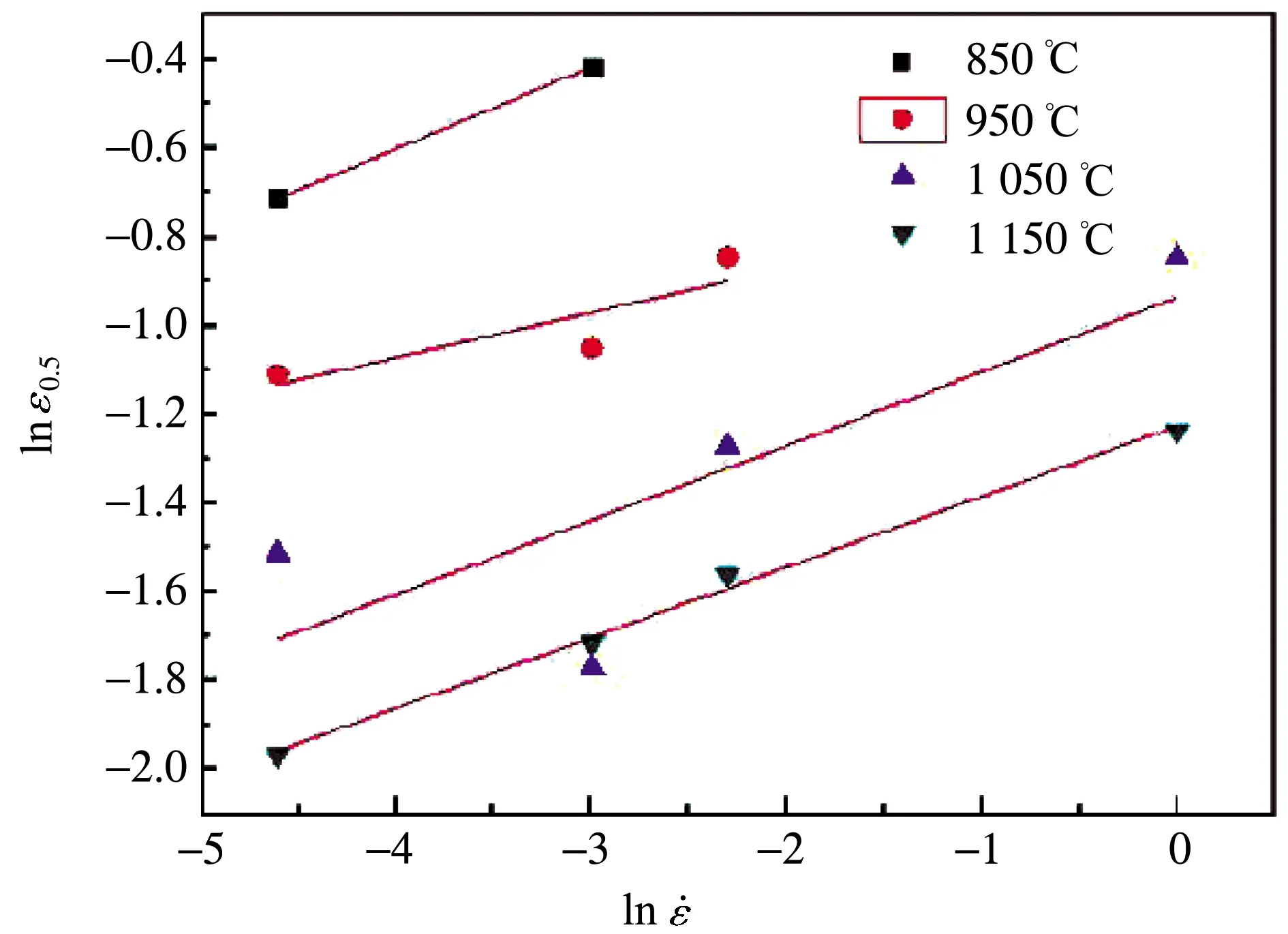
(16)

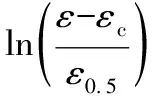
图7 Q460钢的ln[-ln(1-XDRX)]与关系图

(17)

图8为Q460钢的动态再结晶体积分数关系曲线。不同热变形条件下Q460钢的动态再结晶体积分数曲线都大体呈“S”型，在如变形温度为1 150 ℃时，应变速率0.01 s-1和0.10 s-1时的临界应变分别为0.09和0.14；而当变形温度为950 ℃时，应变速率0.01 s-1和0.10 s-1时的临界应变分别为0.17和0.26。可见，Q460钢的动态再结晶体积分数会随着变形温度和变形速率的不同而发生变化，要想获得具有较高体积分数的动态再结晶，在实际热加工过程中可以选择高温和低应变速率，这主要是因为此时Q460钢会具有较小的Z，相应发生动态再结晶的临界应变更小[16-18]。

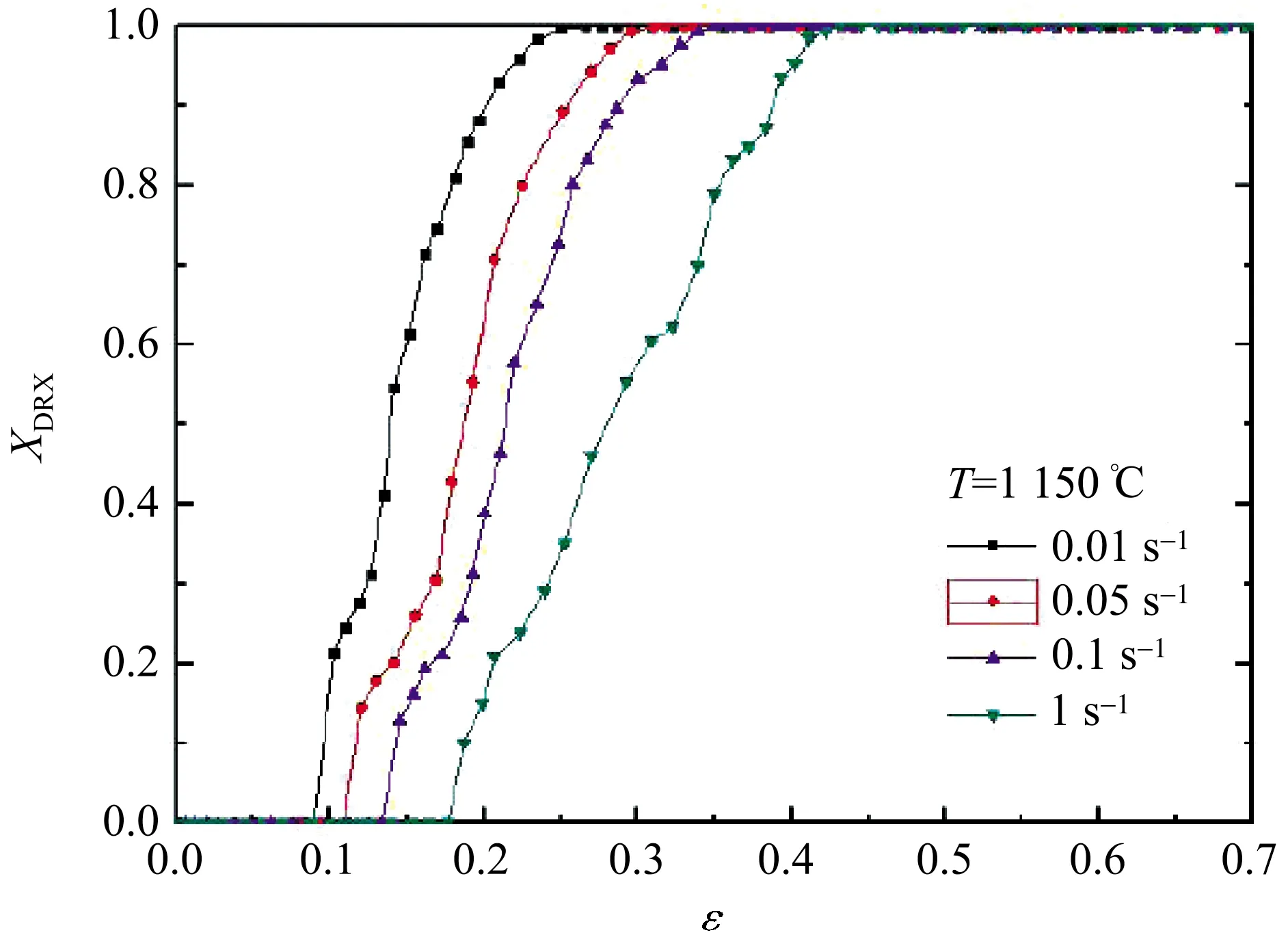
(a)1 150 ℃

2.4 动态再结晶晶粒尺寸方程

Q460钢热变形过程中的动态再结晶晶粒大小DDRX可表示为[19]：

(18)

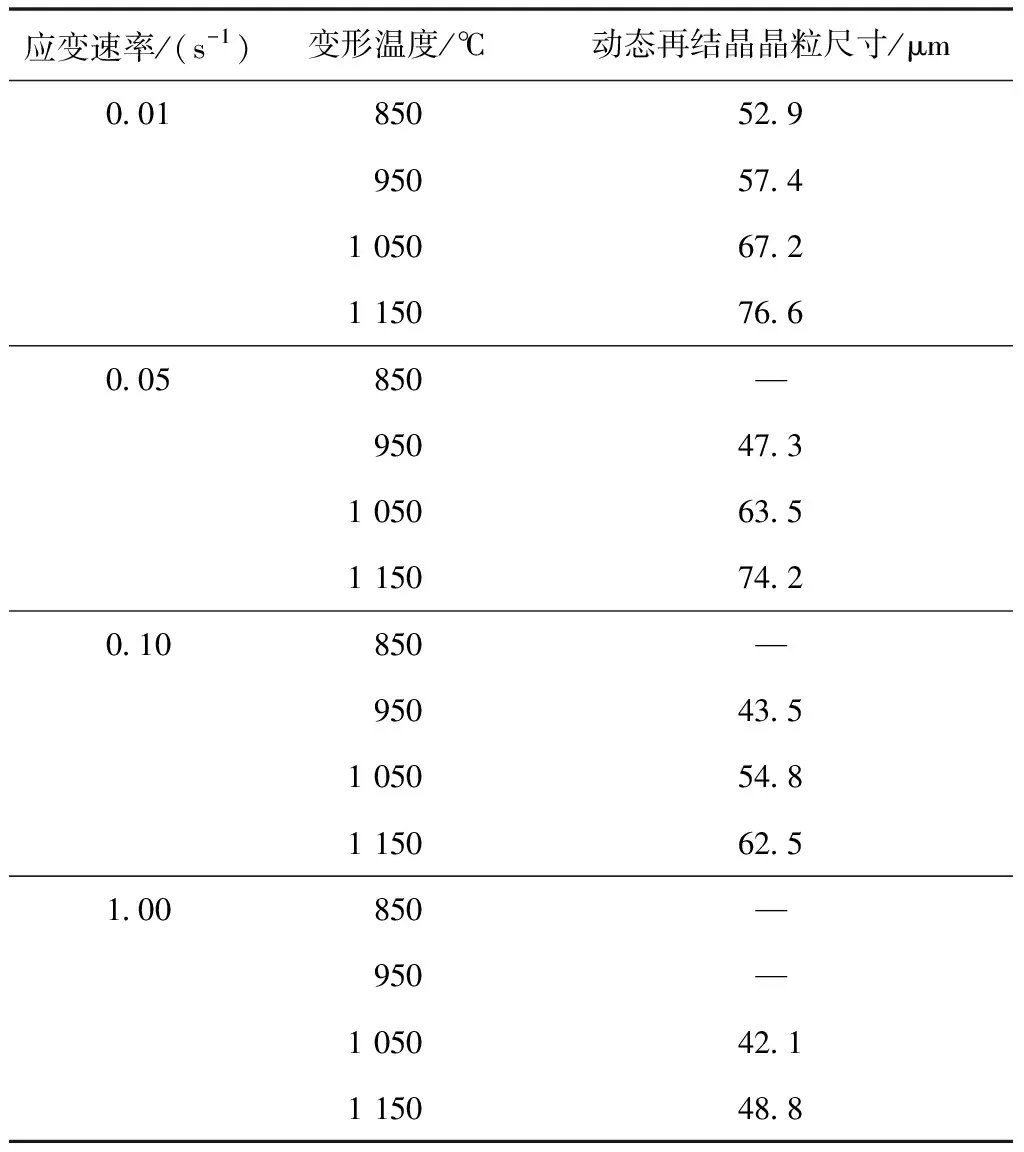
表4 Q460钢的DDRX值

由此，砂型铸造Q460钢的动态再结晶尺寸可以表示为：

DDRX=453.05Z-0.083 6。

(19)

在对高层建筑用Q460钢进行热加工过程中，可以通过改变变形温度和变形速率来改变Z值，从而影响Q460钢的再结晶晶粒尺寸，通过微观组织调控来实现高强塑性建筑用钢的生产。

3 结论

1)Q460钢的动态再结晶动力学方程为：

σs=130.04sinh-1(1.091×10-12Z)0.184 2，

σss=130.04sinh-1(9.039×10-13Z)0.218 1。

2)砂型铸造Q460钢动态再结晶运动学方程为：

3)砂型铸造Q460钢动态再结晶晶粒尺寸方程为：

DDRX=453.05Z-0.083 6。

4)Q460钢的动态再结晶体积分数会随着变形温度和变形速率的不同而发生变化，要想获得具有较高体积分数的动态再结晶，在实际热加工过程中可以选择高温和低应变速率。可以通过改变变形温度和变形速率来改变Z值，从而影响Q460钢的再结晶晶粒尺寸。