浅谈数据处理在CUMCM高职数学建模中的应用
◎白 余
(昆明铁道职业技术学院,云南 昆明 650000)
一、引言
CUMCM全称为China Undergraduate Mathematical Contest In Modeling,即全国大学生数学建模竞赛.赛题内容涉及工业、经济、医疗、环境、资源、管理等众多领域,参赛者囊括了各本科及专科院校的在校大学生.数学建模是从实际问题出发,通过数学语言对实际问题进行简化、抽象和描述,根据某种定律建立变量和参数间的数学关系(即数学模型),再利用计算机软件对该数学模型进行分析和求解,并对求解出的结果进行分析和检验,最终找到解决实际问题的方案.在赛题中经常会提供出大量信息或海量数据,从这些问题中寻求所需问题的答案就是数据建模.对大量实验数据进行处理,就需要利用计算机软件来辅助以快速整理和分析,这一过程即为数据建模中的数据处理.即利用一定的处理方法从海量数据中发现其内在规律,甚至找出表面上看起来毫无关联的数据之间的内在关系.
从CUMCM(专科组)近六年的赛题来看(见表1)每年至少有一道赛题涉及数据分析及数据处理.本文以部分真题为例介绍了Excel数据处理方法及Matlab数据处理在高职数学建模竞赛中的应用.

表1 CUMCM(专科组)部分赛题表
二、数据处理
1.Excel数据分析
数学建模竞赛题目给出的原始数据大多数都是以Excel文件的形式保存.Excel软件具有数据格式化、数据排序筛选分类汇总、公式与函数的应用、可视化分析各种图表、数据透视表与数据透视图等诸多功能,可用来对数据进行分析与处理.如按关键字排序,按指定条件筛选数据,按不同类别汇总数据,快速计算最值、和值、均值、方差,快速绘制散点图、折线图、直方图,对数据的变化趋势进行观察分析,等等.
例如2019年D题——空气质量数据的校准.空气污染对生态环境和人类健康危害巨大,通过对“两尘四气”(PM2.5、PM10、CO、NO2、SO2、O3)浓度的实时监测可以及时掌握空气质量,对污染源采取相应措施.现提供一段时间内某个国家监测控制站点(国控点)每小时的数据和该国控点近邻的一个自建点数据(相应于国控点时间且间隔在5分钟内),要求对自建点数据与国控点数据进行探索性数据分析,并监测温度、湿度、风速、气压、降水等气象参数对空气质量的影响.
从附件1、2中删掉测量数据差异性较大的部分,选取时间相近、次数较为匹配的数据作为研究对象,根据监测数据计算出每一天国控点和自建点每个空气质量浓度的数据平均值,通过Excel图表制作出国控点和自建点的空气质量浓度折线图及柱状图(见图1、图2),就可以直观地进行国控点数据和自建点数据初步的差异性和相关性分析.

图1 PM2.5国控点与自建点的浓度数据对比图

图2 PM2.5浓度平均值与温度平均值的关系对比图
由图1可知,自建点的PM2.5浓度普遍高于国控点的PM2.5浓度,根据问题信息我们了解到国控点的布控较少且花费较大,不能够实时大范围的监测到PM2.5的浓度数据,故国控点的浓度数值普遍较低,国控点的PM2.5浓度监测平均值最低达到19.46 μg/m3.根据图2,我们可以知道温度与PM2.5浓度在2019年1月3日-2019年3月14日的变化关系.
2.Matlab数据拟合
在数学建模竞赛中经常会用数据拟合进行数据处理.在生产和科学实验中,很多实际问题的观测数据并不完全在一条直线上或曲线上,即不能直接写出自变量与因变量关系的函数表达式.那么如何根据散点图的变化趋势,选定一条曲线近似表达数据的相互关系呢?解决的办法就是根据散点图的变化趋势选定近似函数y=φ(x),不要求它通过所有已知样本点,但要求在某种准则(如最小二乘法)下让这个近似函数与这些散点最为接近或总偏差最小,即数据拟合.数据拟合可分为多项式函数拟合、非线性拟合.在Matlab中可通过命令Polyfit( )、Polyval( )和Lsqcurvefit( )或Matlab曲线拟合工具箱cftool实现.命令的调用格式为:
polyfit(x,y,n);
polyval(p,x);
Lsqcurvefit(fun,x0,xdata,ydata)
为了确定适合拟合的模型,一般先做散点图观察数据的分布情况再确定模型的选取.
例如2018年C题——大型百货商场会员画像描绘.在零售行业中,会员价值体现在持续不断地为零售运营商带来稳定的销售额和利润,同时也为零售运营商策略的制定提供数据支持.零售行业会采取各种不同方法来吸引更多的人成为会员,并且尽可能提高会员的忠诚度.结合附件数据针对会员的消费情况建立能够刻画每一位会员购买力的数学模型,以便能够对每个会员的价值进行识别.
为了刻画出每一位会员的购买力,可建立会员购买力与会员会龄的数学模型X(t)=f(t).根据题目附件选出在一定时间内所有会员在同一时间的购买数据进行整理分析,得到会员购买力数据采样表(见表2),并进行Matlab曲线拟合.
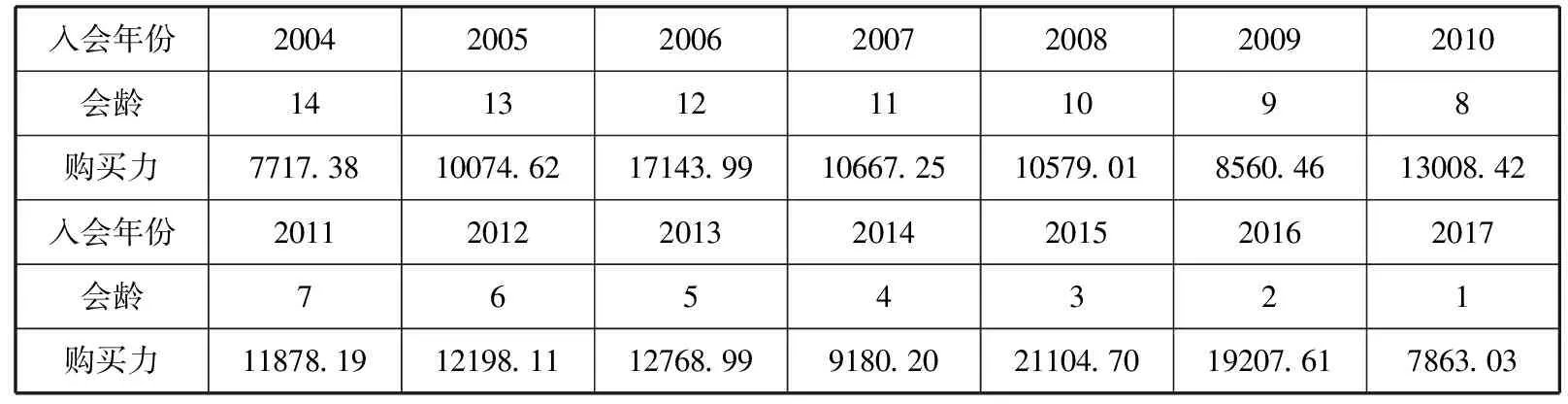
表2 会员购买力数据采样表
t0=[14 13 12 11 10 9 8 7 6 5 4 3 2 1];
y0=[7717.38 10074.62 17143.99 10667.25 10579.01 8560.46 13008.42 11878.19 12198.11 12768.99 9180.20 21104.70 19207.61 7863.03];
n=10;
p=polyfit(t0,y0,n)
tt=1:0.1:14;
yy=polyval(p,tt);
plot(tt,yy,’-b’,t0,y0,’.r’,’Markersize’,20)
legend(’拟合曲线’,’原始数据’)
xlabel(’会龄’);
ylabel(’购买力’)
运行该程序得到如下拟合函数及拟合图像(见图3)

图3
X(t)=-0.0005t7+0.0062t6-0.0471t5+0.2308t4-0.7150t3+1.3134t2-1.2576t+0.4777
本次拟合采用了10次多项式拟合,从图像上分析大部分原始数据都经过了拟合函数,其余数据点和拟合函数满足最小二乘法则,故拟合效果较好.
3.Matlab数据插值
当受实验条件限制或实验数据量不足时,在已有数据可信的基础上,通常利用函数插值方法插值出两数据点之间的一系列数据点,所绘制的数据曲线会严格的经过每一个实验数据点.这就是数据插值.如信息技术中的图像重建、图像放大过程中为避免失真而做的插值补点等.常用的插值法有拉格朗日多项式插值、牛顿插值多项式、分段线性插值、样条插值.Matlab提供的插值函数有interp1( )、interp2( )等命令分别可进行一维插值、二维插值……n维插值,其调用格式为:
yi=interp1(x,y,xi,’method’);
z=interp2(x,y,z,x0,y0,’method’)
如在1994年赛题计算山体海拔高度中用到了数据插值方法,2005年赛题雨量预报的评价也用到了插值计算.
4.Matlab回归分析
变量之间的关系大致分为两类,一类是确定性的关系,另一类是非确定性的关系.对于某些非确定性关系,当自变量x确定后,因变量y的值并不随之确定,而是按照一定的统计规律取值.我们将它们之间的关系表示为y=f(x)+ε,其中f(x)称为回归函数,ε称为随机项.这样的数据分析即为回归分析.回归分析不仅可以揭示自变量对因变量的影响大小,还可以用回归方程进行预测和控制.回归分析按照涉及变量的多少可分为一元线性回归、多元线性回归.Matlab软件中的regress( )、nlinfit( )、stepwise( )命令即可实现,其调用格式为:
[b,bint,r,rint,stats]=regress(y,x,alpha);
[b,r,J]=nlinfit(x,y,’model’,b0);
rcoplot(r,rint);
stepwise(x,y,inmodel,alpha)
例如2016年C题——铅酸电池作为电源被广泛用于工业、军事、日常生活中.在铅酸电池以恒定电流强度放电过程中,电压随放电时间单调下降,直到额定的最低保护电压.在电流为50 A时,测得电压x和放电时间y的数据如表3所示.请建立放电时间随电压变化的回归模型.

表3 铅酸电池电压x和放电时间y的数据表
首先把数据导入Matlab,再输入如下程序:
figure(1);
scatter(x,y)
xlabel(′x(电压)′)
ylabel(′y(时间)′)
X=[ones(length(y),1),x];
[b,bint,r,rint,stats]=regress(y,X);
figure(2);
rcoplot(r,rint)
运行结果、散点图及残差图如下所示(见图4、图5).

图4 散点图

图5 残差图
b=1.0e+04 * 1.9703 -0.1870
bint=1.0e+04 * 1.8833 2.0573 -0.1953 -0.1787
stats=1.0e+03 * 0.0010 2.3417 0.0000 0.0006
从各项参数及散点图来看回归模型显著,但从残差图来看第七个数据异常,多次删除异常数据后再运行程序,运行结果及残差图、拟合图(见图6、图7)效果较好.

图6 残差图

图7 拟合图
b=1.0e+04 * 1.9611 -0.1861
bint=1.0e+04 * 1.9162 2.0061 -0.1904 -0.1818
stats=1.0e+03 * 0.0010 9.1470 0.0000 0.0001
因此时间随电压变化的回归模型为:
y=19611-1861x
三、结语
当下是信息爆炸的时代,大数据应用于生产生活的各个领域.数据处理在高职数学建模中亦发挥着非常关键的作用,合理选择数据处理方法能提高数据分析的准确性.借助相关数学软件(Excel、Matlab、Python、SPSS等)进行数据处理可大大提高数学建模的效率.

