更新教学素材，开展课程思政，提高高等数学课堂教学效率

◎周子健 海 昕

(国防科技大学文理学院，湖南 长沙 410072)

高等数学作为我国高校理工类各专业的公共基础课，通常被安排为新生开学的第一门课，它不仅承载着夯实学生后期专业理论研究和实验研究数学基础的重任，而且在学生数学素养和创新精神培育、逻辑思维能力提升方面发挥着独特作用.

作为高等数学主要内容的微积分，在传统教学中其应用大多由求解物体运动速度与加速度、计算平面图形面积、计算三维物体体积以及经济学中收益函数求最值等问题构成.如今人工智能、机器学习、高性能计算等热点技术应用于社会发展各个领域.微积分其求解任意连续问题的“分割、求近似、求和、取极限”的思想被越来越多的学者借鉴，用以深入研究各类日益复杂的系统.将高等数学推动热点技术发展的实例作为教学素材，既能激发学生学有所用的兴趣、服务社会的意识，也是教师落实习近平总书记“希望广大教师不忘立德树人初心，牢记为党育人，为国育才使命”指示，将课程思政融入教学的高度体现.我们根据学生特点在高等数学的日常教学中将新兴技术应用及课程思政融入课堂，已取得了一定成效.

一、高等数学课程学情分析

随着技术进步和时代发展，高等数学课程也同其他专业课程一样，采用了线上线下混合教学的教学模式.同时随着教学理念的不断革新，也促使着教师们转变为以学生为中心，并根据学生特点设计教学内容、革新教学方式.

(一)学生思想活跃，获取信息渠道广，对传统教材内容兴趣较低

高等数学授课对象为刚进入大一的新生，千禧年之后出生的他们思想活跃、接触面广，往往较早就接触到了智能设备，如手机、平板、无人机等.这使得学生对新兴技术抱有极大兴趣，如基于微分方程的自动驾驶控制策略、基于微分思想的短视频分享平台下自动推荐视频算法、基于高性能计算的天气预报和基于曲率计算的高铁限速标定等.同时，学生对热点技术背后的数学原理了解不多，渴望通过学习寻求解答.

现有的高等数学课程，虽然已经开始引入小班教学，采用线上线下混合教学的模式，但是教学内容的许多素材往往相对老旧，与现代社会发展和实际应用需求有较大差距；部分例子较为抽象，难以理解，不能联系日常生活，较难在日常课程教学中引起学生的共鸣，激发学生的求知欲望.

(二)线上教学平台利用不充分

随着疫情的不断反复，线上平台基于其便利性被应用于日常各个学科的教学中.但大部分线上教学仅仅是基于线上平台发布教学任务、共享教学资料、授课、测评，并未充分利用线上日新月异的教学资源.而线上资源虽浩瀚无垠，但缺乏条理，较为杂乱，内容也良莠不齐，真实性和准确性难以辨别.故学生即使想利用线上资源学好高等数学，也会因为缺乏高效的检索手段和强大的辨别能力，导致学习效率不高.部分优质平台和资源学生甚至不知其存在，合理利用更无从谈起.

此外，现有的线上平台以教师发布教学任务，学生跟进进行学习为主，并没有利用线上平台可以相互交流的特性，学生偏向于打卡式学习，难以达到较好的学习效果.线上平台缺乏互助讨论的专区，学生们无法通过在线提问、交流系统地梳理所学内容，也缺少教师的加入来确保讨论结果的正确性.

(三)应试教育导致学生习惯于被动式学习，自主学习能力不足

中学阶段大多采用以考试成绩为主的结果性导向评价体系，忽略了对学生能力的培养.学生在这样的评价方式下，习惯于死记硬背的被动式学习，自主学习的能力没有得到充分锻炼，缺乏独立查阅资料、集体讨论、严谨研究的能力.教师上课也以灌输式教学为主，学生在教学过程中只能按照教师预先设计的思维方式去思考，导致学生自主学习的动力不足，思维方式容易单一化，缺乏创新性.

进入大学阶段，高等数学的知识点较多、课时紧张，其学习注重思维的训练，需要学生有很强的自主学习能力，成为学习的主导者.而沿用中学阶段学习模式的新生，由于内驱力不足，缺乏自主学习的动力，就会较难跟上学习进度.

二、热点技术背后的高等数学

传统高等数学教材和配套习题中，较少涉及新兴技术领域背后的高等数学知识，也并未说明高等数学是如何服务应用于现在被广泛使用的软硬件中的，如自动驾驶和微分方程的联系、机器学习与微分思想的联系、天气预报与高性能计算和偏微分方程的联系、高铁速度和曲率等.下面我们以这四个方面为例，探讨高等数学在热点技术领域的应用.

(一)自动驾驶与微分方程

微分方程作为高等数学的课程内容，其公式推导较为复杂，计算难度大.在教学过程中，学生易产生畏难情绪，从而掌握不好该知识点.在学习微分方程时，教师可以向学生提出这样的问题：“现在汽车进入了电动化时代，而电动汽车区别于汽油车的一大特点就是具有自动驾驶的潜能.而自动驾驶领域的控制策略就包含了比例积分微分控制，简称PID控制，其控制输出信号可以写成如下函数：

其中Kp,Ti,Td为可调参数，e(t)为t时刻的偏差度量.那么PID控制器是如何控制汽车的呢？”

学生通过研究上述函数可以发现，根据输出信号函数u的形式，PID控制可以在知晓汽车位置、速度、角度偏差的情况下，自动完成汽车车辆的控制.学生在对这一部分内容产生兴趣之后，回忆平时乘坐汽车的情形，会思考在特殊的自动驾驶场景(路况特殊情形、道路有横风情形)下PID是如何给出最优控制策略的.这也是微分方程的求解和积分计算问题.最终，学生通过挖掘、解决自动驾驶背后的数学问题，激发了学习兴趣，也提升了自主学习能力.

随着无人机进入消费领域，无人机开始被广泛应用于灯光秀表演、小型货物运送、地形地貌勘探、广告投放和信息发布等事宜中.除此之外，现在越来越多的学生也都购置了无人机用于摄影取景、短视频拍摄等.教师可以以此引导学生思考这样的问题：“无人机在空中是如何保持姿态并且实现自动返航的呢？”另外，在国家重大节假日和城市文化庆典活动中，都会使用无人机群进行灯光演出.老师进一步提出问题：“如何控制大量的无人机进行悬停、控制变换姿态以展示不同的动画效果呢？”

学生通过查阅相关资料可以发现，无人机姿态控制可以由姿态微分方程刻画，这是通过求解由欧拉角变化率为未知量的欧拉运动方程得到的.而无人机群的控制也能通过求解微分方程来实现.查阅资料、挖掘无人机背后控制机理的过程，将开阔学生的视野，提升其科学研究能力.

微积分相关内容在热点科技的应用，既是高等数学在新时代技术中的体现，也是课程思政的一种载体.随着汽车电动化浪潮的到来，教师可以向学生介绍高等数学是如何服务于自动驾驶技术的和我国自主品牌在自动驾驶领域取得的成就，并向学生分享国内造车新势力突破国外自动驾驶巨头公司专利壁垒，自主构建自动驾驶技术路线的故事.同时，可以介绍国内无人机独角兽公司通过技术创新，被称为我国无人机发展强劲助推器的故事，以此增强学生的民族自信心.

(二)机器学习与微分思想

函数的微分是不定积分和定积分的重要基础，也是高等数学的重要概念之一，学生在学习时往往对于背后的微分思想——函数在局部是否可以用线性函数进行逼近掌握得不够深刻.在学习多变元微分时，教师可以提出如下问题：“谷歌旗下公司发布的阿尔法围棋(AlphaGo)利用机器学习算法，自学围棋，并接连击败了人类中顶尖的棋手，其中包括世界排名第一的我国棋手柯洁.而机器学习技术本身应用了高等数学的微分思想，那该思想是如何服务于机器学习的呢？”

学生通过检索资料可以发现，机器学习的核心思想是在一定约束条件下求一个多元函数的最值.其利用了高等数学中函数可微的性质，可以用如下式子来刻画.

f(x+ε)=f(x)+(∇f(x),ε)+||o(ε)||.

机器学习求解最值的过程是从某个点的函数值出发，通过多次微小的改变进行最佳的优化或线性逼近.而这里微小的改变则指的是自变量增量ε.对于机器学习算法中考虑的函数f(x)，通过微小改变获得最佳线性逼近的方向无疑是当前点方向导数.这一思想的应用将加深学生对多变元函数微分和方向导数的理解，拓宽其思维，增加其探索新知识、解决实际问题的动力.

此外，教师可以在课程中引导学生作出如下思考：“大家都有在网上购物的经历.在购物平台搜索商品时，我们发现位于搜索页面前几的商品大都符合我们的预期，那么购物平台是如何对不同个体有针对性地推送商品，而且商品的种类、价格、性能又能满足这些个体的需求呢？”

学生通过检索后可以发现，购物平台会基于机器学习分析消费者以往的消费数据，基于消费水平和商品喜好对人群进行分类.通过比对消费水平和商品喜好相似消费者的已购商品，对搜索结果进行优化排序并呈现给搜索者，并针对搜索者的点击反馈进行再次优化迭代.学生在了解日常购物中平台商品搜索排序机理的同时，也能激发其探索机器学习背后微分方程求解机理的兴趣.

基于我国经济的飞速发展，教师可以向学生介绍我国风靡世界的新四大发明，即高铁、网购、移动支付和共享单车.新四大发明是中国科技创新的集中体现，极大地改变了人们的生活方式，也令外国友人对中国便利的日常生活羡慕不已.随着线上支付线上购物走入千家万户，教师可以向学生介绍我国在商品推荐、移动支付中取得的成就，以此坚定学生为国家发展奋斗的决心.

(三)天气预报与高性能计算、偏微分方程

近年来，随着地球温度的上升，极端天气出现的概率大幅增加.因此，天气预报在人们日常工作生活中扮演着越来越重要的角色.而学生在日常生活中发现，现在手机上的天气预报已经精确到以小时为单位，而且24小时内晴雨预报准确率高达88%.

教师在讲授完常微分方程以及偏导数之后，可以向学生介绍如下的方程形式：

设u=u(x,y,z)为二阶可微函数，则下列方程

uxx+uyy+uzz=0

该方程称为拉普拉斯方程.

通过引导学生将该方程与常微分方程进行对比，教师可以引出偏微分方程的概念，并介绍偏微分方程的几个应用场景.如手机上每日推送的天气预报，气象局会观测海上或者远处上空的气团，通过求解关于气团加速度和边界条件的偏微分方程来预测气团到达城市上空的时间以及强度，再结合当地的气象数据分析预测天气.学生对天气预报背后方程组求解问题的研究，不仅能回答自己日常生活遇到的问题，还能拓宽知识的广度，为后续课程学习打下基础.

此外，教师还可以介绍高性能计算机助力提高天气预报准确率的例子.如2021年7月，首夺世界第一的我国天河E级超级计算机利用数值计算高效求解了偏微分方程组，极大地提升了天气预报的效率和准确度.这对国家提供极端天气预警来避免人员伤亡和财产损失有着重大意义.学生也能从中感受我国在高性能计算这一领域的非凡成就，砥砺自身家国情怀.

(四)高铁速度与曲率

学习导数的应用-曲率这一部分内容时，曲率的公式推导相对较为抽象，而且公式不易记忆，学生对这一部分知识理解往往不够深刻.老师在上课时可以提出如下问题：“高铁凭借其方便、舒适、快捷、准点的特点，已经成为当今社会出行必备选择之一.高铁设计时速最高可达380 km/h，那么在行进到弯道、横风区域时，如何保证列车的安全平稳行驶是科研人员必须要考虑的问题.在高铁行驶过程中，有时即使在不经过站点的情况下，高铁的速度也会变化，在部分路段还会减速行驶，这背后有什么数学原理呢？具体来看，设计时速为380 km/h的路段需要考虑哪些相应的指标？”

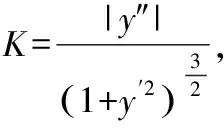
此外，教师可以向学生介绍我国高铁的发展历程、先进的高铁技术和便捷的铁路线上购票平台.其中高铁研发通过自主创新，在技术路线上实现了从全面模仿到领跑全球的骄人成绩.而铁路线上购票平台通过与具有自主知识产权的阿里云计算平台合作，在各大节假日购票高峰期多次经受住了考验.学生可以从中感受我国在相关技术领域的进步和积淀，激发其为国家奋斗的决心.

三、高等数学课堂实践效果

通过在课堂中逐步引入高等数学在热点技术中的应用典例，并将课程思政融入课堂教学，笔者主讲教学班的2020级自动化专业学生一学年来的学习效果较之前有了明显改善，具体数据如下图所示：

图1

从学生的学习热情度来看，经过一年的课堂实践，学生积极参与、愿意参与、消极参与的人数从21人、35人、15人转变为34人、31人、6人，变化明显.更多的学生积极地在课堂和线上学习平台提问、讨论交流，针对教科书上的定理证明和习题解法提出更多、更新的思路.积极查阅知识点相关资料，讨论高等数学在各个领域如无人机姿态保持、飞行路径选取、汽车导航优化等方面的应用.

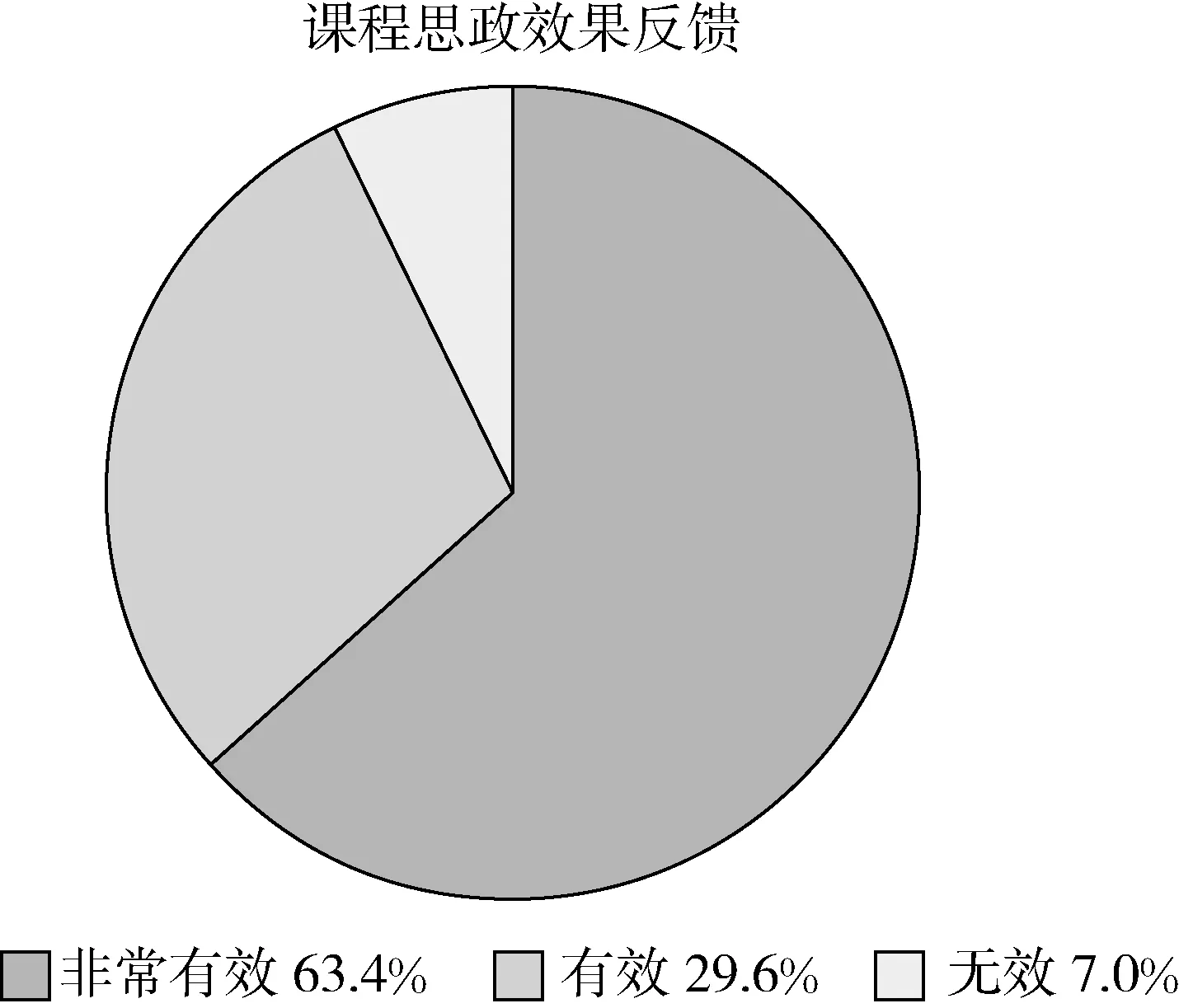
图2

从学生的德育效果来看，将课程思政融入课堂教学，学生反馈非常有效、有效和无效的比例分别为63.4%、29.6%和7%.学生开始关注国家在新兴技术领域(如区块链应用、基于大数据的消费行为分析等)上取得的成就，愿意未来投身相关行业并为国家在该领域的发展奉献力量.因此，在高等数学课堂教学中引入热点技术的应用典例并融入课程思政元素，能极大地激发学生的学习兴趣，提升其自主学习能力，也起到了很好的教学德育效果.

总之，根据新时代学生信息获取渠道广泛、紧跟热点的这一特点，有针对性地讲解新兴热点技术领域背后的高等数学知识，引导学生思考其中的数学问题,不仅能激发学生的学习热情、训练学生的逻辑思维和独立思考能力，还能将课程思政融入教学中，通过讲解高等数学是如何服务技术进步、国家发展的，帮助学生树立正确价值观，培养浓厚家国情怀，鼓舞学生为国家而奋斗终生.