基于鬣狗算法神经网络反演林地叶面积指数*

冷欣， 洪增宇

东北林业大学 机电工程学院， 哈尔滨 150040

叶面积指数(leaf area index， LAI)通常被定义为单位面积内所含的植被叶片表面积之和， 是植被重要的生物物理变化和结构参数[1]， 在农业、 林业领域应用广泛， 同时在生态系统与作物生长模型构建、 农业环境监测中具有重要研究意义[2].

凋落物法、 光学仪器法、 破坏取样法等LAI实地测量方法的测定值相对准确， 但费时费力， 难以获得大区域LAI值. 相较于实地测量， 利用遥感技术反演LAI具有覆盖范围广、 节约人力物力、 监测时间长等一系列优点， 可实现对区域尺度植被动态变化的快速获取和分析[3]， 是遥感技术的一项重要应用， 也是农林业遥感研究的重要内容之一[4]. 反演方法上， 主要有统计模型法和物理模型反演法. 统计模型法中最广泛使用的有植被指数法， 通过建立各种植被指数与实测LAI值的回归模型进行LAI反演， 这种方法简单便捷， 但机理性弱， 容易受地域反演植被类型等客观条件影响， 普适性较差[5]； 物理模型法基于物理模型， 通过建立LAI值与一系列基本参数和冠层反射率的关系实现LAI的反演， 这种方法机理性强， 普适性好， 不受作物类型和区域限制， 但是模型结构复杂， 需要输入较多参数[6].

随着遥感技术对非线性物理模型的优化要求越来越高， 而神经网络对非线性模型的拟合和模式识别方面有巨大优势， 于是逐渐成为利用遥感技术反演LAI方法中的一种常用方法. 由于神经网络存在局部极值和网络算法收敛速度慢等不足[7]， 为了弥补这些缺陷， 国内外众多研究者针对神经网络在LAI反演的应用上提出了很多的优化算法. 王枭轩等[8]基于高分一号影像利用粒子群神经网络反演玉米小麦LAI值， 并验证了该方法有一定的普适性； 薛华柱等[9]利用模拟退火算法的BP神经网络对农作物、 草地和林地等3种典型地表植被LAI进行反演， 验证了模拟退火算法可提高BP神经网络模型泛化能力； 陈士城等[10]利用BP神经网络和植被冠层辐射传输模型PROSAIL混合模型对农作物LAI进行反演， 取得了较好的反演结果； 谭德宏等[11]基于Sentinel-2多光谱影像利用遗传算法优化BP神经网络对高山松LAI进行反演， 为低纬度高海拔地区森林LAI研究提供了参考.

鬣狗算法是印度学者Gaurav Dhiman与Vijay Kumar于2017年提出的一种新的群智能优化算法， 具有参数少、 原理简单、 易于实现等优点， 有较好的全局搜索能力和收敛速度[12]. 本文基于高分一号卫星遥感影像和PROSAIL辐射传输模型反演数据， 建立了BP神经网络模型和鬣狗算法神经网络模型， 比较分析了两种模型的精度.

1 研究区域和数据

1.1 研究区域概况

本研究选取位于黑龙江省尚志市帽儿山地区部分林区作为研究区域. 帽儿山实验林场位于东经127°30′-127°34， 北纬 45°20′-45°25′， 属长白山系张广才岭西部小岭余脉， 植被属长白植物区系， 是东北东部山区较典型的天然次生林区， 植被类型属温带针阔叶混交林， 地带性顶极群落为阔叶红松林， 本地区土壤多为典型暗棕色森林土， 主要树种为红松、 落叶松、 樟子松、 水曲柳、 胡桃楸、 黄波椤、 椴树、 榆树、 白桦、 蒙古栎等[13-14]. 研究区域位置见图1.

审图号： GS(2019)3333号.图1 研究区域位置

1.2 数据获取与处理

1.2.1 遥感影像

本研究采用研究区域2018年6月17日GF-1 WFV影像数据作为研究数据. GF-1卫星装载4台多光谱宽幅相机， 运行在645 km高度的太阳同步轨道， 宽幅相机幅宽大于830 km[15]， 遥感影像为16 m分辨率， 4波段数据， 其基本参数如表1所示， 可作为林地LAI反演数据源[16].

表1 GF-1 WFV数据参数

1.2.2 数据预处理

遥感数据预处理包括辐射校正和大气校正. 利用ENVI5.3软件的Radiometric Calibration模块和Flaash先后对遥感数据进行辐射校正和大气校正[17]， 辐射校正采用绝对辐射定标方法， 大气校正采用Flaash模型， 所需的绝对辐射定标系数和波谱响应函数可在中国资源卫星应用中心下载获得. 为了避免少量云及其产生的阴影对实验产生干扰， 需要将此类像元剔除以达到清洗数据的目的， 由于大部分云的反射率在GF-1 WFV的4个波段中均大于0.1， 而云影的反射率很低甚至出现负值， 因此可将此类像元作为异常值进行剔除[18]. 影像中少部分人工建筑水体等像元可作为噪声保留， 以增强神经网络抗噪声能力， 减轻网络过拟合现象. 道路、 建筑密集的像元不作为研究对象， 也一并剔除， 图像处理结果见图2.

1.2.3 植被指数提取

植被指数是指根据植被光谱特性， 将卫星遥感影像中可见光和近红外波段反射率进行组合， 可对地表植被状况进行简单有效度量的指数. 本研究选取常用的6个植被指数(RVI，NDVI，SAVI，DVI，ARVI，EVI)， 分别记为RVI，NDVI，SAVI，DVI，ARVI，EVI. 计算公式如下：

(1)

(2)

(3)

DVI=ρnir-ρred

(4)

(5)

(6)

其中：ρnir，ρred和ρblue分别为大气校正后的近红外、 红外及蓝光的地表反射率，L为土壤调节系数， 本研究取L为0.5.

图2 标准假彩色遥感图像

2 实验方法

2.1 PROSAIL模型

PROSAIL辐射传输模型是PROSPECT模型和SAIL模型的融合， 综合考虑叶片生化参数、 植被冠层结构、 二向散射特性等， 被广泛应用于植被LAI参数反演[19]. 本研究使用Python环境下的PROSAIL第三方库， 该版本PROSAIL模型是由PROSPECT-5模型[20]和4SAIL模型[21]耦合而成. 模型所需生化参数和结构参数N可由LOPEX93植物生化参数数据库获取. 由于研究区域树木种类繁多且分布不均， 以及部分树种生化参数未能被数据库收录， 因此尽可能选择主要树种或主要树种的同属植物生化参数作为模型输入参数， 生化参数如表2所示.

表2 植物生化参数

模型运行结果为特定LAI值的反射率曲线， 如图3所示. 将LAI值从0～10以0.01为步长输入模型， 获得不同LAI值和各波段反射率对应的数据组合， 建立LAI-反射率查找表， 部分查找表见表3. 遍历影像每一像元， 基于像元各波段发射率和LAI—反射率查找表， 获得该像元的LAI反演结果， 研究区域反演结果如图4所示.

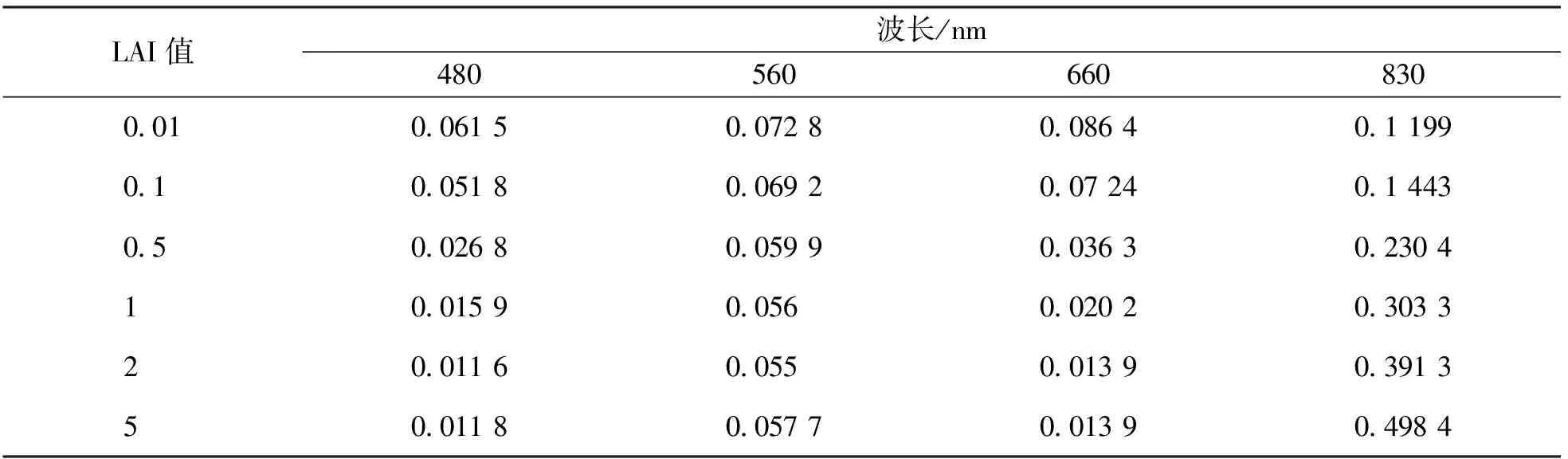
表3 LAI-反射率查找表

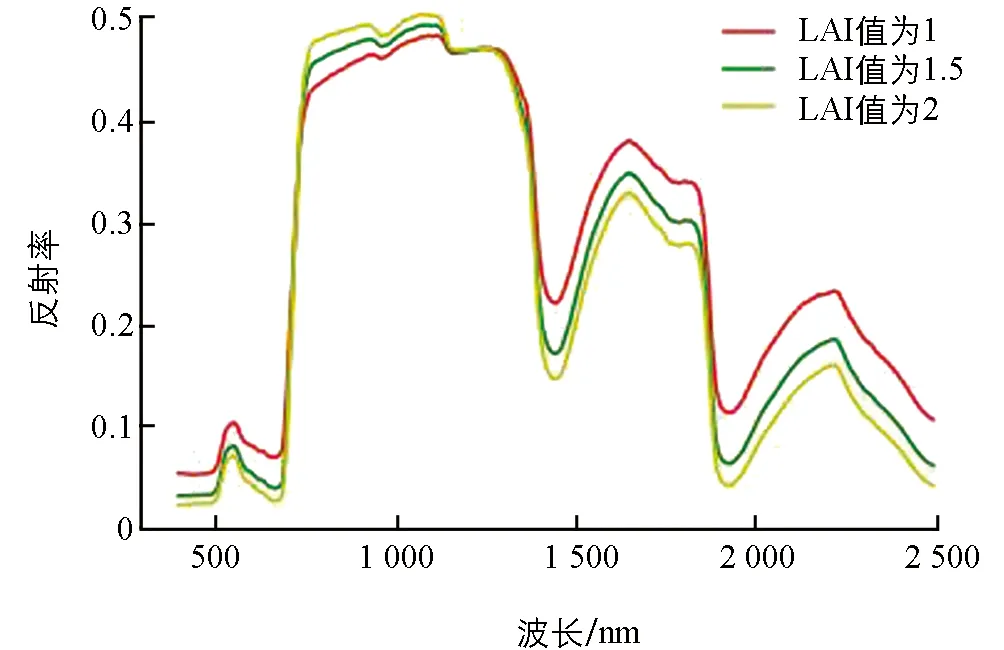
图3 反射率曲线

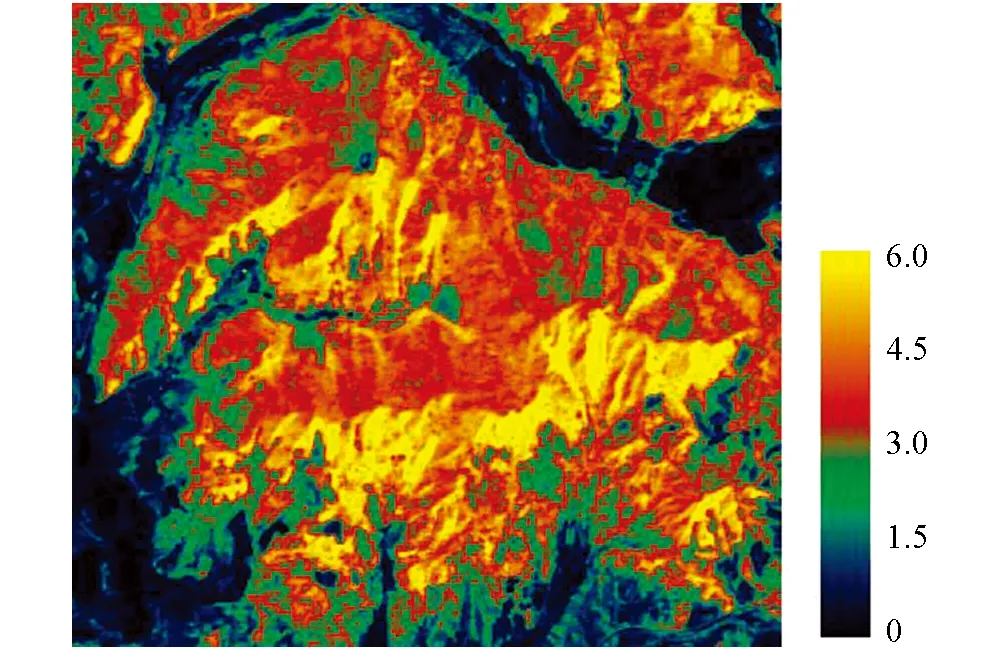
图4 LAI反演结果

图5 BP神经网络结构图

2.2 BP神经网络模型

BP神经网络模型是人工神经网络中应用最为广泛、 最具有代表性的神经网络模型， 比传统前馈神经网络在非线性映射能力上， 具有容错性强、 适应性强等优势， 结构如图5所示.

BP神经网络由输入层、 隐含层、 输出层三部分组成， 同层神经元平行无连接， 相邻层神经元由权重系数相互连接. BP算法通过信号的前向传播和误差的反向传播两个过程， 利用梯度下降法使网络的实际输出值和期望输出值的误差函数达到最小. BP神经网络前向传播过程、 隐含层神经元、 输出层神经元节点信号输入与输出关系为

(7)

Yi=f(N(i))

(8)

式中：XJ为信号输入，Wij为该神经元节点权值，μ为偏置值，f为激励函数，Yi为信号输出. 误差反向传播过程， 各神经元节点权值更新采用梯度下降法， 可选均方根误差(RMSE)作为误差函数：

(9)

Wij=Wij-δE(Wij)

(10)

式中：E为误差公式，E(Wij)为权值误差偏导，O为实际输出值，I为期望输出值， 权值不断更新， 直到误差函数为零或小于一定阀值.

2.3 鬣狗算法

鬣狗算法(Spotted Hyena Optimizer， SHO)是一种受启发于鬣狗种群觅食机制， 通过模拟鬣狗种群捕食行为以达到优化搜索的新型群智能优化算法. SHO算法操作简单、 设置参数少、 稳定性强、 求解精度更高， 因其性能良好， 已经开始被应用于解决非线性连续优化问题等多个工程领域[22].

鬣狗算法包括搜索、 包围、 狩猎和攻击猎物的4个过程， 以求在全局和局部搜索到最优点[23]. 鬣狗算法的基本原理如下：

1) 包围机制： 鬣狗群搜寻猎物的位置， 并尝试向猎物靠近， 该行为的数学模型为

Dh=|B·Pp(t)-P(t)|

(11)

B=2·r1

(12)

式中：Dh表示鬣狗个体与猎物之间的距离；t表示当前迭代次数；Pp表示猎物的位置；P(t)表示鬣狗种群中的个体位置；B表示摇摆因子；r1表示[0， 1]之间均匀分布的随机数.

鬣狗的个体位置更新可表示为

P(t+1)=Pp(t)-E·Dh

(13)

E=2·h·r2-h

(14)

(15)

式中：E为收敛因子，r2表示[0， 1]之间均匀分布的随机数，h表示控制因子，t表示算法当前的迭代数目；T表示最大迭代次数.

2) 狩猎机制： 鬣狗群通过可靠的种群网络， 迅速向距离猎物最近的最优个体靠拢， 并试图包围猎物， 该行为的数学模型为

Pk=Ph-E·Dh

(16)

Ch=Pk+Pk+1+…+Pk+N

(17)

式中：Ph定义了距离猎物最近的鬣狗的位置，Pk表示其他鬣狗的位置，N表示鬣狗数量，Ch是N个最优解的集群. 其中N计算式为

N=Count，nos(Ph，Ph+1， …， (Ph+M))

(18)

式中：M为[0.5， 1]的随机向量， nos为定义解的数量， 并计算所有候选解.

3) 攻击猎物： 在收敛因子|E|<1时， 鬣狗群选择攻击猎物， 离猎物最近的个体尝试向猎物靠近， 全局最优解更新为最优解集的平均值， 数学模型为

(19)

式中：Ph(t+1)为最优解，Ch为最优解集群，N为鬣狗数量.

4) 搜索机制； 在收敛因子|E|>1时， 鬣狗群选择不攻击猎物， 而是继续向猎物靠近， 搜索更合适的位置， 这使得SHO算法能够在全局进行搜索.

3 实验设计

3.1 BP神经网络模型构建与训练

由于BP神经网络隐含层的层数选取并没有可靠的理论指导， 隐含层过多会造成过拟合和收敛速度慢等问题， 因此根据奥卡姆剃刀原则和以往经验， 本研究中BP模型选择3层网络模型， 即输入层、 输出层以及隐含层. 输入层为10个神经元， 分别输入GF-1 WFV四波段反射率和6种植被指数； 输出层为1个神经元， 输出预测的LAI， PROSAIL模型反演得到的LAI值作为期望输出值， 选取均方根误差(RMSE)作为误差函数， 记为RMSE， 计算公式为

(20)

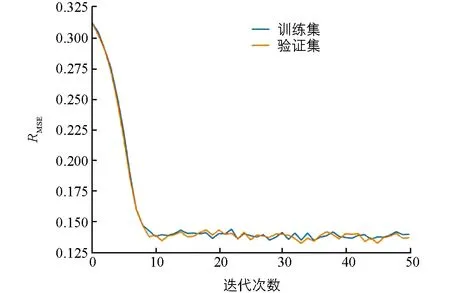
图6 BP神经网络训练收敛曲线

神经网络训练收敛曲线如图6所示， 网络训练集RMSE值为0.140， 验证数据集RMSE值为0.137， 权值阈值见表5.

表4 部分数据集

表5 BP神经网络权值阈值表

图7 鬣狗算法神经网流程图

3.2 基于鬣狗算法的神经网络模型的构建与训练

鬣狗算法可用于训练前馈神经网络， 将神经网络各个参数向量化为公式：

V={W11，W12， …Wij，θ1，θ2， …θj}

(21)

式中：Wij为从第i个隐藏层节点到第j个输出节点的连接权值，θj为第j个节点的偏置值， 向量V可作为鬣狗群的位置向量， 猎物位置向量即为神经网络最优连接参数. 将误差函数值作为鬣狗个体适应度值， 即表示为鬣狗个体与猎物的距离， 适应度值逐渐减少， 鬣狗靠近猎物， 网络参数靠近最优解. 算法流程如图7所示.

鬣狗神经网络结构与上述BP神经网络结构相同， 用鬣狗算法替换梯度下降法训练神经网络， 鬣狗种群数目设定为20， 实验运行环境为Python3.7.

网络训练收敛曲线如图8所示， 由图可知， 鬣狗神经网络在RMSE值为0.145和0.140时陷入局部最优并跳出， 最终训练集RMSE值为0.131， 验证数据集RMSE值为0.132， 权值阈值见表6. 部分迭代次数最优个体位置向量如图9所示， 其中维度0～49为输出层神经元到隐含层神经元权值， 维度50～55为隐含层神经元到输出层神经元权值， 维度56～60为隐含层神经元阈值， 维度61为输出层神经元阈值.

表6 鬣狗神经网络权值阈值表

图8 鬣狗神经网络训练收敛曲线

图9 最优个体位置向量

基于高分一号卫星遥感影像和PROSAIL辐射传输模型反演数据， 分别建立了BP神经网络模型和鬣狗算法神经网络模型， BP神经网络的训练数据集RMSE值为0.140， 验证数据集RMSE值为0.137， 测试集决定系数为0.525. 鬣狗神经网络的训练数据集RMSE值为0.131， 验证数据集RMSE值为0.132， 测试集决定系数为0.703， 验证结果如图10.

图10 验证结果

4 结论

由结果可见， 两种模型预测结果都略大于期望值， 但鬣狗算法神经网络可以跳出局部最优， 在LAI值大于3的数据中， 表现更良好， 且总体精度高于BP神经网络， 可提升神经网络模型的反演性能. 综上所述， 鬣狗算法在神经网络上的应用可为基于遥感技术反演LAI提供一种新的方法.