障碍函数法在状态约束混杂系统稳定性中的应用

李亮亮，姜文琳

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

近些年来，混杂微分系统作为一个非常活跃的研究方向，吸引一大批来自不同领域的学者进行研究［1-5］. 实际系统中必然要受到某些约束，例如状态约束、输出约束及执行器饱和等［4-6］. 约束现象受系统自身的物理属性、结构和材料等影响，包括延迟、死区、饱和等问题［7-9］，比如，在机器人控制中，由于电机控制的最大转矩导致执行器饱和，这可能导致机器人部分控制信号丢失，导致机器人偏离预定轨迹，发生安全事故. 如果在控制系统的设计中忽略这些非线性特性的影响，那么整个非线性系统可能会变得不稳定［9-11］. 因此，有必要研究带有约束的非线性系统的稳定性问题. 文献［12］考虑状态约束线性系统的非凸最优控制问题. Ngo 等［13］提出利用障碍Lyapunov 函数研究状态约束系统的反步设计控制问题. 文献［14］中利用障碍Lyapunov 函数考虑一类全状态约束系统的自适应控制问题，文献［15］解决一类带有执行器饱和的时滞动力网络的指数同步控制问题. 然而，尽管有不少文献都对约束问题进行深入的研究，但目前这些方法都不能直接处理状态约束脉冲非线性系统的稳定性问题［14，16-17］. 本文提出一种特殊的状态反馈控制器，利用矩阵理论和凸分析方法，分析闭环非线性动态系统的状态轨迹的稳定性问题，以解决带有脉冲扰动的状态约束动力系统的控制问题.

1 模型简介与理论基础

本文考虑如下一类混杂动力微分方程：

集合T0表示系统的不变集，对任意的x0∈T0，当t≥0, 始终有x(t,x0)∈T0. 下面给出一个混杂系统不变集的充分条件.

定理1 设D是Rn中的一个有界域，若对任意的正数μk≤1 和α，都存在一个正定函数V(t)≜V(x(t))满足：

注1 在定理1中，如果取μk=1 和α=0，定理显然也成立，可以作为推论在后面的理论分析中起到很关键的作用. 此结论可以分析比较著名的弹跳球系统或者小车碰撞模型问题，这些都是比较典型的约束混杂系统. 比如考虑如下模型，如图1 所示，假设这里x(t)表示球的高度，y(t)表示震荡平台的高度，e1(t)表示相对位移，e2(t)表示相对位移的速度，g表示重力加速度，m表示球的质量（相对于平台的质量忽略不计），假设只受重力的影响，所有的碰撞都是瞬间完成的，弹跳球模型建模如下

图1 弹跳球系统模型

根据定理1，可以得到球最终将停留在平台上面，和平台一起运动，图2是仿真的弹跳球系统运行轨迹.

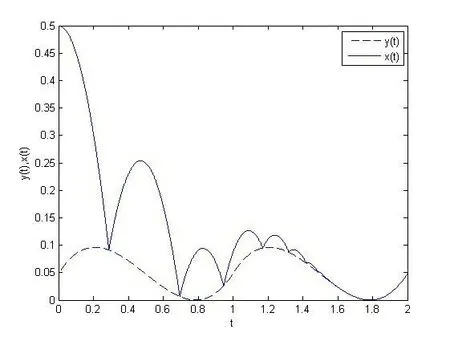
图2 系统（2）的状态轨迹

2 状态约束脉冲动力网络的控制设计

考虑如下一类耦合非线性动力网络的镇定问题

根据定理1，很容易得到系统（4）的状态始终停留在Θ中并且收敛到0，结论得证.

3 结论

文章主要考虑一类混杂状态受限的系统稳定性问题，利用不变集原理，数学归纳法，构造障碍Lyapunov 函数考虑脉冲复杂动力网络的控制问题，本文构造的障碍函数是一类对称的Lyapunov 函数，可解决一类对称约束问题，而非对称问题还需要进一步考虑，非对称的障碍函数的构造也是一个待解决的主要问题.