基于门控循环单元的全断面掘进机稳定段掘进性能预测
张弛, 李艳, 王鹏, 刘沛, 梁科森
(中南大学机电工程学院,长沙 410083)
随着综合国力的不断提升,中国正成为世界隧道工程技术发展最快的国家,全断面隧道掘进机(tunnel boring machine, TBM)产业规模和市场规模均已是全球首位[1]。全断面隧道掘进机施工法与钻爆法相比,具有开挖速度快、施工安全性高、隧道成型质量好、工程造价低的优点,在深长硬岩隧道中应用广泛[2-3]。安全和高效掘进是TBM施工中的两大主要目标,而开展TBM施工中的掘进性能预测是实现安全和高效掘进的基础。为此,中外学者进行了大量的研究,掘进性能预测方法主要包括基于模拟掘进实验的理论方法、经验公式方法和机器学习预测方法。
TBM掘进性能预测理论方法通过开展模拟掘进实验分析单个滚刀上的受力,进而计算出整个刀盘所需的总推进力、刀盘扭矩等参数[4-5]。模拟掘进实验通常可分为全尺寸实验和缩尺实验, Gertsch等[6]基于全尺寸盘形滚刀开展破岩实验,记录不同刀间距和贯入度下滚刀的三向力,分析滚刀参数和掘进参数的不同组合对掘进性能的影响;Ma等[7]通过开展缩尺掘进实验分析了围压对盘形滚刀法向力、滚动力、切削系数和比能的影响;Yin等[8]通过开展全尺寸线性破岩实验分析了节理间距等参数对岩石破碎性能的影响。
经验公式方法通常采用线性或非线性方法来建立TBM掘进性能预测模型,这种模型通常以岩体力学参数作为输入变量,预测TBM掘进参数。王健等[9]采用岩体质量分级(rock mass rating, RMR)系统建立了掘进速率、施工进度、利用率和场切深指数(field penetration index, FPI)的经验公式,并基于吉林引松工程数据验证了模型的预测效果;Yagiz等[10]利用RMR系统来预测TBM利用率的研究,发现TBM利用率与RMR存在着一定的相关性,且这种相关性由岩体参数和TBM设计参数共同决定。
由于不同隧道的地质存在差异、岩体力学参数稀缺等原因,理论和经验公式方法有很大的局限性。随着人工智能技术的快速发展,近年来,越来越多的研究人员开始采用机器学习方法进行TBM掘进性能预测研究。赵光祖等[11]利用模拟退火算法和遗传算法对BP(back propagation)神经网络进行优化,进而用于TBM掘进性能预测,得到了较传统BP神经网络更好的预测效果;周小雄等[12]为预测TBM稳定段性能参数,提出了一种融合注意力机制的双向长短时记忆神经网络,实现了对稳定掘进段推力和扭矩的预测;侯少康等[13]提出了一种利用改进粒子群算法优化BP神经网络的预测模型,实现了对TBM稳定段掘进参数的预测。朱梦琦等[14]采用基于集成分类与回归树(classification and regression trees, CART)算法的AdaCost实现了对TBM稳定掘进时的掘进参数预测。谢士平[15]利用改进的BP神经网络进行了超特长隧洞TBM掘进速度的预测;Liu等[16]利用BP神经网络集成模拟退火算法,实现对围岩参数的预测。Adoko等[17]以岩石类型、单轴抗拉强度等岩体参数并结合总推进力作为输入特征,基于模糊推理系统建立了FPI预测模型。
综上所述,目前的TBM掘进性能预测研究主要是运用TBM结构设计参数、岩体参数等数据开展研究,对掘进循环不同的阶段变化考虑不足。同时由于不同工程的施工设备和作业地质环境差异明显,因此存在较大的场地特异性和局限性。鉴于此,依托新疆某供水工程,基于大量TBM掘进数据,充分考虑了各掘进参数及围岩情况对掘进性能参数的影响,借助门控循环单元(gated recurrent unit, GRU)神经网络构建TBM掘进性能预测模型,为实现TBM安全高效掘进提供参考和借鉴。
1 施工数据分析与预处理
1.1 工程概况
工程数据源自新疆某引水工程Ⅱ标段,采用1台国产敞开式TBM施工,标段总长约25 km。从Ⅱ标段TBM信息存储系统中提取约750天的施工数据,依据围岩等级进行数据量统计,如图1所示。该标段地质岩性主要为凝灰岩及凝灰角砾岩,Ⅱ~Ⅴ类围岩占比分别为54.24%、8.17%、24.74%、6.16%和6.68%,以Ⅱ类和Ⅲ类围岩居多,各类围岩等级下数据丰富,围岩地质环境总体较好,为之后的研究提供了良好的数据基础。
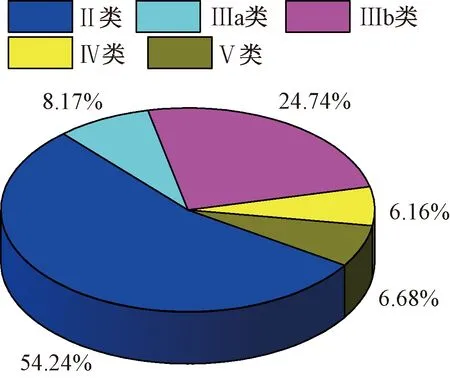
图1 围岩类别占比
1.2 数据预处理
由于TBM的施工特点,数据系统中储存了大量停机、换刀、围岩支护、设备维修等非工作状态数据,对掘进性能预测没有太大价值,因此采用王超[18]提出的二值状态判别法剔除非工作状态数据。
剔除掉非工作状态数据后,由于传感器故障、操作失误等原因,TBM 工作状态数据中还存在多种类型的异常值。观察发现,这些异常值以极大值为主且呈现脉冲特性,通常出现在推进速度这一掘进参数中,如图2所示。
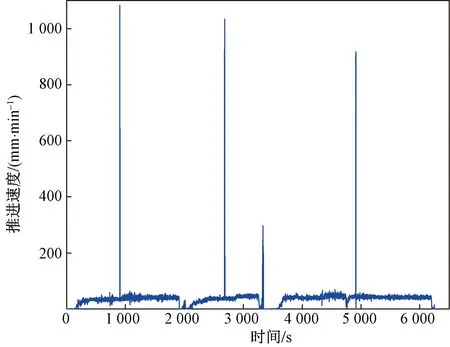
图2 某个时间段中推进速度极大值异常点

表1 推进速度参数
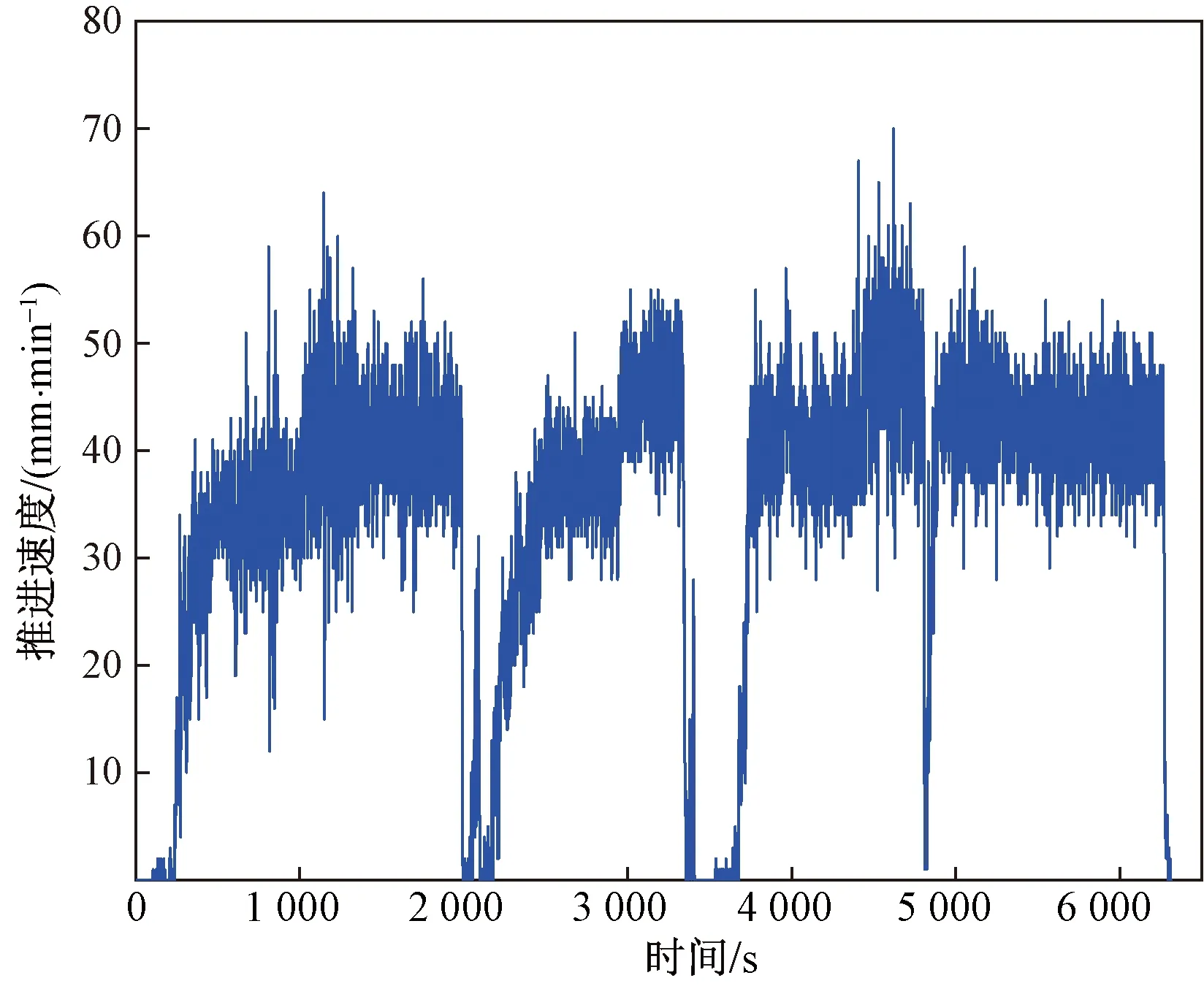
图3 剔除异常值后TBM施工片段
1.3 掘进循环划分
由于敞开式TBM的独特结构,其掘进过程具有典型的步进式特征(即掘进循环)。一个掘进循环内TBM各掘进参数变化趋势可分为空推段、上升段和稳定段3个阶段[19],如图4所示。①空推段:从TBM启动到刀盘与掌子面接触;②上升段:滚刀接触岩石,推进力、扭矩等掘进参数快速增大,直至刀盘完全贯入岩体;③稳定段:TBM各掘进参数保持稳定直到循环结束。研究TBM上升段掘进参数是保障稳定掘进的前提,通过掘进循环上升段参数来预测稳定段TBM掘进性能,为驾驶员设定稳定段的掘进参数提供借鉴和指导,进而实现安全高效掘进。
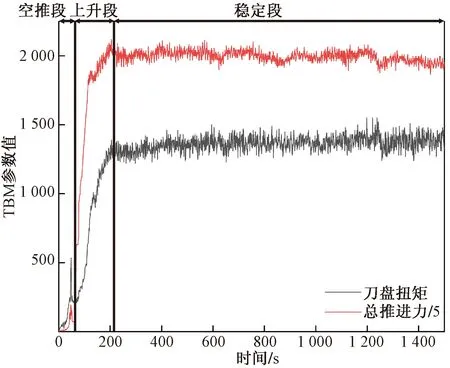
图4 TBM单个掘进循环的阶段划分
2 稳定段掘进性能预测模型构建
2.1 算法原理
预测模型的输入输出均为时间序列数据,循环神经网络(recurrent neural network, RNN)在处理时间序列时具有明显优势,然而由于梯度消失和梯度爆炸问题的存在,使得RNN神经网络处理长时间序列数据的能力不足。GRU神经网络是对传统RNN的改进,通过改变神经元的内部结构,解决了梯度消失问题,由于内部结构简单、超参数少、训练快速的特点,实现了对长时序列的有效处理,基本结构单元如图5所示,其数学描述为
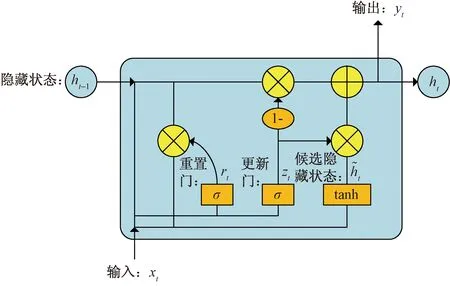
图5 GRU结构示意图
(1)
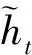
2.2 输出输入特征选择
上升段和稳定段为岩-机相互作用的阶段,驾驶员通常根据上升段掘进参数的数值变化,依据施工经验判断TBM工作状态,调整稳定段掘进参数。其中,总推进力和刀盘扭矩是驾驶员判断TBM工作状态的主要运行参数,是设定TBM控制参数的重要依据[19]。因此,选取总推进力和刀盘扭矩作为预测模型的输出参数,由此预测TBM稳定段掘进性能。
掘进过程中TBM上传感器记录的掘进参数种类繁多,从这些掘进参数中选择最优的参数对降低预测模型复杂度,提高预测精度有十分重要的意义。采用过滤法(特征相关性分析)从多参数中选取最优输入特征,对工程Ⅱ标段的掘进参数进行相关性分析,部分掘进参数之间的相关性热力图如图6 所示。
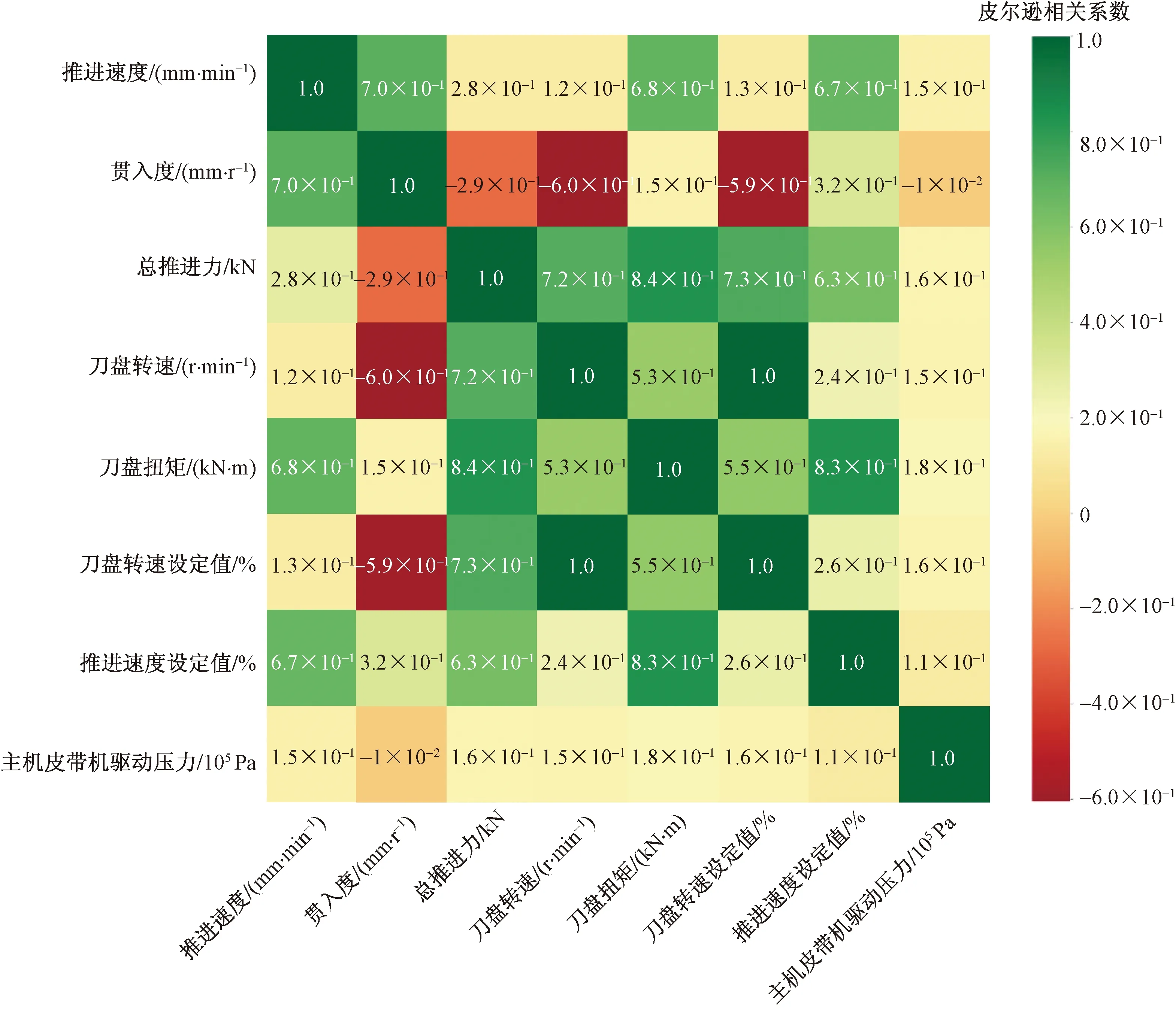
图6 部分掘进参数相关性热力图
由图6可知,与总推进力相关性较高的掘进参数为:刀盘扭矩(0.84)、刀盘转速设定值(0.73)、刀盘转速(0.72)、推进速度设定值(0.63)、推进速度(0.28);与刀盘扭矩相关性较高的掘进参数为:总推进力(0.84)、推进速度设定值(0.83)、推进速度(0.68)、刀盘转速设定值(0.55)、刀盘转速(0.53)。参数A与参数B之间的相关性越高,说明参数A对参数B的依赖程度越强,在模型中能提供的新信息就越少。部分相关性较强的输入参数如表2所示,在预测模型构建时,相关性较强的参数取其中一个作为输入。

表2 部分相关性较强的输入参数组合
根据过滤法所得结果,选取刀盘扭矩、总推进力、刀盘转速、推进速度为模型的输入特征组合。另外,基于随机森林(random forest, RF)特征重要性排序[20]及工程经验,选取贯入度为输入特征。
围岩等级也会对掘进参数产生较大影响,如图7所示。依据工程地勘实测数据,将围岩等级信息与掘进参数进行对应,以One-Hot编码的形式作为模型输入。某个样本中输入参数如表3所示。
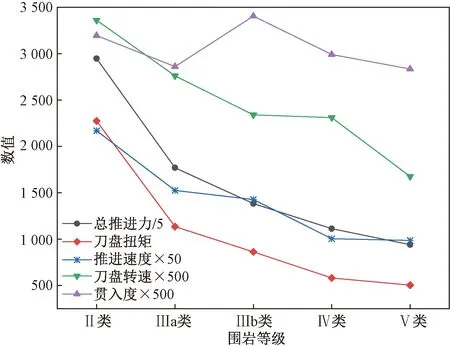
图7 不同围岩等级下TBM主要掘进参数均值对比
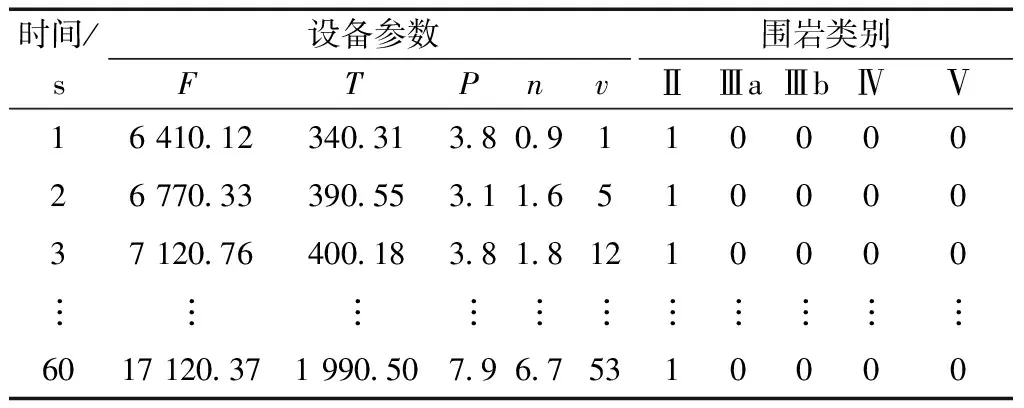
表3 某个样本中输入输出参数数值
2.3 模型结构及评价指标
神经网络结构、超参数的设置均会对模型的性能产生很大影响。经多次试验调优,最终确定模型采用三层隐藏层结构,每层包含60个神经元,设置训练次数epochs为100次,批量大小batch_size为100,学习率lr为0.001。参考目前的普遍研究基础,选用均方误差(mean square error,MSE)和Adam作为编译模型时的损失函数和优化器
为了量化模型预测误差,选择拟合优度R2和平均绝对百分比误差(mean absolute percentage error,MAPE)两个评价指标,计算公式分别为
(2)
(3)
式中:yai为实际值;ypi为预测值;i为样本号;n为测试集总数。
3 结果分析与讨论
将提取出的2 715个掘进循环数据,按9∶1的比例划分训练集(共2 444个循环)与测试集(共271个样本),输入预测模型,验证GRU神经网络模型预测效果,并与传统RNN模型预测结果进行对比分析。
3.1 GRU与RNN模型预测精度对比
以掘进循环上升段前60 s的数据作为输入,采用相同的结构和参数分别建立GRU及RNN掘进载荷预测模型,对掘进循环稳定段的总推进力和刀盘扭矩均值进行预测,结果如图8所示。可以看出:GRU模型得益于门机制的使用,因此对总推进力和刀盘扭矩的预测吻合度较RNN模型均有所提高,且预测偏差大的样本数较少,同时并未增加过多的模型训练时间。另外,由于刀盘扭矩为受多参数影响的被动量,具有更大的不确定性,因此两模型对总推进力的预测拟合度均比刀盘扭矩要高。

图8 两种模型预测结果对比
两模型的预测评价指标结果如表4所示。可以看出:GRU模型对总推进力预测的拟合优度R2为0.929,对刀盘扭矩的拟合优度R2为0.909,均在0.9以上;对掘进参数的预测平均绝对百分比误差MAPE都低于RNN模型且均在12.25%以内。总体来说,GRU模型的预测精度要优于RNN模型。
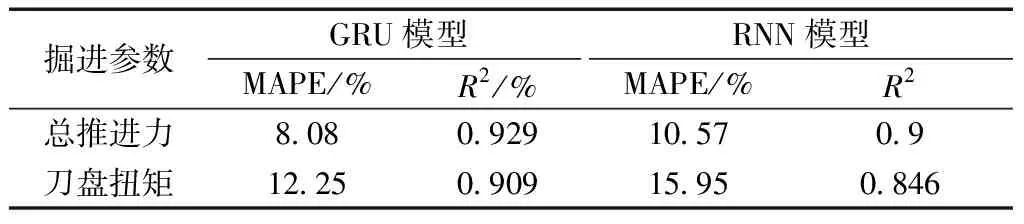
表4 不同模型预测精度对比
3.2 模型对不同长度时序输入适应能力
为进一步验证所设计的GRU模型能够准确预测稳定段掘进性能,选取不同时长的上升段数据作为输入变量进行预测。以上升段开始为起点,分别取上升段前30 s、前60 s、前90 s的数据作为模型输入,对比分析不同长度时序输入下模型的预测精度。
在Ryzen7 3700X处理器上前30 s、前60 s、前90 s输入的模型训练时长分别为:5、9、16 min,预测精度如图9所示。可以看出:不同时序长度输入情况下,总推进力和刀盘扭矩的预测精度变化不大且均较好,两个掘进参数拟合优度R2均在0.867以上,平均绝对百分比误差MAPE均小于13.84%。总体来说,所用GRU模型在应对不同长度时序输入时,均能保持较高的预测精度,模型泛化力较强。
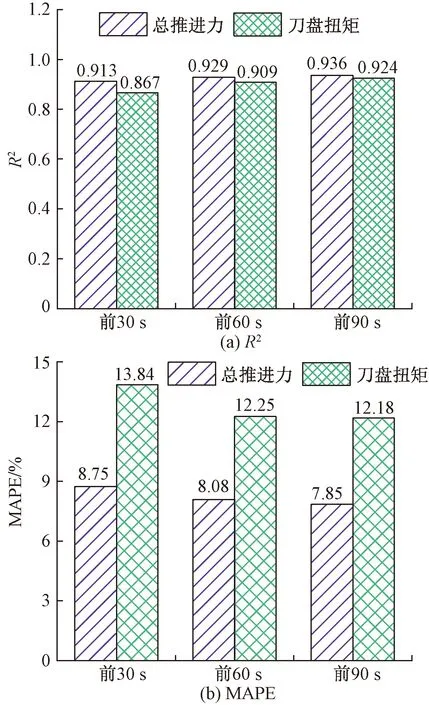
图9 不同上升段时间序列输入的预测精度对比
4 结论
依托新疆某供水工程TBM原始掘进数据,选用总推进力、刀盘扭矩、刀盘转速、推进速度和贯入度5个参数作为预测模型输入特征,并将围岩等级以One-Hot形式作为地质参数输入,建立了TBM稳定段掘进性能预测模型,实现对稳定段总推进力和刀盘扭矩的预测。得出如下主要结论。
(1)以上升段TBM各掘进参数和围岩等级作为输入参数,分别构建GRU和RNN神经网络模型,对比分析两种预测模型对稳定段总推进力F和刀盘扭矩T均值的预测精度。结果表明:GRU神经网络模型对两个掘进参数的预测拟合优度R2均在0.9以上,平均绝对百分比误差MAPE均小于12.25%,较RNN模型的预测精度更高。
(2)在应对不同长度时序(上升段前30 s、前 60 s、前90 s)输入时,GRU模型均能保持较高的预测精度,模型的灵活性和泛化力较好。

