煤柱-充填体联合控制地表变形规律研究

郭亚奔，张 晓,2,3，史久林,2,3，李 立,2,3，胡 滨,2,3，顾士超

(1.天地(榆林)开采工程技术有限公司，陕西 榆林 719000；2.煤炭科学研究总院开采研究分院，北京 100013；3.天地科技股份有限公司，北京 100013)

随着城市建设发展和煤炭资源开采强度增大，“三下”压煤问题愈发严重，据不完全统计，我国面临的“三下”压煤量约为137.9亿t，其中，建筑物下压煤量达到约为87.6亿t[1-2]。建筑物下压煤问题严重影响矿区的正常生产和接续，针对此问题，相关学者从留设保护煤柱、条带开采和充填开采等方面展开研究[3-5]。常西坤[6]利用极限理论和AH威尔逊煤柱强度理论综合分析确定葛亭煤矿230采区村庄下煤柱留设45 m时，可保证安全生产，但回采率仅为47.1%；李金贵[7]对建筑物下煤柱留设进行模拟，确定煤柱不小于130 m时可保证矿井安全生产；郭振兴等[8]通过理论分析和数值模拟，确定在采宽20 m条件下保护煤柱的合理宽度为20～26 m；周泽等[9]研究发现采用垂线法留设50 m保护煤柱以及合理开采措施可有效控制地表变形；刘义新等[10]提出了巷柱式联合加固留设煤柱条带开采技术，采宽100 m，留宽100 m，采出率由40%提高到50%；董羽等[11]通过理论分析得出当条带开采村庄下压煤时，留设煤柱宽度60 m，可使地表保持长期稳定；杨伟峰等[12]采用采宽30 m、留宽40 m的条带开采方式对建筑物下进行开采，各项移动变形最大值均处在地表建(构)筑物保护等级Ⅰ级以内，不会引起建筑物破坏问题，但采出率仅为42.86%～50.00%；常庆粮[13]通过地表沉陷预计模型，预测小屯矿充填开采时地表下沉系数控制在0.16以内，可保证南旺村建筑物安全，但充填成本增加60.4元/t；李秀山等[14]采用矸石膏体充填开采建筑下压煤，实测地表最大下沉量仅为35 mm，远小于原设计预计的300～400 mm，控制效果良好；娄高中等[15]采用概率积分法预计分析超高水充填开采对建筑物的影响，结果表明，工作面推进270 m时，地表最大下沉值仅为43 mm，地表村庄建筑物损害级别控制在地表建(构)筑物保护等级Ⅰ级以内。

留设保护煤柱、条带开采和充填开采均可控制上覆岩层移动，留设保护煤柱和条带开采可很大程度保护地面建筑的安全，但采出率仅为30%～50%[16-17]，资源浪费严重；而利用充填体支承上覆岩层，则受材料性能、成本的制约[18-19]。因此，寻求煤柱和充填体的合理范围是非常有必要的，一方面可以减少煤炭资源的浪费，实现建筑物下煤炭资源的高效开采；另一方面可以降低充填材料成本，实现企业效益最大化。

1 工程背景

阿尔巴斯二矿位于内蒙古鄂尔多斯境内，井田面积10.47 km2，采用斜井多水平开拓方式。一水平开采9#煤层，井田北部9#煤层已开采至六采区，大范围采空；二水平开采16#煤层。矿井9#煤层平均厚度3.6 m，煤层倾角平均4.5°，煤层结构较复杂。矿井六采区CT6902工作面和CT6903工作面地面有鄂尔多斯电业局110 kV变电站、石料厂和多家牧民房屋等建(构)筑物，压煤约649.95万t，地面建(构)筑物严重影响煤炭资源的回采与矿井正常接续；而牧民生活区存在若干牧民房屋，房屋构造为砖混结构，对变形有不同响应，具体情况如图1所示。结合胶结充填首采工作面地质采矿条件和地面建(构)筑物分布情况，重点保护鄂尔多斯电业局110 kV变电站、石料场和多家牧民房屋等建(构)筑物，充填开采产生的采动影响程度均需控制在轻微损害范围内。

图1 地表建(构)筑物分布情况Fig.1 Distribution of surface building (structure)

2 联合控制方案对比分析

2.1 联合控制方案设计

联合控制方案设计了充实率为80%、85%、90%、95%，工作面采深为200 m，煤柱宽度为6 m、12 m、18 m、24 m时的地表变形方案，具体方案见表1。

表1 联合控制方案Table 1 Joint control scheme

2.2 充填开采地表变形研究方法

1) 概率积分法。根据采煤沉陷地表移动特征可知，矿井采煤引起的地表沉陷规律基本符合概率积分法地表沉陷预测模型，而充填开采地表沉陷预计则引入等价采高理论模型[20-21]。煤层采高可采用等价采高理论计算得出，因此，预设模型参数需对垮落法预计参数进行优化，选取适用于充填开采的地表沉陷预计参数。根据矿井地表变形实测结果分析，开采造成的地表沉陷规律基本符合概率积分法预测模型，其预计精度完全可以满足对矿井充填采区进行地表沉陷预计[22]。

根据现场对矿区沉陷地表移动参数调查并查阅资料，地表移动参数选取如下所述[23]。①对于9#煤层首采工作面CT6902，采用长壁逐巷胶结充填开采，参数选取为下沉系数q=0.7、水平移动系数b=0.3、主要影响角正切tanβ=2、拐点偏移距为0、开采影响传播角为87.5°。②对于9#煤层全部胶结充填开采之后，考虑重复采动影响，参数选取为下沉系数q=0.87；水平移动系数b=0.3；主要影响角正切tanβ=2.16；拐点偏移距为0；开采影响传播角为87.5°。

2) 三维数值模拟分析。采用FLAC3D数值模拟软件对首采充填区域充实率以及工作面保护煤柱进行数值模拟，根据工作面宽度建立模型的长×宽×高为560 m×476 m×250 m。工作面推进长度为480 m，每个工作面宽度190 m，模型边界分别留宽40 m的边界煤柱，模型建至地表，具体参数见表2，模型网格划分如图2所示。

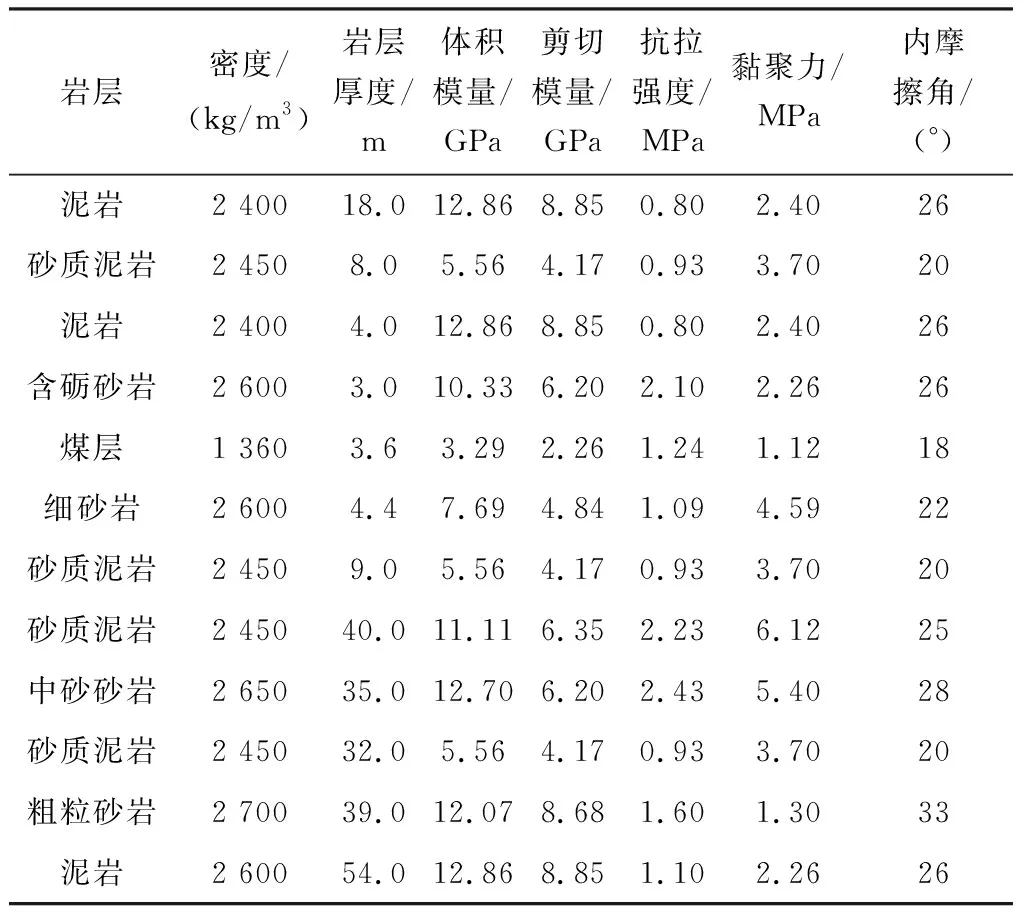
表2 岩体的物理力学参数Table 2 Physical mechanics parameters of rock mass

图2 模型网格划分图Fig.2 Model grid division diagram

3 充填开采地表变形规律分析

3.1 概率积分法地表沉陷预计

根据矿井首采区域煤层实际地质条件，煤层采高厚度为3.6 m，将选取的地表沉陷预计参数代入基于等价采高的概率积分法地表沉陷预测模型，沉陷预计结果见表3。

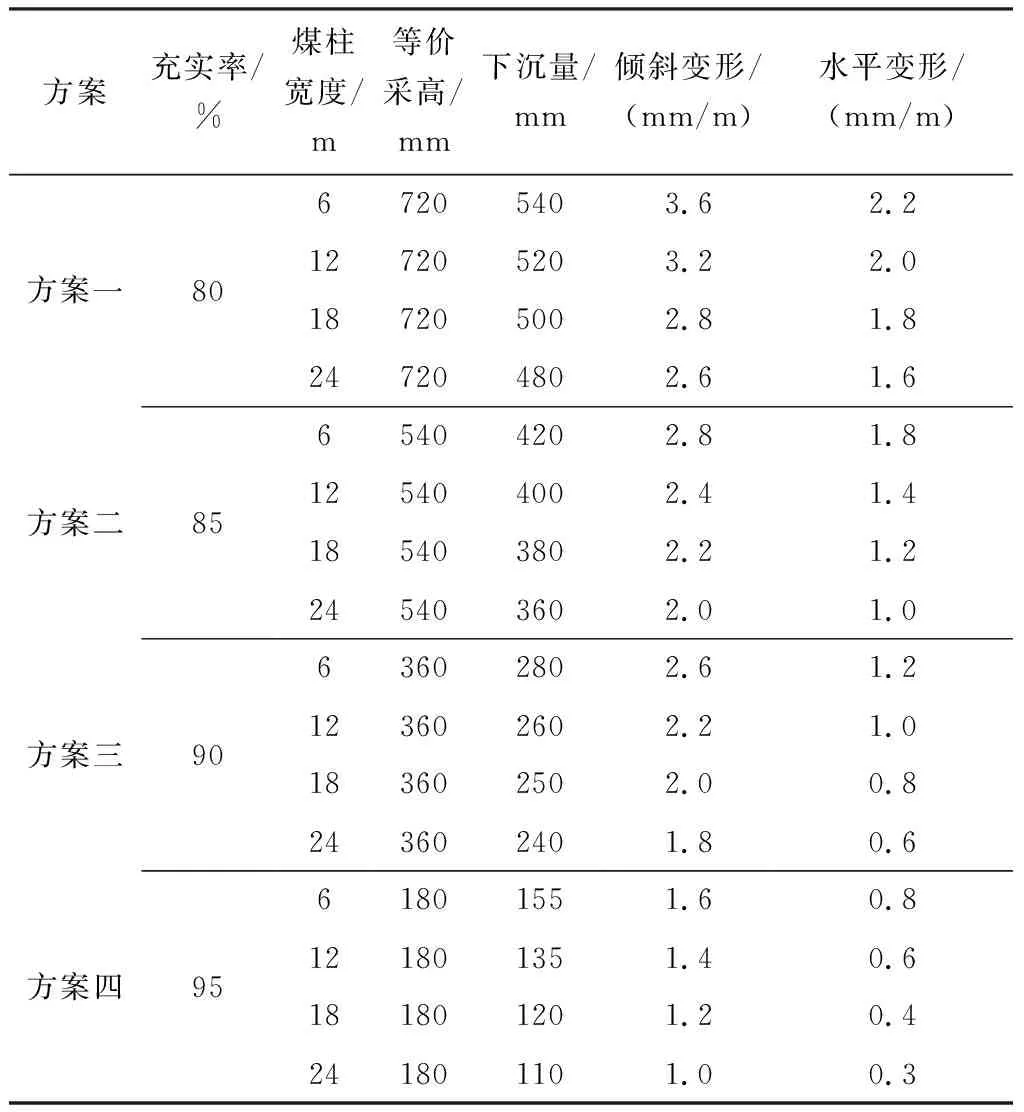
表3 地表沉陷预计结果Table 3 Surface subsidence prediction results

由表3可知，充实率一定时，地表下沉量与保护煤柱宽度呈线性关系，地表下沉量随煤柱宽度的增大而减小，当充实率为85%，保护煤柱宽度从6 m增大至24 m，地表下沉幅度降低了14.29%；而煤柱宽度一定时，地表下沉与充实率呈线性相关，当保护煤柱为12 m时，充实率从80%提高至95%，地表下沉幅度降低了74.04%。将实验数据进行回归，得到地表下沉量与煤柱宽度的关系为Y=-3.33X+440，R2=1；地表下沉量与充实率的关系为Y=-25.9X+2 595，R2=0.99。

根据地表建(构)筑物保护等级确定等级为Ⅰ级时设防指标为：水平变形值ε≤1.5 mm/m，倾斜变形i≤2.5 mm/m。由预计结果可知，方案一的四种保护煤柱宽度下，地表变形均不满足设防指标要求；而方案二、方案三和方案四虽可满足地表建(构)筑物保护等级要求，但方案三和方案四充实率分别需要达到90%和95%，在提高充实率要求下要增加充填材料中的水泥等添加剂含量，在很大程度上提高了充填材料的成本投资，因此，在最大限度减少煤柱浪费的前提下，方案二充实率85%，煤柱宽度12 m为较优选择。

将煤柱宽度12 m，充实率85%作为矿井实际开采条件，充填开采后地表下沉400 mm，倾斜变形2.4 mm/m，水平变形1.4 mm/m，具体变形极值见表4，地表变形均在设防标准范围内，可达到安全生产的目的。

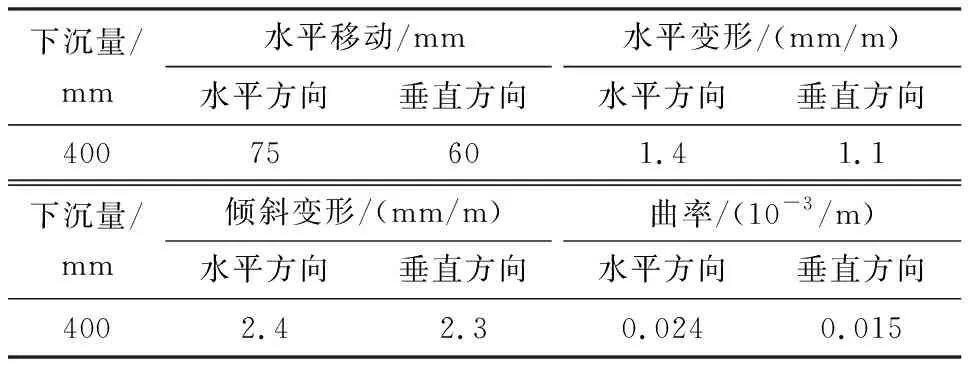
表4 充填开采后地表变形极值Table 4 Surface deformation extremum after filling mining

3.2 地表变形数值模拟结果及规律分析

最大下沉值、最大水平移动、下沉率和水平移动系数的数值模拟结果见表5。根据数值模拟结果分别对最大下沉值Wmax、最大水平移动Umax、下沉率q和水平移动系数r、煤柱留设宽度D和充实率η的关系进行拟合，具体如图3所示。

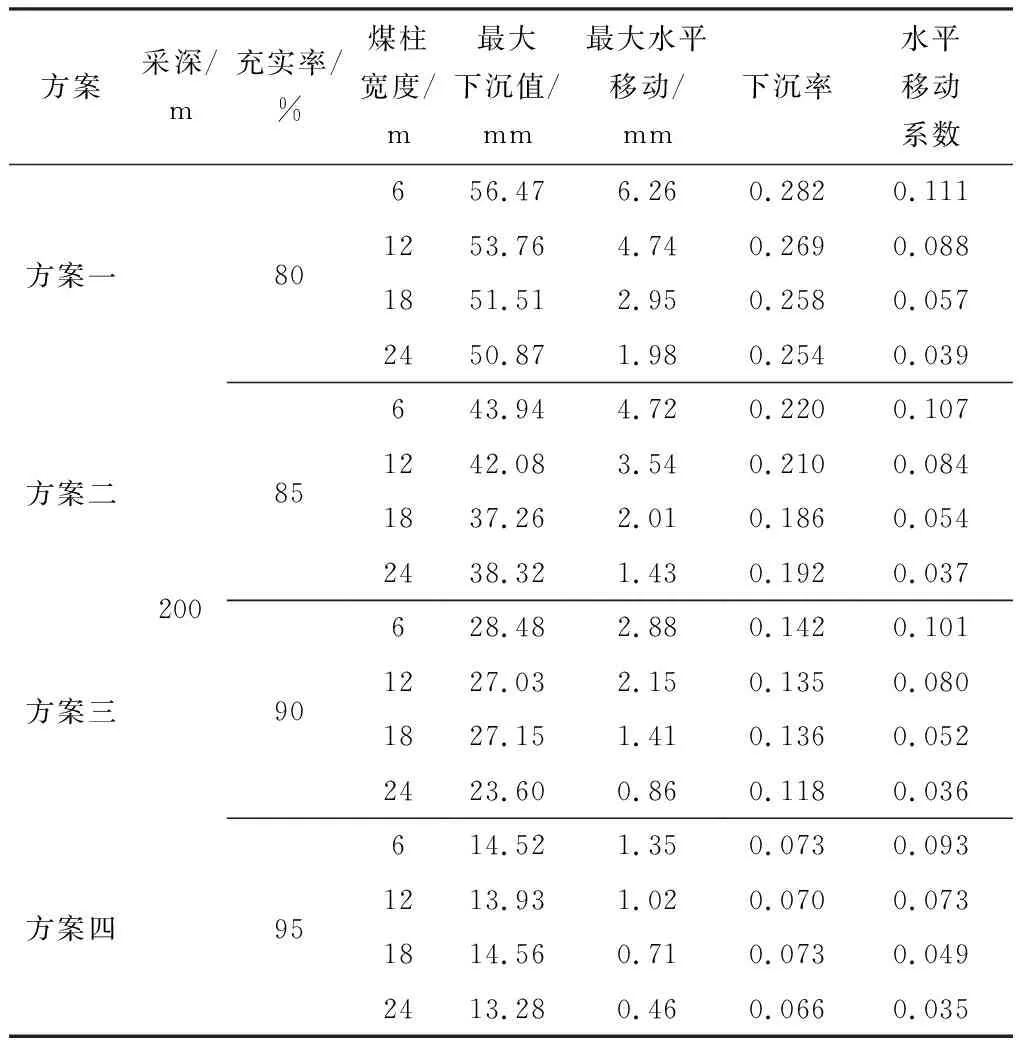
表5 不同开采条件下模拟开采地表变形结果Table 5 Simulation results of surface deformation under different mining conditions

图3 充实率、煤柱宽度拟合关系图Fig.3 Enrichment rate,coal pillar width fitting diagram

由图3可知，最大水平移动、最大下沉值、水平移动系数和下沉率均随煤柱宽度的增大呈降低趋势；最大水平移动、最大下沉值、水平移动系数和下沉率与煤柱宽度呈一次函数关系且斜率较小，这可能是采空区顶板受到超过其极限应力而发生破断弯曲，造成上覆岩层出现变形，上覆岩层变形传至地表，引发地表下沉现象，但因煤柱及充填体联合控制，地表下沉量较小。而由于上覆岩层自重，充填体在支承上覆岩层的同时，上覆岩层对充填体施加垂直向下的力，但采空区空间有限，且充填体具有一定的塑性特征，因此充填体在上覆岩层的压力下向两侧扩散变形，对两侧煤柱进行挤压，从而对两侧留设保护煤柱形成围压，在一定程度上加固保护煤柱。上覆岩层自重一定时，采空区充实率越高，充填体对两侧保护煤柱形成围压越大，随着充实率的提高，地表变形也随之减小。

根据充填开采数值模拟结果，绘制同一充实率时不同煤柱宽度地表下沉及地表水平移动曲线，如图4所示。由图4可知，保护煤柱宽度相同时，地表下沉值和水平移动值均随充实率的增大呈降低趋势；当充实率分别为80%、85%、90%、95%，保护煤柱为12 m时，地表最大下沉值分别达到53.76 mm、42.08 mm、27.03 mm、13.93 mm，地表最大水平移动分别达到4.74 mm、3.54 mm、2.15 mm、1.02 mm；与充实率80%相比，下沉幅度分别降低了21.73%、49.72%、74.09%，水平移动幅度分别降低了25.32%、54.64%、78.48%，说明充实率的提高可以有效抑制地表沉陷。充实率相同时，地表下沉值随着保护煤柱宽度的增大而逐渐减小，但以煤柱为中心的地表下沉并未呈现完全对称分布，这是由于两个充填工作面间保护煤柱宽度的影响；当保护煤柱为18 m和24 m时，地表下沉值曲线中部位置呈现盆地“平底”现象，说明地表达到充分采动，且地表沉陷曲线呈随煤柱宽度增大而出现盆地“平底”现象的趋势。虽然保护煤柱宽度增大，能够减小地表下沉，尽快达到地表充分采动，但是会浪费大量煤炭资源，也可能会影响工作面之间在煤柱位置呈现地面“凸起”的情况，对后期地表建(构)筑物可能产生影响。

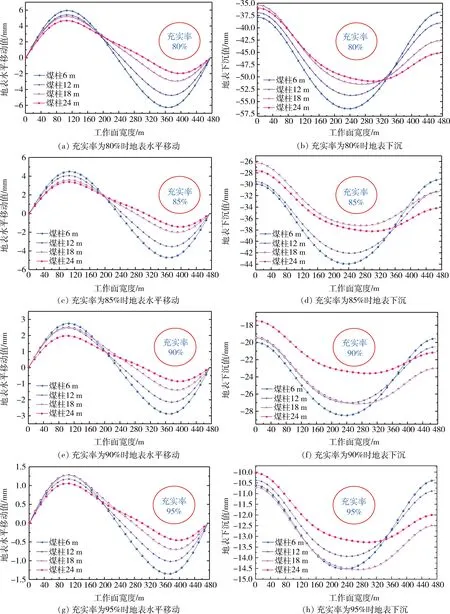
图4 不同充实率下地表变形规律Fig.4 Surface deformation law under different filling rate

保护煤柱内部应力随煤柱宽度增大逐渐降低，当充实率为85%时，不同宽度保护煤柱内部应力变化如图5所示。由图5可知，在充填开采过程中，采动破坏了原岩应力场的原始平衡状态，致使保护煤柱内部产生应力集中现象，应力以充填体为中心，呈对称变化，充填体内部应力最高，递减趋势向两侧扩展。 当煤柱由6 m增大到24 m，充实率为85%时，煤柱内部应力峰值分别达到27.48 MPa、21.85 MPa、19.79 MPa、17.94 MPa，煤柱内部应力峰值相比6 m宽度时，降幅达到20.48%，降低明显；当煤柱由6 m增大到24 m，充实率为95%时，保护煤柱内部应力峰值分别为17.04 MPa、12.77 MPa、10.32 MPa、9.82 MPa，应力峰值降低明显，在同一充实率下，随着煤柱宽度的增大，煤柱内部峰值应力逐渐降低。

当保护煤柱宽度固定时，随着充实率的增大地表下沉值以及水平移动值逐渐减少，在充实率为85%，保护煤柱12 m时，相较于6 m，煤柱内部峰值应力降幅达到20.48%，地表水平移动值由4.72 mm降低到2.78 mm，降幅达到41.10%，由此可见，煤柱宽度为12 m时，能够较6 m情况下很好地保护地表建(构)筑物；随着保护煤柱增至18 m和24 m，地表下沉值与水平移动值均有降低，煤柱内部应力峰值同时大大减小，更有利于保护地表建(构)筑物，但是从资源回采方面考虑，增大保护煤柱宽度，极大降低了井下煤炭资源回采效率。

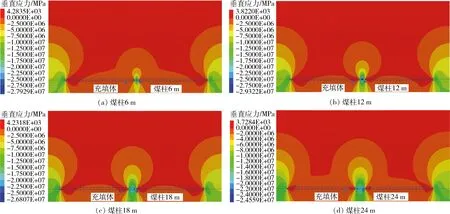
图5 充实率为85%时保护煤柱垂直应力变化Fig.5 Stress change inside protective coal pillar under filling rate of 85%

对比概率积分法预计结果和数值模拟结果发现，沉陷预计结果均大于数值模拟结果，是因为数值模拟研究将赋存条件进行简化，模型参数选取偏理想化，而实际赋存条件非常复杂，所以概率积分法与数值模拟结果有偏差，但采用概率积分法与数值模拟对地表变形规律是一致的，充填工作面地表建(构)筑物变形均控制在地表建(构)筑物保护等级Ⅰ级变形范围之内，未超出设防标准。

4 结 论

针对建筑物下压覆资源开采过程中，地表变形控制要求高的问题，采用等价采高概率积分法和数值模拟的方法研究了保护煤柱宽度6 m、12 m、18 m、24 m时的不同充实率下地表沉陷规律，具体结论如下所述。

1) 基于等价采高的概率积分法模型，对西金石料厂、牧民房屋、110 kV变电站等地表建(构)筑物进行地表沉陷预计，结果表明：充填开采参数选取充实率85%，煤柱宽度12 m(ε≤1.4 mm/m，i≤2.4 mm/m)较为合理且满足设防指标要求。

2) 当煤柱宽度相同时，随着充实率的提高，地表最大水平移动、最大下沉值、水平移动系数和下沉率均呈降低趋势；当充实率相同时，随着保护煤柱宽度的增大，地表下沉值逐渐减小，但以煤柱为中心的地表下沉并未呈现完全“非对称”分布，且呈随煤柱宽度增大而逐渐显现盆地“平底”现象的趋势。

3) 留设保护煤柱6 m、12 m、18 m、24 m时充实率达到80%、85%、90%、95%的应力变化规律：以充填体为中心的应力变化呈对称分布，其中，充填体内部应力最大，递减趋势向两侧扩展；当充实率为85%，保护煤柱12 m时，充填体内部最高应力为21.85 MPa。