利用待定系数法巧求数列的通项公式
朱 磊
(江苏省新海高级中学 222006)
处理某些特殊类型的数列问题时,可灵活运用“待定系数法”,需要先构造等比数列,再利用等比数列的通项公式即可顺利获解.请结合以下归类解析,认真领会构造等比数列的关键点以及易错点,以便逐步提高运用能力,进一步提升数学抽象方面的核心素养.
1递推式中含有关于n的代数式,巧求通项公式
如果数列an的递推式为an+1=kan+f(n)(其中k为非零常数,f(n)是关于n的代数式),那么可灵活运用“待定系数法”构造等比数列,巧求数列an的通项公式.
说明当k=1时,可灵活运用“累加法”迅速获解,没有必要利用“待定系数法”.
1.1若f(n)是关于n的幂式,可巧求通项
例1已知数列an的首项a1=1,且满足an+1+an=3·2n,求数列an的通项公式.
解析因为数列{an}中,an+1+an=3·2n,
所以移项得
an+1=-an+3·2n.
①
于是,可设存在实数x使得
an+1+x·2n+1=-(an+x·2n),
则an+1=-an-3x·2n.
②
从而,对比①②两式可得
-3x=3,
即x=-1.
因此,可得an+1-2n+1=-(an-2n).
故可知数列an-2n是以a1-2=-1为首项,以-1为公比的等比数列.
从而,根据等比数列的通项公式得
an-2n=-1×(-1)n-1.
化简,得an=2n+(-1)n.
评注本题利用“待定系数法”构造等式时,必须满足an+x·2n和an+1+x·2n+1是一个数列的相邻两项;其次,必须准确运用等比数列an-2n的通项公式解题.
1.2若f(n)是关于n的一次式,可巧求通项
例2 已知数列an中,a1=2,an+1=-2an+3n+3,求数列an的通项公式.
解析因为数列{an}中,
an+1=-2an+3n+3,
③
所以可设存在常数a,b使得
an+1+a(n+1)b=-2(an+an+b).
整理,得an+1=-2an-3an-a-3b.
④
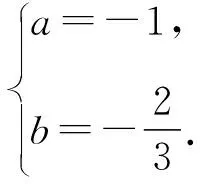

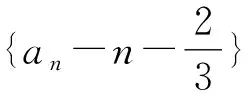
从而,由等比数列的通项公式可得
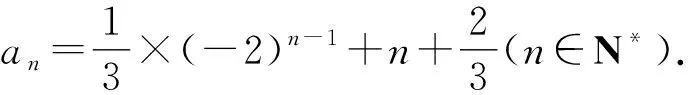
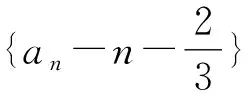
1.3 若f(n)是关于n的二次式,可巧求通项
例3 已知数列an中,a1=1,an+1+2an=n2+3n+3,求数列an的通项公式.
解析在数列{an}中,由题设可得
an+1=-2an+n2+3n+3.
⑤
所以可设存在常数a,b,c使得
an+1+a(n+1)2+b(n+1)+c=-2(an+an2+bn+c).
整理,得
an+1=-2an-3an2-(2a+3b)n-a-b-3c.
⑥
于是,由⑤⑥两式可得
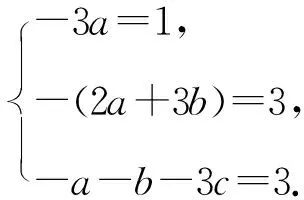
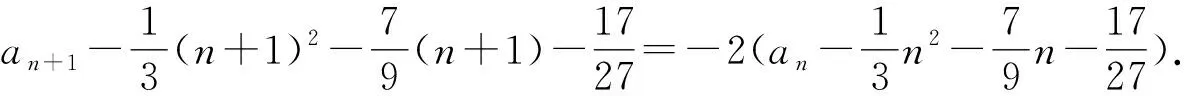

从而,由等比数列的通项公式可得
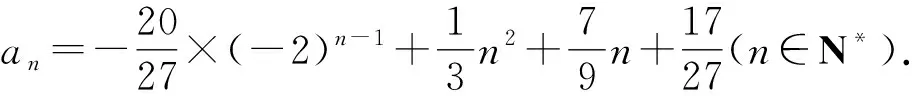
评注本题利用“待定系数法”构造等式时,必须满足an+an2+bn+c和an+1+a(n+1)2+b(n+1)+c是一个数列的相邻两项;其次,要注意在新情景下,准确运用等比数列k的通项公式解题.
2 斐波那契数列及其通项公式的求解
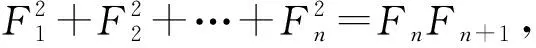
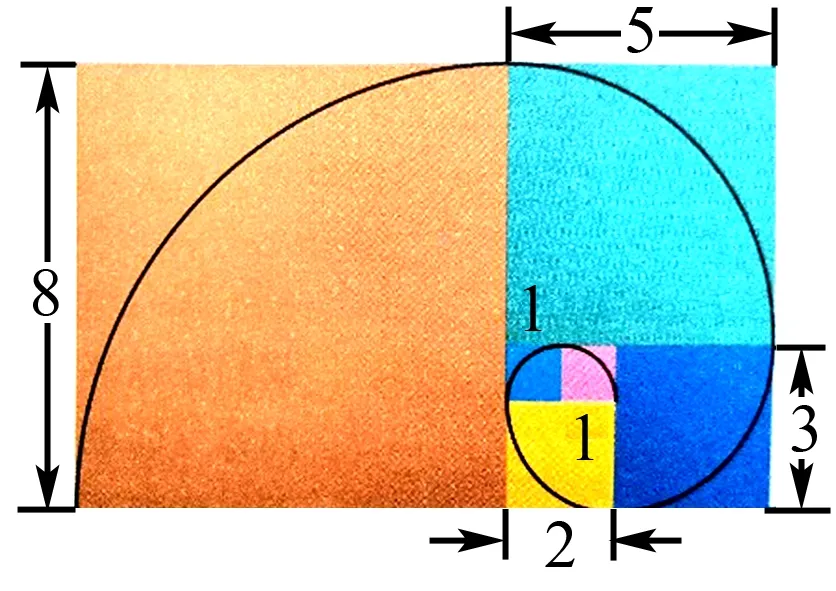
图1
例4已知数列Fn是斐波那契数列,即满足F1=F2=1,且Fn=Fn-1+Fn-2(n≥3),求数列Fn的通项公式.
解析由于数列Fn的递推式为
Fn=Fn-1+Fn-2(n≥3),
⑦
从而可设存在常数r,s使得
Fn-rFn-1=s(Fn-1-rFn-2)(n≥3),
整理,得
Fn=(r+s)Fn-1-rsFn-2.
⑧
于是,对比⑦⑧两式可得r+s=1,-rs=1.
因此,根据韦达定理可知r,s为一元二次方程x2-x-1=0的实数根.
⑨
⑩
从而,由⑨⑩可得

故所求数列Fn的通项公式为
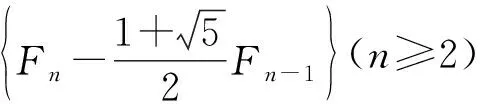
综上,分析、解决某些特殊类型的数列问题时,学会灵活运用“待定系数法”,往往可获得“事半功倍”之效.同时,有利于较好地培养数学抽象思维能力、推理论证能力以及运算求解能力.故创新思维能够强化学生的探究精神,提高对所学知识、方法的运用能力.

