基于数字体图像相关法的TATB 基PBX 材料内部变形测量

王延珺，邹 翔，潘 兵，郭昱辰，刘 晨，韩 超，吕珂臻

（1. 中国工程物理研究院化工材料研究所，四川 绵阳 621999；2. 北京航空航天大学固体力学所，北京 100191）

0 引言

高聚物黏结炸药（Polymer Bonded Explosives，PBX）作为一种高能炸药晶体和高聚物黏结剂组成的复合材料，因其具有能量高、钝感、耐热的优点，在国防工业中得到了广泛应用。PBX 材料中的炸药晶体和黏结剂在含量、热物理性能方面均存在较大差异，因此组分之间存在性质各异的界面。同时，PBX 材料是一种典型的脆性材料，其抗拉强度较低，力学性能极易受振动、冲击、热加载等环境因素影响［1-3］。将PBX 材料压制成型为部件时，内应力释放机制会使成型部件发生弹性回弹，影响其稳定性。此外，PBX 材料在热处理、机械加工、运输及存储过程中产生的内应力会使晶体断裂、界面脱粘、黏结剂基体开裂，造成PBX 材料力学性能的下降［4-5］，因此极需了解PBX 内应力演化规律及微细观结构演化机理的识别方法。

现有PBX 的原位力学性能测试方法主要有接触式与非接触式，然而都存在一定局限性。如采用表面贴片应变计测量炸药部件的力学响应时，由于PBX 材料属于非均匀材料，所获得的测量值仅能反映小范围被测表面的平均效应；若采用预埋传感器测量，介入式传感器会改变材料内部结构，引入较大的测量误差。非接触方法相比于以上接触式方法，能够极大地减小测量误差，主要有射线法、光测力学法。基于布拉格晶格衍射原理的射线法（X/中子衍射）仅能获得浅表层小体积内的晶格畸变，从而可以反映出束斑区域的晶体变形信息［6］。然而，对PBX 材料的裂纹检测多见于晶体与高分子黏结剂的界面失效［2］。因此，射线法无法反映高分子粘结剂对PBX 复合材料的三维应变应力响应的影响。近10 余年来，利用光测力学手段，如数字图像相关方法（Digital Image Correlation，DIC）测量PBX 材料在热力作用下的表面位移场及应变场开始兴起［7］。然而2D-DIC，3D-DIC 仅可用于表面变形测量［8］，获取的是材料表面位移的2 个或3 个自由度分量。非均匀材料的表面变形场分布与内部变形场分布往往有显著的差异，仅依赖表面的位移分析并不能得到非均匀材料体系内部变形的准确信息。故而，常规测试手段无法实现PBX 这种多晶、多界面、非均质的复杂材料体系在外载荷作用下的的三维力学响应表征。

基于X 射线微焦点计算机断层扫描（μ-CT）技术和数字体图像相关（Digital Volume Correlation，DVC）算法的物体内部变形测量技术是实验固体力学的前沿研究方法。作为可用于不透明固体材料内部变形场测量的实验力学技术，DVC 方法在实验力学、岩土力学、材料科学、生物医学等领域受到关注［9］，在含能材料领域内研究刚刚起步。美国Los Alamos 国家实验室的研究团队利用IMPULSE 同步辐射先进光源APS，对奥克托今（HMX）基PBX 炸药在动态压缩实验进行了表征和追踪，测量了冲击过程的晶体破碎形貌，但未能对应力应变演化进行深入分析［10］。法国巴黎萨克雷大学的Hild［11］与法国军用核能中心CEA-Gramat 研究团队将DVC 方法应用于ESRF 加速器CT 原位观测下的HTPB 推进剂材料单轴拉伸实验，通过计算全局体积应变获得材料在不同载荷状态下的泊松比，通过局部分析各计算单元内的平均应变获得模拟材料晶体与黏结剂2 种主要组分的非均匀变形状态，并且DVC 法的灰度残余分布图能够精确地表明材料的损伤程度与开裂机理，该方法对于揭示含能材料内部变形机制具有重要意义［11］。英国牛津大学的Siviour 等［12］借助原位CT 实验，利用DVC 法获得了含能材料造型粉颗粒在压制过程中的三维位移场、应变场等高精度信息，DVC 方法获得的材料单轴压缩力学响应与有限元仿真模型数值预测结果符合度良好，为进一步推导应力场分布提供了必要条件。该团队与Los Alamos 国家验室将DVC 方法应用于PBX 试样在单轴压缩过程中的变形测量，揭示了内部不均匀应变场分布与细观结构演变的关联关系，挖掘出丰富的力学信息：内部单个造型粉颗粒的运动，内部裂纹的形成与拓展，黏结剂与晶体的脱粘以及试样的断裂机制。美国德州大学达拉斯分校的Hu 等［13］采用DVC 方法测量了曼森砂在围压实验中的内部应变场，并通过分析各个颗粒的最小本征应变值评估了压缩过程中的力链形成与演化过程［14］，对于揭示颗粒材料体系压制成型的机理机制具有重要意义。北京航空航天大学的潘兵等［15］利用自己开发的增量DVC 算法系统研究了推进剂代用材料在单轴压缩实验过程中压缩应变从10%增加到70%过程中其内部应变场变化情况。由此可见，该方法能够定性定量地分析含能材料在原位力学实验中的变形状态，对于开展相关研究具有一定的参考意义。当晶体颗粒填充比例较低时，所获得的数字图像灰度对比度大，对变形状态的测量相对容易实现。

为此，本研究将基于μ-CT 和DVC 结合的方法应用于TATB 基PBX 材料内部变形测量的探索。由于PBX 内部组分密度接近，数字图像灰度值对比度相对较低，在小变形状态下即会发生断裂，因而研究在采用μ-CT 对单轴压缩下的PBX 圆柱试件进行了体成像扫描后，为提高内部组分纹理对比度，将图像进行预处理，采用自编程的基于C++语言的局部DVC 算法，对所得PBX 的CT 成像的灰度图原始数据进行计算，揭示了TATB 基PBX 材料在单轴压缩实验中的三维内部变形状态，并提出了通过DVC 计算获得的零均值归一化互相关（zero-mean normalized cross-correlatio，ZNCC）系数分布图来判定亚体素裂纹的空间位置的方法。

1 原位实验与图像分析方法

1.1 TATB 基PBX 材料单轴压缩实验

样品试件：TATB 基PBX 试件为120 ℃、150 MPa压制的直径为10 mm、高度为10.2 mm 药柱（图1），药柱密度为1.876 g·cm-3。

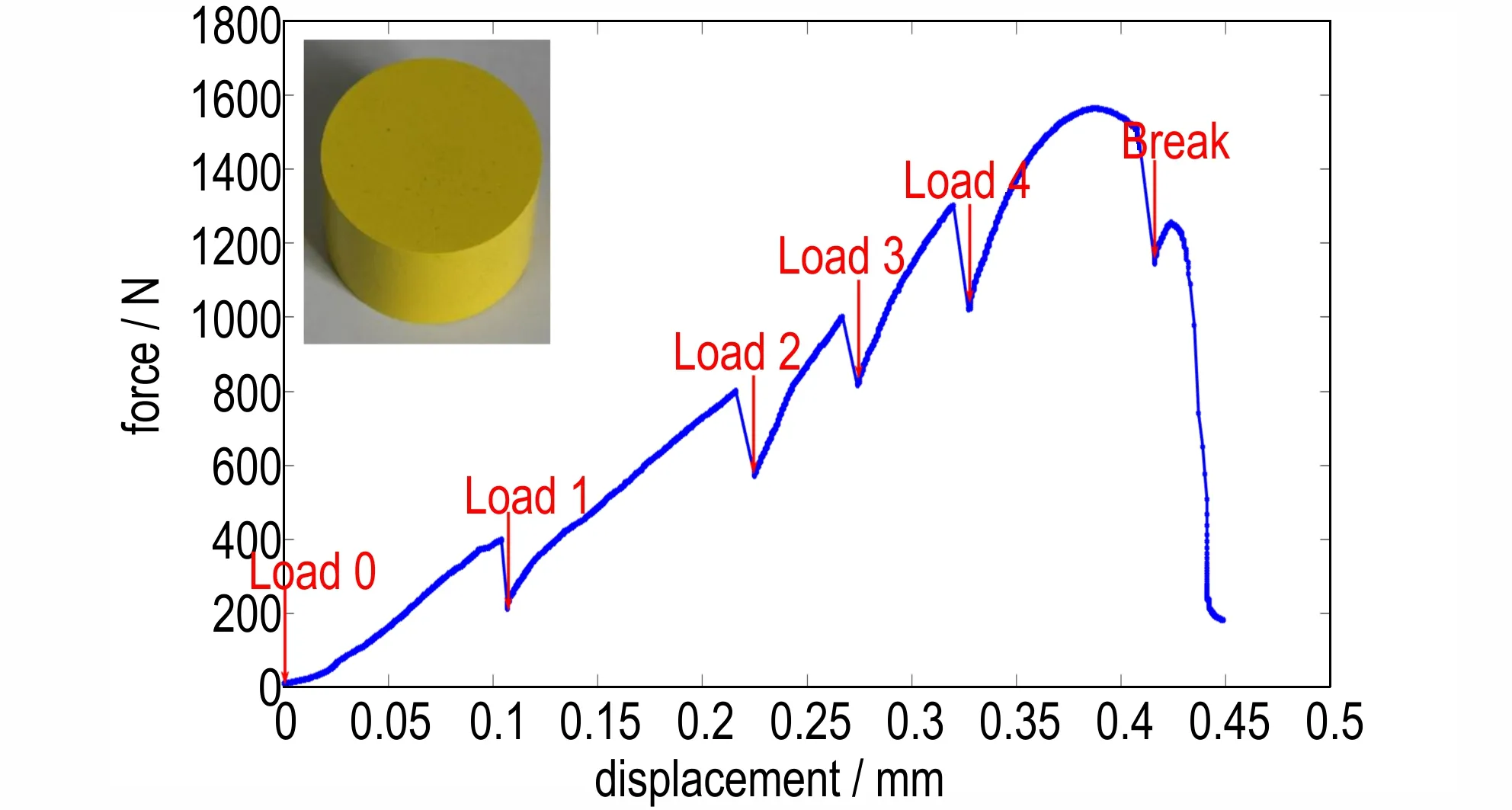
图1 TATB 基PBX 材料试件在单轴压缩下的力-位移曲线Fig.1 Loading curve of TATB-based PBX sample under uniaxial compression test

仪器：单轴压缩实验采用配置Deben Microtest CT5000-TEC 原位加载装置的原位μ-CT 进行。

实验方法：室温下对TATB 基PBX 试件进行同步的单轴压缩实验和CT 观测。为采集压缩过程中的变化图像，实验对样件加载后，再进行CT 扫描。由于应力松弛，载荷均会出现下降，因此不同的时刻进行CT 扫描后继续进行加载，如此循环加载扫描步骤，直至试件发生破坏后停止实验，本研究为此连续进行5 次加载。加载模式为位移加载模式，加载速率为0.1 mm·min-1，实验力-位移载荷如图1 所示。CT 扫描电压为100 kV，电流为100 μA，曝光时间为0.6 ms，试件旋转过程中每隔0.33°采集1 张图像，共采集1080 张图像，获取的体 图 像 尺 寸 为550 voxel×550 voxel×500 voxel。实验过程中保持CT 扫描参数相同，以减小测量参数对结果的影响，保证在相同条件下对试件内部形变带来的灰度变化进行追踪，进而实现对内部变形及损伤演化的定量分析。实验中调节样品与探测器之间的距离，使TATB 基PBX 材料的CT 体图像分辨率为19.8 μm。

1.2 数字体图像相关法(DVC)

数字体图像相关法（DVC）可通过对比分析数字体成像设备得到的试件变形前后的2 组数字体图像，经由计算感兴趣区域内的灰度变化获得物体内部亚体素精度的三维位移场和全场应变［9］。DVC 法分析主要包括以下3 个步骤：

（1）数字体图像的采集：采用体成像设备对不同加载状态下的试件进行扫描，得到试件的数字体图像；（2）三维位移场的测量：通过体图像配准算法［9］确定参考体图像中各离散计算点在目标体图像中的位置，获得全场三维位移；（3）三维应变场计算：利用数值微分方法处理得到三维位移场，获得三维应变场。

为此，本研究通过单轴压缩实验获取了4 种载荷状态下的试件体图像。为准确研究试件变形引起的部分计算点灰度变化，同时对图像进行了预处理，以提升体图像纹理对比度，进而保证DVC 计算精度。用DVC 对原始图片直接进行处理，在4 种载荷下，基于C++编程的DVC 算法对原始图片的计算速度分别为8.26 点/秒，7.53 点/秒，6.22 点/秒 和5.11 点/秒，从 计算时间看，随着载荷的加大，试样变形越大，故而所需计算时间越长。

三维应变场获取的关键是三维位移场的测量精准度。为确定某计算点的三维位移矢量，需要围绕该点选择包含足够灰度对比度的立方体参考图像子体块，并建立一个可定量评价参考图像子体块和待寻找的目标图像子体块相似程度的目标函数。本研究采用零均值归一化互相关（zero-mean normalized sum-of-square difference，ZNSSD）函数来评价2 子体块的相似程度［18］。由于目标图像子体块可能出现包括平移、转动、均匀应变甚至更为复杂的非均匀变形，因而需要采用包括12 个变量的一阶形函数［16］来近似其内部变形，再通过数值优化算法和灰度插值算法相结合来优化目标函数，以在变形后的体图像中寻找与图像子体块最为相似的目标图像子体块，从而确定其当前体素点（参考图像子体块中心点）的位移矢量。通过简单的整体素搜索，DVC 能快速确定各计算点的整体素位移。随后，为了提高测量精度，需要采用亚体素配准算法对整像素结果进行优化以获得具有亚体素精度的位移结果，这一过程通常被认为是提高DVC 测量精准度的关键［9］。在众多亚体素位移算法中，反向组合高斯-牛顿算法（Inverse Compositional Gauss-Newton，IC-GN）因为具有计算精度和计算效率高等优点被广泛应用。本研究采用最新的三维IC-GN 配准算法，插值方法采用3 次B 样条插值方法，形函数采用一阶形函数，应变计算采用逐点最小二乘（pointwise least-square，PLS）算法进行运算。

为了保证计算效率和精度，使计算能够在普通计算机中使用DVC 方法对高分辨率体图像进行分析，本次分析采用逐层可靠性导向的初值估计策略为计算点提供位移初值［17］，由于在加载过程中，试样没有发生较大的旋转运动，因此可靠性导向种子点的位移初值采用简单的整体素搜索方法。与现有文献中提出的常规三维可靠性导向位移跟踪方法不同，逐层可靠性导向方法仅仅引导每个计算层内的计算路径并传递相邻计算层之间的变形矢量以保证初值精度。

2 结果与讨论

2.1 体图像预处理对DVC 结果的影响

在DVC 计算中，ZNCC 系数（变化范围为［-1，1］）被广泛应用于判断DVC 计算点的匹配程度，ZNCC 系数越高，说明计算点的参考子体块和变形子体块匹配越好，此时获得的位移场精度越高，相反地，当一计算点的ZNCC 系数低于某一设定值时就认为该点匹配失败，位移场误差较大［9］。为了获取较高的ZNCC 系数，研究采用降噪方法对试件的体图像图像进行了预处理，并对比分析了预处理前后的DVC 计算结果。

图2 为原始CT 体图像预处理前，DVC 计算得到的各计算点处的ZNCC 系数分布图。由图2 可以看出，在4 种载荷下，各计算点ZNCC 系数均较低，均值仅分别为0.696、0.672、0.670 和0.668，这主要是由于试件体图像内部体图像特征不明显，抗噪声能力较弱；此外，随着载荷的增加，计算点ZNCC 系数均值呈现小幅度下降趋势，分析认为这主要是因为试件变形造成了部分计算点的灰度变化。可见，直接对试件CT 的原始图片进行DVC 计算，所得的结果较差。因此接下来将会对原始图像进行预处理以提高DVC 结果的准确性。

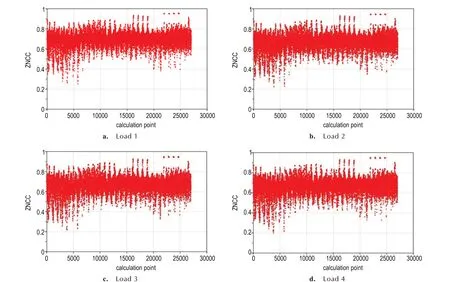
图2 采用原始CT 体图像不同载荷下各计算点ZNCC 系数分布情况Fig.2 Distribution of ZNCC coefficient using original CT volume images under different loading states

在DIC 测量中，操作者可在被测试样表面制作人工散斑图案以提供高对比度的变形信息载体。在绝大多数情况下，DVC 方法只能依赖被测物体内部的复杂成分或微结构体系在体图像中形成的灰度差异作为变形信息载体，因此体图像的质量对DVC 的计算精度影响较大。相比于具有良好对比度的材料（如岩石、泡沫等）以及具有大量内含物的材料（如球墨铸铁、铝铜合金等），PBX 材料组分密度接近，内部纹理天然较弱。为了提高DVC 的测量精准度对图像进行处理，图3 为预处理前后灰度分布直方图，图4 为预处理前后试件体图像和切片图。由图3a 可以看出，原始图像中大量体素点灰度值集中在0～150，导致图像整体偏暗，难以辨别（图4a）。为了解决这个问题，将灰度值大于130的体素点直接设为0（这些点属于噪声点），然后将剩余体素点灰度值拉伸到0～255，拉伸公式见式（1）。由图4b 可知，实验试件内的灰度进行优化处理后，对比度有所提升，可以辨别试件内的颗粒边界。剩下4组变形体图像均进行类似操作。

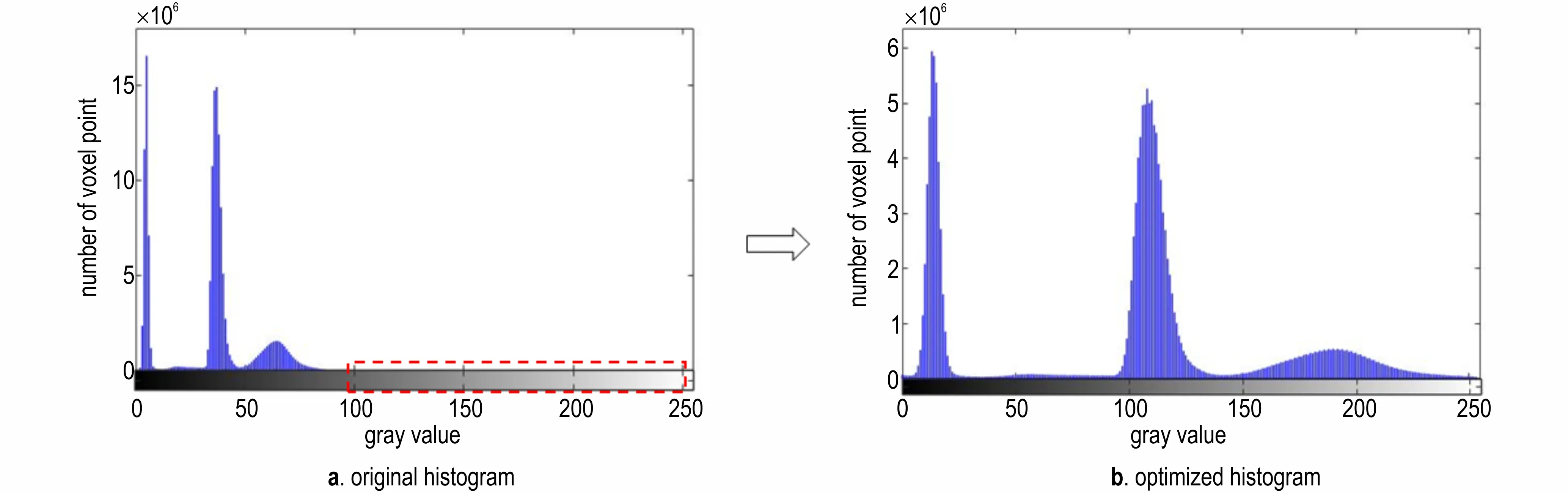
图3 实验试件体图像优化前后灰度分布直方图Fig.3 Histograms of original CT image and optimized CT image

图4 优化前后的试件体图像和切片图Fig.4 Comparison between original CT image and optimized CT image

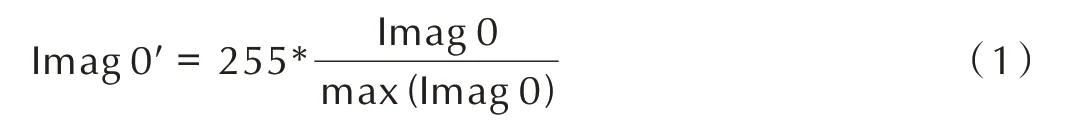
图5 为实验试件内的灰度进行优化处理后，4 种不同载荷下各计算点ZNCC 系数分布情况。由于PBX 材料是脆性材料，在外载荷作用下，发生较小的变形即会断裂，故而图5 中ZNCC 系数分布大体一致。由图5可以看出各计算点ZNCC 系数均得到提升，均值高于0.75。这是因为作为变形信息载体的内部纹理的对比度提高，体图像的噪音大大降低，可见，预处理对于提升DVC 计算精度具有较大的影响。

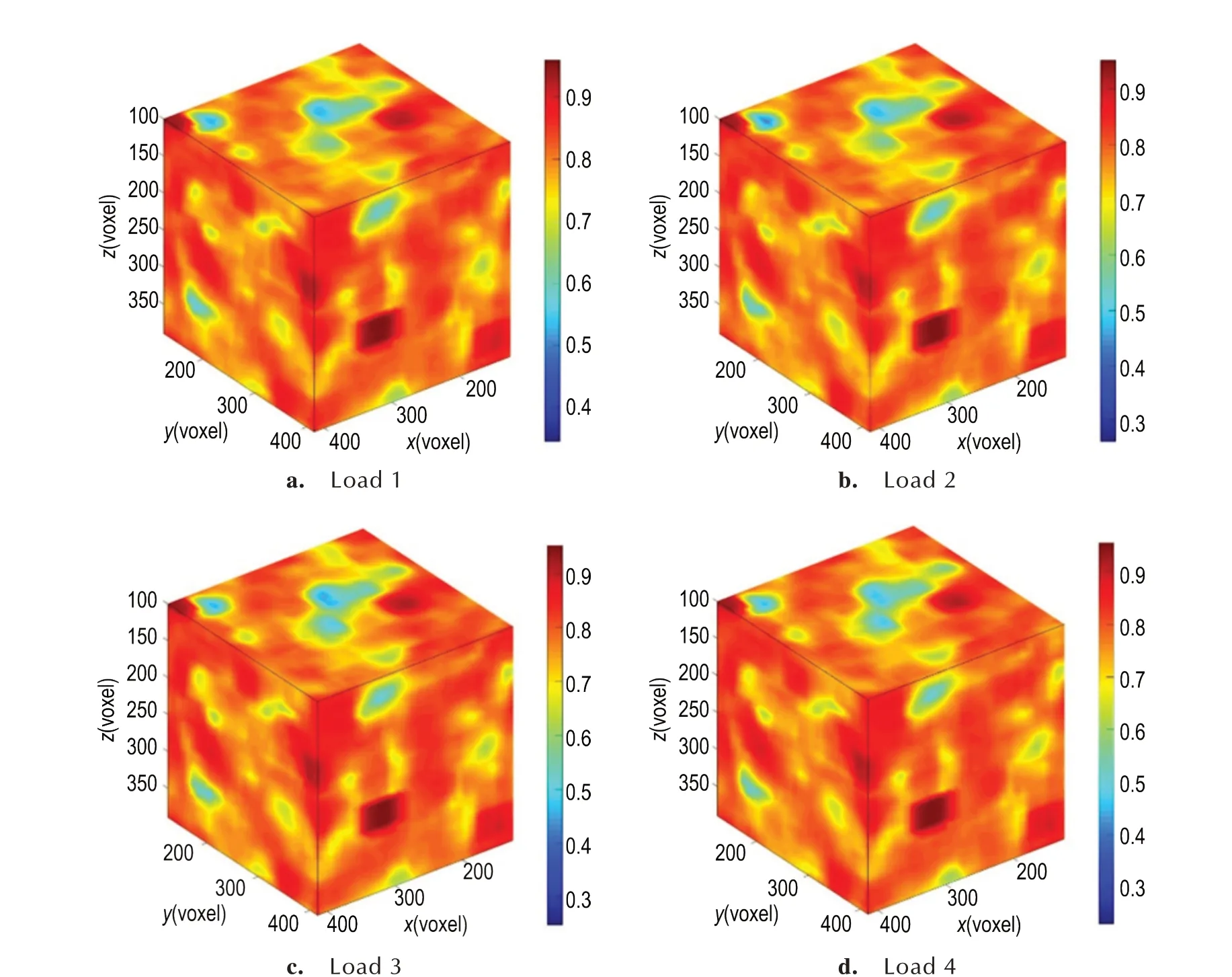
图5 不同载荷下各计算点ZNCC 系数分布情况Fig.5 Distribution of ZNCC coefficient of optimized CT images under different loading states

2.2 单轴压缩实验过程中的位移场

在进行DVC 分析前，为了降低图像噪声对测量精度的影响，利用高斯滤波器（尺寸为5×5×5，标准差为1）对4 组体图像进行高斯滤波［18］。然后，在滤波后的参考体图像中心选取尺寸为300 voxel×300 voxel×300 voxel 的感兴趣区域（Volume of Interest，VOI）。在DVC 计算时，将每次加载获得的体图像（变形体图像）分别与加载前采集的体图像（参考体图像）进行匹配，采用3D IC-GN 亚体素配准算法，最优收敛条件为：位移矢量增量的模小于0.001 voxel 或迭代次数不超过20 次，子体块尺寸为41 voxel×41 voxel×41 voxel，计算步长为10 voxel，共有30×30×30=27000 个均匀分布的计算点。在4 种载荷下，DVC 计算速度分别为8.31，8.02，7.31 点/秒和6.45 点/秒，可以看出试样变形越大，所需计算时间越长。

在4 种载荷下，大部分计算点ZNCC 系数较高，4种载荷下ZNCC 系数均值分别为0.798，0.772，0.770和0.768，均在0.75 以上，因此结果具有较高的可靠性；与此同时，随着载荷的增加，计算点ZNCC 系数均值呈小幅度下降趋势，这主要是由于试件变形引起部分计算点灰度变化而引起的。为了保证计算结果的可靠性，需要将ZNCC 系数较低的计算点剔除。根据计算 结 果，将0.75 设 为ZNCC 阈 值，ZNCC 低 于 该 阈 值的计算点将被剔除，这些点的位移结果（包括位移u，v，w）将通过周围ZNCC 系数高于0.75 的计算点插值得到。在4 种载荷下，ZNCC 系数高于所设阈值的点分别为23325、19356、19356 个和18497 个，占总共27000 个点的比例分别为86.3889%、71.6889%、70.0185 %和68.5074 %，均大于65%，因此计算结果具有较高的可靠性。

图6 给出了在不同载荷下各计算点的u、v、w位移场。由图6 可知，获得的位移场表现出极大的非均匀性，主要原因为试件内部结构各向异性；造型粉颗粒的尺寸及大小呈现非均匀分布，因此在加载过程中各点位移差别较大。与此同时，由图6 可知，在载荷1 下位移u的最大值和最小值分别为10.9906 voxel 和9.0158 voxel，在载荷2 下位移u的最大值和最小值为11.2879 voxel 和7.8982 voxel，在 载 荷3 下 位 移u的最大值和最小值为12.4122 voxel 和7.8921 voxel，在载荷4 下位移u的最大值和最小值为11.9612 voxel和8.0347 voxel。在4 种载荷下，相对位移u而言，位移v值较小，其变化范围依次为［-2.6380 voxel，0.1821 voxel］、［3.0077 voxel，9.4698 voxel］ 、［3.2914 voxel，9.3240 voxel］和［2.4368 voxel，8.9796 voxel］，这说明在加载过程中试件在x方向还存在滑移。相对于位移u、v，位移w的变化更加均匀，这主要是由于z方向是加载方向，各点变形比较大，结果信噪比较高。

2.3 应变应力结果的分析

研究通过对每次加载获得的变形体图像与参考体图像的灰度进行亚体素配准计算分析，获得了不同载荷下各计算点的u、v、w位移场，结果如图6 所示。由图6 可以看出随着单轴压缩载荷的增加，感兴趣区域内的位移逐步增大，且由于非均匀材料体系特征，位移分布也体现出不均匀性。然而材料的力学性能由其受外载荷下的应力应变响应所反映，基于获得的三维位移场采用合适的差分算法即可获得应变场。

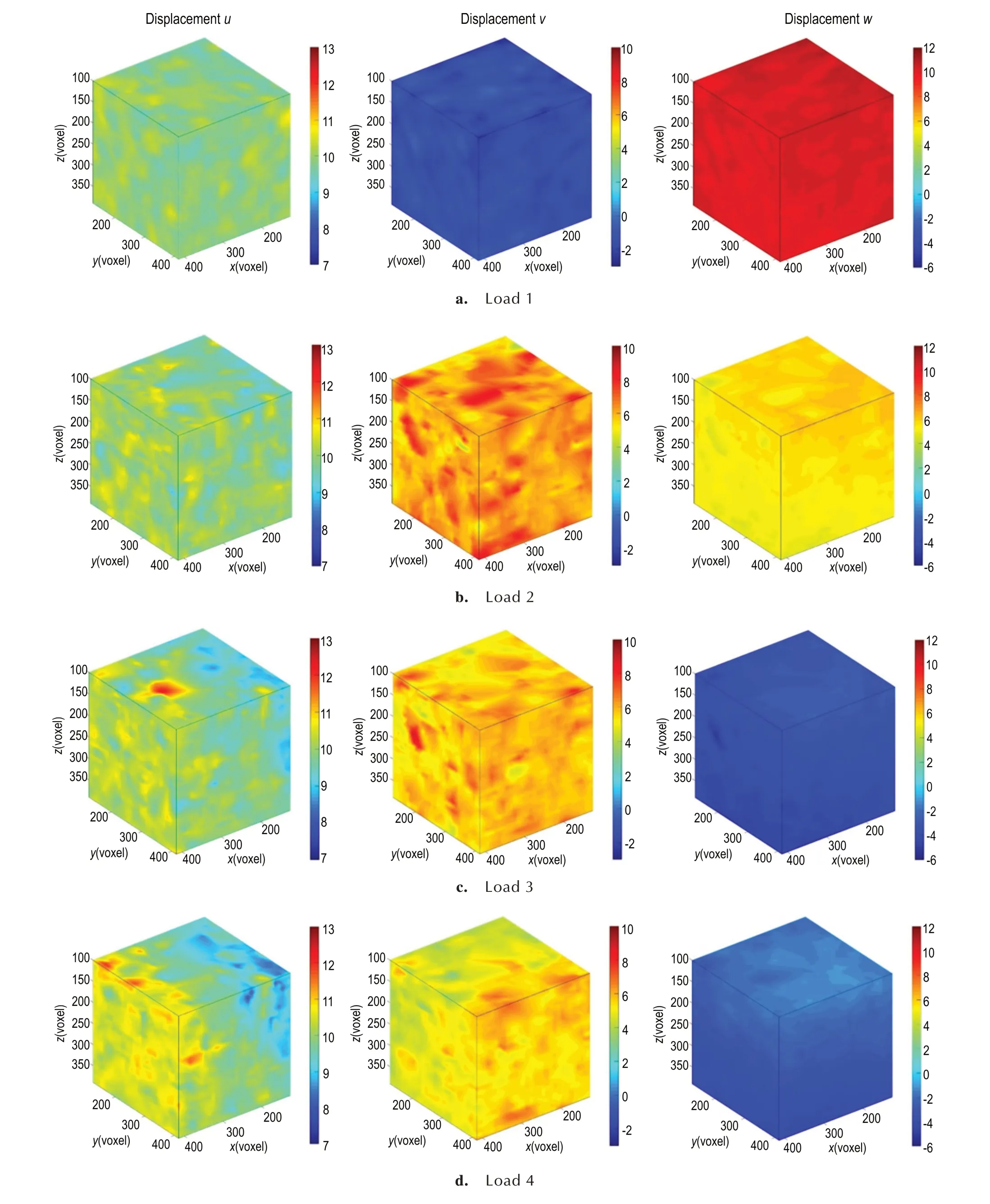
图6 不同载荷下位移场Fig. 6 Displacement fields under different loading states

由于各种因素的影响，该三维位移场不可避免地包含噪声，因此本研究采用逐点局部最小二乘拟合法计算各计算点的位移场，应变窗口大小为11×11×11。由于应变计算时间较短，约为5 s，因此不再给出具体的应变计算时间。为了更加直观地展示应变结果，结果如表1 所示，试件内部6 个应变分量（εxx，εyy，εzz，γxy，γxz，γyz）在不同载荷下的平均值。

由表1 可知，最大应变为单轴载荷方向εzz，当载荷稳定以后，从载荷2 开始，平面内应变εxx≅εyy，3 个切应变分量的变化较小，且均维持在较低水平。试件沿x、y方向的主应变相差不大，这说明试件沿压制面内的2个方向的力学性能差别较小，应变测量结果符合模压单向压缩成型的PBX 材料的力学特征。

表1 不同载荷下试件内部各应变分量平均值Table 1 Mean value of strain component under different loading states

根据加载过程中的载荷力-位移关系，表2 给出了每个加载步中应力-应变曲线的拟合直线，由表2 可知，由载荷0 状态到载荷1 过程中，拟合直线的斜率为532.25 MPa；从载荷1 到载荷2，拟合直线的斜率为649.13 MPa；从载荷2 到载荷3，拟合直线的斜率为1317.00 MPa；从载荷3 到载荷4，拟合直线的斜率为1372.30 MPa。

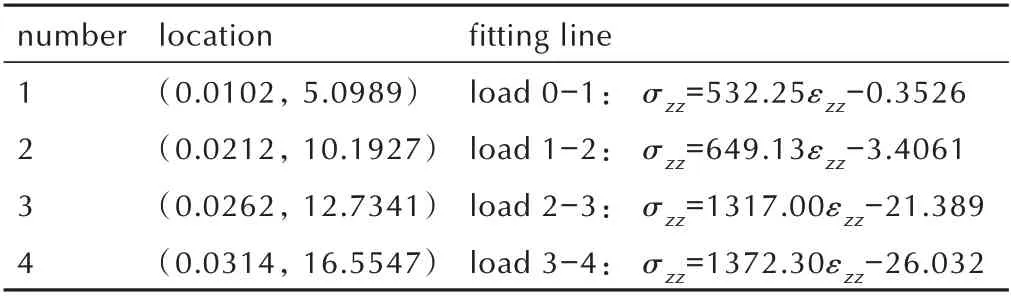
表2 不同载荷阶段应力应变线性拟合曲线Table 2 Linear fitting curve of stress-strain relationship under different loading states

通过前期材料力学实验测得该种材料的弹性模量E为729.60 MPa，泊松比ν为0.368，通过对比本次原位压缩实验结果，可近似认为在载荷2 之前材料均处于弹性阶段。为了更加直观地展示试件在压缩载荷下的变形情况，在载荷1 和2 下，通过胡克定律弹性本构关系，即可求得沿加载方向的弹性应力场σzz在试件内的分布［1］，见公式（2）。由于TATB 基PBX 材料本身是由尺寸、形状各异的造型粉颗粒压制而成，其结构的高度非均匀性导致试件在单轴压缩作用下的变形也是不均匀的。由于TATB 基PBX 材料含有随机分布的张开或闭合的初始损伤微裂纹，在材料只承受单向压缩载荷时，由于其微结构的局部非均匀性，试件中存在局部的拉伸应力集中［1］。而TATB 基PBX 材料的力学性能对拉伸载荷更为敏感，拉伸开裂是微裂纹激活和扩展的主要形式［2］。为了揭示TATB 基PBX 材料的断裂机制，根据DVC 算法获得的应变张量的6 个分量，即可采用胡克定律对试件的应力分布进行分析。如图7 所示，沿载荷方向的应力场（σzz）分布中有局部拉应力集中现象，材料的损伤和破坏往往是由这些集中区域开始。值得注意的是，对TATB 基PBX 材料内部应力场的分析，还需要考虑材料物理性能的各向异性，借助于多轴非线性本构关系的发展，以更精确地揭示外载荷下TATB 基PBX 材料的变形非均匀性和破坏机理。

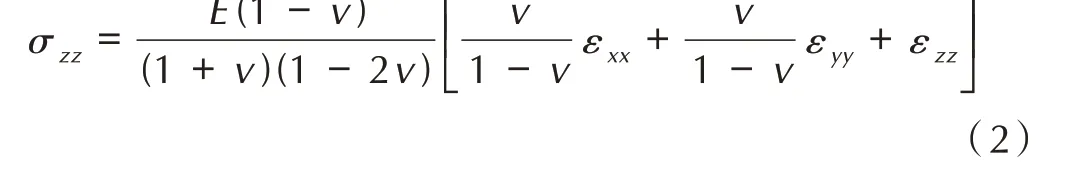
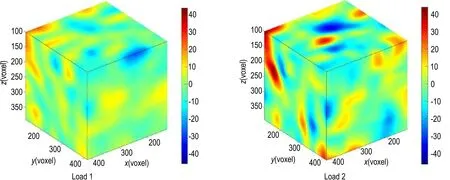
图7 三维应力场σzz（MPa）弹性阶段Fig.7 Stress distribution of σzz（MPa）during elastic state

2.4 基于ZNCC 系数局部化的裂纹分析

受μ-CT 设备分辨率的限制，在对内部裂纹的研究中，主要是观测大于μ-CT 空间分辨率的裂隙。在裂纹萌生阶段，由于宽度较小，往往肉眼不可见，容易被忽略。小于μ-CT 尺度的微裂纹难以从图像中直接观测，从而影响了对裂纹孕育发展全过程的揭示。微裂纹的存在会使得采集到的参考体图像与变形体图像中的灰度局部不守恒，通过DVC 方法分析获得的全局应变场分布中能够测得变形局部化区域，进而对低于μ-CT 分辨率的微裂纹进行探测。通过应用数字图像相关方法的计算参数，如利用灰度残余分布、相关性系数、局部应变集中等参量，能够很好地对材料内部的损伤进行量化表征，如已有研究中对颗粒材料的应变场局部集中分布［19］，对奥氏体不锈钢材料的灰度残余局部集中分布的量化分析［20］，均观测到了低于分辨率的微裂纹萌生，并对裂纹扩展和加宽后的方向与形貌进行了准确探测。

通过对图片进行判别，发现在载荷4 下试件出现裂纹，裂纹处于试件边缘位置，为便于理解，图8a中给出了在slice100上裂纹的大概位置（图8a 中黄框处）。为了研究DVC 方法在裂纹识别中的有效性，在裂纹尖端附近选择一个大小为40 voxel×80 voxel×60 voxel 的计算区域（图8a中红框处）。该计算区域如图8b 所示，x坐标的范围为［450，490］，y坐标的范围为［300，380］，z坐标的范围为［70，130］。采用DVC 分析时子 体 块 尺 寸 为21 voxel×21 voxel×21 voxel，步 长 为2 voxel，其他设置与前文一致。图8c 给出了该计算区域内的ZNCC 系数分布图，由图8c 可知，在裂纹附近，ZNCC 系数普遍偏低，这主要是由于在裂纹附近试件发生较大的变形，从而引起匹配失效。在CT 体图像分辨率不足的位置，明显可见ZNCC 系数局部化，即通过DVC 计算的ZNCC 系数分布图，可以简单、高效地判定亚体素微裂纹位置在试件内部的分布。

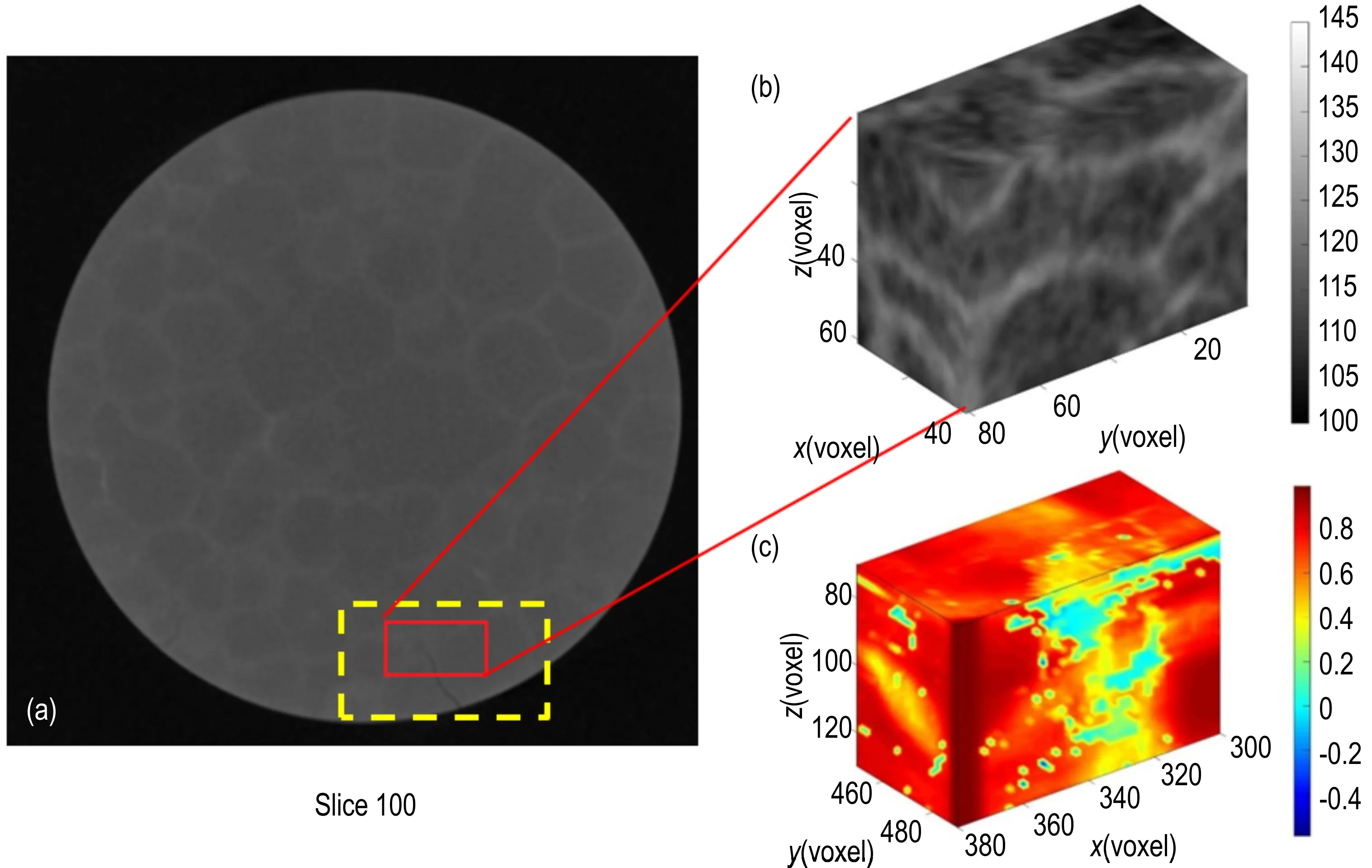
图8 基于DVC 计算ZNCC 系数分布的内部微裂纹分析：（a）边缘开裂的CT 灰度切片图，（b）裂纹尖端的红框区域体图像，（c）红框区域内的ZNCC 系数分布图Fig.8 Internal microcrack detection based on the distribution of ZNCC coefficient from DVC calculation：（a）a slice image of sample with a crack initiated from edge ，（b）CT image of crack tip region indicated by red box，（c）distribution of ZNCC coefficient of crack tip region indicated by red box

3 结论

在TATB 基PBX 材料单轴压缩实验中，通过DVC方法分析不同载荷下试件三维体图像，获得了加载过程试件内部变形场的演化情况。研究结果表明：

（1）在DVC 计算前对原始图像进行灰度直方图拉伸，经体图像优化，材料在4 种载荷下的ZNCC 系数均值在0.75 以上，DVC 计算结果具有较高的可靠性。

（2）压缩过程中随着载荷的增加，试件发生较大的压缩变形，断裂前达到了0.8%压缩应变。但是由于试件的颗粒体系的材料不均匀性，使其内部三维变形场也呈现出一定的不均匀性。

（3）将ZNCC 系数分布图应用于试件内部微裂纹的识别，能够简单、高效地确定小于μ-CT 尺度的微裂纹分布情况。