基于卷积神经网络的重力异常反演

李雅雯， 刘彩云*， 熊杰， 刘倩

(1. 长江大学信息与数学学院， 荆州 434023； 2.长江大学电子信息学院， 荆州 434023)

重力勘探是根据地球重力场研究地球构造及寻找矿产资源的一种地球物理勘探方法，重力异常反演是其中非常重要的一个环节。重力异常反演的方法主要分为两类：线性迭代反演和非线性反演。梯度下降法是十分流行的一种线性迭代方法，具有良好的稳定性和较快的收敛速度，但反演结果容易陷入局部最优解，并且计算耗时耗内存。模拟退火算法(simulated annealing,SA)、遗传算法(genetic algorithm,GA)和早期神经网络(neural network,NN)[1-3]是常见的非线性方法，有效解决了线性迭代方法容易陷入局部最优解的不足。随着生命科学与其他学科的融合发展，粒子群优化(particle swarm optimization,PSO)、蚁群优化(ant colony algorithm,ACO)和差分进化(differential evolution,DE)[4-7]，这类群智能算法也成功应用于解决地球物理反演中。

深度学习[8]是一种能够对高维数据进行不同层次地自动抽象，刻画数据本质的方法[9]。深度学习主要用来解决工程问题，在目标检测、图像分类和自然语言处理等领域[10]取得了关键性的突破。近年来，深度学习在地震数据和电磁数据的处理与解释中得到了初步的应用[11-14]。卷积神经网络(convolutional neural network，CNN)[15]作为一种经典的深度学习方法，被成功地应用于地震数据去噪、地震散射波场反演、航空电磁反演等领域，如高有湖等[16]成功证明了CNN能够有效提取地震勘探数据中的噪声信息；奚先等[17]提出了一种散射波场的CNN深度学习反演成像方法，可以辨识出测试模型中各散射点的准确位置，从全新的视角分析处理复杂的波场；Kyubo等[18]应用CNN从不同传感器高度的航空电磁数据中重建一维电阻率结构，发现CNN能在更短的周期内更准确地重建地下结构；陈冠宇等[19]将CNN应用于不良地质体的识别和分类中，发现当训练样本足够大时，能够十分精确分类不良地质体。

尽管CNN在地震和电磁勘探等领域取得了较大的进展，但很少应用到重磁勘探领域。现使用CNN解决重力异常反演问题，利用CNN建立地表观测重力异常数据到地下密度模型之间的映射关系，从而实现重力异常反演。

1 重力异常反演基本理论

1.1 重力异常正反演关系

重力异常是由地表到深部所有密度不均匀引起的重力效应的总和。重力异常正演是给定地下某种地质体的形状、剩余密度等，通过理论计算求取它在地面上引起的重力异常值的过程。重力异常反演则是依据地表观测的重力异常值推断出地下介质密度分布的过程。从数学角度来看，将地表观测数据抽象为数据空间，将反演出的地下介质密度分布抽象成模型空间。反演过程可以描述为数据空间到模型空间的一种映射关系，可以看成是正演过程的一个逆过程[17](图1)。

图1 正反演过程关系图Fig.1 Relation diagram of forward and inversion process

1.2 重力异常正演

“点元法”[18]是计算重力异常正演的常用方法，通常做法是将地下观测区域剖分成若干个规则正方形或矩形[图2(a)]。

每一个正方形或矩形看成一个点元，然后计算每一个点元对观测点的重力异常[图2(b) ]，再将所有点元对观测点的重力异常叠加求和，即为地下观测区域整个异常体对观测点的重力异常。

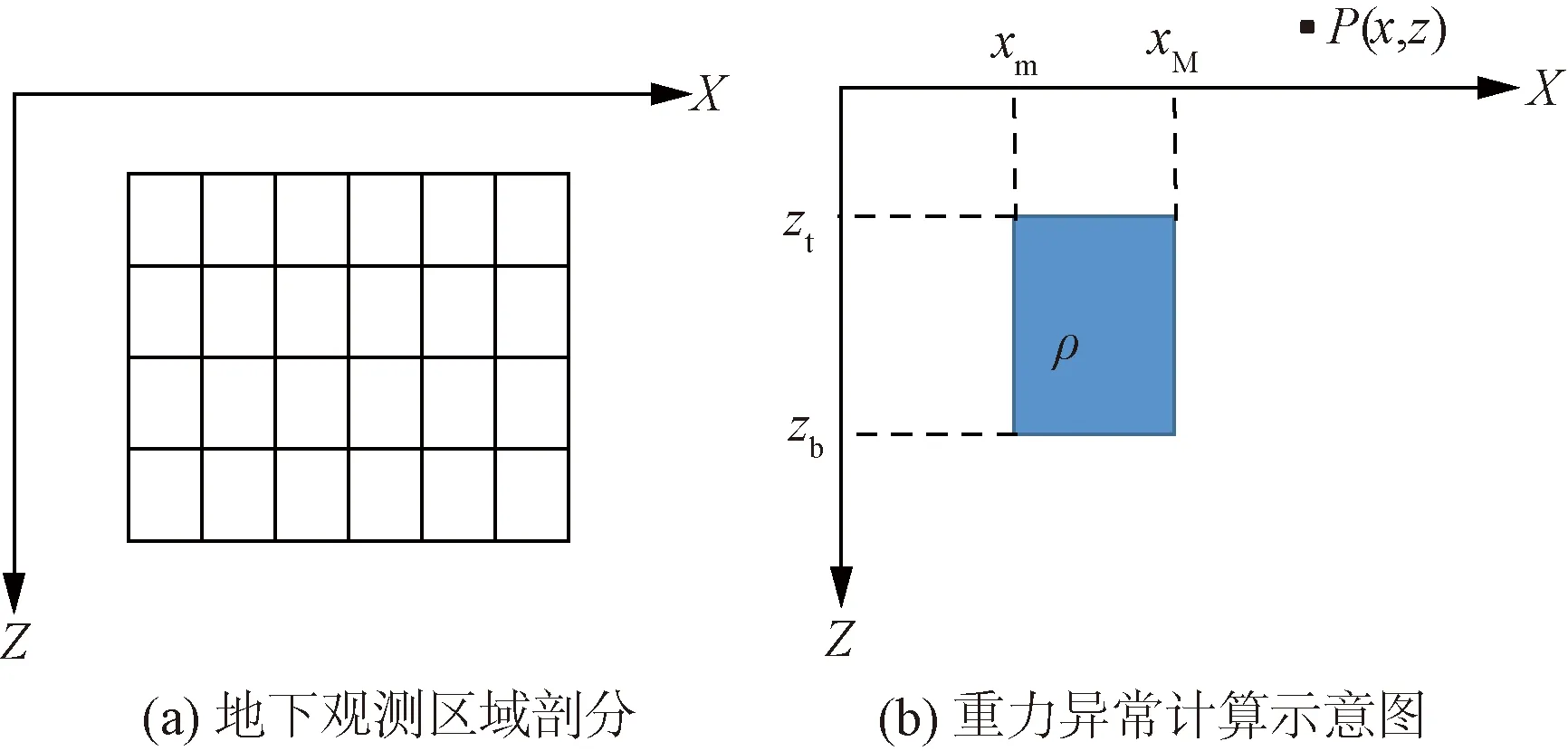
图2 地下观测区域剖分单元示意图Fig.2 Schematic diagram of the subdivision unit of the underground observation area

单个点元对于观测点P(x,z)的重力异常正演计算公式[19]为

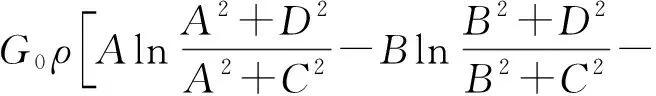
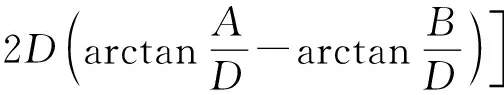
(1)

式(1)中：ρ为该点元的密度；G0为万有引力常量；A=x-xm；B=x-xM；C=z-zt；D=z-zb，xm、xM、zt、zb分别为点元四个顶点到X轴和Z轴的距离。

如果这些矩形点元足够小并且每个点元内部的密度固定不变，运用重力异常叠加原理，那么任意形状的地质体在观测区域产生的重力异常可以通过对构成这个形状的所有点元在观测区域产生的重力异常叠加来获取。因此重力异常正演可以表示为

d=Gm

(2)

式(2)中：m为地下密度模型，m=(m1,m2,…,mN)T,mi(i∈N)表示第i个网格的密度情况；d表示地表观测重力异常数据d=(d1,d2,…,dM)T,dj(j∈M)表示地表第j个观测点的重力异常值；G为M×N维核矩阵，表示单位点元对观测面产生的重力异常，计算方法参考式(1)，M和N分别为地表观测点数和地下网格剖分数。

1.3 重力异常反演

在地球物理工作中，通常能够获得的信息大多源于地表观测，仅有极少信息来自于地下空间(测井等)。因此，利用地表观测数据推断地下结构是地球物理勘探中一个十分重要的环节。重力异常反演就是依据地表观测的重力异常数据推断地下密度模型的过程(图3)。

图3 重力异常反演过程Fig.3 Gravity anomaly inversion process

(3)

2 基于卷积神经网络的重力异常反演

2.1 卷积神经网络(CNN)

卷积神经网络(CNN)是一种模仿生物视觉识别过程的人工神经网络[15]，具有参数共享、稀疏交互和等效表示等优点。CNN的常规结构是“卷积-池化-全连接”。在卷积神经网络中，一个卷积层包含多个卷积核，假设输入为M×N的图像，用x表示；卷积核大小为m×n，用w表示，偏置为b。卷积后结果中的每一个元素就是图形中对应卷积核大小区域与卷积核进行内积运算加上偏置得到的，即

h=g(x*w+b)

(4)

为了对卷积层提取的图像不同频段的特征进行抽样，在每一个卷积层后都紧跟一个池化层。池化操作主要有两种：平均池化和最大池化，其数学表达式分别为

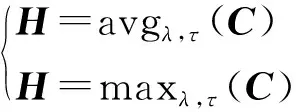
(5)

式(5)中：C表示经过卷积操作后提取的图像特征；λ、τ表示池化核大小为λ×τ。

经过多层卷积池化操作后，通过全连接层对抽象出的高级特征进行分类，即

O=f(W*X+b)

(6)

式(6)中：W为全连接层权重；X为卷积池化的输出转化为向量后作为全连接层的输入；b为全连接层的偏置；f(·)为全连接层所使用的激活函数。

2.2 卷积神经网络反演原理及方法

2.2.1 卷积神经网络(CNN)反演原理

基于CNN的重力异常反演与传统反演方法不同，它是通过最小化地下密度模型约束构成目标函数来实现[20]，即

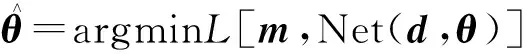
将无人机航拍技术与3D实景建模相结合，精准高效地完成项目场地地表建模工作[3]，使道路深化设计、结构分析计算、附属设计、管线综合以及管廊全专业实现三维协同设计。管廊全专业三维协同设计如图4所示。

(7)

图4分别显示了基于CNN重力异常反演网络训练流程图和基于CNN的重力异常反演示意图，通过利用地表观测的重力异常数据来预测地下密度模型况。首先，设计大量地下密度模型构成集合M={m1,m2,…,mk}，通过正演计算(d=Gm)得到对应的地表观测重力异常数据集合D={d1,d2,…,dk}[图4(b)①]。然后，将地表观测重力异常数据作为网络的训练输入，对应的地下密度模型作为网络输出的标签。有了足够的d和m来连续训练网络，就能够大致建立起由d到m的非线性映射。当达到最大迭代次数时，网络停止训练[图4(b)②]。最后，将实测地表观测重力异常数据输入到训练好的网络中，可直接得到地下密度模型[图4(b)③]。

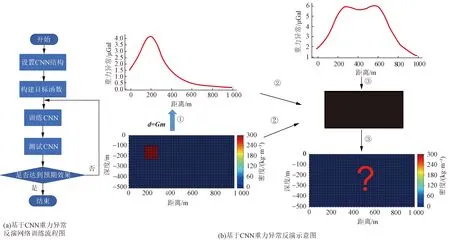
图4 CNN反演流程图及示意图Fig.4 CNN inversion flow chart and schematic diagram

2.2.2 网络结构

在本文研究中采用一维的CNN架构来实现重力异常反演。通过对比多次尝试得到的反演结果，以及参考其他反演的网络架构[20]，最终确定了图5所示的一维CNN结构。根据观测点和所剖分的地下空间，网络的输入层包含101个神经元，输出层包含800个神经元。中间包括三种类型：卷积层(CONV)，最大池化层(POOL)和全连接层。共有4个卷积层，每个卷积层后都紧接一个池化层。最后一个隐藏层是包含1 600个神经元的全连接层，此层全连接层的输入是将最后一个卷积池化层的输出矩阵展平得到。具体的，四个卷积层卷积核大小依次为1×5、1×4、1×3、1×3，步长均为1，通道数依次为10、20、40、80；所有最大池化层池化核大小为1×2，步长为1。

图5 一维的CNN结构Fig.5 One-dimensional CNN structure

2.2.3 网络参数设置

1)激活函数

神经网络是用于建立数据之间的映射关系。没有激活函数时，无论网络有多少层，输出都是输入的线性组合。激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到更多的非线性模型中，可以使神经网络适合任何复杂的函数。因此，选择合适的激活功能尤为重要，它可以加速网络的收敛，并显示出良好的训练效果。考虑到ReLU激活函数具有较好的快速收敛和深度传播优点，本文选择ReLU函数作为激活函数。

2)L2正则化和Dropout

深度学习中过拟合是普遍容易出现的一个问题。过拟合会导致拟合的函数完美预测训练集，但对新数据的测试集预测结果差。过拟合的实质是过度的拟合了训练数据，而没有考虑到网络的泛化能力。通过阶梯型模型对CNN网络进行了测试如图6(a)，发现反演结果非常差，阶梯型模型的边界、形状以及密度均没有很好的恢复。并且反演的形状类似于参与训练的某些训练样本，说明网络出现过度拟合。因此本文采用L2正则化和Dropout的方法，解决过度拟合这一问题。

L2正则化和dropout是通常用来改善过度拟合的常用方法。L2正则化是通过向损失函数中添加权重范数惩罚来限制网络的学习能力。为了能够使网络更加全面的学习，在构造损失函数时，加入了真实的地表观测重力异常数据d与网络预测地下密度模型正演得到的理论重力异常d′之间均方误差。完善后的损失函数为

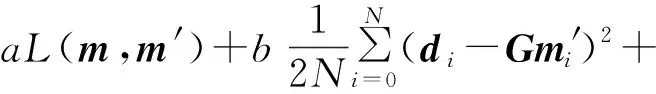
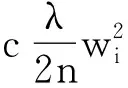
(8)

式(8)中：λ为控制惩罚项特定权重的正则化参数；a、b、c分别为地下密度模型约束项、数据约束项和权重约束项的系数，目的是通过调整不同约束项的系数，控制各约束项的权重，使网络能够充分学习地表观测重力异常数据与地下密度模型的关系，提高网络反演效果。Dropout技术的主要思想是在网络训练过程中以一定的概率随机的“关闭”神经网络的某些神经元。Dropout能够有效减少神经元之间复杂的共适应性，增强网络的泛化能力[21]。本文中在CNN的最后一层全连接层中加入Dropout。

图6(a)为不添加L2正则化和Dropout的阶梯型重模型反演效果，图6(b)为添加了L2正则化(λ=1)和dropout(最后隐藏层中每次只有90%的神经元参与训练)的阶梯型模型的反演效果。对比发现，添加L2正则化和Dropout后反演效果得到了很大的提升，不仅样本的形状、深度、边界和密度都与真实效果(白框)非常接近，还很好地反映出了模型的阶梯状特点。

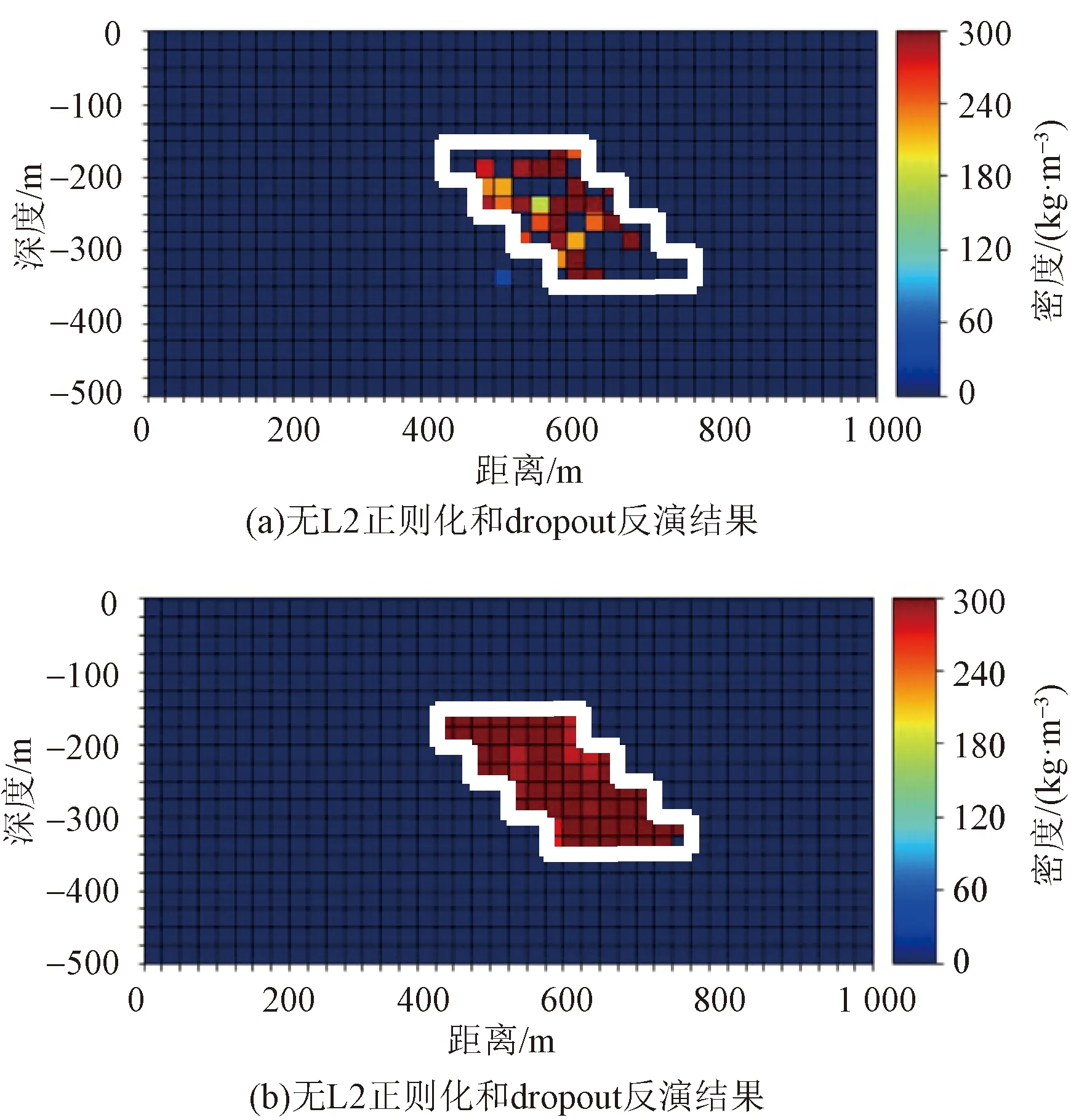
图6 是否添加L2正则化和dropout反演结果对比Fig.6 Whether to add L2 regularization and dropout inversion results comparison

3)迭代次数

损失函数下降曲线如图7所示，通过观察三条损失曲线，在45 000次迭代后，总误差、地下介质密度分布约束误差和数据约束误差的下降趋势已趋于平稳，因此本文选择50 000次作为网络训练的迭代次数。

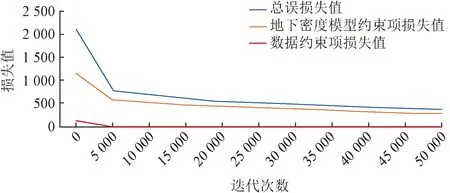
图7 损失函数下降曲线Fig.7 Loss function declining curve

3 模型实验与结果分析

3.1 数据集的生成

深度学习是一种有监督的学习方法，通过大量的数据训练，使网络能够有效解决问题。例如，Hu等[20]生成了数千组随机2D磁异常模型来训练CNN；Yang等[22]生成了1 730组速度样本进行地震速度模拟。在设置训练集样本[20]时，将观测地下空间划分为800个(20行×40列)矩形单元格，每个单元格大小为25 m×25 m。在正演中，将地面观测点设置为101个，观测点之间的间距为10 m。数据样本包含不同大小、形状(正方形、矩形)和位置的重力异常体，如3×3(75 m×75 m) 、4×4(100 m×100 m) 、 5×5(125 m×125 m)、3×6(75 m×150 m)、6×3(150 m×75 m)、4×8(100 m×200 m)、8×4(200 m×100 m)。为防止边缘数据对试验的误差影响，舍弃靠近地下网格边缘2个单元部分的数据，只保留中间部分的数据。由于从密度到重力异常的关系是线性的，网络很容易学习这种线性关系，因此仅将重力异常体的密度设置两种不同的值(200 kg/m3和300 kg/m3)。通过重力异常正演生成了5 542组地下密度模型及其对应的地表观测重力异常数据，图8显示了数据集中的6个代表性示例。

图8 数据集中6种代表性地下密度模型Fig.8 Six representative underground density models in the data set

3.2 测试集模型反演

从5 542组样本数据中随机抽取80%作为训练集，20%作为测试集，反演参数设置如表1所示。

表1 CNN反演参数设置Table 1 CNN inversion parameter settings

图9显示了测试集测试部分样本的反演结果，用不同的颜色表示不同的密度，用白框显示模型的真实位置，蓝色的虚线表示实际重力异常，红色实线表示预测的地下密度模型正演得到的理论重力异常。通过观察发现，一些重力异常体的个别位置预测密度低于实际值，并且四周存在少量的不集中的异常信息，但不影响确定重力异常体的中心位置和整体形状。

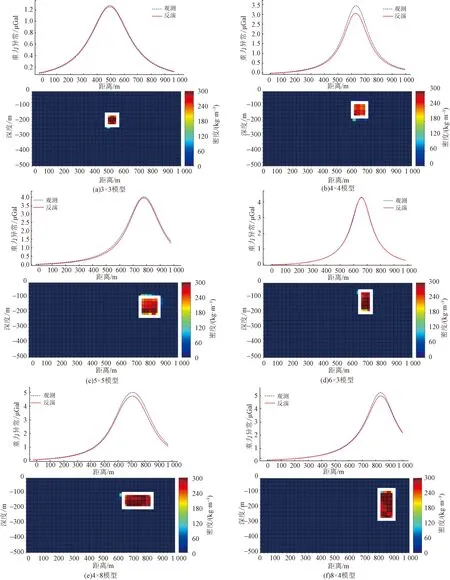
图9 测试集反演结果Fig.9 Test set inversion result

3.3 验证集模型反演

由于训练集和测试集均是从样本数据中提取的，训练集和测试集之间存在一定的相似性。因此测试集的反演结果只能评估学习的效果，无法评估网络的泛化能力。因此设计了几种与训练数据集模型差异很大的地下密度模型构成验证集(图10白框所示)，来检验训练好网络的泛化能力。

图10显示了验证集中6种样本数据反演结果。结果显示，对于单一复杂模型图10(a)、图10(b)，CNN能够很好地恢复出其形状、深度、边界和密度，并且很好地恢复出了阶梯型模型每一层之间的阶梯特性；对于组合模型，CNN很好地推断出左右结构组合模型[图10(c)～图10(e)]的物理性质，几乎与真实结果完全一致。在重力异常反演中，由于浅层的强异常抑制了深层的弱异常，导致CNN对深层异常的学习不敏感，因此反演结果的垂直性能不如水平性能好，如图10(f)深部模型轻微倾向于与浅层模型体相连，但与真实模型也十分接近。

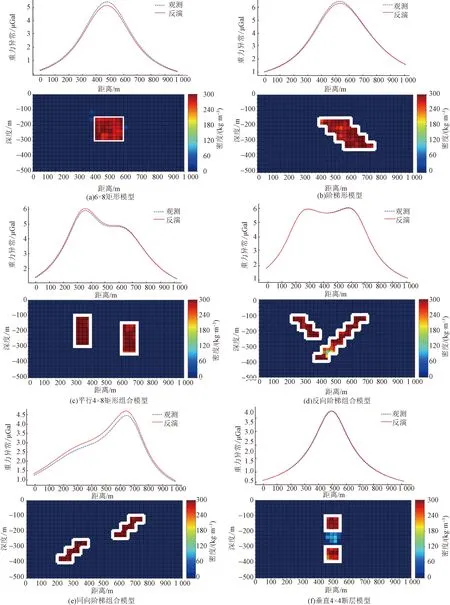
图10 验证集模型反演效果Fig.10 Verification of the set-type inversion effect

通过测试集和验证集模型反演结果可看出，本文提出的CNN重力反演方法能有效解决重力异常反演问题，且具备很好的泛化能力。与传统的重力异常反演方法相比，该方法也很好地解决了反演结果分辨率不高、模型特征不明确以及边界不清晰的问题。

4 结论

提出了一种基于CNN的重力异常反演方法，该方法首先构造了包含4层卷积池化层和1层全连接层的卷积神经网络；然后通过大量正演计算得到训练数据集并训练该卷积神经网络，训练中采用Relu激活函数、Adam优化器、采用L2正则化和Dropout防止网络过拟合，并优选目标函数各约束项权重系数；最后将重力异常数据输入训练好的卷积神经网络得到反演结果(地下密度模型)。实验结果表明，该方法能快速、准确地反演出地下密度模型的物理性质，泛化能力强，可有效解决重力异常反演问题。CNN是一种高级的网络结构，擅长提取空间信息，但对于一维观测数据，这种优势不明显，在未来可尝试用CNN或其他深度学习的方法解决3D重力异常反演问题。