乌江中上游地区极端降水特征及未来预估

冯椰林， 焦树林， 贺中华， 杨柳英

(贵州师范大学 地理与环境科学学院， 贵州 贵阳 550025)

1 研究背景

近些年来，极端降水事件愈加频繁，其强度也呈现出显著增大的趋势[1]。极端降水事件频率、持续时间及强度的提升对地区经济，尤其是对气候变化较为敏感与脆弱地区的生产生活及社会的可持续发展形成了严峻的挑战[2-3]。流域地区在面对极端气候时，相较于其他地区更具脆弱性。在全球气候日渐极端化的背景下，流域地区如何提高气候灾害的防范和控制力成为地区可持续发展的重要议题。

河流水量补给主要来自于降水，降水的多寡不仅决定着河流流量的大小，也决定着流域整体的水循环过程[4]。针对流域地区的极端降水，不同学者从不同角度开展了研究。高佳佳等[5]利用广义帕累托分布(generalized pareto distribution, GPD)函数、重现期计算、Hill图等方法对雅鲁藏布江进行极端降水模拟后发现，中上游流域地区未来发生破纪录的极端降水事件的概率较大；祝莹等[6]对沱江流域近67年的7个极端降水指标进行研究后发现，其流域内的极端降水事件总体上呈减少趋势，但是在极端日数指标上趋势不明显；赵爱莉等[7]对汉江流域陕西段1971-2018年的极端降水时空特征进行研究后发现，6个指标中有5个都呈下降的状态，汛期降水与年降水具有一致性，预计未来汉江流域的极端降水事件会增多。对未来降水进行预估，可对灾害进行预先防范。目前对降水预估的方式较多，短期预估的方法有马尔科夫法[8-9]、网络神经法等[10]，但是在对长时间序列进行预估时，大多数学者倾向于使用全球气候模式(global climate models，GCMs)[11]。

国际耦合模式比较计划(Coupled Model Inter-comparison Project，CMIP)已经发展到了第六阶段。来自全球30多个机构参与其中，各机构在CMIP总框架下，通过建立理想化的实验场，开发出了各种实验结果[12]。CMIP6计划相对于CMIP5，除了实验的动力参数和模式分辨率不同外，CMIP6在情景比较模式中还增加了共享经济路径(share socioeconominc pathways，SSPs)[13]，以期更好地反映当前社会发展的情景状态。利用CMIP6对中国气候进行的研究已经取得了一定的进展，李晓蕾等[14]利用13个GCMs下的4个SSPs情景数据预估了长江流域未来降水变化；赵梦霞等[15]选择了5个GCMs下的7个SSPs情景对黄河上游地区进行了模拟，结果表明，模式数据能够表征黄河流域的降水空间特征，不同情景下降水均呈增多趋势，不同年份的趋势幅度有所区别；黄晓远等[16]在对中国西南部极端降水进行预估后，认为西南地区未来极端降水将会加剧，建议加强防范。

乌江流域中上游地区是贵州省和重庆市人口密度大、商业发展较迅速地区，流域内的气候问题关乎两省(市)发展的可持续性。本研究基于乌江流域中上游16个气象站点实测降水资料与CMIP6资料，揭示该流域历史极端降水与未来降水规律，可为地区的灾害防范提供参考。

2 数据来源与研究方法

2.1 研究区概况

本研究区乌江中上游地区介于104°E～109°E、26°N～29.5°N之间，绝大部分处于贵州省境内。研究区内河流支流众多、河网密布，以降水补给为主。气候以亚热带季风气候为主，雨热同期，流域生态保护较好，两岸植被茂密，水质良好，常年呈深绿色。研究区地势由西南方向逐渐向东北方向放缓，与河流走向具有一致性，地势最高处位于赫章县附近，最低处位于沿河地区。整个流域的中上游地区为贵州省经济发达、人口密集区域，贵阳市、遵义市、毕节市等工商业较发达的城市均位于流域内。乌江流域的发展对于整个贵州省的发展至关重要。乌江流域中上游地区水系、高程及气象站点分布如图1所示。

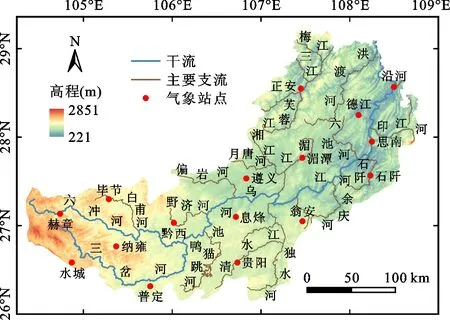
图1 乌江流域中上游地区水系、高程及气象站点分布

2.2 数据来源

本研究的第1部分数据来源于国家气象局，挑选了乌江中上游流域16个气象站点(其位置见图1)的实测资料，数据经过严格质量把控，时间尺度为1961-2019年。第2部分的预估数据来源于CMIP6下5个GCMs(https://esgf-node.llnl.gov/projects/cmip6/)，选择了3种未来情景，分别记作SSP126、SSP245、SSP585，设置历史时期为1975-2014年，未来时期为2020-2100年，共80 a，将5个GCMs进行集合平均(multi-model ensemble, MME)后进行预估。5个GCMs的详细信息见表1。由于所选的5个GCMs的分辨率不一致，为了便于研究，将其通过双线性插值法重采样到0.5°×0.5°后，再进行集合平均[17-18]。

2.3 研究方法

2.3.1 极端降水指数定义 本研究依据世界气象组织发布的27种极端气象指数，经综合考虑，选取了CDD、R99P、RX1、RX5、R50mm共5种表征极端降水的指数[19]，各指数的定义及单位见表2。其中，CDD也可以表征干旱情况。

表1 选取的5个GCMs详细信息

表2 5个极端降水指数的定义及单位

2.3.2 Morlet小波分析与EOF分解 小波分析方法和经验正交分解法(empirical orthogonal function，EOF)已在水文要素领域被广泛运用。两者运用各自原理可以揭示要素的多种时空特征，小波分析主要揭示要素变化的周期性，EOF主要揭示要素的空间一致性，同时两者还可以对要素演变在时间维度上进行表征[20-21]。

2.3.3 QM降尺度法 CMIP6的原始分辨率较低，在中小尺度区域研究时容易造成误差，所以有必要对其进行降尺度处理[22]。QM(quantile mapping)方法考虑了经验累积分布函数来进行偏差订正，而不是采用简单的理论分布函数[23]，依据实测日数据的累计分布形状，来对GCMs日数据进行修正，此方法能够较好地修正出日降水事件的极端性，特别是R50mm、R99P这种异常极端降水事件。计算公式如下:

Prm,r=ecdfm,r(Pm,r)

(1)

CFm,r=ecdfo-1(Prm,r)-ecdfm,r-1(Prm,r)

(2)

(3)

Pc,f=Pm,f+CFm,f

(4)

式中：Prm,r为计算的模式数据率定期经验分布概率；Pm,r为模式数据的日降雨量；CFm,r为公式(1)结果上实测与模式数据的经验累积反函数在率定期的偏差因子，利用CFm,r可以外推或插值得到CFm,f公式(3)；Pc,f为修正后的模式未来时期逐日降水量；其中，下标r和f分别表示率定期(本文为1975-2014年)和预估期，下标o和m表示实测和模式降水数据。本研究将站点实测资料作为观察资料来进行偏差订正。

3 结果与分析

3.1 极端降水指数时空变化

研究区5个极端降水指数变化趋势空间分布见图2。由图2可见，CDD呈不均匀分布，高增长趋势的区域集中在研究区西部，东北部减少趋势最为显著，而其余4个指数的变化趋势分布与CDD相反，在空间上均呈四周为增大趋势、中部为减小趋势的态势。变化趋势最大的为R99P，其增大趋势的最大值达到了11.6 mm/10a。总的来看，5个指标在研究区的西部高海拔区、中北部、东南部及东北部均呈增大趋势，其余地区则为减小或不变，在空间上极具一致性。

1961-2019年研究区5个极端降水指数年际变化趋势见图3。由图3可以看出，在时间变化上，CDD、RX5为减小趋势，但两者的变化率非常微小，分别为-0.021 d/10a和-0.066 mm/10a；R99P、RX1和R50mm均为增大趋势，变化率分别为4.573 mm/10a、0.820 d/10a和0.079 d/10a。1961-2019年间，CDD最大值出现在1969年，其他4个指标的最大值均出现在2014年。从实际来看，2014年整个研究区降水量异常增多，属于特涝年，贵州省各地均有洪涝灾害发生。

3.2 极端降水指数周期变化

通过小波函数计算得到小波实部后，再对各极端降水指数的小波实部进行可视化转换，可得到各指数空间和时间维度上的周期规律，图4为1961-2019年研究区5个极端降水指数的小波变化。

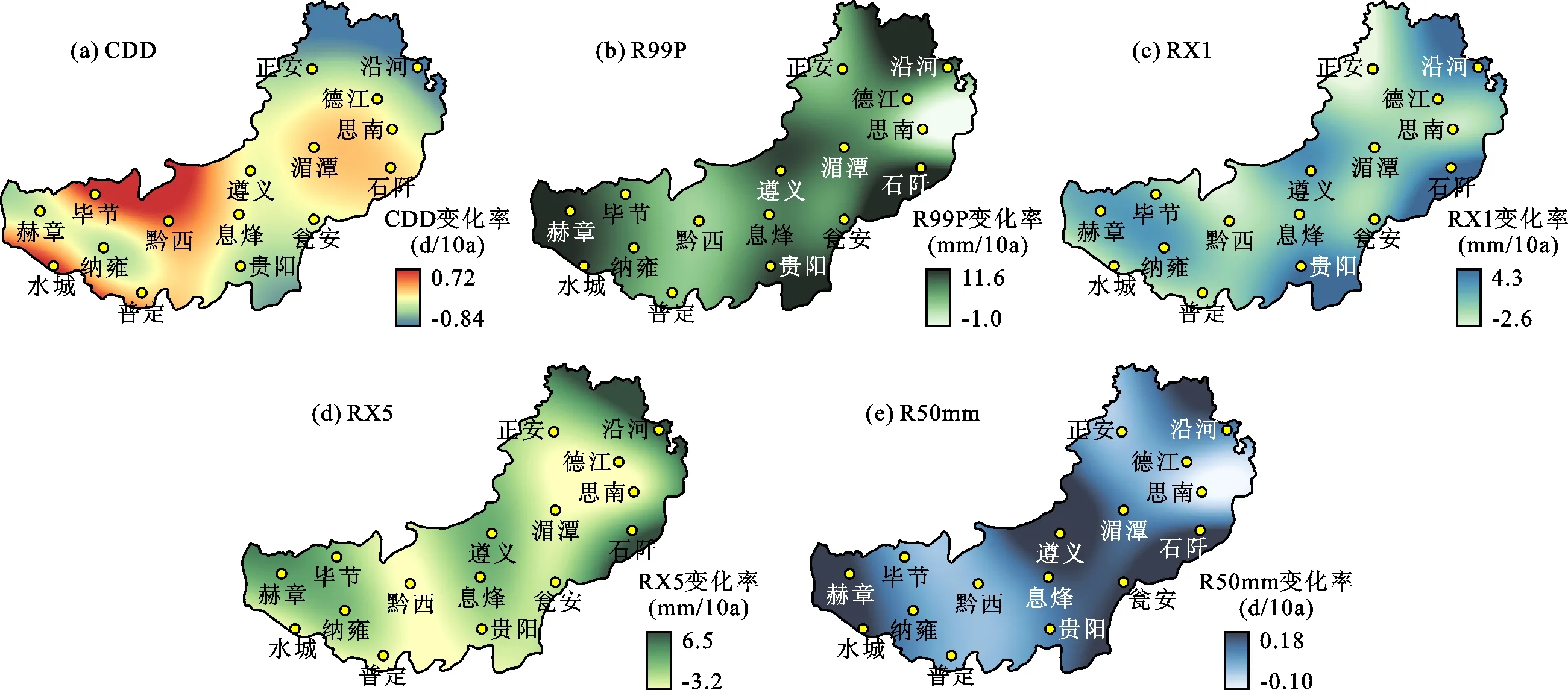
图2 1961-2019年研究区5个极端降水指数变化趋势空间分布

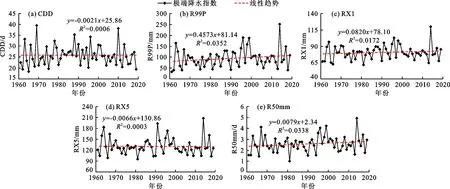
图3 1961-2019年研究区5个极端降水指数年际变化趋势

由图4可以看出，不同指数的周期规律及方差均存在差异。CDD的小波实部(图4(a))在10～15 a和23～30 a的时间尺度上信号较为强烈，高值出现在1960年，时间尺度为28～30 a，低值出现在1970和2013年，时间尺度为25～30 a；小波方差图(图4(b))显示，CDD存在3个周期变化，其中方差最大值相应的为28 a，也是CDD的第一周期，其余两个周期分别为6和15 a。R99P的小波实部(图4(c))在周期上主要为4～6 a和23～28 a尺度的变化，23～28 a周期十分明显，且贯彻整个时序，4～6 a尺度只在1976-2009年出现；R99P小波方差(图4(d))在6和26 a存在2个主要峰值，且以26 a为第一周期。RX1的小波实部(图4(e))存在5～9 a和25～30 a两个主要周期，且均具有全时序性；小波方差(图4(f))有3个主要峰值，对应的时间尺度分别为6、12和28 a，其中28 a为第一周期。RX5的小波实部(图4(g))主要存在25～30 a的周期，且贯彻整个时序，其他时间尺度的周期则不显著且不连续；RX5的小波方差(图4(h))有3个峰值，对应的时间尺度为6、12和28 a，且28 a为第一周期。R50mm存在23～30 a的显著周期(图4(i))，且具有连续性，周期规律十分明显，经历3.5个准震荡变化，其小波方差显示主要周期为6、9、27 a，27 a为第一周期。

3.3 极端降水指数空间向量特征分析

通过EOF分解对1961-2019年的各极端降水指数进行模态分解，在空间和时间维度上得出了相应结果，限于文章篇幅，仅选择了第1、第2模态的空间向量特征结果，如图5所示，为了便于区别空间差异，对图5中模态2的符号系统进行分类，以区别出正负区间。第1、第2模态的方差累积贡献率较大(表3)，且无重叠值，即表明通过North检验。由图5可以看出，5个指数的第1模态均为正值，表明5个指数在空间变化上具有一致性。各指数的第2模态则表现出一定的空间差异，CDD空间分异为东-西的格局；R99P的空间分异为西-其他型格局；RX1的空间分异为西、北、南-中、西北的格局；RX5的空间分异为中部、东、东南-北、西的格局；R50mm的空间分异格局为南-东北。第2模态仅考虑大致分异格局，不考虑某些地区的微小分异。

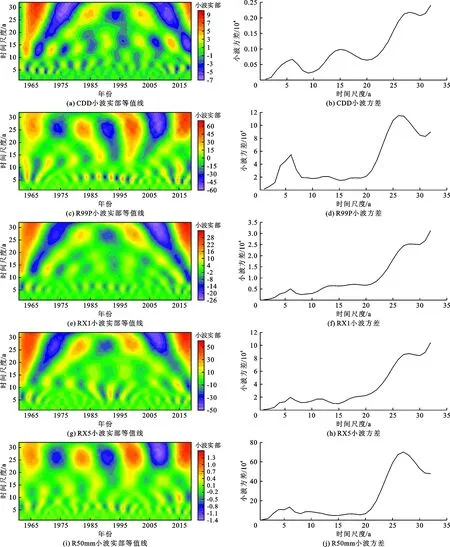
图4 1961-2019年研究区5个极端降水指数的小波变化

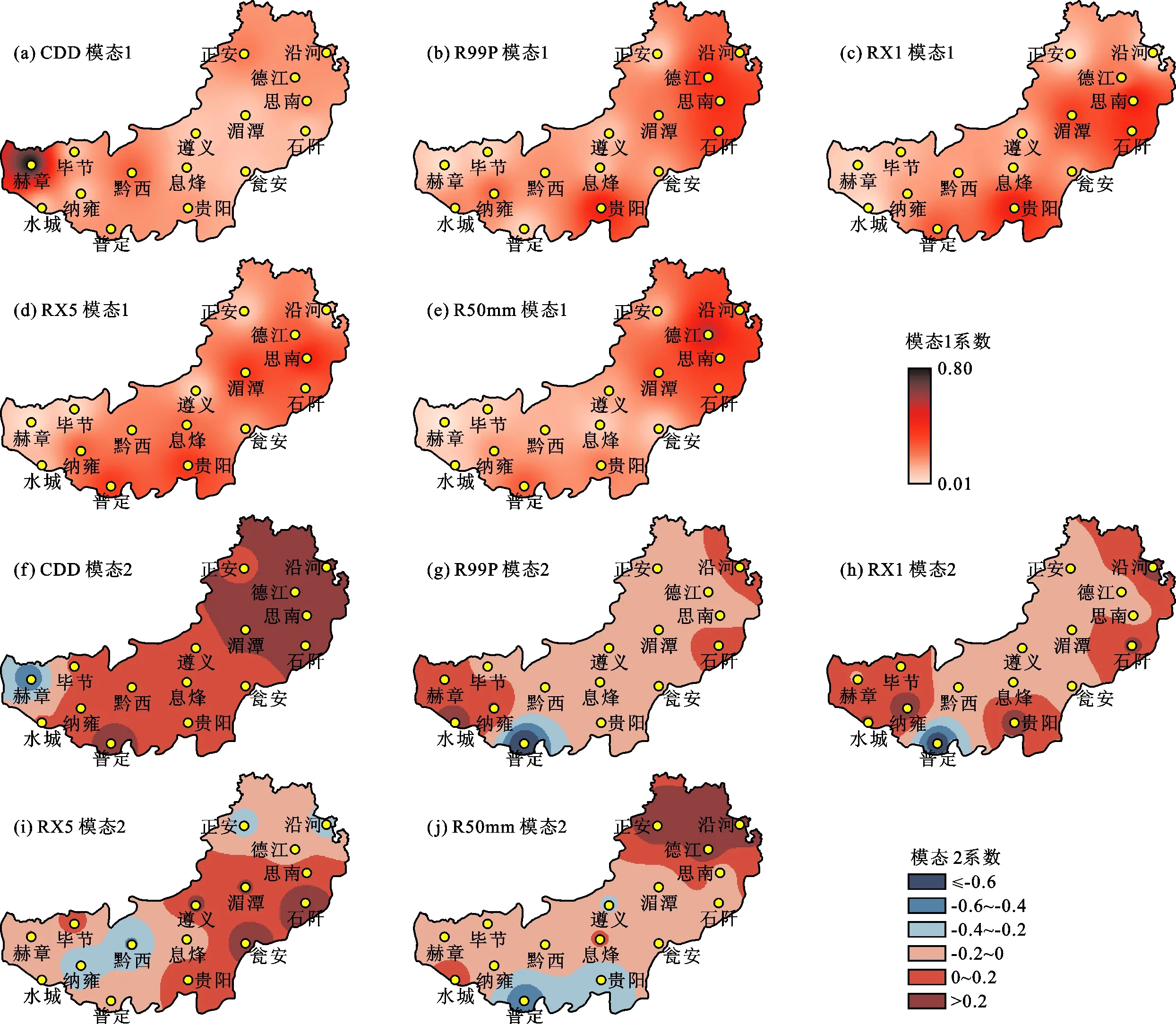
图5 研究区5个极端降水指数第1、第2模态空间向量特性

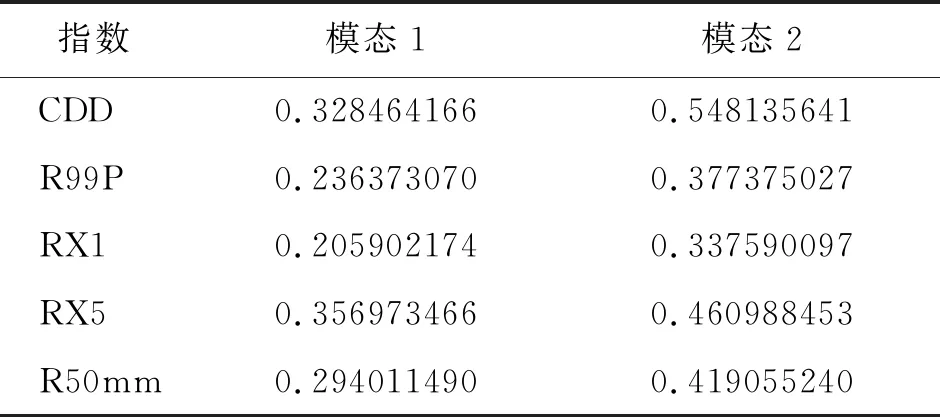
表3 第1、第2模态的方差累积贡献率

时间系数是空间模态的补充说明，正的时间系数与正的空间模态系数具有相关性，时间系数正负值影响模态的空间方向，且时间系数的绝对值决定其向量特征的典型度[24]。图6给出了5个极端降水指数第1、第2模态的时间系数。从图6中各极端降水指数在研究时段内各年份时间系数的大小来看，CDD模态1在1969、1974、1988、2013年的值较大，表明这些年份的空间特征为模态1，且在1969年最为典型；CDD模态2在1978、1982、1996、2000、2010年为主导，且2010年最为典型。R99P在1963、1996、1998、2014年为模态1主导，且2014年最为典型；在1979、1983、1991、1995年以模态2为主导，且1991年最为典型。RX1在1991、1996、1998、2014年以模态1为主导较明显，其中2014年最为典型；在1964、1979、2004、2005年以第2模态为主导较为明显，且1964年最为典型，但时间系数为负，表明研究区中部和西北部雨量多，其余地区少。RX5的第1模态的时间系数值波动较大，在1964、1981、1991、1996、2014年较为显著，其中2014年模态特征最为明显；模态2在1965、1980、2015、2016年为主导较为明显，2016年最为典型。R50mm第1模态主导较明显的年份出现在1967、1996、1999、2014年，且2014年最为明显；以第2模态为主导较明显的年份为1965、2008、2015、2016年，其中2015年最典型，但为负值。

综合来看，除CDD外，其余4个指数的第1模态绝对最大值均出现在2014年，这也验证了2014年降水量的异常性。由于CDD表征的是干旱程度，所以其时间系数与其他4个指数有所不同。

3.4 极端降水未来预估

3.4.1 降尺度评价 在进行未来极端降水预估研究前，首先对于降尺度的效果进行评价。1975-2014年5个极端降水指数及年降水量模式数据矫正前后与实测数据对比见图7，这些数据矫正前、后的多年平均值与实测值对比列于表4。由于在研究期CMIP6原始资料中发现，研究区的R50mm仅发生过2～3次，多年平均值接近于0，所以在图7和表4中对矫正前的R50mm值未作展示。

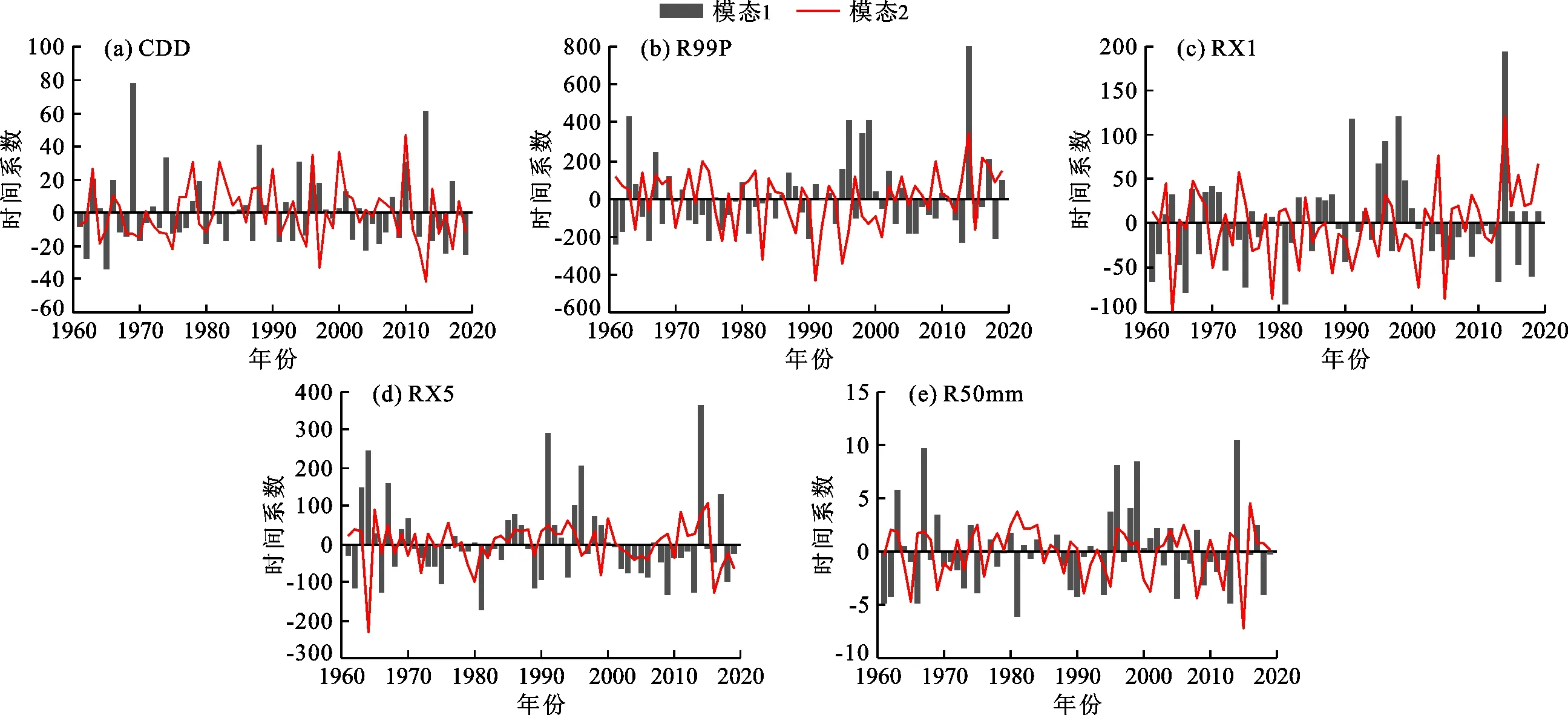
图6 1961-2019年研究区5个极端降水指数第1、第2模态时间系数

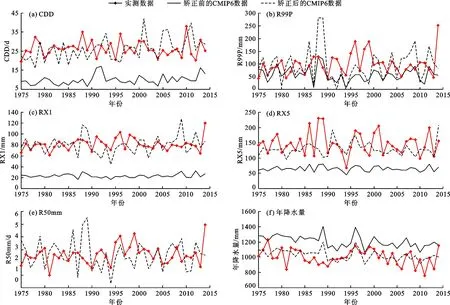
图7 1975-2014年5个极端降水指数及年降水量模式数据矫正前后与实测数据对比

图7表明，矫正前的模式数据严重低估了研究区的极端降水事件，各指数无论是数量级还是时序分布上，均与实测值存在较大差异，但是在经过降尺度处理后，模式数据接近于实测数据。另外，年降水量存在高估现象，这与CMIP6数据在日降水发生概率上雨日多但量值低的特征相关。总的来看，通过QM方法降尺度后的模式数据无论是量值还是时序分布上，均与实际值接近，可以用于后续研究。

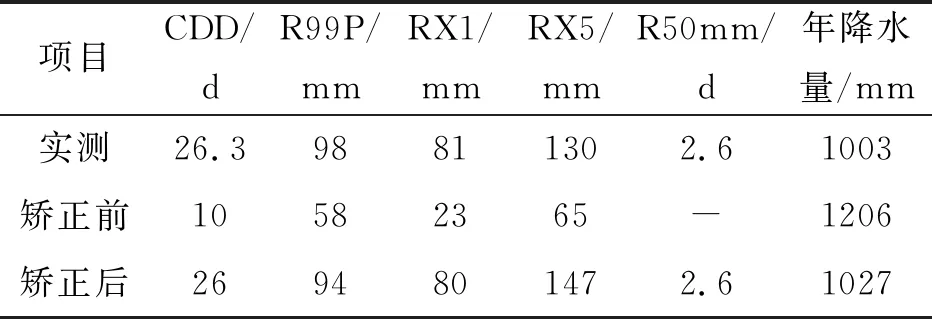
表4 极端降水指数及年降水量矫正前后均值对比(1975-2014年)

3.4.2 不同SSPs情境下极端降水指数空间变化 不同情景模式下极端降水指数在空间规律和量上均有差异，导致极端降水事件也相应有所不同。图8给出了SSP126、SSP245、SSP585 3种情景下，未来2020-2100年研究区5个极端降水指数及年降水量变化的空间趋势。

由图8可以发现，CDD在SSP126情景下，只有高海拔地区的赫章县呈增大趋势，倾向率为0.1 d/10a，其余地区则均为减少趋势，SSP245情景下整个研究区均为减少趋势，SSP585情景整体趋势倾向率最大，但部分地区呈增大趋势，贵阳地区尤为突出；R99P在3种情景下均为增大倾向，倾向率随情景依次增大，倾向率高值中心也随之由东北向西南转移，最高值在SSP585情景下的普定县(26.5 mm/10a)；RX1的倾向率高值区主要位于研究区东北部，随情景的升高而愈发明显，在SSP585情景下最为显著(6.6 mm/10a)；RX5的变化与RX1的变化具有相似性，3种情景下的倾向率高值区均位于东北部，但SSP126情景的高值却大于SSP245情景，倾向率极值出现在SSP585情景，达到了12.3 mm/10a；R50mm在SSP126情景下的水城区出现减少趋势，但范围不大，也不显著(-0.1 d/10a)，其余两个情景全研究区均为增多态势，倾向率最大值出现在SSP585情景下的普定县，达到了0.7 d/10a；3种情景下年降水量均为增大趋势，且整体上随SSP情景的升高而增大，倾向率高值由北向西南转移，在SSP585情景下普定地区的倾向率最高，为28 mm/10a，高海拔地区赫章县在3种情景下的年降水量变化始终最缓慢。总的来看，整个研究区无论是极端降水指数还是年降水量的倾向率均随着SSP情景的升高而趋于明显，普定县地区尤为显著，在未来的极端降水事件灾害防范中，应加强该地区的应对。

3.4.3 不同SSPs情景下极端降水指数时间变化 图9给出了SSP126、SSP245、SSP585 3种情景下，未来2020-2100年研究区5个极端降水指数及降水量的年际变化情况。

图9显示，3种情景下除CDD之外的其他4个极端降水指数在未来均表现为增大倾向，且整个趋势具有极强的显著性。CDD在3种情景下均为负倾向变化，且SSP126情景下的整体趋势最明显，倾向率达到-0.922 d/10a；R99P的波动较大，最低值为0，最高达到463 mm，倾向率在SSP585情景下最大，达到19.075 mm/10a，且增长最明显的时期发生在2070年后；RX1的波动较小，但也一直处于增大状态，其值维持在50～150 mm之间；RX5与RX1有着相似的变化趋势，只是量值范围有所扩大，SSP126和SSP245情景的倾向率大致相同，但是SSP585情景的倾向率约为前两个情景的2倍，达到9.57 mm/10a；R50mm与年降水量未来也均为增大趋势。另外，由图9可以发现，2070年后各极端降水指数(CDD除外)在3种情景下均发生突变性陡增，以SSP585情景最为突出。总的来看，除了CDD之外的其他4个指数在未来时期会不断增大，2070年之后趋势更为显著，因此2070年后极端降水事件会迎来一个高峰期，年降水量也是如此。

4 讨 论

本研究区乌江中上游地区虽然属于小尺度流域，但各极端降水指数的变化特征各异，总的来看，1961-2019年研究区极端降水事件整体呈增多趋势，但是未发生显著性的改变，这也验证了罗玉等[25]的研究结论。乌江流域中上游位于印度洋季风和东南季风交界地带，受两者影响巨大[26]。赫章县、威宁县等地由于地势较高，水汽难以到达，导致降水少，而流域东北和南部地区地势低，且南部背靠高原、东北部临近长江，导致普定县及研究区东北部成为极端降水事件多发区。

降尺度方法虽然在局部地区存在偏差，但可以最大限度地使模式数据接近于实际值，以便后续研究。在模拟过程中单一的CMIP6模式不可避免地会带来误差，而多模式集合的方式可以最大程度地降低这一影响，提升结果的可信度[27]。

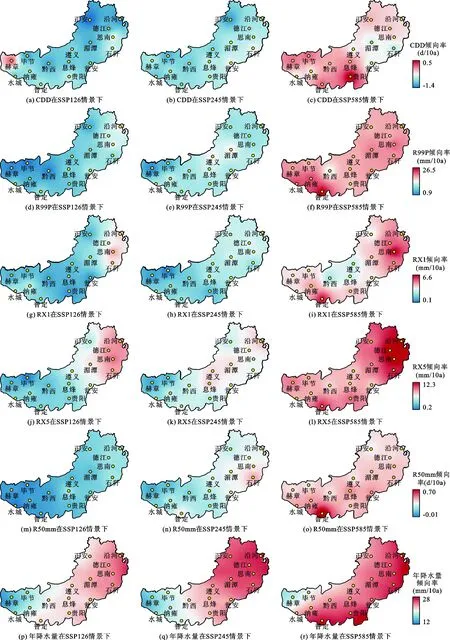
图8 3种情景下2020-2100年研究区5个极端降水指数及年降水量变化的空间趋势

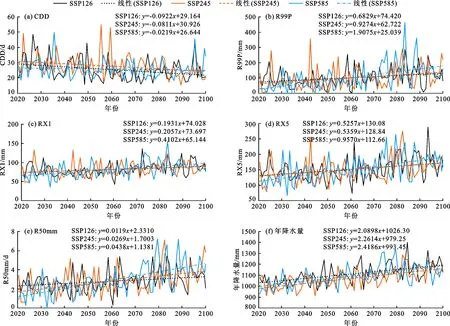
图9 3种情景下2020-2100年研究区5个极端降水指数及降水量年际变化

由于CMIP6的数据结构特性，对于不同的极端降水指数模拟会出现高估或低估的现象[28]。对于本文的研究区，CMIP6数据表现出降雨日多、中雨日多、但量值不大的特点，所以出现了对特极端降水事件低估、对年降水量高估的结果，且会对中极端降水事件(R25mm、R95P等)表现为高估的现象。简而言之，CMIP6原始降水在发生概率上缺乏特极端性，这是需要重点注意的。当然，研究区和模式数据选择的不同，情况可能也会有所不同。

不同的多模式集合方式也会对模拟精度产生影响，对于未来的研究应考虑多种集合方式(非等权集合、贝叶斯模型、遗传算法等)，从中择优选择。

5 结 论

本文对乌江流域中上游地区1961-2019年5个极端降水指数的时空变化特征进行了分析，并在降尺度处理后预估了未来2020-2100年极端降水指数及年降水量的变化，得出以下主要结论：

(1)在空间上，研究区5个极端降水指数变化趋势有增有减。CDD呈不均匀分布，高增长趋势的区域集中在研究区西部，东北部减少趋势最为显著，变化率约为-0.84 d/10a，而其余4个指数的变化趋势分布与CDD相反，在空间上均呈四周为增大趋势、中部为减小趋势的态势。在时间序列上，CDD和RX5为减小趋势，其余指数为增大趋势。

(2)小波分析结果显示，不同极端降水指数存在不同的周期特征。RX1与RX5的周期变化极其相似，均存在25～30 a时间尺度的主周期，且贯穿整个时序；CDD在10～15 a和23～30 a时间尺度上信号最强烈，方差在28 a时的值最大；R99P在23～28 a时间尺度上信号最强烈，26 a为第一周期；R50mm在23～30 a时间尺度上信号显著，且27 a为第一周期。

(3)EOF分解结果显示，5个极端降水指数在空间变化上具有一致性。第1模态的模态系数在0.01～0.80之间；第2模态则有着明显的空间分异性，模态系数有正有负。从时间系数上看，研究期内第1模态控制的年份较多，且较为典型。

(4)QM降尺度法对乌江流域具有良好的适用性。降尺度后的5个GCMs模式集合平均表明，在未来不同情景下，研究区极端降水事件和年降水量均显著增多，且在2070年即21世纪后期将会发生显著性突变。