WPT-HPO-ELM径流多步预报模型研究

许建伟， 崔东文

(1.云南省水利水电勘测设计研究院, 云南 昆明 650021； 2.云南省文山州水务局, 云南 文山 663000)

1 研究背景

径流时间序列预报，尤其是径流时间序列多步预报一直是水文预报研究的热点和难点。提高径流时间序列多步预报精度对于水文预报、水资源开发利用等具有重要意义。由于河川径流形成过程机理复杂，BP(back propagation)神经网络[1]、支持向量机(support vector machines，SVM)[2]、随机森林(random forest，RF)[3]、长短时记忆神经网络(long short-term memory networks, LSTM)[4]等传统预测方法难以获得满意的预报效果。目前，基于“分解-预测-集成”的智能预测混合方法被广泛应用于径流时间序列预测研究，如包苑村等[5]基于变分模态分解(variational mode decomposition，VMD)方法和卷积-长短期记忆神经网络(convolutional neural network and long short-term memory networks，CNN-LSTM)建立VMD-CNN-LSTM模型，通过渭河流域张家山站和魏家堡站1960-2005年实测月径流数据对模型进行验证，结果表明VMD-CNN-LSTM模型具有更优的预测精度以及更小的误差；席东洁等[6]基于经验模态分解(empirical mode decomposition，EMD)与Elman神经网络建立了EMD-Elman月径流组合预测模型，并将其应用于黄河上游唐乃亥水文站1979-2009年的月径流时间序列预测中；桑宇婷等[7]建立了互补集合经验模态分解(complementary ensemble empirical mode decomposition，CEEMD)-BP神经网络模型，并通过汾河月径流预测实例对模型进行了验证，证明了该组合模型预测效果较好；徐冬梅等[8]基于完整集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)和小波分解(wavelet decomposition，WD)组合的二次分解方法，提出CEEMDAN-WD-PSO-LSSVM组合模型对洛河流域长水水文站月径流进行了预测，结果表明该组合模型具有较高的预报精度；王丽丽等[9]建立了奇异谱分析(singular spectrum analysis，SSA)-灰狼优化算法-支持向量机回归(support vector regression，SVR)模型，通过黑河正义峡月径流预测实例对模型进行了验证，结果表明该模型能够更深入地捕获水文径流的内在特性，具有更好的预测效果；孙望良等[10]引入变分模态分解(VMD)、去趋势波动分析(detrended fluctuation analysis，DFA)和长短时记忆神经网络(LSTM)方法，提出DFA-VMD-LSTM日径流预报模型对三峡水库日径流进行了预报，取得较好预报效果；黄景光等[11]基于小波分解方法和支持向量机(SVM)建立了组合日径流预报模型对宜昌站日径流进行预报，验证了该模型具有更好的预报稳定性；黄巧玲等[12]将小波变换与支持向量机相结合，提出利用小波支持向量机回归模型对泾河流域张家山水文站日径流进行预报，结果显示该模型可有效模拟和预报日径流；任化准等[13]融合小波分析方法、粒子群优化算法和支持向量机，构建了小波-粒子群-支持向量回归耦合日径流预报模型并对金沙江中游石鼓水文站日径流进行了预报，结果表明该模型在日径流预报中具有较强的适应性；张亚杰等[14]建立了经验模态分解(EMD)-法务侦查(forensic-based investigation，FBI)算法-极限学习机(extreme learning machine，ELM)组合径流预测模型，并将该模型应用于云南省姑老河水文站年径流的预测，获得了较好的预测效果。

然而，上述模型或方法存在以下问题或不足：(1)大多数径流预报仅针对预见期为1个月或1 d的单步预报，而在实际应用中，单步预报往往无法满足月径流或日径流预报的实际需求，须根据需要依据历史数据实现更多尺度的超前多步预报，即实现未来更为长远的径流时间点预报。(2)变分模态分解(VMD)和经验模态分解(EMD)等方法难以有效对原序列进行分解，如VMD的模态个数和惩罚因子难以确定，分解个数取值很大程度上影响了VMD的分解精度；EMD及其改进分解方法存在模态混叠、计算量大、复杂度高等问题。(3)预测模型中，Elman神经网络存在调节参数多、易陷入局部最优等缺点；SVR在处理大规模数据时预测精度不理想；LSTM网络预测性能较好，但存在计算量大、耗时长等不足。

为提高月径流或日径流时间序列多步预报精度，解决上述单步预测、分解方法和预测模型存在的问题，本文引入小波包变换(wavelet packet transform，WPT)、猎人猎物优化(hunter-prey optimization，HPO)算法和极限学习机(ELM)，建立WPT-HPO-ELM组合径流时间序列多步预报模型，并通过云南省南康河水文站月径流和日径流时间序列多步预报实例对模型进行了检验。

2 数据来源与研究方法

2.1 研究区概况与数据来源

南康河水文站位于云南省普洱市西盟县勐梭镇南康桥村，建于1981年，系怒江流域南康河干流控制站，控制径流面积902 km2，为云南省重要水文站和报汛站。南康河属云南省山区性水文站，河谷深切，洪水过程陡涨陡落，径流起伏变化十分剧烈。本文分别以南康河水文站1981年1月-2020年12月共480个月的月径流和2018年1月1月-2020年12月31日共1 096 d的日径流为研究对象，月径流和日径流时序变化曲线见图1。由图1可以看出，南康河水文站最大月径流为161.0 m3/s，最小月径流为4.1 m3/s，比值为39.3；最大日径流为241.0 m3/s，最小日径流为4.3 m3/s，比值为55.7。可见南康河水文站月径流和日径流在时序上呈现出典型的多尺度、高度非线性特征，波动变化剧烈。

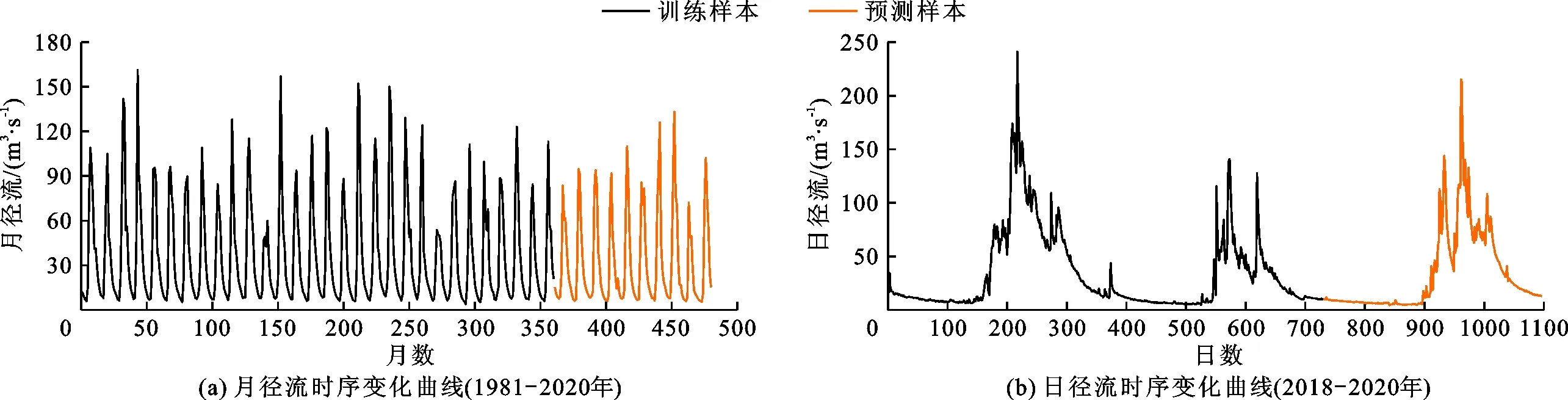
图1 南康河水文站逐月/逐日径流变化曲线

2.2 研究方法

2.2.1 小波包变换(WPT) 小波包变换(WPT)是一种特殊的小波变换(WT)，相对于WT只解析信号低频部分，WPT还能对信号高频部分进行进一步分解，更适用于径流时间序列分解，已在水文时间序列预测研究中得到应用[15-16]。

利用WPT对径流原始信号进行分解的公式[17-19]为：

(1)

重构算法为：

(2)

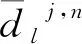
小波包变换的关键是小波基函数的选择，本文选择具有较好变换效果的demy小波基函数。

2.2.2 猎人猎物优化(HPO)算法 猎人猎物优化(HPO)算法是Naruei等[20]于2021年提出的一种新型群体智能优化算法。该算法灵感来自于狮子、豹子、狼等“猎人”攻击远离群体的雄鹿、瞪羚等猎物的行为，“猎人”向远处的猎物调整自己的位置以获得最佳狩猎位置，而猎物则向安全的地方调整自己的位置以逃避攻击，猎物最安全位置即为待优化问题的最优解。HPO算法设置参数少，寻优性能强，目前已在函数及工程优化中得到应用。

HPO算法数学原理简述如下[20]：

(1)初始化。HPO算法利用公式(3)在搜索空间中随机生成初始种群个体位置，描述如下：

xi=rand(1,d)·(ub-lb)+lb

(3)

式中：xi为猎人或猎物位置；ub、lb为搜索空间上、下限值；d为问题维度。

(2)猎人搜索策略。猎物通常成群结队，猎人常选择远离群体的猎物作为狩猎目标。该策略类似于算法中的探索策略，倾向于高度随机行为。猎人位置更新数学描述为：

xi,j(t+1)=xi,j(t)+0.5[(2CZPpos(j)-xi,j(t))+

(2(1-C)Zμ-xi,j(t))]

(4)

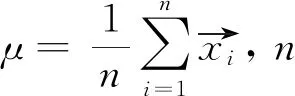
(3)猎物逃避策略。HPO算法中，猎物最安全位置即为全局最佳位置，因为只有这样才能使猎物获得生存机会。猎物位置更新数学描述为：

xi,j(t+1)=Tpos(j)+CZcos(2πR1)·(Tpos(j)-xi,j(t))

(5)

式中：Tpos为全局最优位置；R1为[-1, 1] 范围内的随机数； 其他参数意义同上。

为验证HPO算法的寻优能力，选取Sphere等6个典型测试函数在不同维度条件下进行仿真验证，其寻优结果见表1。基于MATLAB 2018a M语言实现HPO对6个典型测试函数的20次寻优，利用20次寻优平均值对HPO寻优性能进行评估。设置猎人或猎物种群规模N=50，最大迭代次数T=100，其他采用算法默认值。

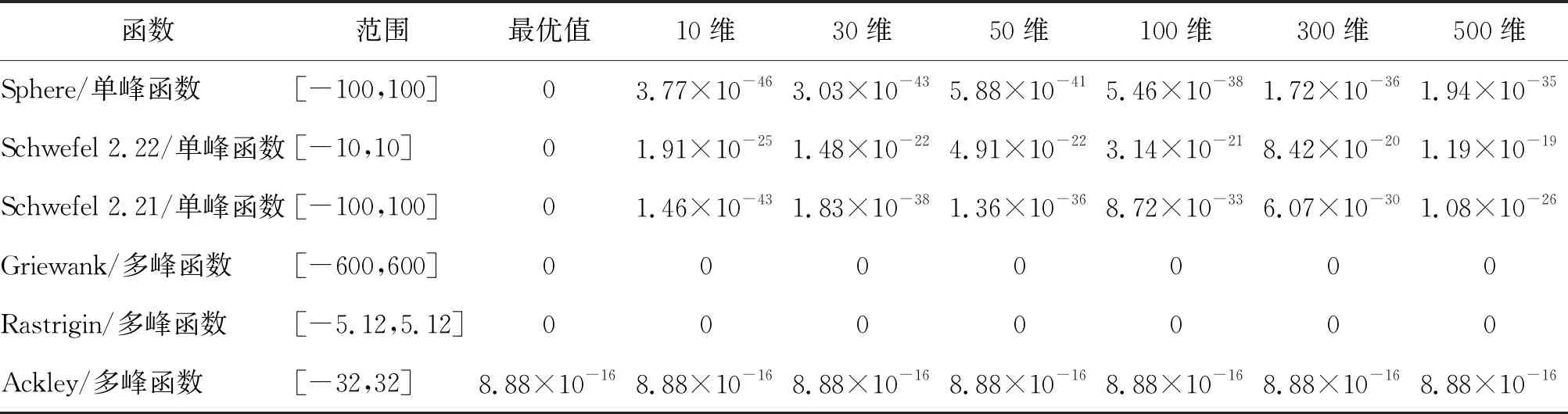
表1 HPO算法标准测试函数在不同维度条件下的寻优结果

由表1可知，对于单峰函数，HPO算法在不同维度条件下的寻优精度均在1.19×10-19以上；对于多峰函数，HPO算法在不同维度条件下寻优均获得了理论最优值，表明具有较好的寻优精度和全局搜索能力。

2.2.3 极限学习机(ELM) ELM是近年兴起的一种单隐层前馈神经网络(single-hidden layer feedforward networks，SLFNs)学习算法，具有学习速度快、泛化性能好等优点。在实际应用中，由于ELM随机给定的输入层权值和隐含层偏值易导致模型预测效果不佳，目前用于ELM关键参数优化的群体智能算法有爬行动物搜索算法[19]、灰狼优化算法[21]、鲸鱼优化算法[22]、黑猩猩优化算法[23]等。

给定M个样本Xk={xk,yk}，k=1,2,…,M，其中xk为输入数据，yk为真实值，设定f(·)为激活函数，隐含层节点为m个，则ELM输出可表示为[14]：

(6)

式中：oj为输出值；Wi={wi1，wi2，…，wim}′为第i个输入层节点与隐含层节点的连接权值；bi为第i个输入层节点和隐含层节点的偏值；λi为第i个隐含层节点与输出层节点的连接权值。

2.2.4 模型建立的流程

步骤1：为兼顾模型预报精度和计算规模，本文基于demy小波基函数，采用2层WPT对南康河水文站1981年1月-2020年12月月径流、2018年1月1日-2020年12月31日日径流时序数据进行2层小波包分解，即将各径流时序数据分解为4个子序列分量[2,1]、[2，2]、[2，3]、[2,4]，见图2。由图2可以看出，不同的子序列分量反映了径流的不同变化特征。直观上，[2,4]分量的频率最低，周期性明显，反映出径流数据的整体变化趋势；[2,3]分量波动性较为平缓，且频率相对较低，具有一定的周期性，反映出径流数据的周期性规律；[2,2]和[2,1]分量波动激烈且频率较大，周期性不明显，反映出径流数据的随机性。

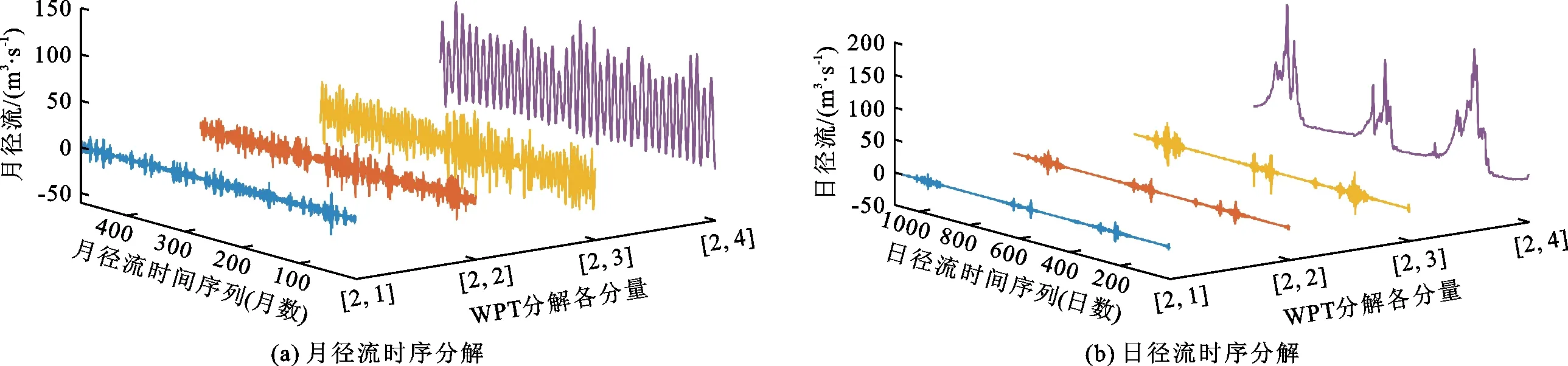
图2 南康河水文站径流WPT分解3D效果图

步骤2：为便于各分量预测结果重构，在延迟时间为1的条件下，采用Cao方法确定各子序列分量[2,1]～[2,4]的嵌入维数k，并利用前k月(日)的径流分量来预测当月(日)(即1个月或1 d)、第2月(日)(即2个月或2 d)、第3月(日)(即3个月或3 d)……的径流分量。预测模型的输入、输出表示为：

(7)

式中：Xinput和Youtput分别为月(日)径流预测输入值和输出值，m3/s；c为超前步数；u为月(日)径流序列长度；k为嵌入维数或滞后数。

利用Cao方法确定月径流子序列分量[2,1]～[2,4]的k值分别为13、16、24、20；确定日径流子序列分量[2,1]～[2,4]的k值分别为13、12、24、15。选取2011年1月-2020年12月月径流(120个月)、2020年1月1日-2020年12月31日日径流(366 d)作为预测样本，其余样本作为训练样本(参见图1)。

步骤3：利用训练样本均方误差(mean square error,MSE)构建HPO优化ELM输入层权值和隐含层偏值的适应度函数。

(8)

式中：Q′i为第i个径流实测值；Qi为第i个径流预报值；l为训练样本数； 其他参数意义同上。

步骤4：设置HPO算法最大迭代次数T=100，种群规模N=50，其他采用算法默认值；ELM网络激活函数选择sigmoid，隐含层节点数为2k(k为嵌入维数)，输入层权值和隐含层偏值搜索空间设置为[-1,1]，径流时序数据采用[-1,1]进行归一化处理。

步骤5：基于公式(3)在搜索空间随机初始化猎人或猎物个体位置xi；计算猎人或猎物个体适应度值，确定并保存最佳猎物位置Tpos。令t=1。

步骤6：在[0,1]范围内生成随机数R2，若R2<0.2，则基于公式(4)执行猎人搜索策略，更新猎人位置；否则基于公式(5)执行猎物逃避策略，更新猎物位置。

步骤7：基于猎人或猎物新位置计算适应度值，比较并保存当前最佳猎物位置Tpos。

步骤8：令t=t+1，判断是否满足终止条件，若不满足则转至步骤6。

步骤9：输出最佳猎物位置Tpos，Tpos即为ELM输入层权值和隐含层偏值最佳矩阵。利用最优ELM输入层权值和隐含层偏值矩阵建立HPO-ELM模型进行预测。

步骤10：利用平均绝对百分比误差(mean absolute percentage error，MAPE)、平均绝对误差(mean absolute error，MAE)、确定性系数(Cd)和合格率(Pr)对预报模型进行评估，该4个参数的计算方法见公式(9)～(12)。

(9)

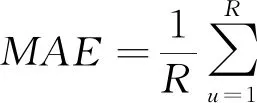
(10)

(11)

(12)

式中：Q′u为第u个径流实测值，m3/s；Qu为第u个径流预报值，m3/s；R为径流预报样本长度；Q″u为实测径流的平均值，m3/s；p为绝对百分比误差≤20%的样本数量。

步骤11：当月径流或日径流预报值的平均绝对百分比误差MAPE>30%时，停止WPT-HPO-ELM模型多步预报。

3 结果与分析

利用所构建的WPT-HPO-ELM模型对南康河水文站月径流和日径流进行训练及多步预报，不同预报月数、日数的月径流、日径流多步预报结果误差对比分别见图3、4，不同预报期的预报相对误差效果见图5。

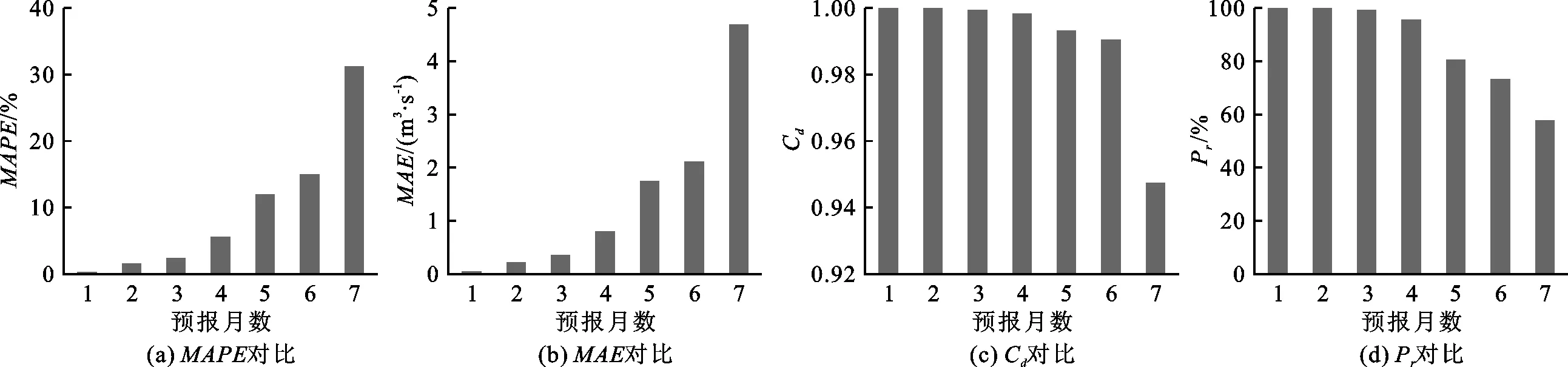
图3 不同预报月数月径流多步预报结果误差对比

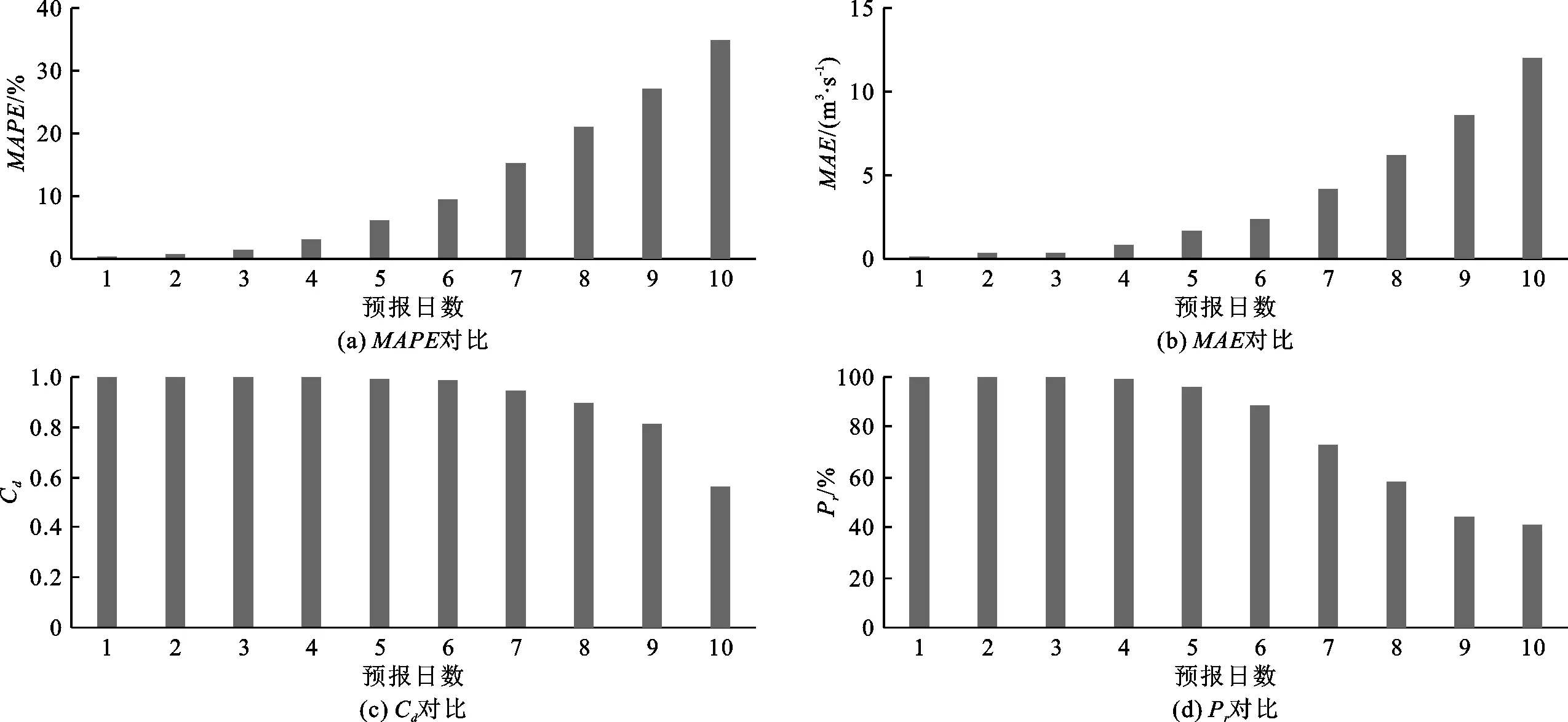
图4 不同预报日数日径流多步预报结果误差对比

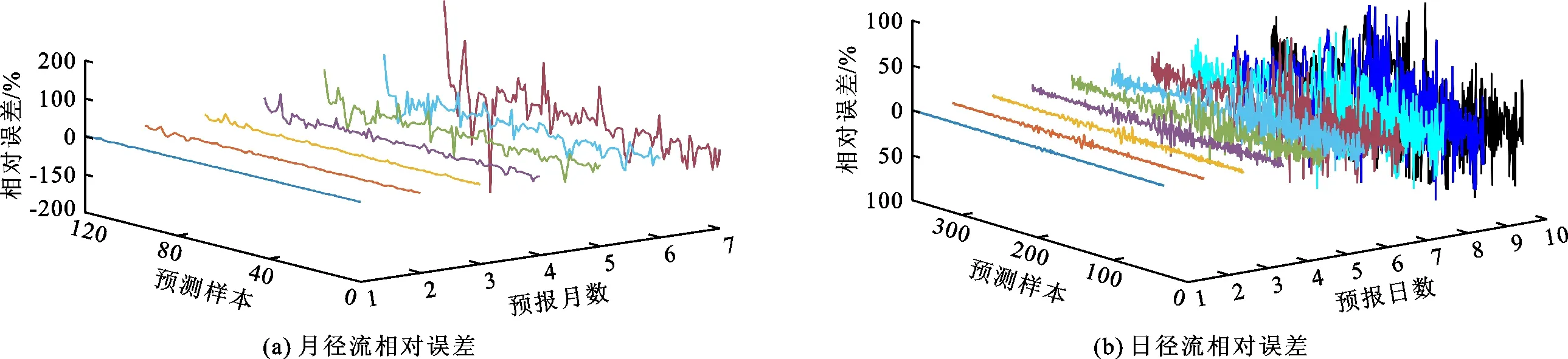
图5 不同预报期的月径流和日径流多步预报相对误差效果

分析图3～5可以得出：

(1)WPT-HPO-ELM模型对预报期为1～3个月的月径流具有理想的预报效果，预报结果的MAPE、MAE、Cd、Pr分别在0.33%～2.43%、0.047～0.352 m3/s、1.000 0～0.999 7、100%～99.2%之间；对预报期为4～6个月的月径流具有较好的预报效果，预报结果的MAPE、MAE、Cd、Pr分别在5.55%～15.0%、0.796～2.107 m3/s、0.998 6～0.990 7、95.8%～73.3%之间；当预报期为7个月时，预报结果的MAPE、MAE、Cd、Pr分别为31.2%、4.688 m3/s、0.9475、57.5%，预报效果较差，已不能满足月径流预报精度要求。

(2)WPT-HPO-ELM模型对预报期为1～3 d的日径流具有理想的预报效果，预报结果的MAPE、MAE、Cd分别为0.20%～1.23%、0.070～0.377 m3/s、1.000 0～0.999 6之间，Pr均为100%；对预报期为4～7 d的日径流具有较好的预报效果，预报结果的MAPE、MAE、Cd、Pr分别在3.03%～15.30%、0.851～4.166 m3/s、0.997 9～0.947 0、99.5%～73.0%之间；当预见期为8～10 d时，预报的MAPE≥21.1%、MAE≥6.236 m3/s、Cd≤0.898 3、Pr≤58.2%，预报效果相对较差，已不能满足日径流预报精度要求。

(3)图3、4表明，WPT-HPO-ELM模型对月径流和日径流时间序列预报误差随着预报期的增加而增加。在月径流预报期为1～6 个月、日径流预报期为1～7 d范围内，WPT-HPO-ELM模型预报结果可靠性较强、精度较高，将其用于月径流或日径流时间序列多步预报是可行的。

(4)图5表明，WPT-HPO-ELM模型对南康河水文站预报期为1～3个月的月径流预报中，86.7%样本的相对误差在-5%～5%范围内波动；对预报期为1～3 d的日径流预报中，97.5%样本的相对误差在-5%～5%范围内波动，具有更小的预报误差和更高的预报精度。

4 讨 论

时间序列预测方法较多，根据预测模型的不同可以分为传统预测方法、智能预测方法和智能混合预测方法3类。传统预测方法主要利用数学统计方法研究历史数据走势规律并建立回归模型来拟合未来数据，从而达到预测的目的，但对于非平稳时间序列的预测精度较差；智能预测方法主要融合优化算法与机器学习机，建立组合模型达到预测的目的，但对于高度非线性、多尺度时间序列难以获得满意的预测效果；智能混合预测方法主要通过多种算法、方法和模型相互组合优化，充分利用各算法的优点，达到提高模型预测精度的目的，如本文建立的WPT-HPO-ELM模型，其在实例月径流和日径流时间序列预报中获得较好的预报效果，主要得益于WPT方法、HPO算法、ELM网络三者的有机融合，模型及方法可在类似水文预报研究中进一步发展与推广。今后可在以下方面作进一步探索：

(1)将WPT与其他变分模态分解、小波变换、奇异谱分析、经验模态分解、改进经验模态分解等方法的分解效果作对比验证。

(2)WPT应用的关键是小波基函数的选择，目前小波基函数有harr小波、coifN小波、dbN小波、demy小波、cgua小波、mexh小波、sym8小波等。本文选择demy小波基函数，而基于其他小波基函数的WPT分解效果有待验证。

(3)虽然HPO算法在标准函数与ELM输入层权值和隐含层偏值的优化中具有较好的应用效果，但与传统粒子群优化算法、遗传算法等的优化效果的对比有待验证。

(4)ELM输入层权值、隐含层偏值与隐含层神经元节点数对ELM模型性能影响较大，本文利用HPO算法优化ELM输入层权值和隐含层偏值，但ELM隐含层神经元节点数的选取对月径流和日径流时间序列预报精度的影响有待进一步研究。

5 结 论

径流时间序列多步预报是水文预报研究领域的热点和难点。为提高径流时间序列多步预报精度，基于WPT方法、HPO算法和ELM网络，建立WPT-HPO-ELM径流时间序列多步预报模型，通过云南省南康河水文站月径流和日径流时间序列多步预报实例对WPT-HPO-ELM模型进行检验，得到如下结论：

(1)在不同维数条件下，HPO算法对Sphere等6个标准函数均具有较好的寻优精度，尤其是针对高维问题优化，HPO算法表现出较好的寻优效果，将HPO用于ELM输入层权值和隐含层偏值优化是可行的。

(2)WPT-HPO-ELM模型对预见期为1～3个月的月径流和1～3 d的日径流具有理想的预报效果；对预见期为4～6个月的月径流和4～7 d的日径流具有较好的预报效果；当预见期为7个月或≥8 d时，预报效果较差，已不能满足月径流或日径流预报精度要求。

(3)在月径流预报期为1～6个月、日径流预报期为1～7 d范围内，WPT-HPO-ELM模型预报结果可靠性较强，实测月径流或日径流值相近，将WPT-HPO-ELM模型用于月径流或日径流时间序列多步预报是可行的，该模型及方法可为实现径流时间序列精准预报提供新的途径。

(4)WPT-HPO-ELM模型能充分发挥WPT方法、HPO算法和ELM网络的优势，表现出较好的多步预报精度和稳定性能，模型预报误差随着预见期的增加而增加。