基于双重密度和簇间近邻度的密度峰值聚类算法

李沛武，张永芳，黄逸翠，刘紫亮，居 翔

(南昌工程学院 信息工程学院，江西 南昌 330099)

数掘挖掘因具有数据过滤的高效性和获取信息的便捷性而备受关注，聚类算法是其经典的技术[1]。聚类算法无需先验知识，根据样本点间的相似性将数据集划分成对应的簇[2]。聚类算法大致包括5种：基于划分的聚类、基于层次的聚类、基于密度的聚类、基于网格的聚类和基于模型的聚类，每一种算法都有其对应的优点和缺点[3]。

Rodriguez[4]等在2014年提出密度峰值聚类算法(Density Peaks Clustering，DPC)，该算法不同于传统的密度聚类，具有参数少、能发现非球状簇、对噪声点不敏感的特点。但对密度分布不均衡数据集聚类时，DPC算法未考虑样本点空间分布，会导致聚类效果不佳，在分配过程中易产生连带错误。为解决以上缺陷，很多研究者对DPC算法进行改进。针对局部密度计算方式存在的不足，文献[5]引入最近邻和共享近邻的概念，定义两步分配准则，提出基于共享近邻的密度峰值聚类算法(Shared-nearest-neighbor-based clustering by fast search and find of density peaks，SNN-DPC)，提高了算法对于不同数据集聚类的准确性。文献[6]引入逆K近邻的思想改进局部密度公式，缓解了DPC算法对密度不均数据集聚类效果不佳的问题。文献[7]融合共享K近邻和共享逆K近邻改进样本点间的相似性，改善了DPC算法不能很好处理簇间密度分布不均的情况。文献[8]将自然和共享近邻算法结合重新定义局部密度的计算规则，使算法在性能等方面有明显的提升。文献[9]将密度比例思想引入密度峰值聚类中，通过计算两个邻域内密度平均值之比来重新定义样本的相对密度，提高了对于密度较小类簇中心的识别度。文献[10]引入改进凝聚度的思想，使用节点凝聚度替代样本点相对密度的计算，通过在真实数据集和人工数据集上的实验证明，改进算法能找到更高精度的聚类中心。针对样本分配存在的不足，文献[11]借鉴万有引力公式，重新定义样本点与簇间的相似性，将未分配样本点划分给相似性高的簇，提高了在复杂数据集中样本点分配的正确率。文献[12]提出了两步分配策略，对于核心点按照密度递减的顺序分配给最近的簇中心点，对于离群点根据邻近样本点所属簇信息进行划分。改进算法不仅能很好处理含有噪声点的数据集，而且能适应大规模数据集。文献[13]提出新的样本分配策略，首先将簇中心的K个近邻点分配给对应的类簇，其次将未分配点划分给相互近邻度最高样本点所在的类簇，解决了数据集密度不均聚类效果不佳的问题。虽然上述改进算法都提高了算法的准确度，但部分算法未重视样本空间结构的影响。文献[14]提出样本点进行类簇分配时，不仅要考虑与密度较大点之间的距离，还要考虑K近邻对样本点的影响，改进算法减少了对密度较大样本点正确分配的依赖性。文献[15]提出结合K近邻思想的统计学习分配策略，根据样本点K近邻中属于各类簇的样本个数决定所属类簇，改进算法提高了样本分配的准确。文献[16]提出微簇融合策略，根据簇间密度差和簇间距离进行微簇合并，改善了剩余样本点分配的容错性，提高样本分配的效率。文献[17]利用第一宇宙速度建立两步样本点分配策略，通过每一个未分配样本点与簇类中心点之间的第一宇宙速度比较，把未分配点划分为必然属于和可能属于该类簇，针对可能属于该簇的样本点进行再一次对比，此分配方法使剩余样本点的分配更加准确。文献[18]将K近邻算法与图标签传播结合改进密度峰值聚类算法，利用K近邻图传播动态地对剩余未分配样本点进行类簇划分，提高了聚类的准确性。

针对DPC算法存在的问题，本文提出了一种基于双重密度和簇间近邻度的密度峰值聚类算法(Density peak clustering based on dual density and inter cluster proximity，DI-DPC)。首先，DI-DPC算法根据样本密度受局部特征和全局特征的影响，在融合K近邻和截断距离的基础上提出双重密度计算准则，提高了聚类结果的准确率；其次，根据样本点的相对密度和相对距离选出候选中心点，并将未分配样本点分配给距离最近、密度更大的样本点所在的簇，生成候选微簇；最后，根据簇与簇之间的近邻度进行簇间合并，缓解样本点连锁式错误分配的问题。通过实验证明，改进的算法有效地改善了对密度分布不均衡数据集聚类效果不佳和对未分配点划分类簇易出现连带错误的情况。

1 DPC算法

DPC算法假设簇中心周围近邻点的密度相对较小，且簇中心与其它密度更大点距离相对较远。因此DPC算法定义了局部密度ρi和相对距离δi两个变量。

假设数据集DN×M=[x1，x2，…，xN]T，其中N为样本个数，M为样本维数。DPC算法在计算局部密度ρi时，有两种计算方法，如式(1)～(3)所示：

(1)

(2)

(3)

式中dc为截断距离，dij为样本点i与样本点j间的欧氏距离。式(1)称为截距核，适用于数据量较大的数据集；式(3)称为高斯核，适用于数据量较小的数据集。

相对距离δi指样本点到最近局部密度更大点的距离。对于密度最大点，其相对距离δi表示样本点间距离的最大值；反之，相对距离δi表示样本点i与密度比其大的样本点间的最短距离，如式(4)所示：

(4)

计算出以上两个参数之后，构造以ρ为横坐标，δ为纵坐标的决策图，选择局部密度ρ和相对距离δ相对较大的样本点作簇中心，最后将未分配样本点划分给比其密度大且最近的样本点所在的簇。

2 DI-DPC算法

2.1 融合截断距离和K近邻的双重密度

针对DPC密度计算存在的问题，本文提出融合截断距离和K近邻双重密度计算方法，过程如下：

由于DPC算法聚类结果对dc取值比较敏感，本文根据文献[17]定义的公式计算dc，如式(5)所示，以减少计算过程中参数的使用量。

(5)

定义1基于K近邻的局部密度。根据样本点与K个近邻点的距离定义基于K近邻的局部密度，如式(6)所示：

(6)

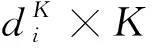
定义2基于截断距离的局部密度。在考虑样本点间结构的前提下，本文重新定义样本点i与其截断距离范围内样本点间的距离，如式(7)所示：

(7)

式中y_dc(i)为已划分类簇的集合；n_dc(i)为未划分类簇的集合。计算基于截断距离的局部密度步骤分三步进行：(1)将样本点i截断距离范围内的近邻点根据距离降序排列，同时将样本点i存入到y_dc(i)，将其它近邻点依照排序存入n_dc(i)；(2)依次计算y_dc(i)中样本点与n_dc(i)中样本点的最小距离，并将计算出最小距离的样本点由n_dc(i)移入中y_dc(i)并对计算出的距离求和；(3)直到n_dc(i)为空时，停止遍历。

定义3双重密度。融合K近邻和截断距离的双重密度计算公式，如式(8)～(9)所示：

ρave_i=(ρKnn_i+ρdc_i)/2，

(8)

(9)

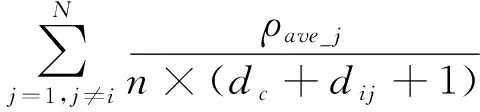
2.2 基于簇间近邻度的多簇合并准则

针对DPC算法分配策略存在的问题，本文提出基于簇间近邻度的多簇合并准则。进行多簇合并前需要生成候选簇，其过程为从依据式(4)～(9)计算出样本点相对距离和相对密度构造的决策图中获取p个候选簇中心点(C≤p≤5C，C表示实际类簇个数)，然后将未分配样本点依照密度降序划分给距离最近、密度更大的样本点所在的簇，显然生成的候选簇数量大于或等于实际的类簇数量。为获得更好的聚类结果，需要将相邻的或距离相近的簇进行合并，因此本文提出新的多簇合并算法规则定义如下：

定义4簇间近邻度。统计每个簇边缘点dc范围内其它簇的点个数，如式(10)所示：

(10)

(11)

式中截断距离dc根据式(5)定义；M(dij-dc)=1表示i点与j点不在同一个簇中且两者间距离小于截断距离，否则M(dij-dc)=0。mij表示样本点i所在簇与样本点j所在簇之间的近邻度，簇间近邻度越大，表明簇间相似性越大。

基于簇间近邻度的多簇合并过程主要计算候选簇间的近邻度mij，将计算出的mij放入构建的簇间近邻度矩阵，从矩阵中选择最大近邻度对应的两个候选簇进行合并，直到候选簇数等于实际簇数为止。

2.3 算法步骤及分析

综上所述，改进算法采用双重密度法则计算样本相对密度，依据DPC算法中类簇中心的选择机制选出候选类簇中心，将剩余样本点分配给邻近候选类簇，最后依据改进的类簇合并法则进行剩余样本点分配，从而形成最终的类簇。DI-DPC算法的具体流程如下：

step1 读取数据，对数据进行最大最小归一化处理；

step2 按照式(6)～(9)计算局部密度；

step3 根据式(4)计算相对距离；

step4 构建决策图，选出候选簇中心点；

step5 将未分配点划分给最近的密度较大点对应的簇；

step6 根据式(10)～(11)计算候选簇间的相似性，构建簇间近邻度矩阵；

step7 遍历簇间近邻度矩阵获得最大值，合并对应的候选簇；

step8 直到候选簇的个数等于真实簇个数时，输出聚类结果。

2.4 算法时间复杂度分析

为更好地分析DI-DPC算法的时间复杂度，本文先对DPC算法的时间复杂度进行分析。样本数为n的数据集进行密度峰值聚类的时间复杂度主要包括以下三个方面：(1)计算样本点相对密度时，需要两重循环遍历所有样本构建样本间的距离矩阵，因此其时间复杂度量级为O(n2)。(2)计算样本点相对距离时，需要对所有样本与其它样本的距离和密度进行比较，因此需要两重循环所有样本，其相应的时间复杂度量级为O(n2)。(3)在进行剩余样本点的分配时，根据剩余样本点与已选出的C(C表示实际类簇个数)个聚类中心点间距离进行比较，因此该阶段的时间复杂度为O(n×C)。综上所述，DPC算法的时间复杂度量级为O(n2)。

DI-DPC算法相较于DPC算法改进部分的时间复杂度主要包括：(1)改进的相对密度计算的时间复杂度包含以下两个步骤：基于K近邻的密度计算的时间复杂度为O(n×K)，其中K的取值远小于n的取值；基于截断距离的局部密度也需要双重遍历所有样本构建距离矩阵，其时间复杂度量级为O(n2)。因此该阶段整体的时间复杂度量级为O(n2)。(2)进行候选簇合并时，遍寻簇间近邻度表的时间复杂度为O(p×n)，其中C≤p≤5C。综上所述，DI-DPC算法的时间复杂度与DPC算法的时间复杂度量级一致为O(n2)。

3 实验结果与分析

本文使用9种经典人工数据集以及9种UCI真实数据集证明DI-DPC算法的有效性，并将DI-DPC算法与DPC[4]、SNN-DPC[5]、FCM[20]、K-means[21]、DBSCAN[22]进行性能对比，采用准确率(ACC)[23]、调整兰德系数(AMI)[24]、调整互信息(ARI)[24]作评价标准。采用Spyder进行实验，所有程序均采用Python实现。

在实验之前，对所有的数据集进行最大最小归一化处理如式(12)所示，使数据的不同特征归一到一个范围下，降低算法运算时间开销。

(12)

式中max(xj)、min(xj)分别代表j列中的最大值和最小值。

3.1 算法参数设置

为更好客观地测试各算法的聚类性能，本文对每种算法进行了参数调优。DI-DPC算法、SNN-DPC算法需要设置样本近邻数K，一般从1～20中选出最优参数作为样本近邻数K。K-means算法需要给出类簇数K，但K-means选取类簇中心点存在随机性，所以需要进行50次实验取最好结果。FCM算法需要事先指定类簇的个数K。DPC需要确定截断距离dc，取值参照文献[4]规定，使落入圆中点个数占数据集总数的1%～2%。DBSCAN需要确定邻域半径ε和最小样本点数Minpts，邻域半径ε取值从0.01～1.20，步长为0.01；最小样本点数Minpts取值从1～50，步长为1。

3.2 人工数据集结果分析

采用人工数据集实验的主要目的是比较每种算法在不同数据集上的聚类效能。表1列出了9种人工数据集的具体属性信息以及DI-DPC算法在9种人工数据集上的聚类结果。

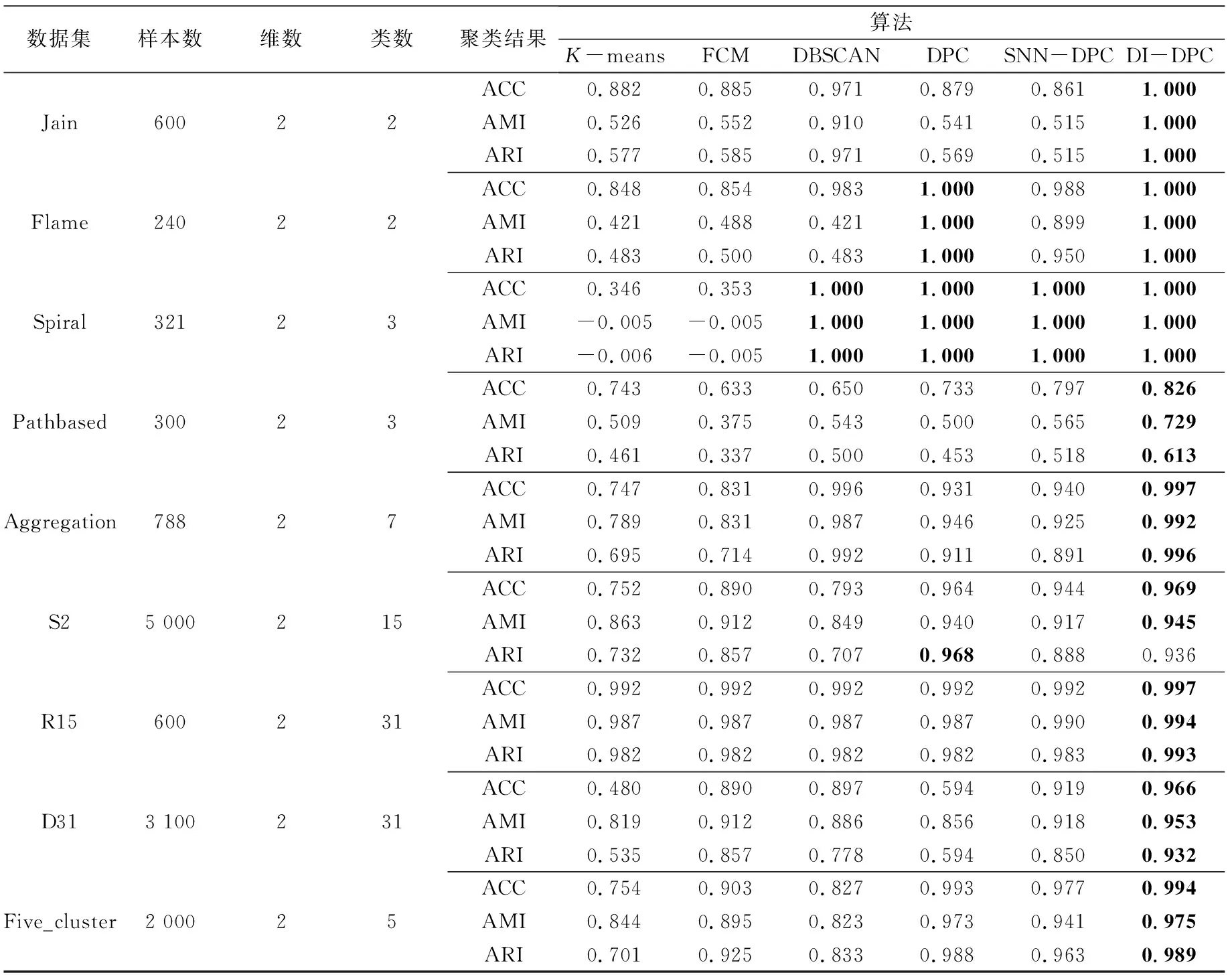
表1 人工数据集及其聚类结果

表1是6种算法在人工数据集上的对比结果，加粗加黑的部分表示结果中相对较好的。具体情况是：在Jain数据上，DI-DPC算法的性能最好，评价标准的取值都可达到最大值1.000，而SNN-DPC、K-means及FCM的性能相对较差；在Aggregation和Flame数据集，DPC和DI-DPC算法相较于K-means和FCM聚类结果是较优；在Spiral数据集上，K-means、FCM聚类效果较差，其余4种皆可取得最优值；在R15数据集上，4种经典算法及SNN-DPC算法的准确率仅有0.992，而DI-DPC算法的准确率为0.996，准确率提高了0.4%；在Pathbased、D31、S2、Five_clusters数据集上，DI-DPC算法为6种算法中的最优算法，ACC、AMI和ARI都有较大的提高。为更好证明DI-DPC算法的优越性，本研究选取3种聚类算法在3组人工数据集上的聚类效果图进行详细说明，其中效果图中不同形状的样本点代表不同的类簇。

Jain数据集中两个簇的密度相差较大，上半部分密度较为稀疏，下半部分密度较大。簇间密度不均导致聚类中心点选取易在一个簇中。通过图1可以看出，3种算法中只有DI-DPC算法分类是正确的；DPC、SNN-DPC都错误地将一个簇划分成两个。相比之下，在处理Jain数据集时，DI-DPC算法更好。

图1 3种算法对Jain数据集的处理结果

Five_clusters数据集中样本点总体密度较大且数据集相对较为密集。从图2可知，3种算法对于Five_clusters数据集处理的结果中，SNN-DPC算法和DI-DPC算法对于该数据集的分类是相对较好的，但DI-DPC算法对两簇间的样本点的聚类效果更好，DI-DPC算法的聚类效果更优。DPC算法存在将一个簇划分为2个簇的情况，聚类结果相对较差。

图2 3种算法对Five_clusters数据集的处理结果

Aggregation数据集是由7个相对集中的类簇组成，其中部分类簇之间相互连接。由图3可以看出，DPC、SNN-DPC算法错误地将一个完整的类簇划分为两个类簇；DI-DPC算法较好地保留了类簇的完整性。整体上来看，在Aggregation数据集上，DI-DPC算法的性能较好。

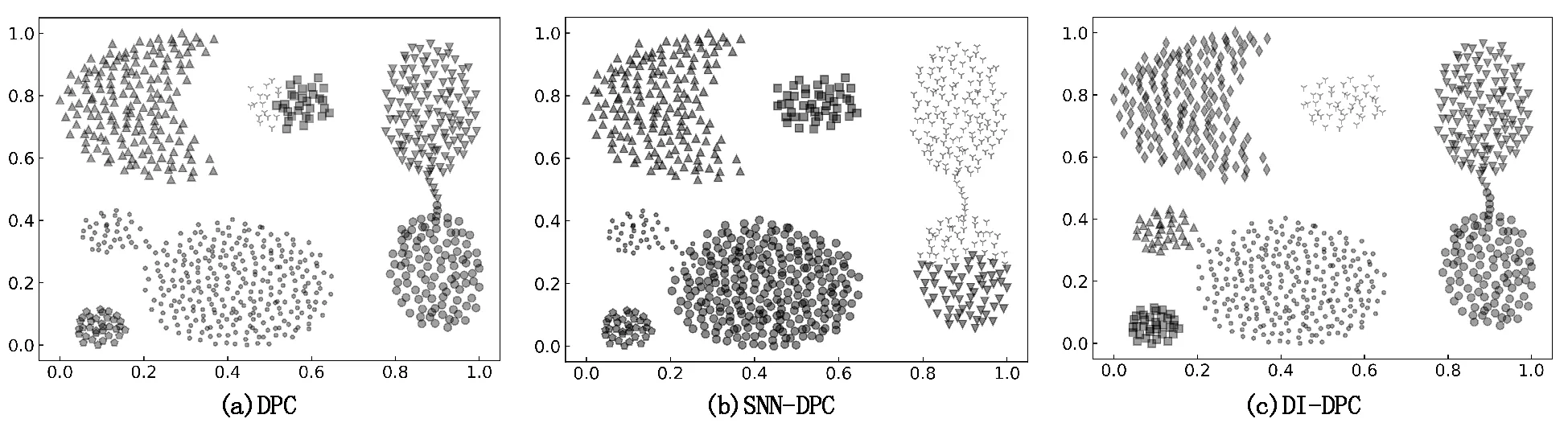
图3 3种算法在Aggregation数据集上的处理结果

综合上述内容，可以看出DI-DPC算法在处理人工合成数据集的时候，可以获得良好的聚类结果。

3.3 UCI数据集结果分析

为了进一步验证算法的效果与性能，本文选择了9种规模和维度有较大区别的UCI数据集。表2中总结了9种UCI数据集的相关属性，以及DI-DPC算法与K-means、DPC、DBSCAN、SNN-DPC算法在ACC、AMI、ARI上的对比。

通过表2可看出，DI-DPC算法相对于其它4种算法有不同程度的提高。在Wine数据集上，DI-DPC算法的AMI和ARI取值次于SNN-DPC算法，但ACC值高于4种对比算法；在Movement_libras数据集上，本文算法的ACC值低于SNN-DPC算法，但其它两个评价函数的取值高于其它算法；在其它数据集上，DI-DPC算法的聚类效果好于其它4种对比算法。通过上述分析可以得到，DI-DPC算法聚类效果更好。

表2 UCI数据集

4 结束语

针对DPC算法存在的问题，本文提出了基于双重密度和簇间近邻度的密度峰值聚类算法。DI-DPC算法提出了基于K近邻和基于截断距离的双重密度计算公式，提高了对密度不均衡数据集聚类时的准确性，同时增强了不同空间结构样本的相互作用；提出了新的簇合并法则，改善了DPC算法分配策略的不足之处。通过在人工合成数据集以及UCI真实数据集聚类结果证明，DI-DPC算法相较于经典聚类算法、SNN-DPC算法都取得良好的分配结果。但DI-DPC算法在选取聚类中心时，会受到人为选择和经验值的影响，造成额外的时间成本，因此自动获取聚类中心将会是下一步实验的方向。