一种可用于高阶调制格式的自动偏压控制技术

黄嘉琦，金 鑫，吴金洋，王元祥，杨 奇，戴潇潇

(华中科技大学 a.光学与电子信息学院； b.网络空间安全学院，武汉 430074)

0 引 言

为了提升系统的频谱效率，以应对高速大容量的传输需求，人们对高阶调制技术进行了研究，且已成功实现了4 096进制正交振幅调制(4 096-ary Quadrature Amplitude Modulation, 4 096QAM)的传输[1]。高阶调制信号的星座点密集，噪声容限低，易产生误码，需要先保证调制器输出的信号质量以降低最终的误码率。

同相正交(In-phase Quadrature，IQ)调制器由两个马赫曾德尔调制器(Mach-Zehnder Modulator，MZM)和一个相位调制器构成，其偏压易受到温度和压力等环境因素影响而发生偏移，导致信号质量劣化。因此需要控制调制器工作在最佳偏置点，现有的控制方案主要有基于导频和非导频两类。2006年，Cho P S团队提出了基于非导频的功率监测方案，通过监测功率极值来控制偏压[2-3]；2010年， Kawakami H等人则向IQ调制器两路加载正交导频信号，使用锁相放大器来监测偏压[4-5]；2017年，Li等人提出了一种基于导频的相关检测方案，通过计算相关系数值来监测偏压,以提高系统灵敏度[6]；2019年，Zhu等人则提出可通过监测谐波比值的方式来实现偏置点控制[7]。

本文提出一种新型的基于导频的自动偏压控制方案，结合了相关检测与相干探测技术，可提高系统的灵敏度和控制精度。向IQ调制器两路加载正交导频信号，将本振光中心频率偏移后与已调信号光用探测器接收，将功率电信号与正余弦信号进行相关运算，通过监测相关系数来控制偏压。本文对此方案的原理进行了仿真验证，结果与理论吻合。

1 原 理

常见的铌酸锂IQ调制器由两个MZM和一个相位调制器组成，改变加载在调制器上的偏置电压，调制后信号的幅度/相位也会改变。为了保证IQ调制器输出的信号质量，需要分别控制3个调制器的偏置电压，使得IQ调制器两路的MZMI和MZMQ能够工作在零偏置点，以减小调制器非线性的影响，同时控制相位调制器引入90 °的相位差，使得I路和Q路信号正交。然而铌酸锂材料易受到温度和压力等环境因素的影响，当环境发生细微变化时，调制器的最佳偏置点则会发生偏移，因此需要了解最佳偏置点对应的特性，以便能够监测到偏置点的漂移，并及时调整偏置电压使得调制器能稳定工作在最佳偏置点。

本文提出的基于导频的自动偏压控制方案结合了相干探测和相关检测技术。在偏压控制系统中使用相干探测技术，有利于微弱信号的探测，以提高系统的灵敏度；而相关检测技术则可以凸显出频点随偏压变化的规律，可进一步提高系统的灵敏度和控制精度。自动偏压控制系统框图如图1所示，分别在MZMI和MZMQ的偏置端口加载一个低频的导频信号，两个导频信号正交，其中VditherI=Acos(2πfct)为向I路MZM加载的导频信号，VditherQ=Asin(2πfct)为向Q路MZM加载的导频信号，fc为导频频率，A为导频幅度，t为时间。为了减小通信系统中导频引入的额外通信代价，导频信号幅度不宜过大。将激光分成两束：一束通过IQ调制器得到调制后的光信号；另一束则通过声光调制器(Acousto-Optic Modulator，AOM)得到中心频率偏移了f(f为经过AOM移频的频率)后的本振光信号，分出一束调制后的信号光ES与本振光信号ELo耦合后用光电探测器(Photoelectric Detector，PD)接收，通过模/数转换器(Analog to Digital Converter，ADC)采集得到的电信号功率P(t)，用于对偏置电压进行监测控制。可通过数/模转换器(Digital to Analog Convertor，DAC)将调好的电压信号加载到调制器的直流偏置端口。

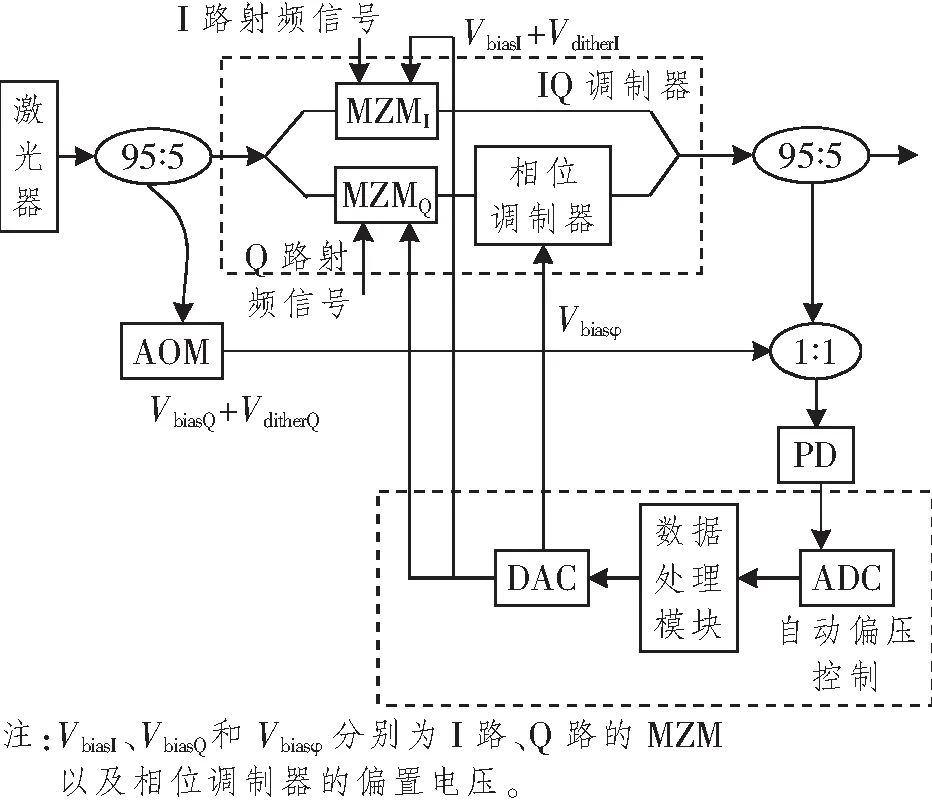
图1 自动偏压控制系统框图Figure 1 Diagram of automatic bias control system

电信号功率P(t)的表达式如下：

式中：VI和VQ分别为向I和Q路MZM加载的总信号；Vπ为半波电压；φ为I路和Q路信号之间的相位差；VbiasI/Q中的VbiasI和VbiasQ分别为I路和Q路MZM的偏置电压；j为虚数单位；VdI/Q中的VdI和VdQ则分别为I路和Q路MZM偏置电压的偏移量，VdI/Q=0时表示I路或者Q路的MZM正处于最佳偏置零点，此时载波正好被充分抑制。当φ=90 °时，频点f+fc的功率最低。因此，考虑将P(t)分别与cos(2πft)、sin(2πft)和sin[2π(f+fc)t]进行相关，并根据贝塞尔展开公式的Jacobi-Anger等式对公式进行处理，如式(3)所示：

式中：C1、C2和C3均为相关系数；T为积分时间；J0和J1分别为0阶和1阶贝塞尔函数。固定MZMI和MZMQ的偏置电压VbiasI和VbiasQ，可以看出当相位调制器工作在最佳偏置点，即φ=90 °时，C3=0。因此在监测相位调制器的偏置电压Vbiasφ时，需要计算相关系数C3，找到C3=0对应的电压值，作为φ=90 °时对应的偏置电压。

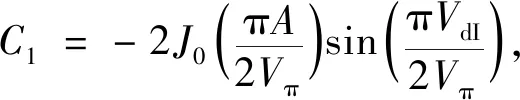
当Vbiasφ发生偏移时，φ不为90 °，如式(3)所示，C1会因为第2项中cosφ的影响，不能在MZMI的最佳偏置点取到零值，从而引入误差。当VbiasI和VbiasQ发生轻微偏移时，并不会影响C3取零值的结果，因此不会引入对Vbiasφ的监测误差。所以实际中对3个偏压进行监测控制时，需要先计算C3，将C3=0对应的电压值作为相位调制器的偏置电压并固定后，再分别计算C1和C2，找到零点对应的电压值，分别为MZMI和MZMQ所需要的最佳偏置电压。

2 仿真验证

图2 未加载射频信号时相关系数随偏置电压变化的曲线Figure 2 Curves of correlation coefficient varying with bias voltage when RF signal is not loaded

在Matlab软件上对本文所提偏压控制方案进行仿真，在该仿真系统中，设置AOM移频的频率f=55 MHz，导频信号的频率fc=10 kHz，幅度为10%Vπ。首先对未加载射频信号的情况进行仿真，得到的相关系数曲线如图2(a)～2(c)所示。在φ=90 °，而VbiasQ处于不同值的情况下，在0～2Vπ的范围内扫描VbiasI，计算得到C1和VbiasI的曲线图如图2(a)所示；同理，图2(b)所示为固定φ=90 °，VbiasI为不同值的情况下，在0～2Vπ的范围内对VbiasQ进行扫描，计算得到的C2与VbiasQ的曲线图。由图可知，当且仅当VbiasI或VbiasQ等于Vπ时，即在最佳偏置点零处，满足C1=C2=0；当VbiasI或VbiasQ等于0/2Vπ时，C1或C2则为曲线的极值，这均与式(3)中C1和C2的表达式相符合。图2(c)所示为在VbiasI和VbiasQ的多种取值情况下，扫描相位调制器的偏置电压计算得到的C3与φ的曲线图，φ的扫描范围为0～180 °。由图可知，当且仅当φ=90 °时，C3可取得零值，曲线趋势也与原理中的表达式完全相符，因此可初步验证本方案的可行性。

为验证本文所提偏压控制方案在加载了射频信号的系统中的可行性，在上述平台分别对10 GBaud 16QAM、64QAM以及256QAM的系统进行仿真，导频信号的幅度固定为A=10%Vπ，射频信号峰峰值为Vπ，此时对应的调制深度为70%，结果如图3(a)～3(c)所示。由图可知，在加载了射频信号的情况下，C1、C2和C3的零点依然对应3个偏置电压的最佳值，相关系数随3个偏置电压变化的曲线也与原理符合。因此在信号传输过程中，可以通过计算并找到几个相关系数零点的方式，进行偏置电压的实时监测控制。并且对于仿真涉及的3种不同调制格式，尤其是对于64QAM和256QAM这样的高阶调制信号，本文提出的新型自动偏压控制方案都是可行的。

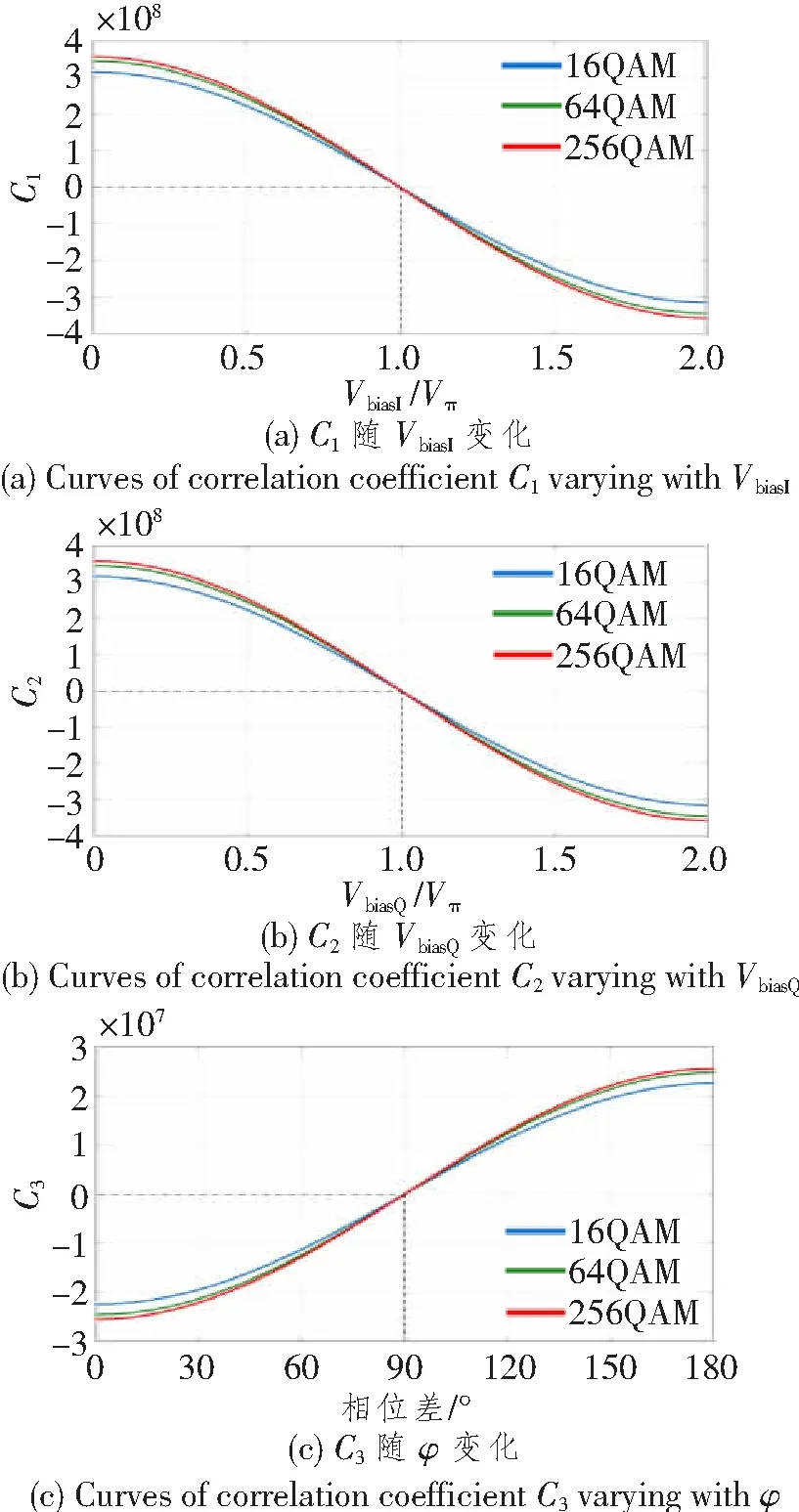
图3 不同调制格式下相关系数随偏置电压变化的曲线Figure 3 Curves of correlation coefficient varying with bias voltage for different modulation formats

对于10 GBaud 256QAM的系统，针对不同射频信号的峰峰值情况进行仿真。固定导频信号的幅度A=10%Vπ，对比了射频信号的调制深度分别为25%、50%、75%和100%的结果，如图4(a)～4(c)所示。可见在这几种不同的调制深度下，相关系数的零点均对应最佳偏置点，与原理符合。并且不同调制深度的相关系数曲线的单调性相同，因此系统中每个相关系数随偏置电压改变的方向是固定的，这更易于在对偏置电压进行扫描的过程中快速锁定最佳偏置点。

图4 不同调制深度下相关系数随偏置电压变化的曲线Figure 4 Curves of correlation coefficient varying with bias voltage at different modulation depths

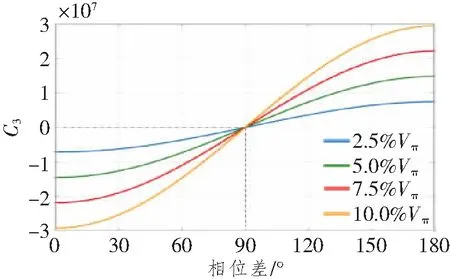
图5 不同导频幅度下C3随φ变化的曲线Figure 5 Curves of correlation coefficient C3 varying with φ for different pilot signal amplitudes

由于导频信号的幅度过大会影响接收端的信号质量，带来额外的误码，因此通常会选择低幅度导频。对不同导频信号幅度下的结果进行了仿真，由于对偏置电压VbiasI/Q的监测并不涉及导频信号，因此本文仅分析了导频的幅度对C3随φ变化的影响，仿真结果如图5所示。由图可知，在不同的导频信号幅度下，都能满足C3的零点对应相位差为90゜的位置，即相位调制器的最佳偏置点。但如图5中深蓝色曲线所示，当幅度A=2.5%Vπ时，与其他曲线相比，该曲线在最佳值附近的斜率有明显的降低。这是因为偏置电压发生较小程度的偏移时，进行相关运算会难以分辨出频点的细微变化，从而对偏压控制的精度有所影响。

为了验证本文方案的提升效果，本文在10 GBaud 256QAM的系统中，将此方案与基于快速傅里叶变换(Fast Fourier Transform，FFT)运算监测频点功率的方案[8]进行了仿真对比。分别对VbiasI、VbiasQ和Vbiasφ进行扫描，计算区分度，这里定义区分度为当前偏压下的功率或相关系数与扫描初始偏压下的值之间的差，结果如图6所示。仿真结果表明，与仅基于FFT的方案相比，对于MZMI和MZMQ，本文方案区分度分别提高了11.6和10.7 dB，而对于相位调制器，区分度则提高了11.7 dB。可见，与仅监测频点功率相比，使用相干探测和相关检测技术可有效提高系统的灵敏度，易于对偏置电压进行控制。

图6 256QAM系统中区分度随偏置电压变化的曲线Figure 6 Curves of distinguish ratio varying with bias voltage in 256QAM system

3 结束语

本文提出了一种新型的基于导频的自动偏压控制方案，结合了相干探测和相关检测技术。其中利用相干探测技术可有效刺激信号功率，提高系统的灵敏度；而相关检测技术则可凸显出频点随偏置电压变化的特性，从而降低噪声的影响，达到提高系统控制精度的效果。本文对此方案进行了理论分析，并通过仿真对方案的可行性进行了验证。仿真结果表明，本文方案可应用于16QAM、64QAM和256QAM等高阶调制系统，且在不同的信号调制深度和导频幅度的仿真场景下均成立。最后在256QAM系统中，将本文所提方案与基于FFT的方案进行了仿真对比，结果表明，对于MZMI、MZMQ和相位调制器，本文所提方案的区分度分别提升了11.6、10.7和11.7 dB，可见本文方案在系统灵敏度方面有明显提升效果。