基于高斯过程回归的光纤非线性信道补偿方法

吴 彪, 李嘉浩, 张召才

(1.国网电力科学研究院武汉南瑞有限责任公司，武汉 430074； 2. 武汉大学 电气与自动化学院，武汉 430072；3. 北京空间科技信息研究所，北京 100094)

0 引 言

非线性信道均衡是光纤传输系统中一个热门的研究方向，非线性效应从根本上限制了当前光纤通信系统的信息速率和传输距离[1]。目前，用于强度调制和直接检测 (Intensity Modulation Direct Detection，IMDD) 光纤链路的最流行的非线性信道均衡器(Channel Equalizer，CE)是最大似然序列均衡器 (Maximum Likelihood Sequence Equalization, MLSE)[2]和基于 Volterra 级数的非线性滤波器[3]。然而，这些非线性CE的计算复杂度很高，随着通道响应的维度呈指数增长。

最近，基于机器学习的非线性CE在提高 IMDD 光纤链路中的非线性容限方面显示出了巨大的潜力，例如神经网络 (Neural Network，NN)[4-5]、径向基函数网络 (Radial Basis Function Network，RBFN)[6]、支持向量机 (Support Vector Machine，SVM)[7]和长短期记忆递归神经网络 (Long Short Term Memory-Recurrent neural network，LSTM-RNN)[8]。与这些非线性CE相关的一个常见问题是这些机器学习模型中参数的物理意义尚不清楚。由于机器学习技术被用作“黑匣子”，因此模型中的参数是否已被调整为最优，或者参数如何影响系统性能尚不清楚。

本文使用基于高斯过程回归(Gaussian Processes for Regression，GPR)的非线性通道均衡。在线性损伤得到补偿的条件下，提出了用于非线性噪声抑制的GPR模型。在实验演示中，在100 km标准单模光纤(Standard Single Mode Fiber，SSMF)上传输 28-GBaud 4幅度脉冲幅度调制 (4-level Pulse Amplitude Modulation，PAM4)信号来构建IMDD链路。实验结果表明，基于GPR的非线性CE与传统的基于线性或非线性CE相比具有更好的性能。本文还比较了GPR和NN模型在非线性信道均衡方案中的性能，结果表明，GPR模型的输出可以看作是具有优化参数和无限宽度的NN模型输出的均值。

1 GPR的原理

多径通信系统中的非线性效应可以用函数g(·)建模为

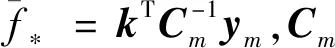
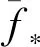
在无线通信系统中，以下协方差矩阵已被应用于GPR[10]中来实现非线性信道均衡：

式中：θ=[α1,α2,α3,γ1,γ2,…,γn]T为超参数，将在训练阶段确定；δij为Kronecker的delta函数。在式(5)中，第1项是平方指数协方差函数，它是无限可微的。由于平方指数协方差函数是xi-xj的函数，它持有监督学习中的关键假设：若输入数据xi和xj较接近，则可以认为他们会有类似的目标输出y。参数α1与目标y的方差有关。在平方指数协方差函数中，参数γl确定元素xi和xj之间的依赖程度。等式第2项表示线性回归，也称为点积协方差函数。等式第3项表示高斯白噪声的方差α3=σ2。

在实际场景中，超参数的值θ通常是未知的。为了解决这个问题，首先引入边际似然函数log[9]：

式中，Const.=(m/2)·log(2π)。由式(6)可知，超参数的最优设置θ对应于log函数的最大化。通过计算log函数θ的偏导数，一般采用了一种有效的计算方法，其中超参数可表示为[9]

2 GPR辅助的数字信号处理算法

图1 GPR辅助的非线性CE的数字信号处理流程Figure 1 DSP scheme of the proposed GPR-aided nonlinear CE

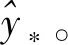
式中：Pch为测试数据集的信道功率；Pref为训练集的信道功率。因此，当输入功率值发生变化时，无需重新训练 GPR 模型。

3 实验结果

为了验证GPR辅助非线性CE在噪声估计模式和符号估计模式中的有效性，本文进行了IMDD的实验，并在100 km SSMF中传输了28-GBaud的PAM4 信号。实验装置如图2所示。信号帧由200个用于时间同步的开关键控(On-Off Key，OOK)符号和60 000个数据PAM4符号组成。数字信号是离线生成的，过采样因子为2，滚降因子为0.1。将数字信号加载到以56 GSa /s采样率运行的任意波形发生器中，以实现数/模转换。模拟信号的峰峰值电压最大为1 V。模拟电信号在1 550.8 nm、带宽为18 GHz的直接调制激光器中转换为光信号。直接调制激光器的线性度通过设置偏置电压来优化。为了克服光纤色散引起的功率衰落效应，采用光带通滤波器(Optical Bandpass Filter，OBPF)来产生光单边带信号。然后用掺铒光纤放大器(Erbium Doped Fiber Application Amplifier，EDFA)来补偿由OBPF引起的功率损耗，并将光信号输入到长度为100 km的SSMF中。经过光纤传输后，光信号由另一个 EDFA进行放大，然后由带宽为40 GHz 的光电探测器 (Photodetector，PD)转换为电信号。需要注意的是，EDFA可用于调整接收端PD的光功率。这主要是因为PD没有集成跨阻放大器，只能在输入功率>0 dBm的情况下正常工作。最后，模拟信号在数字采样示波器(Digital Storage Oscilloscope，DSO)中以80 GSa/s的采样率实现模/数转换。如图 1 所示，离线的数字信号处理过程包括重采样到过采样、时间同步、FFE、使用GPR 的非线性CE、解映射和判决以及BER计算。为了更好地评估基于GPR非线性CE的有效性，FFE的工作方式主要基于线性滤波器，滤波器抽头数设置为 67。为了公平比较，我们还在实验演示中考虑了基于NN模型的非线性CE，如图1所示[4]。

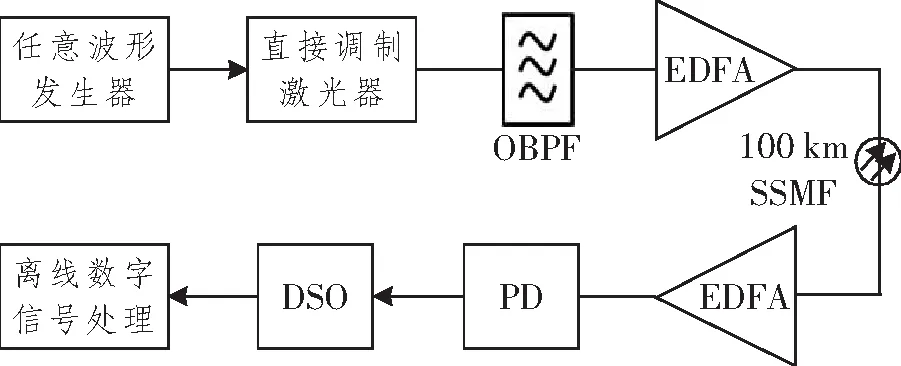
图2 56 Gbit/s 100 km IMDD实验装置图Figure 2 Experimental setup of the 56 Gbit/s IMDD fiber transmission link over 100 km

为了避免过拟合问题并确保训练/测试集的随机性，每个PAM4传输序列是通过将SIGN(·)函数应用于两个独立的二进制随机序列生成的，每个随机序列都来自一个AWGN序列。在实验演示中，使用长度为4 000的PAM4序列作为训练集。然后生成另外3个长度为60 000的不同PAM4序列作为测试集。BER是通过在测试过程之后对所有3个PAM4序列的BER进行平均来计算的。

通过在信道均衡阶段应用线性CE，当针对每个发射功率单独训练GPR 模型时，具有两种操作模式的GPR CE的性能如图3(a)所示。如图所示，经过线性CE之后，基于GPR模型的CE比没有使用GPR模型的CE的性能更好。两种GPR模式的性能相似。接下来，我们仅使用发射功率为16 dBm时获得的GPR模型来测试所有发射功率范围内的信号。如图3(b) 所示，噪声估计模式可以提供比符号估计模式更好的性能。当真实发射功率和参考发射功率之间的差异变大时，符号估计模式的性能会迅速下降。

图3 GPR辅助CE的BER性能Figure 3 BER performances of GPR-aided CEs versus launch power with GPR models trained at

然后，我们考虑线性均衡之后的NN非线性CE，将其性能与基于GPR的非线性CE进行比较。NN模型由具有维数 (9×1) 向量的输入层、具有200个节点的隐藏层和一个与估计噪声对应的输出节点构成。我们选择整流线性单位函数作为激活函数。如图4(a) 所示，使用GPR的非线性CE的性能优于使用NN的非线性CE，使用NN的非线性CE相比于线性CE也有一定程度的性能提升。

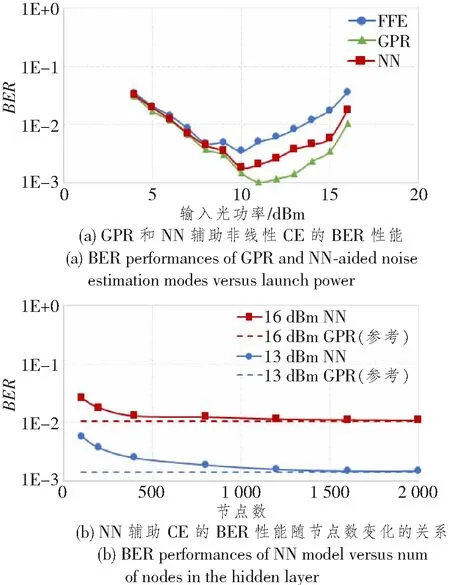
图4 GPR辅助CE的性能与参数的关系Figure 4 Relationship between GPR-aided CE performance and parameters

对于图4(a)中结果的解释是，若NN模型的宽度是无限的，则NN模型计算的函数是从多维中心极限定理意义上的高斯过程得出的函数。因此，当NN模型进行随机优化训练时，可以认为GPR在非线性建模中的表现优于NN。接下来，我们对隐藏层中节点数量的影响进行评估。具体来说，BER是通过对每个节点数量使用不同的随机初始化运行NN模型100次来平均的。如图4(b) 所示，随着节点数量的增加，NN模型的性能不断接近GPR模型。因此，GPR辅助非线性CE的输出可以看作是具有无限宽度和优化参数的NN辅助非线性CE输出的平均值。

我们还研究了训练数据的长度和维数n如何影响GPR在训练阶段的表现。如图5(a)所示，训练数据长度越大，性能越好。这主要是因为，如果在训练阶段应用更多的训练符号，多维高斯分布的逼近会更准确。由图 5(b) 可知，发射功率为13和16 dBm两种情况的最优维数n均为9。需要指出的是，式(5)中的协方差函数假设输入向量中的元素具有相同的长度尺度xl。在我们看来，维数n与符号之间的相关程度有关，可以根据光纤长度进行优化。

图5 GPR辅助CE的参数对BER性能的影响Figure 5 BER versus length of training symbols and number of dimensions n in GPR model

4 结束语

本文提出了GPR辅助的CE来减轻IMDD光纤链路中的非线性噪声。研究结果表明，GPR模型可用于在常规线性均衡后进一步提高系统性能。此外，本文还对GPR和NN模型在CE中的性能进行了比较，以证明GPR模型相对于NN模型的优越性。