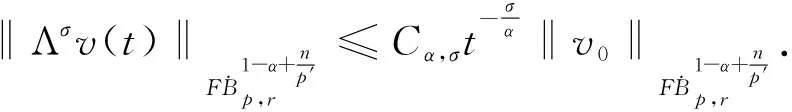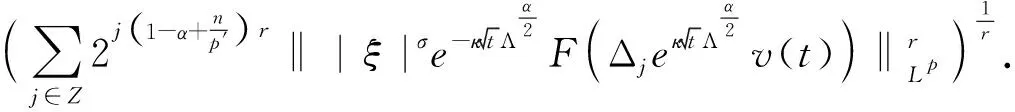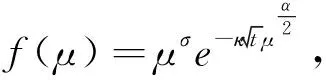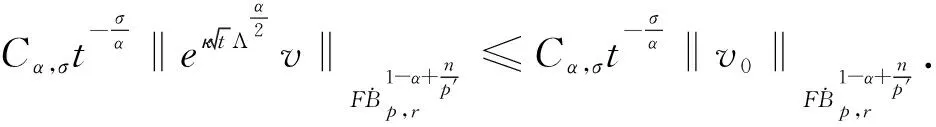不可压流在Fourier-Besov空间中的Gevrey正则性及时间衰减
张 瑜
(南京财经大学 应用数学学院, 江苏 南京 210023)
0 引言
长期以来,分数次扩散可压缩流体模型的研究获得广泛关注[1-7],其中对于流体方程的正则性研究, Gevrey 类的方法得到广泛的应用.1989年,Foias和Temam创造了Gevrey 正则性方法,并首次使用它来研究具有空间周期性边界条件的Navier-Stokes方程的解析性[8-9].之后,许多作者充分利用这种方法并继续深入挖掘,将其推广到各种泛函空间和方程中.例如,Andrew 和 Edriss[10]研究了一类二维球体上的解析非线性抛物线方程解的正则性. Chueshov和Polatin[11]展示了具有周期性边界条件的广义 Benjamin-Bona-Mahony动力系统的全局吸引子的Gevrey 解析性.
具有分数次耗散项-κΛαv的多孔介质方程由下式给出
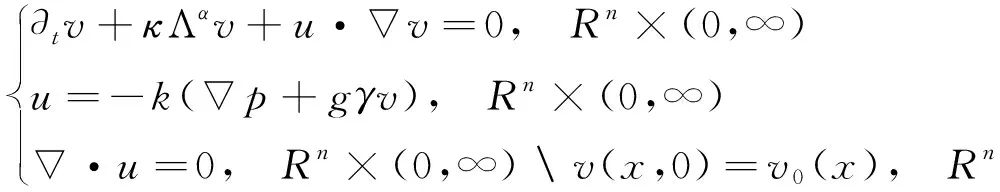
(1)
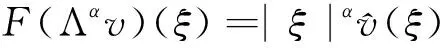
系统(1)可以通过Duhamel原理表示为以下积分方程
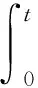
(2)
其中e-κtΛα:=F-1(e-κt|ξ|αF).F表示傅立叶变换,F-1表示傅立叶逆变换.

1 预备知识
首先给出本文提到的符号.对于两个常数A和B,如果存在一个随行变化的常数C使得A≤CB,用记号AB表示.接下来给出关于Littlewood-Paley理论和Fourier-Besov空间的基本结论.
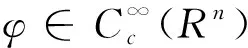
定义以下频率局部化算子:
Δju=φj(D)u=F-1φj(ξ)Fu;Sju=ψj(D)u=F-1ψj(ξ)Fu,
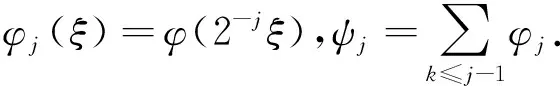
由支集性质易得以下结果,若|i-j|≥2,则ΔiΔjf≡0;若|i-j|≥5,则Δi(Sj-1fΔjg)≡0.通过Bony分解,可将乘积uv分为uv=Tuv+Tvu+R(u,v),并且
定义1 对于s∈R,p,r∈[1,∞],Fourier-Besov空间定义如下,
在这里,当p=∞或q=∞时,范数作通常的改变, 其中P是所有多项式的集合.
定义2 对于0 为了方便证明,将系统(1)写成下面的积分形式 证明首先,要证明 事实上 (3) 接下来证明 (4) 证明为了方便,用B(u,v)表示非线性部分,也就是 接下来,用Δj作用到B(u,v)上,然后做傅立叶变换并取Lp范数,应用Minkowski不等式,得到 ‖F(ΔjB(u,v))‖Lp‖F(Δje-κ(t-τ)Λα(uv))‖Lpdτe-κ(t-τ)2αj‖F(Δj(uv))‖Lpdτ. 根据Bony仿积分解,有 即 ‖F(ΔjB(u,v))‖LpI1+I2+I3. 其中 基于支集的性质,有 对于‖F(Δj(Sj′-1uΔjv))‖Lp,利用Hölder不等式和Young不等式,得到 综上 下面,用同样的方式估计I2. 接下来,估计I3.已知,存在常数N0使得 当1≤p≤2时,利用Hölder不等式和Young不等式,有 当p>2时,仍然可以得到相似的结论, 因此 接着,‖F(ΔjB(u,v))‖Lp关于时间取L∞范数,得到 (5) (6) 下面进一步估计上述方程.首先,用·作用到方程u=-κ(p+gγv)上,再利用自由散度定理·u=0,得到 -Δp=∂nv. 从而解出p并将p带到原式.可得 u=-(-Δ)-1∂nv-γv. 即ui=-RiRnv(i=1,2,…,n-1).un=-RnRnv-v.其中Ri(i=1,2,…,n)表示Riesz变换[14].因此,观察到 ‖ui‖Lp≤C‖v‖Lp,其中1 当‖F(ΔjB(u,v))‖Lp关于时间取L1范数时,得到 (7) (8) 综合式(6)和式(8),引理2得证. 现在证明方程(1)的适定性. 首先,在度量空间Δ={v:‖v‖Xp,r≤Cε,d(v-u):=‖v-u‖Xp,r}(I=[0,∞))上定义一个映射: 对于任意的u,v∈Δ,可以得到 (9) 和 ‖ϑv1-ϑv2‖Xp,r2Cε‖v1-v2‖Xp,r (10) 基于式(9)和(10)的估计,应用标准压缩映射[15],若2Cε≤1,则ϑ是压缩映射.因此,存在v∈Δ使得ϑ(v)=v,则v是方程(1)的唯一解.最后,得到 由上述结果可得,定理1得证. 定理2 对应定理1,在定理1中得到的时间上的全局解满足 利用上述正则性,可进一步获得适度解的长时间衰减估计. (11) 很明显,B(U,V)表示这部分新的非线性项,即 证明由于 因此 由 有 由以上证明可以得到,引理3成立. 证明因为 又 所以 (12) 利用Bony仿积分解,可得 (13) 然后把式(13)代入式(12),利用支集性质,有 ‖F(ΔjB(U,V))‖LpJ1+J2+J3 (14) 其中 (15) 总之 类似地,可以得到 当估计J3时,先考虑 也就是 根据第三部分的结果,得到,当1≤p≤2时, 当p>2时, 通过以上推导,有 ‖F(ΔjB(U,V))‖LpK1+K2+K3+K4. 因为剩下的证明与第三部分对应的相同,证明略.再次利用不动点定理证明定理2,得到 定理3 在定理1的假设下,对任意σ>0,全局解满足下面的时间衰减估计, 其中Cα,σ是独立于α和σ的常数. 根据以上两个公式,有 因此 定理3得证.
2 适定性
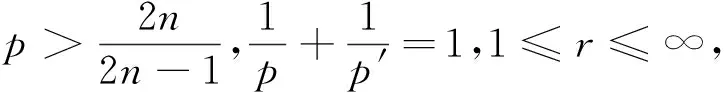
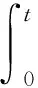



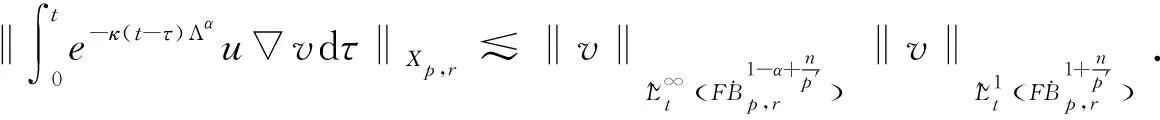
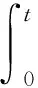
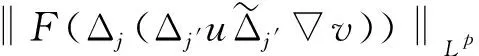
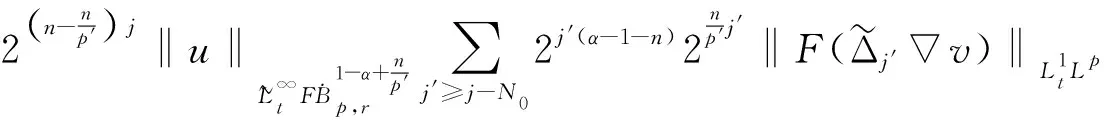
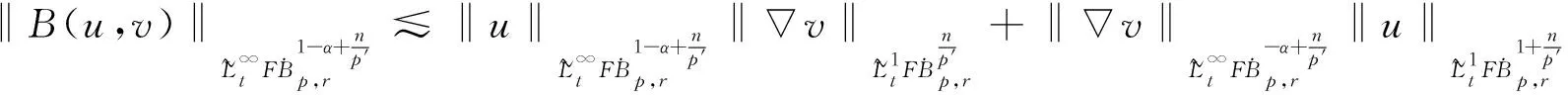
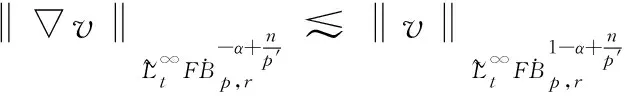

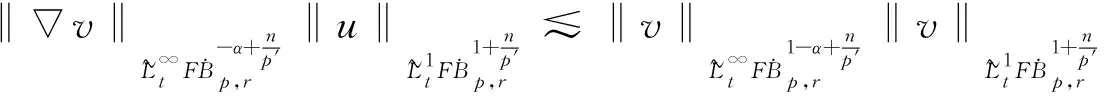
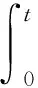
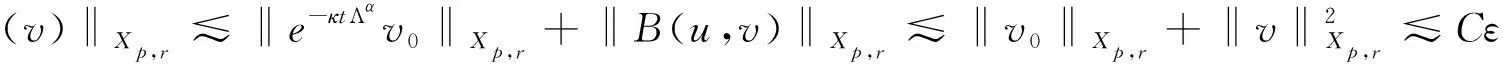
3 Gevrey正则性

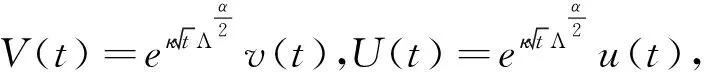
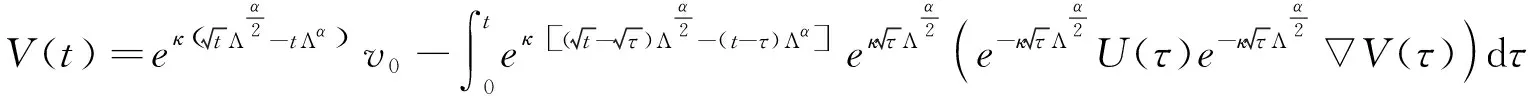


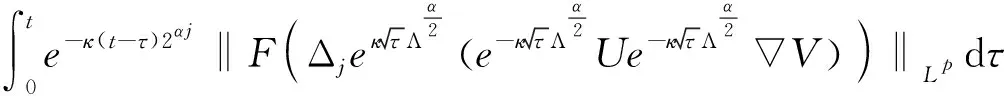
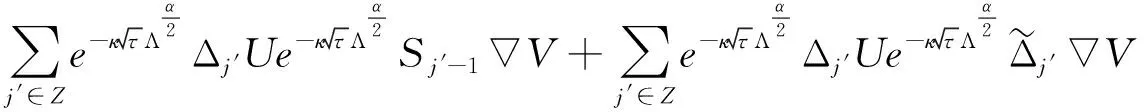
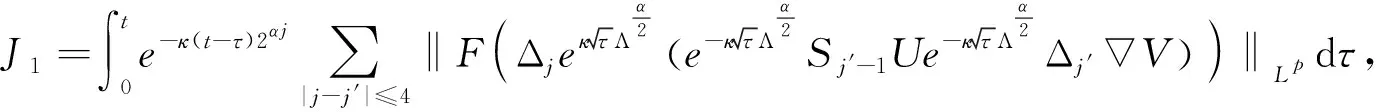
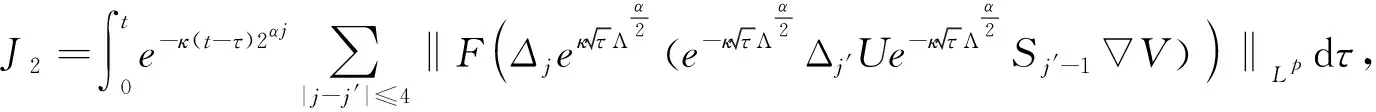
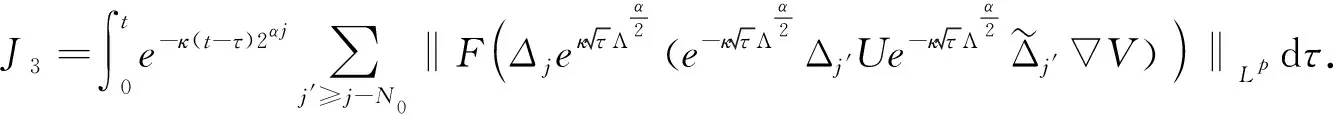

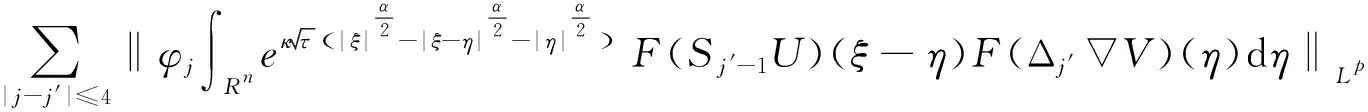
5 适度解的时间衰减