带有p-Laplacian算子的分数阶多点边值问题正解的存在性

解大鹏, 李 东

(1.合肥师范学院 数学与统计学院, 安徽 合肥 230601; 2.佳木斯大学 理学院数学系, 黑龙江 佳木斯 154007)

0 引言

近年来, 分数阶微分方程和带p-Laplacian算子的微分方程成为很多数学工作者的研究热点, 并取得了许多有意义的研究成果[1-6]. Han等利用不动点定理, 得到了如下带有p-Laplacian算子的分数阶微分方程边值问题正解的存在性[1]

其中φ(s)=|s|p-2s,p>1,α∈(2,3],β∈(1,2],f:(0,+∞)→(0,+∞)是连续的.在此研究的基础上,Li等利用不动点定理, 得到了如下带有p-Laplacian算子的分数阶三点边值问题多重正解的存在性[2]，

其中φ(s)=|s|p-2s,p>1,α∈(2,3],β∈(1,2],μ∈[1,α-1),f∈C([0,1]×R+,R+),δ≥0,0<η<1且Δ=1-δηα-μ-1>0.

受上述文献启发,本文将讨论一类带有p-Laplacian算子的分数阶微分方程多点边值问题

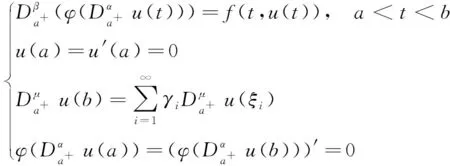
(1)

本文首先找到边值问题相对应的Green函数并讨论其性质,由此得到边值问题(1)的等价积分方程,最后利用不动点定理证明其正解的存在性.

1 预备知识和引理

引理1 假设y∈C[a,b], 则分数阶边值问题

(2)

证明易知问题(2)的通解为

由式(2)的边值条件知C2=C3=0,

故

证毕.

引理2 假设w∈C[a,b], 则分数阶边值问题

(3)

证明易知问题(3)等价于

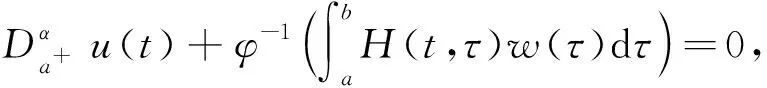
证毕.

引理3G(t,s)和H(t,s)有如下的性质,

(i) 当(t,s)∈[a,b]×[a,b]时, 0≤G(t,s)≤G(b,s);

(ii) 当(t,s)∈I×(a,b)=(3a+b/4,a+3b/4)×(a,b)时,G(t,s)≥(1/4)α-1G(b,s);

(iii) 当(t,s)∈[a,b]×[a,b]时,0≤H(t,s)≤H(s,s);

(iv)当(t,s)∈I×(a,b)=(3a+b/4,a+3b/4)×(a,b)时,H(t,s)≥g(s)H(s,s), 其中

于是,当(t,s)∈[a,b]×[a,b]时,

故, 当(t,s)∈[a,b]×[a,b]时,0=G(a,s)≤G(t,s)≤G(b,s).

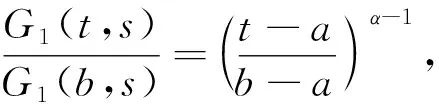
故, 当(t,s)∈I×(a,b)时，

故, 0=H(a,s)≤H(t,s)≤H(s,s), 因此, 当(t,s)∈[a,b]×[a,b]时,

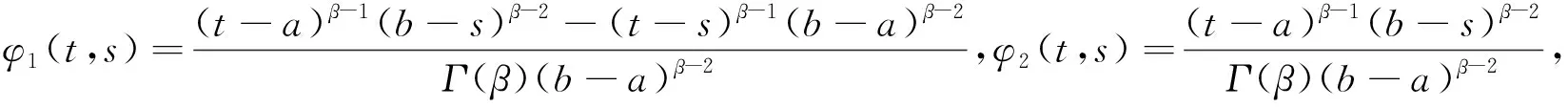
则

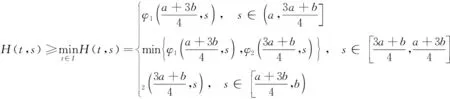
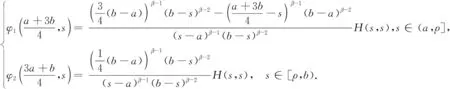
证毕.

2 主要结果

定义算子,

为了方便,引入以下记号:

定理1 若∃r1,r2>0使得r1

(B1)当(t,u)∈[a,b]×[0,r1]时,f(t,u)≥φ(r1N4α-1);

(B2)当(t,u)∈[a,b]×[0,r2]时,f(t,u)≤φ(r2M),

则边值问题(1)至少存在一个正解u,并且满足r1≤‖u‖≤r2.

证明由G,H,f的连续性可知T:K→K是连续的.对于(t,s)∈I×(a,b),u∈K, 由引理3知

这意味着T(K)⊂K.故应用Arzela-Ascoli定理易证算子T:K→K是全连续的.

令Ω1={u∈K:‖u‖≤λ1},对于u∈∂Ω1,由引理3及(B1)知

故, 当u∈∂Ω1时, ‖Tu‖≥‖u‖.

令Ω2={u∈K:‖u‖≤λ2},对于u∈∂Ω2,由引理3及(B2)知

于是,当u∈∂Ω2时,‖Tu‖≤‖u‖.综上,由不动点定理[1]知,分数阶多点边值问题(1)至少存在一个正解u, 并且满足r1≤‖u‖≤r2.

证毕.