浅埋盾构始发地层纵向合理加固长度计算式

晏启祥，陆志明，彭 旸，孙明辉，王新强，雷元亮

（1.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2.中铁建大桥工程局集团有限公司 第二工程有限公司，天津 300300）

目前，城市公共交通不断向地下发展，盾构法在城市轨道交通领域得到越来越广泛的应用。盾构始发是盾构法施工过程中最关键的工序之一，盾构始发破除洞门时端头土体容易失稳滑移，严重时甚至会引发工程事故。因此，盾构施工前必须对始发处土体进行加固，避免土体滑移失稳，但是加固范围过大又会造成资源的浪费。对于实际工程，在确保始发端头土体稳定的前提下，确定合理的土体纵向加固长度就成为该工程的重点问题［1-2］。

目前国内外已有关于盾构始发端头土体加固范围的一定研究。日本JETGROUT 协会［3］基于弹性薄板理论，假定土体为整体板块计算纵向加固范围，并给出始发土体稳定性验算方法。国内曹成勇等［4］基于极限平衡原理，建立盾构进出洞时端头土体稳定性的二维模型，并推导出端头土体纵向加固范围的理论计算式。宋克志等［5］提出1 种由直线和对数螺旋线构成的组合式土体滑移线，基于极限平衡原理对端头土体稳定性进行理论推导，并对其各影响因素进行分析。刘俊杰等［6］考虑洞门破除及盾构动态掘进的影响，基于Midas GTS NX软件研究了盾构始发的合理加固范围及其主要影响因素。吕玺琳等［7］结合村山氏极限平衡法和极限分析上限法，研究了盾构开挖面的稳定性，并分析其各自的影响系数。韦良文［8］研究了泥水平衡盾构的开挖面以及出洞段土体稳定性，综合理论计算和数值模拟2 种方法，分析了始发土体的稳定性以及加固范围。殷黎明［9］建立了砂卵石地层盾构始发土体的四边简支力学模型，推导出土体加固范围的数学解析式，并通过有限元数值模拟对模型进行验证。胡欣雨等［10］结合上海长江隧道工程，基于村山公式，分别对泥水盾构在普通应力状态以及泥浆作用下的土体强度以及开挖面稳定性进行定量研究。丁万涛等［11］结合树木岭隧道始发工程，基于弹性薄板理论计算不同安全系数下端头土体纵向加固范围并利用强度理论和滑移失稳理论进行验算，基于Terzaghi理论计算端头土体横向加固范围，最后结合FLAC3D 进行数值模拟和验证。江华等［12］在现有端头加固模型的基础上，考虑尺寸效应对盾构始发与到达的影响，提出1种改进的端头加固等效荷载模型，并对不同地层的端头加固进行计算对比，验证了端头加固的尺寸效应。王天明等［13］基于盾构端头地层加固理论，对土体的纵向与横向加固范围、洞门密封形式和加固方法进行比选，给出洞门密封型式与地层加固范围的选取方法。雷金山等［14］基于板块强度理论，将砂卵石地层盾构端头土体加固的力学模型简化为四边简支的矩形薄板模型，利用弹性力学中矩形薄板的Levy 解计算出端头土体的纵向加固范围。朱伟等［15］基于拉格朗日有限差分计算程序，研究砂土地层中的盾构开挖面变形和破坏问题，确定了砂土地层盾构开挖面所受压力及其变形。

可以看出，现有的研究成果大都基于弹性薄板理论等理论模型对盾构始发土体的加固范围进行计算，对始发土体滑移失稳模式进行的研究较少，而且目前的研究大都对土体滑移失稳中心的位置进行了简化处理，可能导致计算结果存在一定误差。

在现有研究的基础上，提出1 种改进的对数螺旋线加直线的组合式滑移模式并建立改进后的盾构始发端头土体极限平衡模型（M-SLEM）；对比MSLEM 与既有的端头土体极限平衡模型（SLEM）下，不同安全系数对应的端头土体纵向加固长度；分析2 种模型下隧道埋深、隧道直径、加固土体黏聚力和原状土体内摩擦角4种因素对端头土体纵向合理加固长度的影响以及各影响因素的敏感性；采用数值模拟验证2 种模型下的土体滑移破坏模式和土体加固效果，证实改进模型合理性。

1 改进的端头土体极限平衡模型

1.1 基本假定

使用普通钢筋进行洞门围护结构施工的盾构始发工程，在围护结构破除后掌子面会短暂失去支护，此时端头加固土体在其自重W和地表超载Q的作用下可能达到极限状态，进而发生滑移失稳，造成工程事故，特别是对于浅埋隧道，土体滑移线甚至会从盾构开挖面一直上延至地表处。

在现有土体滑移线理论［2，5，7，16］的基础上，结合日本村山滑动模型，对端头土体滑移线形式进行改进，端头土体组合式滑移线示意图如图1 所示。图中：R0为曲线中心O点与始发处隧道下缘A点之间的距离；Ra为OC间的距离；φ为土体内摩擦角；θ1和θ2分别为OF和OC对应的极角；d为隧道外径；r为BC以上的土体竖向加固距离；H为隧道埋深；ha为O点与地表的竖向距离；L为端头土体纵向加固长度；la和lb分别为O点和C点与始发位置之间的水平距离；σCD，σCF和σAF分别为CD，CF和AF段的法向应力；τCD，τCF和τAF分别为CD，CF和AF段的切向应力，均以图中箭头方向为正方向。

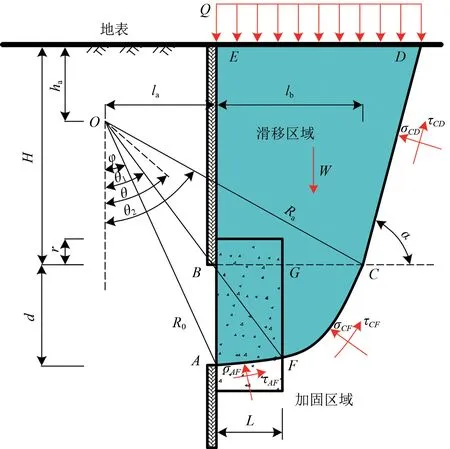
图1 端头土体组合式滑移线示意图

基于现有研究的相关理论和工程实际，做出基本假定如下。

（1）土体滑移线由对数螺旋线AFC和直线BC构成。

（2）对数螺旋线AFC和直线CD的交点C与隧道顶部B位于同一水平线［3，5］，即：BC以下部分土体滑移线为对数螺旋线AFC；BC以上部分，即隧道上方的土体滑移线为直线CD。

（3）对数螺旋线AFC以O点为中心，且曲线在A点与水平面相切，在C点与直线CD相切，满足

（4）对土体破坏角，即直线段CD与水平面的夹角，按文献［8］取为α=

（5）端头土体为均匀介质，对于多层土体采用加权平均法计算其各项参数。

（6）土体的破坏符合Mohr-Coulomb 破坏准则，在土体滑移线上满足

式中：σ为法向应力；τ为切向应力；c为土体黏聚力。

1.2 端头土体的稳定性极限平衡

基于极限平衡原理，在滑移土体达到稳定时，模型整体的下滑力矩和抵抗力矩应该处于平衡状态，由此计算模型中各下滑力矩和抵抗力矩。

1）对数螺旋线几何参数

对于对数螺旋线AFC，由几何关系可得

由式（3）和式（4）解得R0为

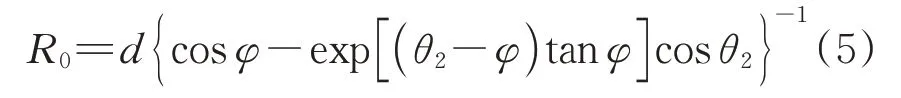
进而，求得图1 中对数螺旋线AFC的各几何参数为

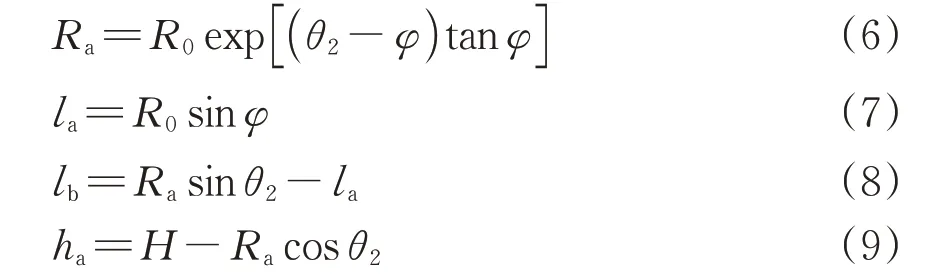
在此基础上，求得端头土体纵向加固长度L与OF的极角θ1之间的关系为

2）下滑力矩

整体模型的下滑力矩主要由土体重力W和地表超载Q引起。地表超载Q对O点的下滑力矩为

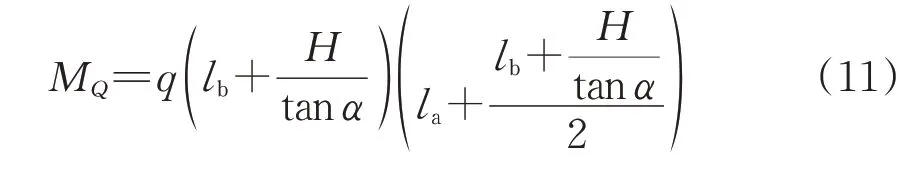
式中：q为地表超载Q的取值。

BCDE部分土体对O点的重力下滑力矩为

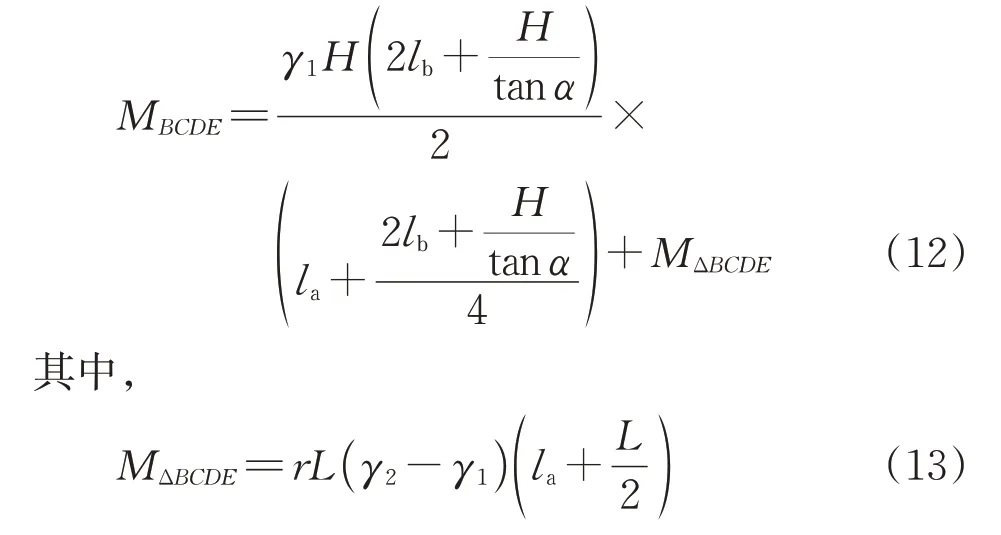
式中：γ1和γ2分别为原始和加固后的土体重度；MΔBCDE为BCDE部分土体加固后对O点的力矩增量（下角标代表加固后的力矩增量，后同）。

基于割补法的原理，计算ABC部分土体对O点的重力下滑力矩为

式中：为假定ABC部分土体全部加固后对O点的下滑力矩；MΔCGF为CGF部分土体加固后对O点的力矩增量。

式中：MΔOCF，MΔOCG和MΔOGF分别为角标对应部分土体加固后对O点的力矩增量。

因此整个区域对O点的重力下滑力矩MG为

3）抵抗力矩

土体滑移线上存在切向和法向的分布力，这些力会对O点产生抵抗力矩，对土体滑移起到阻碍作用。对于图1 中的土体滑移直线CD段和曲线AFC段，土体微元ds的受力状态以及抵抗力矩图示有所不同，直线CD段和曲线AFC段的受力图如图2 所示。由于曲线中CF段和AF段的受力情况一致，仅以CF段为例分析受力。

图2 土体微元受力

在图2（a）中，对于土体滑移直线CD段，由土体微元ds在竖直方向上的受力平衡以及土体破坏准则可得

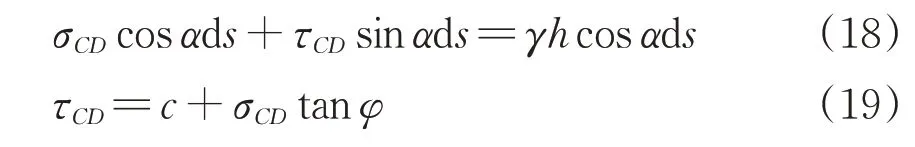
式中：φ为原状土体内摩擦角，对于多层土体采用加权平均法处理。

联立式（23）和式（24），可求得法向应力和切向应力分别为

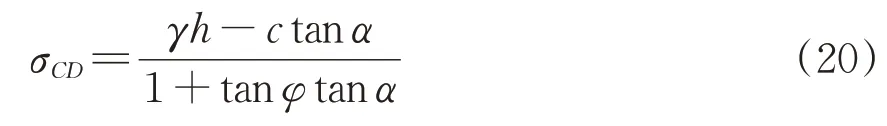
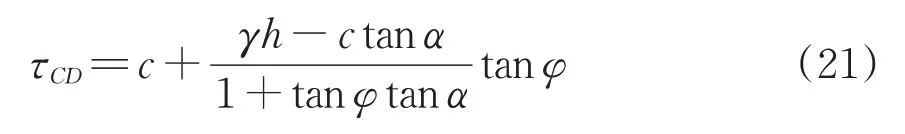
CD段法向压力对O点的抵抗力矩为

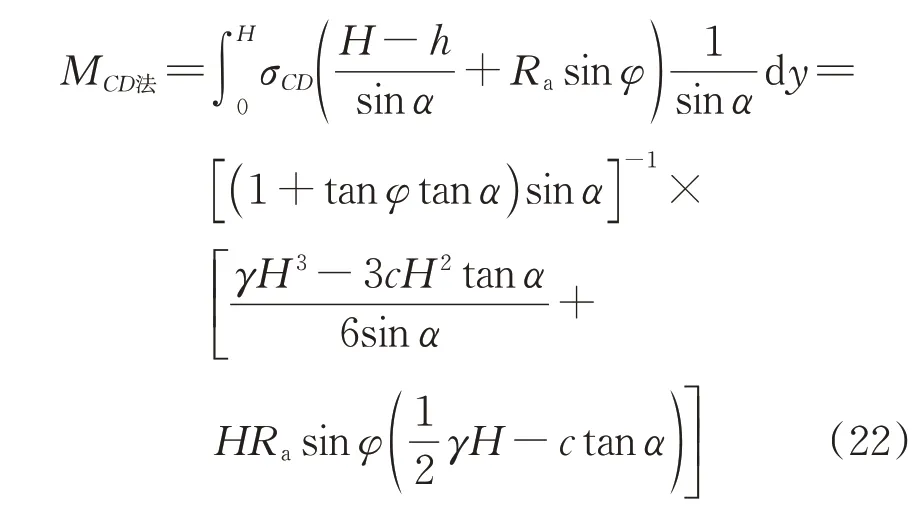
CD段切向剪力对O点的抵抗力矩为

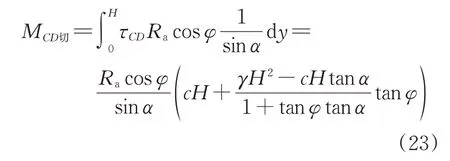
因此，CD段土体滑移线对O点的总抵抗力矩为

在图2（b）中，将土体滑移曲线AFC段进一步分为CF段和AF段，对于CF段，同理可得法向应力和切向应力分别为

CF段法向压力和切向压力对O点的抵抗力矩分别为

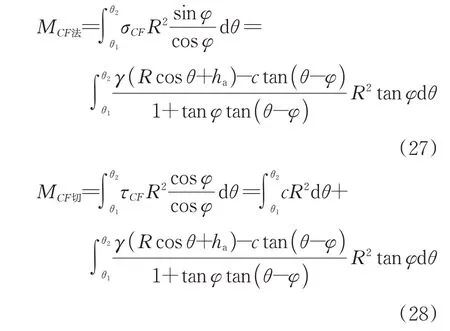
式（28）中第2 部分表达式与MCF法相同，因此，CF段土体滑移线对O点的总抵抗力矩为

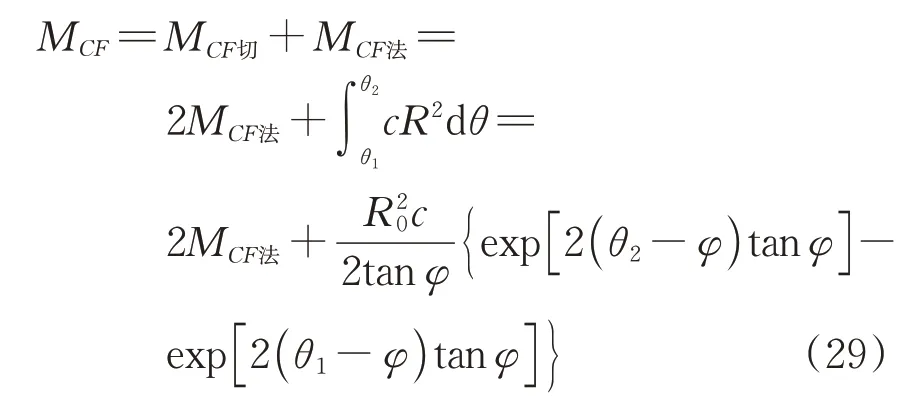
MCF法无显式解析解，可利用编程方法计算数值解。

同理可得，AF段土体滑移线对O点的总抵抗力矩为

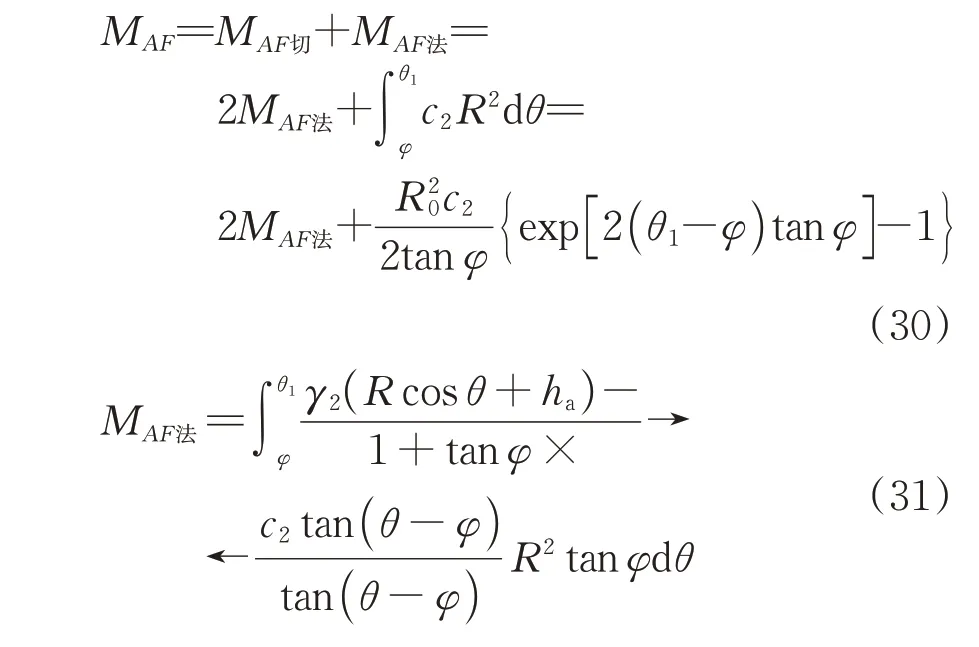
式中：c2和φ2分别为加固土体的黏聚力和内摩擦角。

式（31）中的MAF法也无显式解析解，仍利用编程方法计算数值解。

从表5可以看出，在相同刀具直径下，随着刀具夹持长度增加，即刀具悬伸长度减小时，换能器谐振频率逐渐增大，最大应力值则先减小后增大，这是由于应力集中点从变幅杆处转移到了刀杆根部，而位移节点位置均没有变化，这表明可以通过调整刀具的安装位置来适当改变换能器的谐振频率。

1.3 端头土体纵向合理加固范围

基于土体极限平衡原理，所有外力对O点有力矩平衡

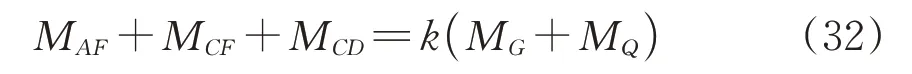
式中：k为工程的稳定安全系数，一般取1.0～2.0。

对于式（32），当安全系数k确定时，可将其与式（10）联立，求得2 个未知数L和θ1，此时求得的L即为端头土体的纵向合理加固长度。

2 加固长度影响因素

2.1 依托工程

以广州地铁18 号线沙溪站盾构始发工程为依托，分别采用本文提出的改进的端头土体极限平衡模型和既有的盾构始发端头土体极限平衡分析模型［16］计算端头土体纵向合理加固长度，并对比不同影响因素引起的变化规律。

沙溪站始发盾构隧道埋深为21.3 m，隧道直径为8.5 m，衬砌厚度为0.4 m。始发处地层从上至下分别为人工填土层、淤泥质细粉砂层、中粗砂层、强风化层和泥质粉砂岩。始发处地层和加固体力学参数见表1。

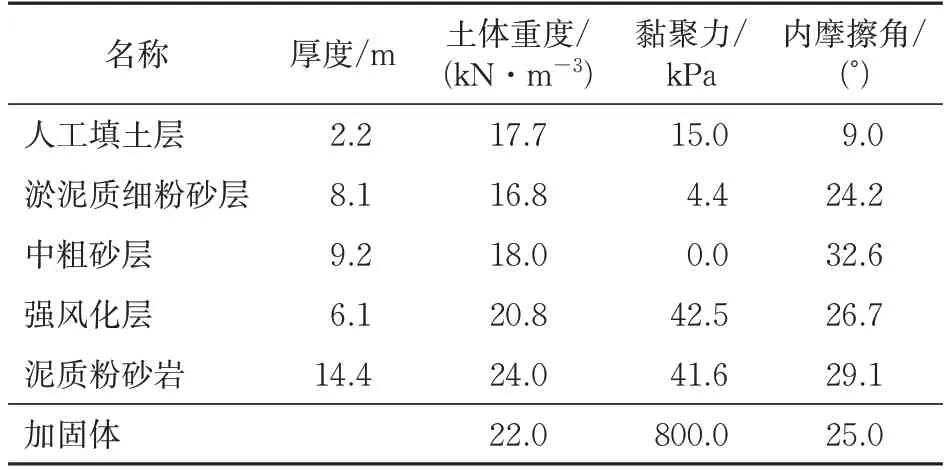
表1 始发地层与加固体力学参数

基于上述工程实例，计算可得沙溪站始发处土体加权平均重度为19.1 kN·m-3，黏聚力为16.8 kPa，内摩擦角为26.8°。该隧道拱顶以上加固距离为2 m；参照相关文章的取值以及工程实况，取地表超载Q为30 kPa。

2.2 纵向合理加固长度计算

根据依托工程土体力学参数的加权平均值与加固体的力学参数，分别基于M-SLEM 与SLEM 这2 种理论模型，编程计算不同安全系数对应的纵向合理加固长度，如图3所示。图中：ΔL为同一安全系数下，2种模型计算得到的纵向加固长度差值。

图3 不同安全系数对应的端头土体纵向合理加固长度

由图3 可知：随着安全系数不断增大，2 种理论模型计算所得的纵向合理加固长度均不断增大，但增大的趋势有所不同；按照SLEM 计算，纵向合理加固长度随安全系数增加呈现线性增加的趋势，而按照M-SLEM 计算，这一变化趋势是非线性的；ΔL随安全系数增加呈现先增加后减小的变化规律，安全系数为1.0 时L值最低，为0.4 m，安全系数为1.6时ΔL值最大，为2.4 m，安全系数大于1.6 后ΔL值又逐渐减小，说明2 种模型的计算结果存在较大差距，按照SLEM 的结果求得的纵向加固长度明显偏小，有可能无法满足工程的安全性要求。

在工程实践中，计算端头土体纵向加固长度时一般取安全系数为1.5～2.0，本文依托工程取1.5。参考M-SLEM 计算结果并结合现场实际情况，当纵向加固长度取12.8 m时，可实际施工过程中取得良好的加固效果；同一工程在同样条件下，根据SLEM 计算得到的端头土体纵向加固长度仅为9.7 m，与前者差值达2.1 m，可能会导致土体失稳进而影响施工安全。

2.3 影响因素

在实际工程中，隧道埋深、隧道直径、原状土体黏聚力及内摩擦角、加固土体黏聚力等因素会影响土体滑移失稳模式，进而影响端头土体的纵向合理加固长度。由于原状土体黏聚力与加固土体黏聚力在数值上相差很大，对端头土体纵向加固长度的计算影响较小，因此仅考虑隧道埋深、隧道直径、加固土体黏聚力和原状土体内摩擦角这4种主要影响因素，按安全系数分别取1.0，1.5 和2.0 的情况进行计算后，分析2 种模型下不同影响因素对应的端头土体纵向合理加固长度变化规律。

1）隧道埋深

2 种模型下，端头土体纵向合理加固长度与隧道埋深间的关系如图4 所示。由图4 可知：纵向合理加固长度随隧道埋深的变化规律基本一致，埋深越大，纵向合理加固长度越大，且两者近似呈线性关系，这是因为埋深增大会导致上覆土体的重力下滑力矩增大，为保证土体的极限平衡，需要增大纵向合理加固长度以提供更大的抵抗力矩；安全系数为1.0时，2 种模型得到的结果基本一致，但当安全系数增至1.5 和2.0时，M-SLEM 得到的计算结果更大。

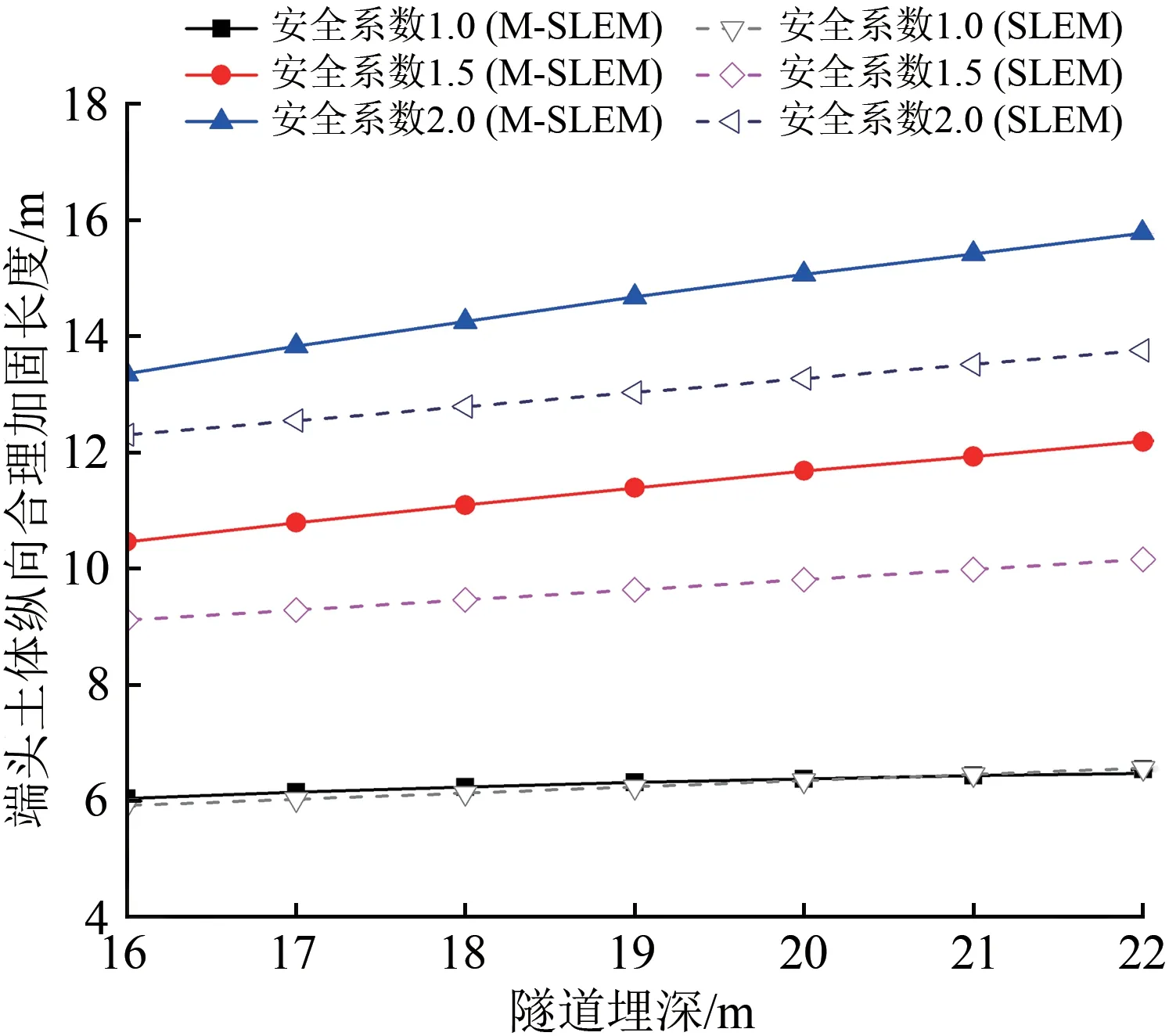
图4 端头土体纵向合理加固长度和隧道埋深的关系

需要说明的是，本文模型主要针对浅埋盾构隧道，当隧道埋深过大时，在土拱效应等因素的作用下，端头土体滑移失稳的区域可能不会延伸至地表处，与前述基本假定不符，此时本文的土体滑移模式不再适用。

2）隧道直径

2 种模型下，端头土体纵向合理加固长度与隧道直径间的关系如图5 所示。由图5 可知：与隧道埋深的影响类似，隧道直径越大，纵向合理加固长度越大，且这两者也近似呈线性关系，这是因为隧道直径是滑移线几何形状的重要决定因素，直径增大会导致滑移线整体向外扩大，进而导致上覆土体的重力下滑力矩增大，因此需要增大纵向合理加固长度以提供更大的抵抗力矩；安全系数为1.0 且隧道直径较小时，2 种模型的计算结果相差较小，但其他情况下M-SLEM的计算结果均更大。

3）加固土体黏聚力和原状土体内摩擦角

2 种模型下，端头土体纵向合理加固长度与加固土体黏聚力、原状土体内摩擦角间的关系分别如图6和图7所示。由图6和图7可知：纵向合理加固长度随加固土体黏聚力和原状土体内摩擦角的变化规律基本一致，黏聚力和内摩擦角越大，纵向合理加固长度越小，且近似呈线性关系，这是因为土体黏聚力和内摩擦角的增大意味着土体强度提升，可以提供更大的抵抗力矩，因此施工时一定要保证土体加固的质量，这是保证始发土体稳定性、确保工程安全性最有效的措施之一；安全系数为1.0时，2 种模型的计算值基本一致，当安全系数增至1.5和2.0时，M-SLEM的计算结果更大。

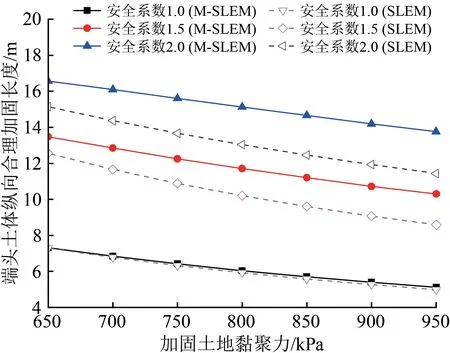
图6 端头土体纵向合理加固长度和加固土体黏聚力的关系

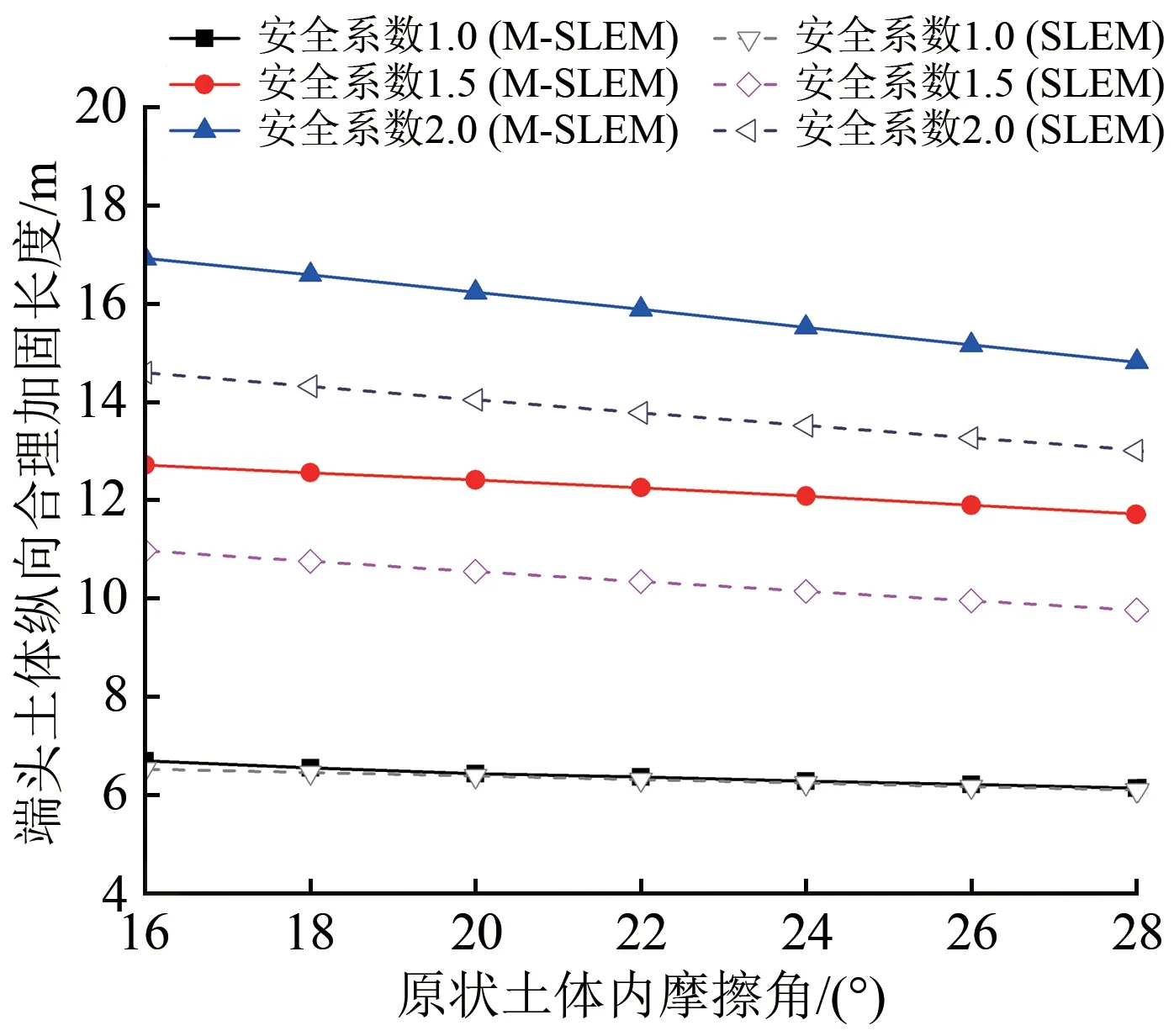
图7 端头土体纵向合理加固长度和原状土体内摩擦角的关系

总体而言，隧道埋深和隧道直径越小、土体内摩擦角和加固土体黏聚力越大时，能够满足施工安全的端头土体纵向加固长度越小；同时，安全系数增大会导致所需的端头土体纵向加固长度显著提高。

2.4 敏感性分析

利用敏感度函数对各影响因素开展敏感性分析，敏感度函数值越大，说明系统特性对该影响因素越敏感。以端头土体纵向加固长度L为系统特征，以隧道埋深H、隧道直径d、加固土体黏聚力c2和原状土体内摩擦角φ为影响因素，得到敏感度函数L的系统特征模型及其敏感度函数Li分别为

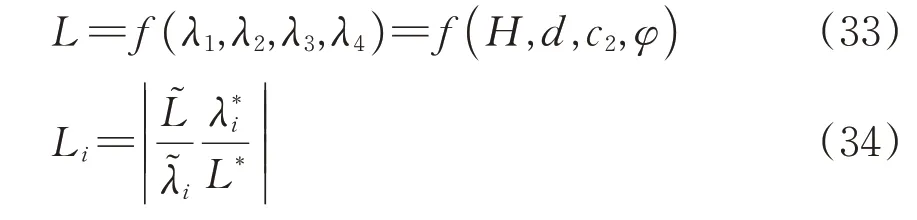
式中：λi为决定系统特性的影响因素，i=1,2,3,4；L*和分别为基准状态下的系统特征和影响因素取值；和分别为系统特征和影响因素的改变量。

仍取安全系数为1.5，以纵向加固长度12.8 m、隧道埋深21.3 m、隧道直径8.5 m、加固土体黏聚力800 kPa、原状土体内摩擦角26.8°为基准状态，计算得到各影响因素的敏感度函数值见表2。

表2 各影响因素的敏感度函数值

由表2 可知：各影响因素对端头土体纵向加固长度的敏感性并不一致，最敏感因素是隧道埋深H，敏感度函数值达到1.255，其次是加固土体黏聚力c2，敏感度函数值为0.971，最不敏感的是隧道直径d和原状土体内摩擦角φ；隧道埋深和加固土体黏聚力对端头土体纵向加固长度的影响更大，在施工过程中应该重视端头土体的加固质量，以获得足够的黏聚力保障加固效果。

3 数值模拟及加固效果对比

根据前文的计算，安全系数在1.5～2.0时，2种模型下端头土体纵向合理加固长度的差值较大，有必要对加固效果进行对比分析。为此，采用FLAC3D有限差分软件，参照前述工程实例建立土体加固数值模型，盾构直径8.5 m，埋深21.3 m，模型高60 m，地连墙厚1 m，隧道端部土体长68 m（取盾构直径的8 倍），如图8 所示。图中：以模型左下角土体处为原点；以水平方向为x轴，取掘进方向为正；竖直方向为y轴，取上方为正。土体采用Mohr-Coulomb 模型，地连墙和加固体采用弹性模型，参数取值与表1一致。

图8 FLAC3D数值模型（单位：m）

3.1 土体滑移线

经过FLAC3D软件计算，得到未加固工况下始发处土体的位移矢量图，并与M-SLEM 与SLEM这2种模型下的计算结果进行对比，如图9所示。

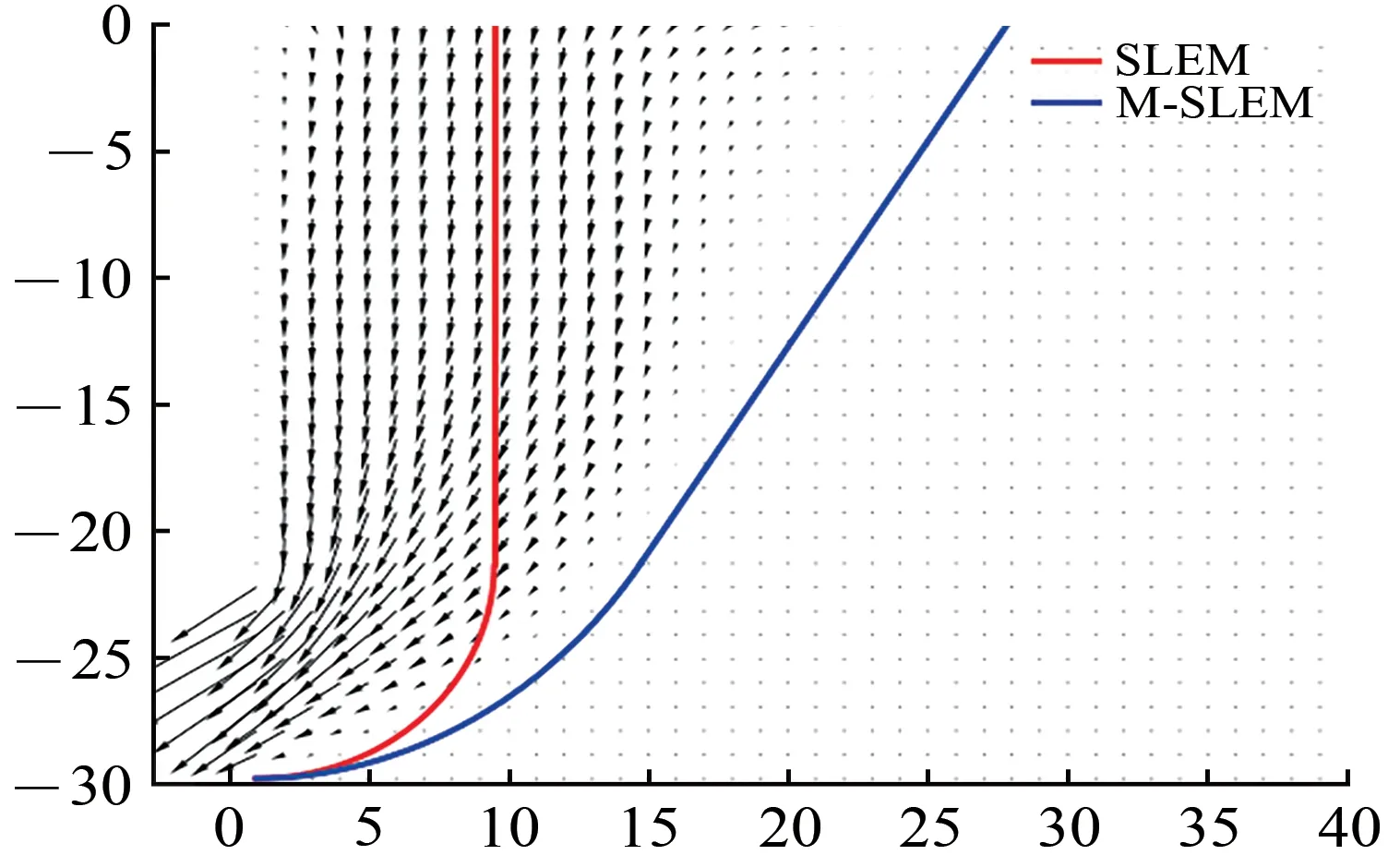
图9 始发处土体位移矢量图

由图9 可知：按照M-SLEM 求得的滑移线与数值模拟结果吻合度较高，能够包络滑动土体区域；按照SLEM 求得的滑移线则明显低估了土体的滑动范围，导致下滑力矩的计算值偏小，进而导致计算出的端头土体纵向加固长度偏小；采用MSLEM 计算端头土体纵向合理加固长度能够更好地保障工程安全。

3.2 土体应力应变

为分析2 种模型下不同纵向加固长度时端头土体的加固效果，仍取安全系数为1.5，基于2 种模型求得纵向加固长度分别为9.7和12.0 m，绘制相应的剪应力云图和剪应变云图分别如图10 和图11所示。

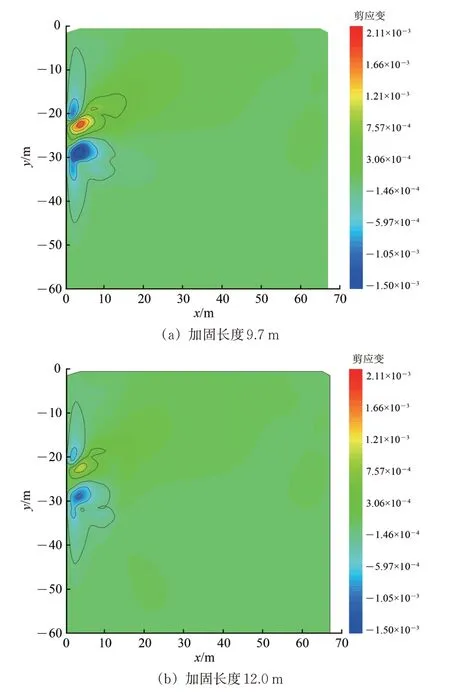
图11 土体剪应变云图

由图10 可知：不同端头土体纵向加固长度下，土体剪应力云图分布形式整体近似，洞门底部前方的较小区域以及洞门顶部前方的较大区域分别为负剪应力和正剪应力的极值区；端头土体纵向加固长度从9.7 m 增至12.0 m时，剪应力最大值从5.99×104Pa 降至4.70×104Pa，剪应力极值的分布区域也有所减小；采用M-SLEM 计算所得的端头土体纵向加固长度更能减小土体剪应力，进而进一步减小具有滑移趋势的土体范围，提高土体加固的效果。

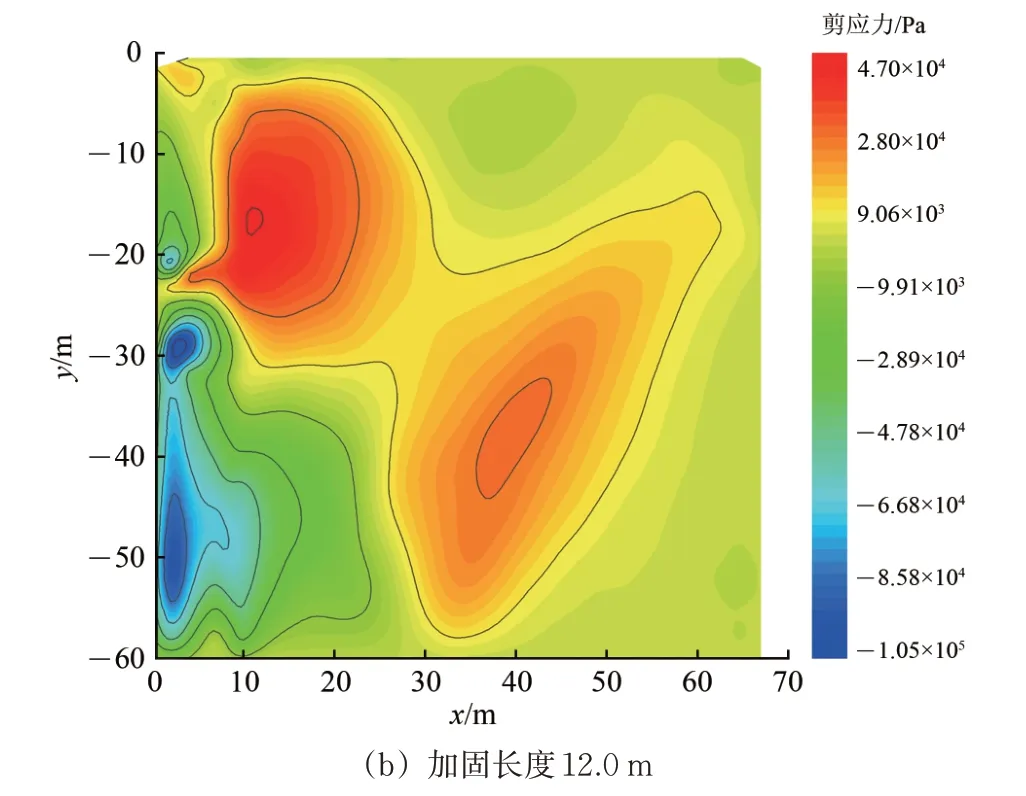
图10 土体剪应力云图

由图11 可知：不同端头土体纵向加固长度下，土体剪应变云图分布形式也整体近似，洞门底部前方区域以及洞门顶部上侧的局部区域为负剪应变极值区，洞门顶部前方区域为正剪应变极值区；端头土体纵向加固长度从9.7 m 增至12.0 m时，剪应变极值区的分布范围明显减小，且负剪应变和正剪应变的最值分别从-1.50×10-3和2.11×10-3降至-1.02×10-3和1.17×10-3；较SLEM，采用M-SLEM 计算所得的端头土体纵向加固长度可大幅度减小土体剪应变数值以及应变区分布范围，有效提高土体稳定性。

3.3 土体加固效果

土体的位移是土体力学状态的直观反映，加固土体向端头井的位移可在一定程度上反映加固效果，即：加固土体向端头井的位移越大，土体应力场的量值越大，土体应力状态越靠近失稳临界状态，表明相对加固效果越差。鉴于目前尚未有明确的指标评价端头土体加固后的稳定性，定义端头地层稳定系数ζ，用于评价土体的相对加固效果。

式中：ζi为不同加固长度对应的端头地层稳定系数；xi为不同工况下洞门始发处盾构圆心位置土体的水平位移值，mm。

按式（35），取盾构始发洞门处土体水平位移的倒数并对其进行归一化处理，然后得到端头地层稳定系数ζ与加固长度的关系如图12所示。

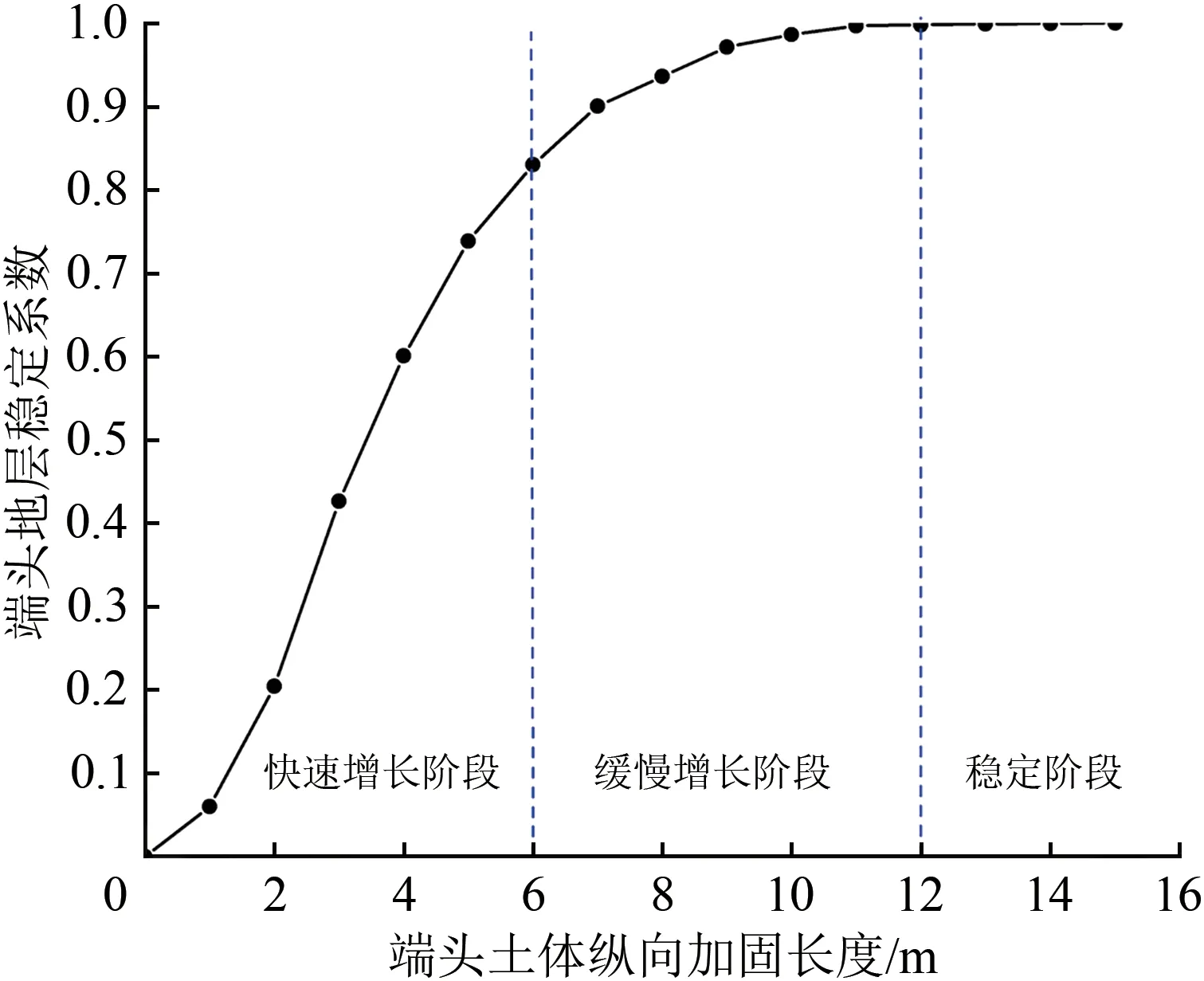
图12 ζ与加固长度的关系

由式（35）和图12 可知：稳定系数越大，土体的相对加固效果越好；在一定的地层力学参数下，端头地层稳定系数随端头土体纵向加固长度的变化趋势可大致分为快速增长—缓慢增长—稳定共3 个阶段；在快速增长阶段，随着端头土体纵向加固长度的增加，其稳定系数急剧增大，此阶段土体的相对加固效果受端头土体纵向加固长度的影响较为显著；在缓慢增长阶段，随着端头土体纵向加固长度的增加，端头地层稳定系数仍在增大，但增长率逐渐放缓，端头土体纵向加固长度对端头地层稳定系数的影响逐渐减弱；在稳定阶段，随端头土体纵向加固长度的增加，其稳定系数几乎不再变化，端头土体纵向加固长度的增加对加固效果无实质性影响。

地层加固长度存在可兼顾工程安全性与经济性的最优取值范围。对本文依托工程，当端头土体纵向加固长度超过12.0 m 之后，加固效果的增长率低于1%。因此当端头土体纵向加固长度取为12.0 m 左右时，不仅能确保端头土体稳定性，还能兼顾工程经济性，这与M-SLEM 的计算结果更接近。依托工程参考本文的理论计算结果并结合自身实际情况，取端头土体纵向加固长度为12.8 m，得到了良好的加固效果。

4 结论

（1）对浅埋盾构的始发端头土体滑移线形式进行改进，建立1种对数螺旋线加直线的组合式滑动模式；采用M-SLEM 计算得到的浅埋盾构始发端头土体纵向合理加固长度随安全系数的增加，呈非线性增加趋势。

（2）对于浅埋盾构始发工程，隧道埋深和隧道直径越小、加固土体黏聚力和原状土体内摩擦角和越大时，所需的端头土体纵向加固长度越小，且端头土体纵向加固长度与各影响因素近似呈线性关系。这4个主要影响因素对端头土体纵向合理加固长度的敏感性也不一致，隧道埋深和加固土体黏聚力对加固长度的影响相对更大，在施工过程中应该重视端头土体的加固质量，以获得足够的黏聚力保障加固效果。

（3）依托广州地铁18 号线沙溪站盾构始发工程，采用M-SLEM 计算得到的滑移线与数值模拟结果吻合度较高，能够包络滑动土体区域；采用SLEM 计算得到的滑移线则明显低估了土体的滑动范围，导致下滑力矩的计算值偏小，进而导致计算出的加固长度偏小。采用M-SLEM 计算端头土体纵向加固长度，能够更好地保障工程安全。

（4）随着稳定系数的变化，可将浅埋盾构端头土体的纵向加固长度分为快速增长阶段、缓慢增长阶段和稳定阶段3个阶段，综合考虑工程安全与经济性，这一加固长度存在最优值。实际工程参考本文的计算结果，取端头土体纵向加固长度为12.8 m、对应安全系数为1.58 时获得良好的加固效果，不仅能确保端头土体稳定性，还能兼顾工程经济性。