非线性三阶方程三点边值问题解的存在性和唯一性

王国灿

(大连交通大学 理学院，辽宁 大连 116028)

三阶非线性微分方程的三点边值问题在常微分方程理论研究中有一定的积极意义，同时在工程物理学中有很多应用[1-4]，但工作重点主要是分析特殊的非线性方程与线性边值问题，而且对于解的唯一性的研究并不多.本文利用上下解理论[5-8]，讨论以下一般的三阶非线性三点边值问题:

x‴=f(t,x,x′,x″)

(1)

(2)

本文将在普通意义下研究问题(1)与(2)的解的存在性、唯一性.

1 辅助引理

下面考虑一类二阶积分微分方程的非线性边值问题

u″=f(t,Tu,u,u′)

(3)

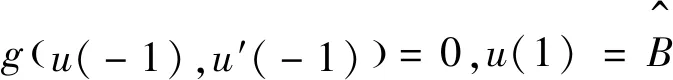
(4)

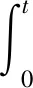
定义1 如果给定的函数β(t)和α(t)∈C2[-1,1]，在[-1,1]上使得α(t)≤β(t)，β″(t)≤f(t,[Tβ](t),β(t),β′(t))，α″(t)≥f(t,[Tα](t),α(t),α′(t))，则称β(t)和α(t)为方程(3)的上解与下解.

引理1如果满足下列条件：

(1)引理1中的(1)，(2)成立；

(2)g(ξ,η)∈C(R2)，且g(ξ,η)对固定的ξ关于η单调不减；

(3)方程(3)有上解β(t)和下解α(t)，且

g(α(-1),α′(-1))≥0，

g(β(-1),β′(-1))≤0，

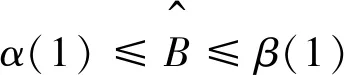
则边值问题(3)、(4)有解u(t)，使得α(t)≤u(t)≤β(t)，-1≤t≤1.

证明：利用迭代法构造序列及一致有界同等连续原理，可得定理为真.

引理2如果满足下列条件

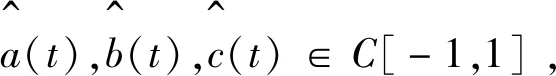
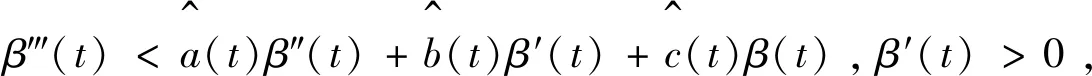
则边值问题

(5)

ay′(-1)+by″(-1)=0,

y(0)=0,y′(1)=0

(6)

只有零解.

证明：利用反证法构造与结论矛盾的结果，可知引理成立.

2 主要结果

下面将讨论边值问题(1)、(2)解的存在性与唯一性.

定义2 如果存在函数β(t)和α(t)∈C3[-1,1]，使得当-1≤t≤1时，α′(t)≤β′(t)，β‴(t)≤f(t,β(t),β′(t),β″(t))，α‴(t)≥f(t,α(t),α′(t),α″(t))，且当-1≤t≤0时，

β(t)≤α(t)，当0≤t≤1时，α(t)≤β(t)，则称β(t)和α(t)为方程(1)的上下解.

如果函数f(t,x,x′,x″)满足下列两个条件之一，则称方程(1)具有三阶Nagumo条件：

(a)对任何的正数N，存在正函数h=h(N)，使得(t,x,x′,x″)∈[0,1]×[-N,N]×R2成立时|f(t,x,x′,x″)|≤hΦr1(|x′|)Φr2(|x″|)，其中0≤r1≤1，r2>0，r1+r2≤3，且Φr(l)=max{1,lr},r>0，0≤l≤+∞；

(b)对任何的(t,x,x′)∈[0,1]×R2使得f(t,x,x′,x″)=O(|x″)|2)，|x″|→∞.

定理1如果下列条件满足

(1)f(t,x,x′,x″)∈C([-1,1]×R3)，符合Nagumo要求，且当-1≤t≤0时，关于x单调不减；当0≤t≤1时，关于x单调不增；

(2)引理2中的(2)成立；

(3)方程(1)存在上下解β(t)和α(t)，且

则边值问题(1)，(2)存在解x(t)∈C3[-1,1]，不等式β(t)≤x(t)≤α(t),-1≤t≤0，α(t)≤x(t)≤β(t),0≤t≤1成立.

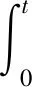
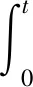
(1)′

g(u(-1),u′(-1))=0,u(1)=B

(2)′

又由x(t)构造得到

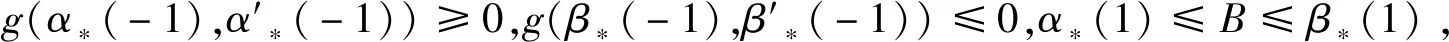
定理2如果下列条件满足

(1)定理1中的(1)，(2)成立;

(2)存在函数β(t)∈C3[-1,1]，当-1≤t≤1时,0<β′(t),0<β″(t)，β‴(t)≤fx″(t,x,x′,x″)β″(t)+fx′(t,x,x′,x″)β′(t)+fx(t,x,x′,x″)β(t)，且当-1≤t≤0时，β(t)≤0，当0≤t≤1时，0≤β(t)，β(0)=0；

(3)对任意ξ,η∈(-∞,+∞)，满足gξ(ξ,η)β′(-1)+gη(ξ,η)β″(-1)<0；

则边值问题(1)、(2)有唯一解.

证明：利用反证法.如果边值问题(1)、(2)存在两个相异的解x1(t)，x2(t)，记y(t)=x2(t)-x1(t)，则y(t)应满足下述边值

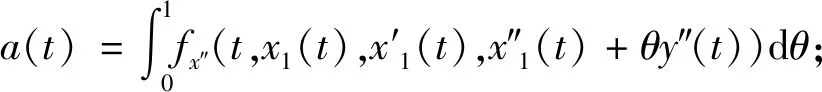
由条件(1)知，a(t),b(t),c(t)于-1≤t≤1上连续，且c(t)≥0,-1≤t≤0，c(t)≤0,