具非线性对流项热传导方程的有限差分法

张继红，栾舒含，梁波

(大连交通大学 理学院，辽宁 大连 116028)

本文考虑如下带有初边值条件的具非线性对流项主部为热传导算子的对流扩散方程：

(1)

式中:x∈(a,b);t∈(0,T);指数p是参数.

许多物理现象，比如液体薄片在重力作用下的运动情况，流体在多孔介质中流动等都与方程(1)有关.Kamin[1]证明了不带对流项的标准渗流方程源型解的存在唯一性；Brezis等[2]给出了具有吸收项的热传导方程测度初值问题解的存在性；卢国富证明了具非线性对流项主部为热传导算子的对流扩散方程的源型解[3].

近年来，对这类非线性偏微分方程的数值求解[4]也取得了很大进展，尤其是与Matlab软件相结合，借助Matlab的数值计算和图形处理技术[5]，使得非线性偏微分方程解的意义更好理解.

本文主要研究具非线性对流项热传导方程的有限差分法实现，重点研究当参数p变化时，对方程的数值解会产生怎样的影响.

1 有限差分法

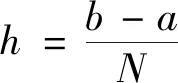
考虑内网点(xk,tn)处，原方程成立：

ut(xj,tn)-uxx(xj,tn)+|ux(xj,tn)|p=f(xj,tn)

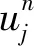
整理可得

(2)

与初边值条件相应的差分方程为：

(3)

方程(2)与(3)联立，即为与方程(1)相对应的差分方程.

2 数据实验与结果分析

对具非线性对流项热传导方程(1)，用差分格式(2)、(3)进行数值计算，区间设为[0,π]，空间步长、时间步长分别取h=π/30、τ=0.001.

下面针对具体例子给出相应的数值实验，重点研究参数p对差分解的影响情况.

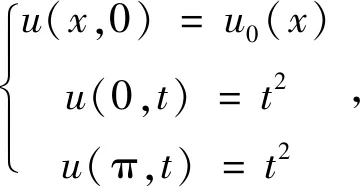
当参数p=1，时刻T=1时，可以得到相应的差分解，并与方程(1)的真实解u(x,t)=t2+sinx进行比较，得到的图像分别如图1～图3所示.图1为p=1，T=1时相应的数值解与真实解的对比图，图中可以看出数值解完全落在真实解的曲线上.图2为p=1，时间t在[0,1]变化时的三维动态数值解模拟图.图3为p=1，时间t在[0,1]变化时的数值解与真实解绝对误差图.图中可以看到绝对误差不超过0.012，也就是说局部截断误差可以达到O(h2).

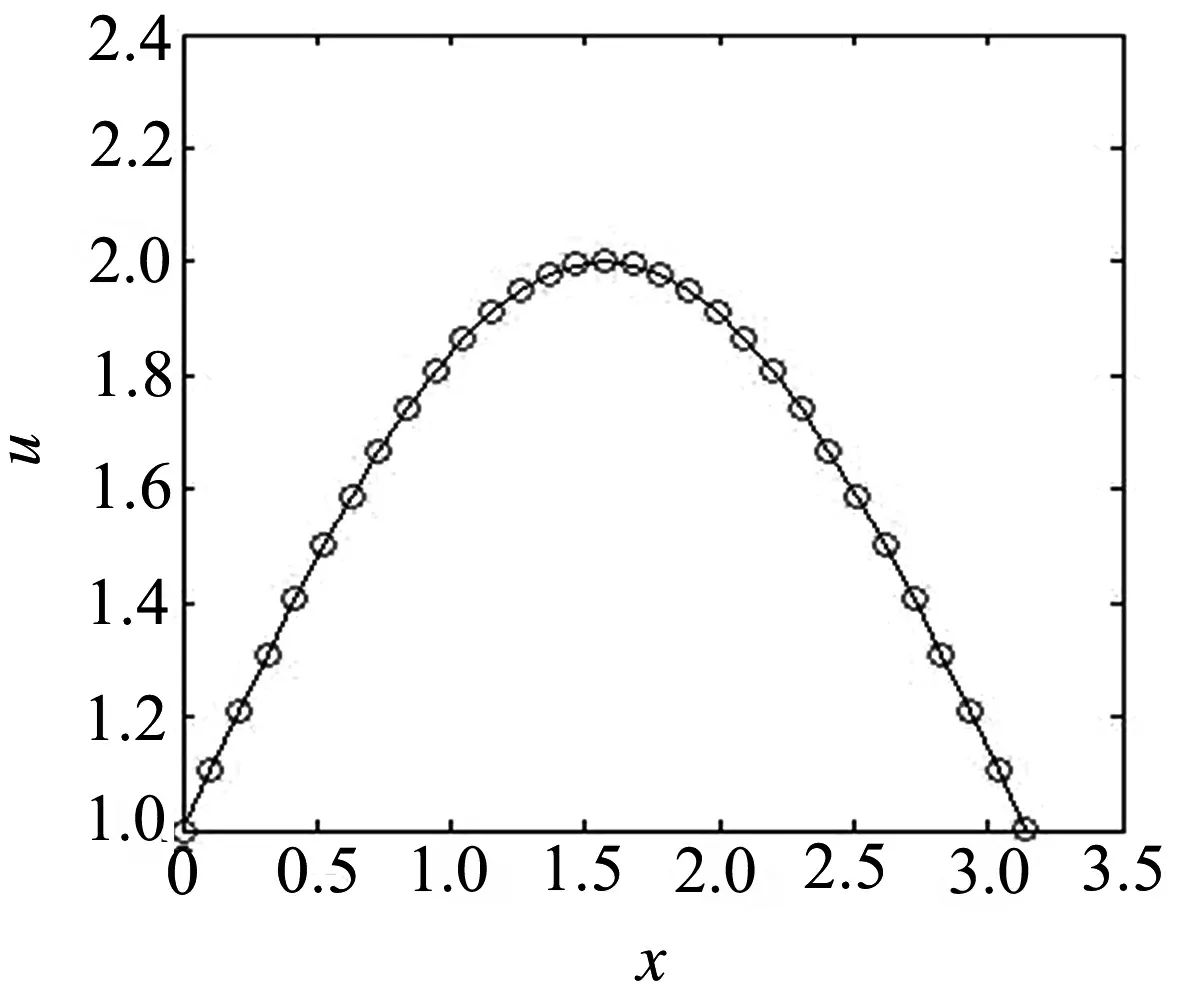
图1 数值解与真实解对比图

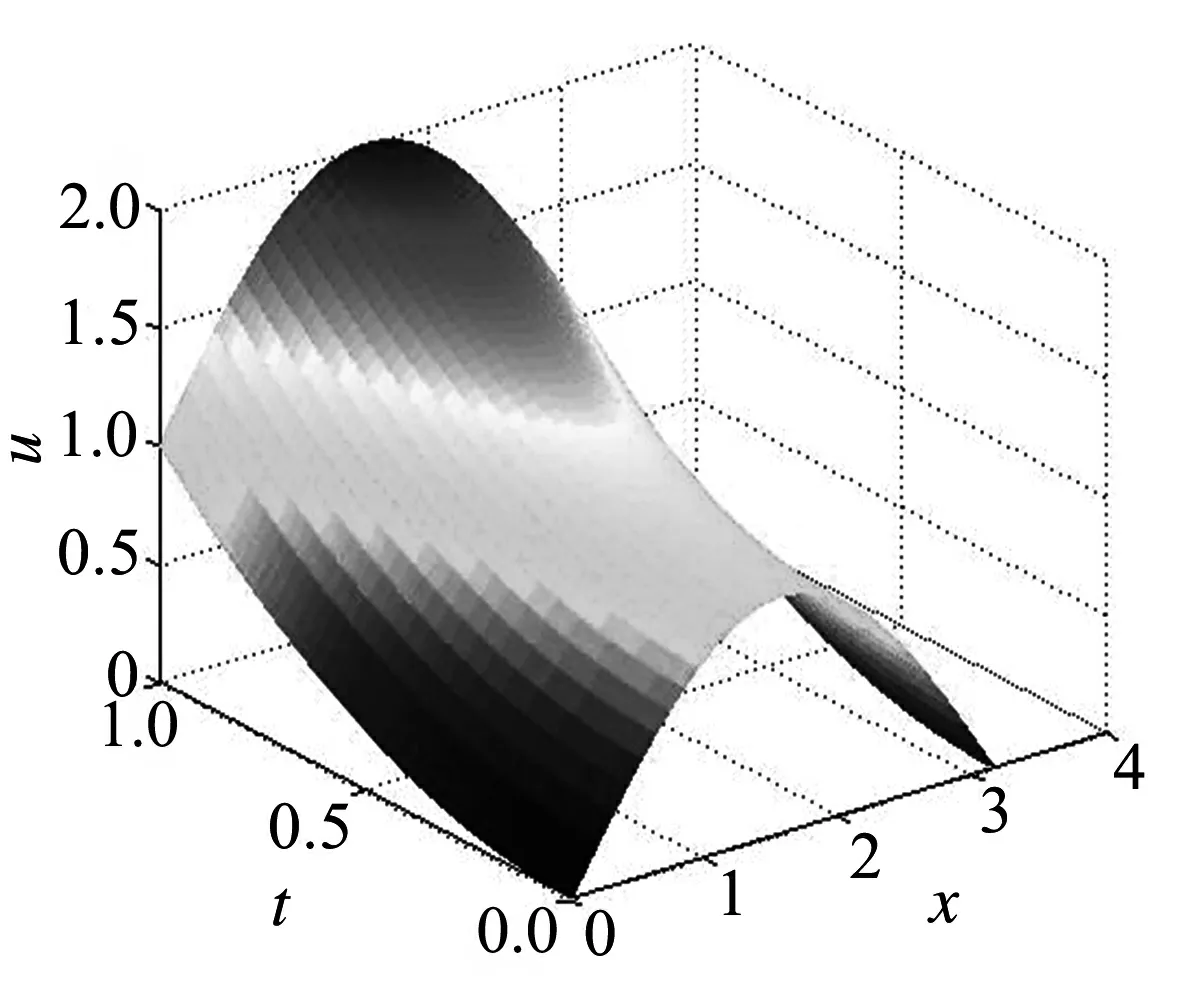
图2 数值解三维图像

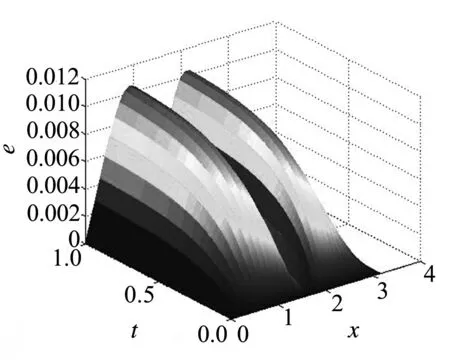
图3 数值解与真实解绝对误差三维图

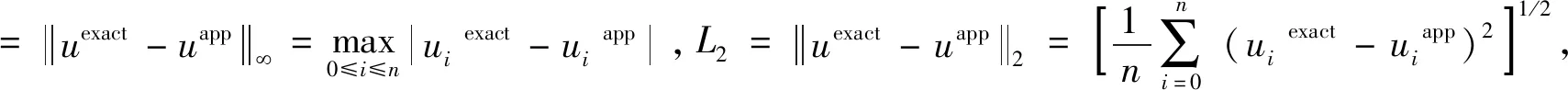
表1、表2分别给出了取不同参数p时，不同时刻T相应的误差范数对比表.表1给出了p>1时，不同时刻T相应的误差范数情况；表2给出了p<1时，不同时刻T相应的误差范数情况.由表1可以看出，当p>1，L∞,L2数量级基本稳定在O(h2)时，当p发生变化，误差并没有明显增长，且随着时刻T的增加，误差也没有明显增长，数值结果保持稳定.由表2可以看出，当p<1，L∞,L2数量级也基本稳定在O(h2)时，当p发生变化，误差数量级没有明显增长，但是随着参数p的变小，尤其是p=0.1时，误差范数随时间变化较大，两种误差范数都明显增大，不能保持数值结果的稳定性.

表1 p>1时在不同时刻T相应的误差范数对比表

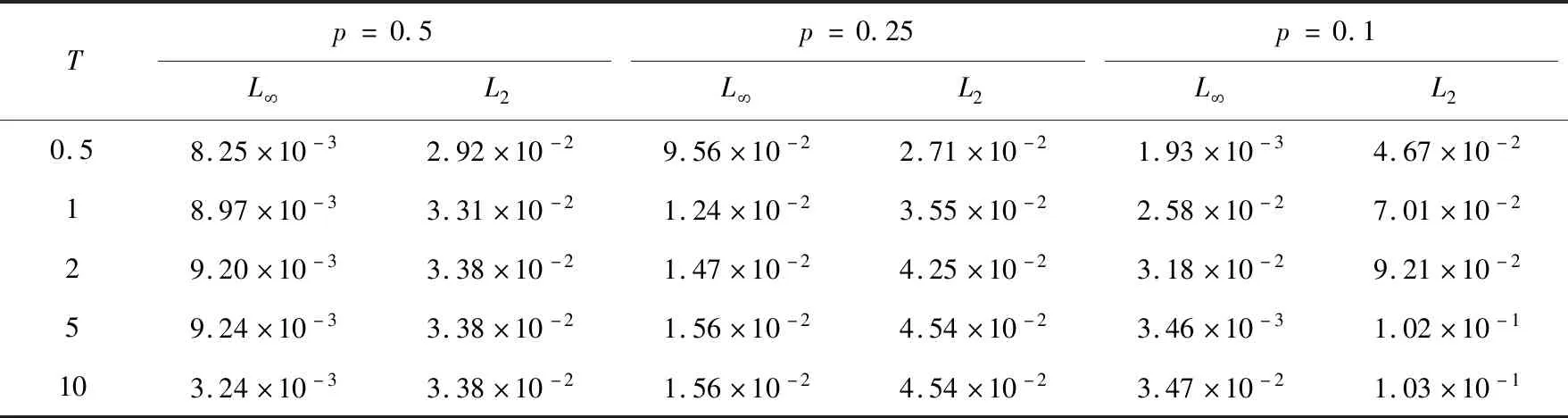
表2 p<1时在不同时刻T相应的误差范数对比表

3 结论

具非线性对流项热传导方程具有一定的研究意义，对其进行数值计算可以更加方便地研究和解决实际问题.本文引入了具非线性对流项热传导方程的有限差分法，通过具体算例，探讨了当参数p发生变化时，相应的差分解是否会发生改变的情况.当p>1时，对差分解的影响不大，并且当计算过程长时间进行时，数值结果依然能保持稳定；当p<1，计算结果也没有发生明显变化，但是参数p取得过小，可能会使数值结果不稳定.