基于FTA方法的COVID-19疫情应急防控决策研究
李永勇, 张永进, 余珊珊
(安徽工业大学 数理科学与工程学院,安徽 马鞍山 243002)
0 引言
目前,COVID-19疫情在全球多点暴发,引起了国内外学者和相关研究人员的高度重视。基于相关部门公开的COVID-19疫情数据,研究人员主要通过模型仿真方法研究疫情防控措施,以及预测疫情发展态势。针对COVID-19的早期传播行为,李倩等[1]、范如国等[2]和周涛等[3]用SEIR动力学模型对COVID-19疫情发展进行了仿真分析和预测。基于COVID-19的传播机理、追踪隔离染病者的密切接触者、及治疗等干预措施,白宁等[4]建立了非自治的动力学模型,对湖北省疫情发展进行了仿真预测和评估。基于疫情防控进程数据,李冀鹏等[5]提出了一种定量化评估相关地区防控效果的近似方法,并对武汉流出人口前50城市防控成效进行了合理评估。
全球各国是命运共同体,加强疫情防控国际合作、共享应对疫情治理方案是缓解与约束疫情在世界范围内蔓延的基本决策[6~8]。由于当前缺乏可靠的决策支持工具和共享数据,决策变得更加困难。Sperrin M等[9]建议定期咨询实时的系统评价,以确定何时可用准确的COVID-19临床预测模型并制定相应决策,从而使医疗保健各个领域患者受益。基于COVID-19疫情数据,Mangiarotti等[10]建立了一般动态环境下灵敏度较高的定性模型,为疫情防控提供了辅助决策。由于有限决策数据和可能发生的突发事件演化,应急决策问题往往具有一定风险性和不确定性。考虑到应急设施的中断风险,王宁等[11]提出了基于应急案例的情景决策支持方法来合理配置资源,提高应急设施的可靠性和抵御中断风险的能力。近期Karnon[12]构建了决策树对COVID-19大流行的即时锁定与渐进式决策这两种方案进行了综合评估。
目前,对于COVID-19的传播过程主要是通过仿真方式进行分析,虽然能够可视化地展示病毒的动态传播途径,但不能有效给出病毒感染和传播的全部要素及其逻辑关系;而且在应对COVID-19大流行的实际突发事件中,大多数预测模型的有效性依赖于大量的参数,所以相应的决策分析方法很少考虑决策问题的动态性和风险性。因此,本文提出一种基于故障树分析(FTA)方法,分析COVID-19疫情应急防控中具有动态演变和多情景下风险决策问题。首先,通过分析COVID-19疫情演化条件和因素之间逻辑关系,构建COVID-19传播故障树模型,预估出突发情景下每个可行应急方案概率,再计算出各方案排序值,确定可行最优应急方案。最后,对参数进行了局部灵敏度分析。
1 问题描述
1.1 新型冠病毒疾病(COVID-19)
政府采取一系列有效应急防控方案后,目前COVID-19疫情得到了有效控制。从疫情背景来看,疫情防控是一个风险决策问题,且该疫情病毒传播具有多变动态特征,导致疫情防控方案会改变情景发生概率。因此,可通过分析可能影响突发疫情演变的条件和因素来估计情景发生的概率,据此找出理想疫情防控方案。
1.2 符号描述
基于突发的COVID-19疫情问题,给出相关决策的符号描述如下:
(1)考虑COVID-19突发疫情有m个可选择的应急方案,即M1,M2,…,Mm,标记应急方案集为M。
(2)对于上述可选的应急方案,其对应成本分别为c1,c2,…,cm,标记成本向量为C。
(3)COVID-19疫情在演变过程中存在n个潜在的情景,即D0,D1,…,Dn,标记情景向量为D,其中D0表示突发事件的当前的情景。任意a,b∈{0,1,…,n},如果b>a,则情景Db下损害结果比情景Da下损害结果更严重。
(4)评估COVID-19疫情的损害结果有k个判据,即N1,N2,…,Nk,标记判据集为N。
(5)情景Dj(j=0,1,…,n)在k个判据下的损害结果向量,用dj=(dj1,dj2,…,djk)表示,其中djl(l=1,2,…,k)为判据Nl和情景Dj下损害结果。
(6)COVID-19疫情下应急方案的成本权重标记为λc,0≤λc<1。
(7)上述k个损害结果判据对应权重分别为w1,w2,…,wk,标记判据权重向量为W,有λc+w1+w2+…+wk=1,其中,λc和W可通过德尔菲法(DM)[14]获得。
(8)在应急方案Mi下情景Dj发生的概率为pij,概率矩阵标记为P=[pij]m×n。
(9)在判据Nl下的COVID-19疫情应急方案Mi期望标准值表示为eil。
(10)根据构造情景的概率矩阵P计算不同应急方案Mi的整体排序值ei。

根据上述COVID-19疫情应急方案问题描述,估计概率矩阵P,并根据P选择最理想的应急方案,其应急响应中的风险决策树如图1所示。
在情景D0下的COVID-19疫情应急方案实施的结果有两种:一种是疫情突发事件以概率pm1演化为D1,另一种是以概率1-pm1结束。这里的pm1是在实施了应急方案Mm的情况下情景D1的概率,而不是在情景D0已经发生的情况下情景D1的条件概率。如果突发事件演变为情景D1,那事件要么以pm2的概率继续演变为情景D2,要么以pm1-pm2结束。以此类推,突发事件演变为情景Dn-1,也有两种可能的结果,即突发事件要么以概率pmn演化为情景Dn,要么以概率pm(n-1)-pmn结束。最后,如果情景Dn发生后突发事件结束,则损害结果向量为dn=(dn1,dn2,…,dnk)。
基于上述决策描述以及FTA方法,提出COVID-19的风险决策方法:首先,构造一个故障树来描述导致疫情演化的条件与因素之间的逻辑关系;再根据不同的应急方案计算不同情景的概率;最后,计算出各应急方案的排序值,并根据排序值确定应急方案的优先级。
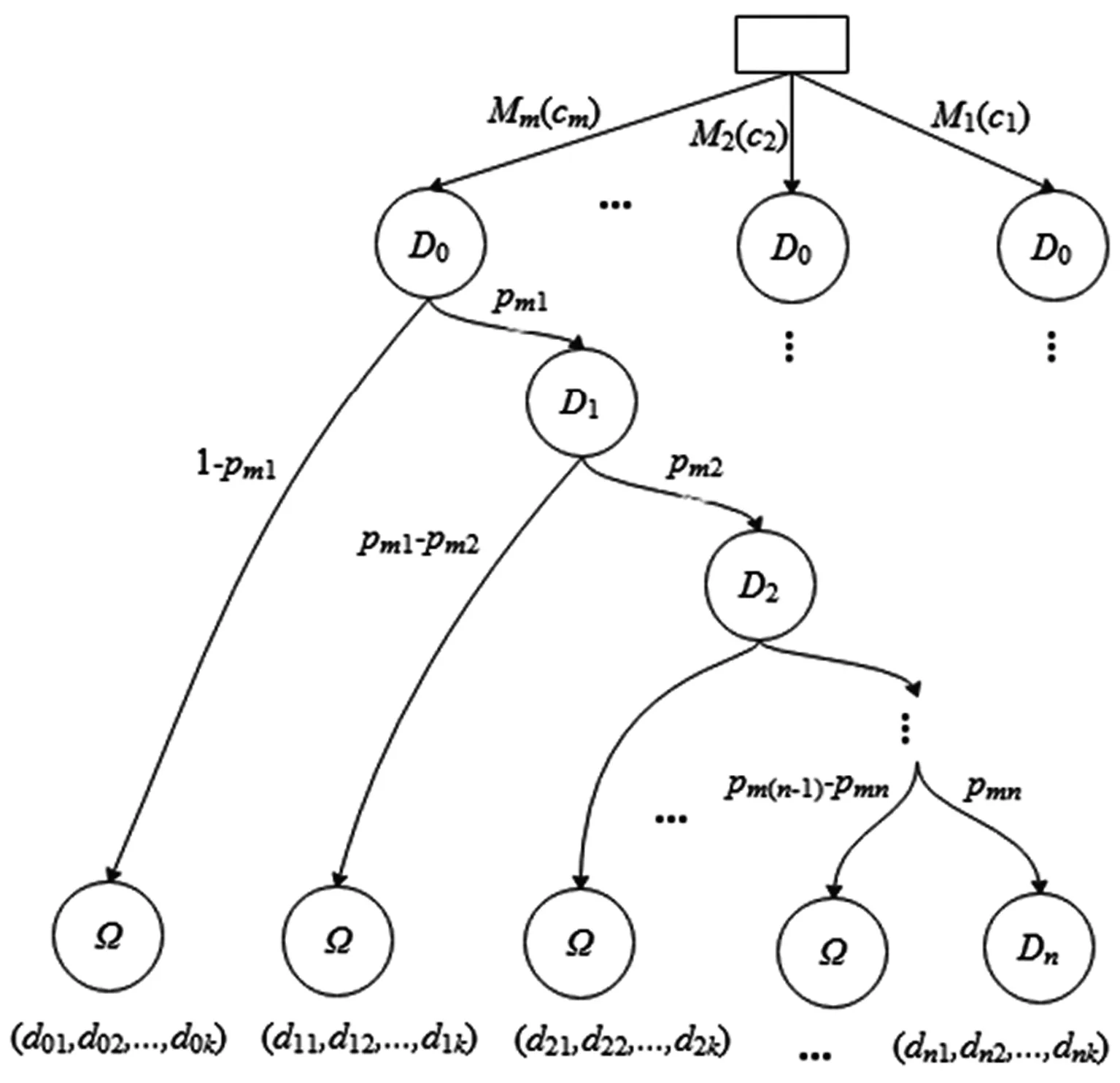
图1 COVID-19疫情响应的风险决策树
2 COVID-19疫情的FTA
FTA是一种分层演绎逻辑分析方法,可标明危及系统安全的故障发生具体底事件,并对其进行定性分析和定量分析,精确地找出故障原因。目前,FTA广泛应用于系统可靠性[15]、风险决策[16]等研究。COVID-19疫情传播故障树的构建是疫情在一定条件下逻辑推理过程,主要是识别疫情从最初情景演化为下一个情景条件和因素,逐层追踪分析并给出决策。过程如下:
步骤1选择和确定故障树的顶事件,该故障树顶事件为COVID-19疫情的传播。
步骤2定义COVID-19疫情边界条件。确立需要考虑哪些因素、状态、突发情况以及外部压力(如病毒变异);在细节上,还需确定多大程度上确定事件的潜在原因。
步骤3定义故障树中间事件和底事件。
步骤4确立故障树逻辑门。
根据上述步骤,构造出COVID-19疫情传播故障树,如图2所示。
3 应急方案的选择
3.1 情景概率的计算
根据COVID-19疫情传播故障树可写出情景的逻辑关系表达式,再估计底事件概率计算出不同应急方案下情景概率,过程如下:
首先,假设故障树存在q个事件X1,X2,…,Xq,记情景Dj的逻辑式为
ΨDj=Ψj(X1,X2,…,Xq),j=1,2,…,n
(1)
式中底事件和中间事件(顶事件)是通过逻辑运算符连接的,用逻辑运算符号“∪”表示“或”门连接;用逻辑运算符号“∩”表示“与”门连接。将应急方案Mi实施后的底事件Xh的概率表示为ρih,则Ψj(·)中的逻辑运算为Ψ(Xh∪Xh′)=ρih+ρih′-ρihρih′,Ψ(Xh∩Xh′)=ρihρih′,其中i=1,2,…,m,h=1,2,…,q。


(2)
其中,i=1,2,…,m,j=1,2,…,n,φj(·)是对应于Ψj(·)的函数。


图2 COVID-19疫情传播故障树
3.2 应急方案的排序
为了找出最理想的COVID-19疫情防控应急方案,根据构造的情景概率矩阵P计算不同应急方案的整体排序值,具体如下:
(a)标准化处理 为了保证结果的一致性,对成本和情景在相应判据下的损害结果进行标准化处理,则有
(3)
(4)


(5)
其中i=1,2,…,m,j=1,2,…,n-1。
(c)应急方案排序 根据λc和判据的权重值wl,计算COVID-19防控应急方案Mi的整体排序值e1,e2,…,em,确定所有可行的应急方案的排序,其中排序值ei为
(6)
其中i=1,2,…,m,l=1,2,…,k。ei越大,则优先选择应急方案Mi。
(7)
3.3 基于FTA的决策步骤
根据COVID-19疫情的FTA,以及应急方案的排序,应急防控决策步骤可归纳为
Step1构建COVID-19疫情传播故障树;
Step2根据Step1构建的故障树和式(1)确定情景逻辑表达式ΨDj;
Step3利用DM方法确定底事件概率矩阵Φ=(ρih)m×l;
Step4利用式(2)计算出在应急方案Mi下情景Dj发生的概率pij;
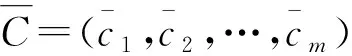
Step6利用式(5)计算期望标准值eil;
Step7利用式(6)计算排序值ei;
Step8将Step7得到的排序值e1,e2,…,em进行排序,并得出理想的应急方案。
4 案例分析
为验证所提出方法的可行性,下面以江苏某小区COVID-19疫情的应急防控为例。
2020年1月22日,一名现居江苏某小区的37岁男性患者被确诊,该病例为江苏省首例COVID-19确诊病例,引起当地相关部门的高度关注。该小区对疑似感染者进行隔离之外,在现有可行的应急方案中选出最优的方案来控制疫情的传播:
M1:仅对疑似感染者进行隔离。对疑似感染者进行隔离观察,可以防止病毒的持续传播,降低其他健康住户被传染的风险。M1的成本是0万元,即c1=0;
M2:对疑似感染者和密切接触者分别进行隔离和集中隔离。追查密切接触者病毒来源、活动轨迹、接触范围、隔离情况及检验结果,可有效阻断传播链,防止疫情进一步扩散。M2的成本是1万元,即c2=0.1。
M3:除了对所有密切接触者进行集中隔离,也对确诊感染者的楼层及电梯进行消毒处理,并每隔8小时收集一次相关楼层住户体温。对相应楼层及电梯消毒处理可降低住户乘坐电梯感染病毒的风险。观察体温变化,仍是发现感染者最简单直接的一种方式。M3的成本是1.5万元,即c3=0.15。
M4:除了对所有密切接触者进行集中隔离,还进一步管理小区住户,及时控制小区内的人口流动、对相应楼层进行消毒以及定时收集小区住户体温情况。对小区内住户流动的及时控制,能有效的降低住户感染病毒的风险。M4的成本是2万元,即c4=0.2。

M5:除了对所有密切接触者进行集中隔离,还及时对所有楼层进行消毒处理、控制住户流动以及定时收集小区住户体温情况。对所有楼层进行消毒以及控制住户流动,可有效防止病毒的进一步扩散。M5的成本是5万元,即c5=0.5。
M6:除了对所有密切接触者进行集中隔离,还对整个小区进行消毒处理、定时收集住户体温情况以及限制住户出入小区。对整个小区的消毒,严格把控住户的出入等措施,有效地降低疫情扩散风险,让疫情防控更加精准,最大限度保障住户安全。M6的成本是12万元,即c6=1.2。
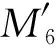
通过对该小区疫情进行分析,在疫情传播过程中,考虑以下四种可能情景:
D1:在密切接触者中发现新的感染者;
D2:在确诊患者及其密切接触者所在的楼层内发现新的感染者;
D3:小区内其他楼层发现了多名新的感染者;
D4:COVID-19在该小区内传播;
在做决策时,还需考虑下列判据:
N1:COVID-19在小区内感染程度;
N2:小区住户的恐慌程度;
N3:对小区声誉的负面影响。
判据N1、N2和N3值的范围在0到1之间 (恐慌或负面影响越大,对应的数值就越大)。不同情景下的判据值,如表1所示:

表1 不同情景下的判据值
该小区在疫情防控中,若坚持依法科学有序地防控,杜绝相关极端的防控措施,则由DM方法得出成本的权重λe=0.2和判据权重向量W=(0.4,0.2,0.2)。
4.1 选择最理想防疫应急方案
4.1.1 构建小区COVID-19传播的故障树
首先,确立顶事件为COVID-19在小区内传播D4。根据对以往类似传染疾病的分析,通过一个“与”门将COVID-19在小区内传播D4发生的可能情况分为“在小区其他楼层内出现了新的感染者D3”和“COVID-19的传染途径不确定E1”。
同样,可知导致其他楼层内出现新感染者D3发生的因素为“在确诊患者及其密切接触者所在楼层内出现新感染者D2”和“新增感染者与其他楼层住户接触X7”。两者通过“与”门连接,当同时发生时,才导致其他楼层内出现新感染者D3。COVID-19传染途径不确定E1可能是“通过空气、电梯等媒介物感染E2”或“通过其他未检测到的媒介物感染E3”,所以E2和E3是通过“或”门连接的。中间事件D2发生原因是在密切接触者中发现新感染者D1并且COVID-19具有潜伏性,使得感染途径监测失效E4;中间事件D1发生原因可能是密切接触者传染健康住户E5或家庭内有多人被感染X1,两者通过“或”门连接。通过一个“或”门分析COVID-19感染途径监测失效的可能原因,有确诊患者所在楼层没有及时消毒X4或新增感染者传染同一楼层健康住户E6。
最后,分别通过四个与门对中间事件E2、E3、E5和E6发生必要条件进行分析。通过空气、电梯等媒介物感染E2主要考虑了感染者进入其他楼层留下病毒X8和小区的其他楼层没有及时消毒X9这两个必须条件。小区内健康住户通过其他未检测到的媒介物感染E3的原因有其他楼层的感染者未及时发现X10以及在小区活动中与健康住户进行了具有传染性的接触X11。当确诊患者密切接触者已感染X2且未采取任何隔离措施X3,从而导致健康住户被感染E5。同理,新增感染者能够传染给同一楼层健康住户E6,主要是因为新感染人群未及时发现与隔离X5并在楼层内活动中与其他住户进行接触X6。由此构建出该小区疫情传播故障树,如图3所示。

图3 小区COVID-19传播的故障树
图3中故障树各底事件含义如表2所示。

表2 故障树中底事件的含义
4.1.2 计算不同应急方案下情景概率
根据图3可知,COVID-19在传播过程中存在情景的逻辑表达式为:
ΨD1=X1∪ΨE5=X1∪(X2∩X3)
(8)
ΨD2=ΨD1∩ΨE4=ΨD1∩(X4∪ΨE6)
(9)
ΨD3=ΨD2∩X7
(10)
ΨD4=ΨD3∩ΨE1=ΨD3∩(ΨE2∪ΨE3)
(11)
利用DM方法或间接启发式技术[17]判断故障树底事件概率的一致性,其底事件概率矩阵,如表3所示。

表3 底事件的概率矩阵
然后,根据式(2)、(8)~(11)可得在不同应急方案下构造情景概率,即
pi1=ρi1+ρi2ρi3-ρi1ρi2ρi3
(12)
pi2=pi1(ρi4+ρi5ρi6-ρi4ρi5ρi6)
(13)
pi3=pi2ρi7
(14)
pi4=pi3(ρi8ρiq+ρi10ρi11-ρi8ρi9ρi10ρi11)
(15)
最后,根据式(12)~(15)和表3可得出应急方案下各情景概率,如表4所示。

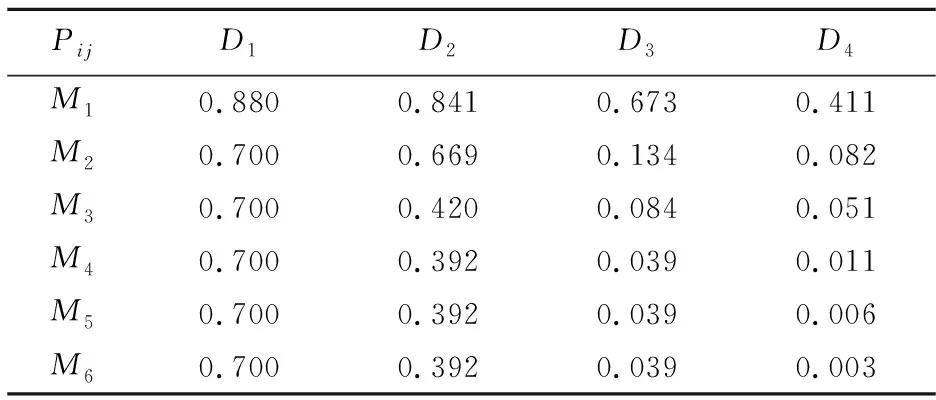
表4 应急方案下情景的概率
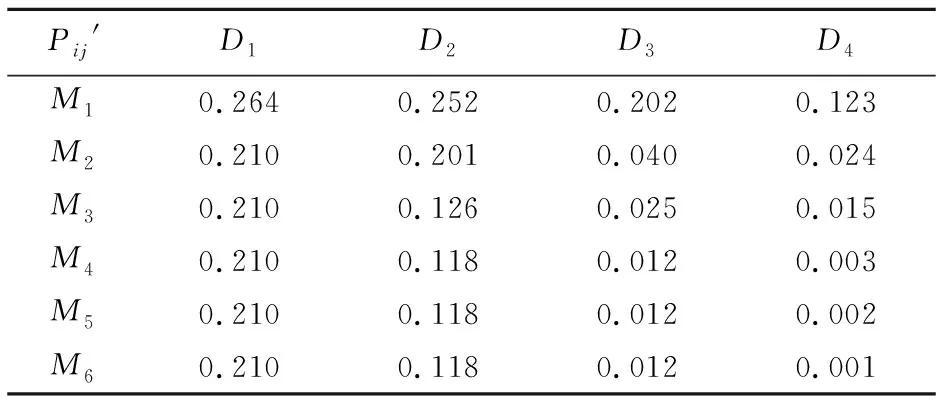
表5 极端情况下应急方案对应情景的概率
4.1.3 应急方案的排序
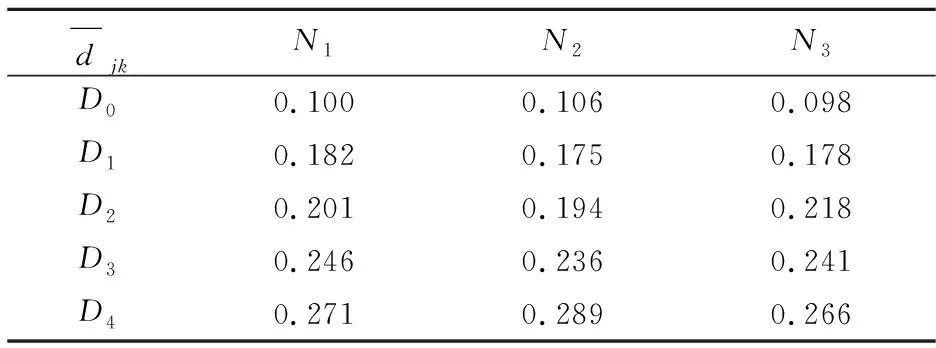
表6 归一化的标准值
然后利用式(5)确定不同方案的期望判据值eik,如表7所示。

表7 应急方案的期望判据值
利用式(6)计算出每个方案的排序值,即e1=0.7952,e2=0.8328,e3=0.8387,e4=0.8405,e5=0.8316,e6=0.7963。
当排序值ei越大时,对应的应急方案Mi就越好。
最后,根据应急方案排序值,确定可行应急方案的优先级,即M4>M3>M5>M2>M6>M1,因此在COVID-19疫情传播的防控中,该小区应优先采取经济有效地应急方案M4,以控制疫情在该小区的初步传播与发展。

表8 极端情况下应急方案的期望判据值
根据应急方案的排序值,确定可行应急方案的优先级,即M3>M4>M1>M2>M5>M6。
在极端情况下,该小区应优先采取应急方案M3,以便控制疫情初步传播与发展。
4.2 灵敏度分析
随着COVID-19疫情发展,应急方案选择会有所改变,需要分析局部参数变化对可行应急方案整体排序的影响。
4.2.1 底事件概率变化对方案排序的影响
对于突发事件,故障树底事件可分为两类,第一类是描述当前突发情景事件,其概率不会随着不同应急方案而改变;第二类是用来描述导致突发事件演变的条件和因素,其发生概率会随着不同应急方案而变化。下面对这两类事件分别进行敏感度分析。


4.2.2 成本权重变化对应急方案排序的影响

(16)


图7 在不同λc′下可行应急方案的整体排序值
根据λc′取值不同,可求出可行应急方案新排序值,这六种可行应急方案对应整体排序,如图7所示。如果λc′较小,则在应急方案M4、M5或M6选择最优方案;相反,如果λc′较大,则在应急方案M1、M2或M3中选择最优方案。
通过对疫情防控决策中局部参数灵敏度分析,可获得一些规律和启示。第一类底事件概率的变化会影响应急方案的整体排序。例如,在家庭内有多人被感染X1和密切接触者已感染底事件X2概率较大情况下,优先采取应急方案M4,即除了对所有密切接触者进行集中隔离,还进一步管理小区住户,及时控制小区内人口流动、对相应楼层进行消毒以及定时收集小区住户体温情况,反之采取应急方案M2。对于第二类底事件,虽然其概率变化不会影响最优应急方案排序结果,但是可以根据各底事件概率变化对应急方案整体排序敏感性进行预防,敏感性大的底事件重点预防,将会有效地减少COVID-19疫情突发事件的预期损害结果。
5 结论
根据当前疫情应急防控中风险决策问题,本文应用FTA方法对疫情防控进行了分析,主要工作与结论如下:
(1)用故障树描述了COVID-19疫情传播条件和因素之间的逻辑关系,并估算出有无极端情况下各可行应急方案的突发情景概率,然后计算出可行应急方案整体排序值,选择出理想应急方案;最后对决策方法中局部参数进行了灵敏度分析,为疫情防控决策提供了补充和支持。
(2)相比于已有决策分析方法,应用FTA方法不仅对疫情可能传播途径作了整体分析,还考虑其动态性、多情景风险及极端情景做法,而且可以在一系列可行应急方案中选择出最优应急方案,从而有效地控制疫情和降低应急方案成本。
(3)随着对COVID-19疫情认知不断丰富和完善,基于FTA方法的COVID-19疫情应急防控决策研究,为提升预防控制疫情等突发重大公共卫生事件的整体应急能力,以及快速识别防控薄弱环节提供思路和方法。

