基于改进NSGA-II算法的云制造服务组合优化研究

邵一凡, 禹春霞, 禹嘉诚

(1.中国石油大学 (北京)经济管理学院,北京 102249; 2.厦门大学 管理学院,福建 厦门 361005; 3.北京体育大学体育商学院,北京 100084)

0 引言

云制造的概念最早由李伯虎院士提出[1]，是一种面向服务的网络化制造新模式，其以客户为核心、以知识为支撑，构建了一个虚拟化、分布式、按需分配的资源共享平台[2]。在云制造模式下，分布式制造资源被封装到不同的云服务中，形成服务池，由云制造平台按需调配，极大地提高了制造资源的利用效率及社会生产力，为实现我国制造强国的目标提供了有力支撑。近年来，随着制造任务日益复杂，单一的云制造服务已无法满足生产需求，云制造平台需要将复杂制造任务分解为若干子任务，为各个子任务匹配合适的云服务，形成云服务组合，并在众多服务组合中选择最优组合供用户使用，这个过程称为云服务组合优化，是云制造平台亟需关注的问题。

在云制造平台中，针对同一个子任务有大量功能属性相同但非功能属性不同的云服务，云服务的非功能性属性通常用QoS(服务质量)来描述[3]。在实际应用中，云制造服务的QoS指标众多，因此云制造服务组合优化问题应被看作高维多目标优化问题。当前关于云服务组合优化问题的求解方式大致分为以下三种：第一种是将多目标问题转化为单目标问题进行求解[4～6]，第二种是直接利用多目标优化算法进行求解[7～9]，第三种是将所有组合枚举出来利用多属性评价方法选择最优组合[10]。在实际应用中，QoS指标间往往是相互冲突的，且转化为单目标优化问题进行求解时极容易陷入局部最优解，因此第一种方式可能会造成结果不准确，且非常依赖各指标权重；第三种方式在子任务及备选服务较多时会造成运算量呈指数型增长，不适用于大规模的云服务组合优化；第二种方式相对更加合理。但是当前采用第二种方式的多目标优化模型的目标函数的维度往往比较低，而云服务组合的评价指标众多，仅靠少数目标函数进行组合优化会相对片面。因此，本文提出的云制造服务组合优化问题的求解算法具有以下创新点：

(1)本文将云制造服务组合优化转化为高维多目标优化问题，从线上、线下两方面构建QoS评价体系。

(2)对多目标优化算法NSGA-II进行改进，提出一种基于nα支配的NSGA-II算法，使算法能够更好地处理高维多目标优化问题并消除量纲影响。

1 云制造服务组合优化模型

1.1 QoS评价指标体系

云制造服务包括线上交易与线下生产两部分，相对于普通制造服务来说，云制造服务需要更多地考虑网络性能以满足线上交易的需求；相对于基于web的云服务来说，云制造服务需要更侧重于线下生产制造的能力。因此，本文将云制造服务的评价体系分为线上和线下两部分，构建新的基于云制造的云服务QoS评价体系。

1.1.1 线上指标

云制造服务的线上部分要求其具备良好的网络服务性能，这一部分与web云服务非常相似，本文主要基于web云服务的QoS常用评价指标，从云制造的网络能力及线上服务能力两方面进行考虑，筛选出对云服务影响较大的四个指标：

(1)服务可用性(C1)：云服务在特定时间内能够被成功访问的可能性。

(2)服务安全性(C2)：云服务商为防止信息泄露，对用户数据传输进行保护及加密的能力。

(3)服务信誉度(C3)：用户在制造完成后对云服务商提供信息的准确性及制造过程诚信度的整体评价。

(4)信息共享能力(C4)：云服务商将其在平台中的制造及服务信息共享给其他共同协作服务商的准确性与及时性。

1.1.2 线下指标

云制造服务的线下制造部分要求其确保服务的价格及工期合理，且能够准确交货。对于复杂制造任务来说，需要各个服务间协同配合，因此物流运输能力对各个云服务也非常重要。本文选取的主要线下指标包括以下四个：

(1)价格(C5)：用户获取制造服务所需的成本，包括制造价格、服务价格等。

(2)交货准确性(C6)：包括云服务商交货的准时性、质量及数量等方面的准确性。

(3)工期(C7)：云服务商的交货时长。

(4)运输能力(C8)：云服务商在交货或运送到其他服务商时运输的安全性及准时性。

1.2 云制造服务组合模式与计算方式

如图1所示，云制造服务组合工作流程的基本模式包括四种：顺序、并行、选择和循环[11]，其中，CSSt表示第t个子任务的备选云服务集，θt表示选择执行第t个子任务的概率，k为循环结构的循环次数。对于云制造服务的四种执行结构，不同结构下的QoS属性值计算公式[12～14],如表A1所示。

图1 云服务组合结构

本文构建的云制造服务组合优化模型如下:

max[C1,C2,C3,C4,C6,C8]T

(1)

min[C,T]T

(2)

s.t.C≤Cmax

(3)

T≤Tmax

(4)

目标函数(1)表示云制造服务组合的服务可用性、服务安全性、服务信誉度、信息共享能力、交货准确性、运输能力6个指标尽可能达到最大化。考虑到相邻任务的各个云制造服务之间物流成本及时间，总成本(C)应包含制造的价格及物流成本，总时间(T)应包括制造工期及物流时间，目标函数(2)表示要使总成本及总时间尽可能最小。约束(3)和(4)表示云制造服务组合的总成本及总时间要低于用户提出的最大值限制。

2 云制造服务组合优化算法

2.1 nα支配

在目标函数维度较高时，基于帕累托支配的多目标进化算法会遇到收敛度显著下降的问题[15]。由于目标维度高，当一个个体A在极少维度下稍劣于另一个体B，但在其他维度上都明显优于B，此时理应认为A优于B，但按照帕累托支配的定义，这两个个体之间互不支配，这就很难找到一个个体支配另一个个体，导致帕累托前沿上的解集过大，使得算法的寻优能力大大降低。因此，在本文中将支配方式进行调整，利用α支配策略对个体进行分层。α支配的本质是在目标间进行折中，使得当个体x在某个维度上稍劣于个体y，但在其他维度上明显优于个体y时，允许x支配y。

以n个目标最小化为例，f1(x),f2(x),…,fn(x)为各个目标函数值，其中x∈X，X为优化问题的可行域。相对适应度定义为:

(5)

其中，x,y∈X。当∀i,hi(x,y)≤0，且∃i使hi(x,y)<0，则称x支配y[16,17]。当αij=0时为帕累托支配。

文献[17]利用DTLZ函数测试，验证了将标准α支配策略应用于NSGA-II算法的优越性能。但在实际问题中，需要考虑各个目标函数的计算方式及输入数据的量纲区别，利用标准α支配显然不合理，因此本文基于标准化思想，提出一种改进的α支配方法，记为nα支配，以去除量纲的影响且不影响最终输出结果。本文定义的相对适应度为:

(6)

其中，maxfi为第i个目标函数的最大值，minfi为第i个目标函数的最小值，以此来消除量纲，使得算法应用于实际问题时更为合理。

2.2 基于nα支配的NSGA-II算法

本文利用基于nα支配的NSGA-II算法对云服务组合优化问题的多目标优化模型进行求解，具体步骤如下：

Step1构建多目标优化模型，采用整数编码的方式，根据备选云服务的序号对各个云服务进行编码。

Step2初始化种群参数，设置种群规模、进化代数、交叉概率、变异概率及α的值，产生种群大小为N的初始父代种群Pt，t为种群代数，对所有个体进行基于nα支配的快速非支配排序及拥挤度计算。

Step3对父代种群Pt进行锦标赛选择。根据文献[18]的研究，在锦标赛选择策略中每次选择种群规模的60%～80%个体进行比较的效果最好，因此在本文中将每次比较的个体设置为种群规模的60%，选择非支配序小且拥挤度大的个体。由于本文的目的是求解一个组合优化实际问题，因此本文选用更加适合整数编码的均匀两点交叉[19]及邻近变异[20]产生子代，得到种群大小为N的子代种群Qt。

Step4将父代种群与子代种群进行合并。由于交叉及变异有一定概率，有些个体未进行交叉变异，且由于整数编码的特点，在交叉变异时可能会产生相同的个体，在多次实验中发现合并种群中重复个体较多，这严重影响种群了多样性。因此需要在种群合并后剔除重复的个体，若剔除重复个体后的种群规模小于N，则需要生成新的个体进行补位。

Step5对种群进行基于nα支配的快速非支配排序及拥挤度计算，筛选出种群大小为N的下一代父代种群Pt+1。

Step6判断是否达到进化代数的最大值，若达到则运行结束，输出非支配解集；否则令t=t+1，返回Step 3继续进行迭代直至达到进化代数的最大值。

3 云制造服务组合优选模型

在得到非支配解集后，需要从解集中挑选满足用户偏好的最优云制造服务组合。AHP法能够充分基于用户的偏好对权重进行合理分配，通过构建层次结构模型，获取用户两两比较判断矩阵，对指标重要程度按照1到9标度法进行比较赋值，最终求解出各指标权重。由于各个优化目标间不可相互补偿，为防止出现云制造服务组合由于某一目标下的值极好而将其他较差目标掩盖的情况，本文选取典型的非补偿算法ELECTRE对非支配解集进行优选。ELECTRE的原理是通过两两比较以获得决策集的二元关系，具有多种分支，不同类型的ELECTRE算法适用于解决不同类型的问题[21]。由于本文需要充分考虑用户的权重偏好对非支配解集中的服务组合进行排序择优，因此ELECTREIII算法更加适合本文问题的求解。

综上所述，本文通过AHP-ELECTRE III模型，基于用户对各个指标的偏好，对得到的非支配解集进行优选，具体步骤如下：

Step1基于评价指标体系C={C1,C2,…,Cn}，如表A2所示按照1～9标度法获得专家对各个指标重要程度的两两比较矩阵F=(fij)n×n,i=1,2,…,n;j=1,2,…,n。

Step2计算最大特征根λmax及特征向量W，并进行一致性检验。

Step3将解集标准化。

(7)

Step4计算可信度得分[22]。

由于传统的ELECTRE III的蒸馏过程具有复杂性，Wang[23]引入了一致可信度、非一致可信度和净可信度的概念，简化了方案的排序过程。

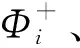
(8)

(9)

(10)

Step6根据Φi按照降序对方案做出排序，选出最优云服务组合方案。

4 实验与结果分析

4.1 算例描述

本节以一个电机制造任务为例，验证云制造服务组合优化模型的可行性。由于尚未有公开的数据集，本文采用在合理范围内随机生成的模拟数据验证模型的可行性和优越性。如图2所示，云制造平台将电机制造任务分解为六个子任务，构成子任务集STS={ST1,ST2,ST3,ST4,ST5,ST6}。同时企业要求总成本不超过850，总时间不超过90个单位时间。云制造平台为每个子任务匹配到7个符合制造要求的云服务，各个云服务的指标评价值及云服务间的物流成本、时间如表A3～表A8所示，其中子任务1不包括C8评价值。

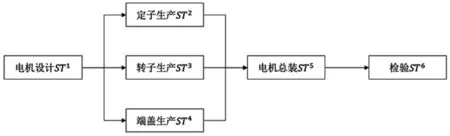
图2 电机制造工艺流程图

4.2 结果分析

4.2.1 可行性分析

根据整体任务结构及各个QoS值计算方式，算例构建多目标优化模型。子任务1与子任务2、3、4之间不涉及物流运输，其中，lc表示物流成本，例如lc35表示子任务3与子任务5相应云服务之间的物流成本，lc6end表示子任务6与用户之间的物流成本。lt表示物流时间，例如lt35示子任务3与子任务5相应云服务之间的物流时间，lt6end表示子任务6与用户之间的物流成本。

本文在Matlab 2017b环境中进行多目标优化模型求解，种群规模为150，进化代数200，交叉概率0.95，变异概率0.05，α=0.3，生成初始种群。按照2.2节所述步骤继续进行，直到输出非支配解集。输出的非支配解集及目标函数值如表1所示。其中服务组合中的数字表示对应子任务下备选云服务的编号，Ai为组合序号。

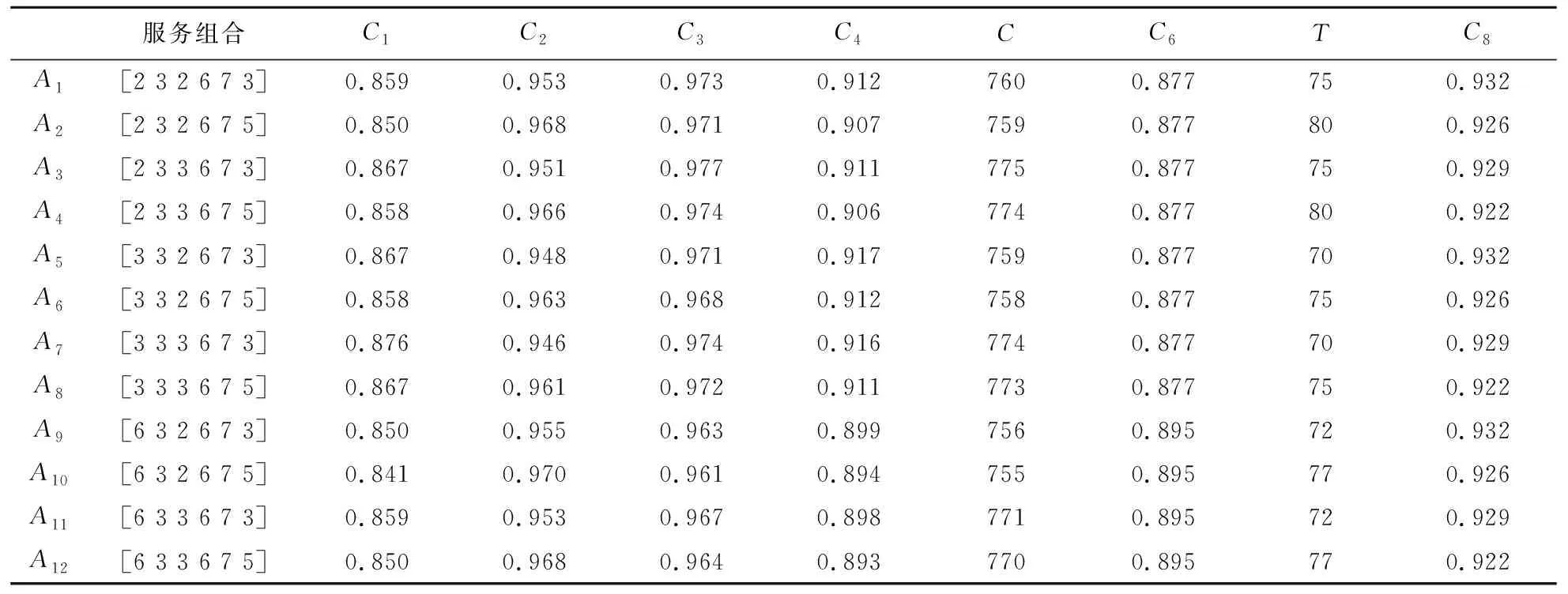
表1 非支配解集

基于得到的非支配解集，进行云服务组合优选，按照第3节所述流程，首先获得用户的两两比较矩阵，如表A9所示。

计算各个指标的权重并检验一致性，得到个指标权重如表2所示。一致性比率CR=0.0556<0.1，一致性检验通过。

表2 QoS指标权重

对非支配解集进行标准化，并取α=0.1，β=4，γ=0.6，计算出净可信度Φi，根据Φi按照降序对方案作出排序，结果如表3所示。

表3 备选云服务组合排序结果

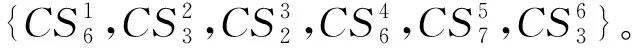
4.2.2 对比分析

为了验证本文提出的基于nα支配的NSGA-II优化算法在高维多目标优化情境下的优越性，本节对提出算法与标准NSGA-II算法、r-NSGA-II算法[24]和基于模糊支配的NSGA-II算法[25](以下简记为f-NSGA-II)进行对比实验。在Matlab 2017b中，分别设置种群规模(N)为50、100、150、200，进化代数200，交叉概率0.95，变异概率0.05。在nα-NSGA-II算法中，取α=0.3；在r-NSGA-II算法中，参考点取为各个目标可以达到的最优值，即(0.932，0.98，0.987，0.938，698，0.923，65，0.939)，各个目标权重均取0.125，阈值取0.3；在f-NSGA-II算法中，阈值取0.3。

由于进化算法每次输出结果有差异，因此本文在每个种群规模下采用四种算法分别独立进行10次实验，取非支配解集中各个优化目标的平均值，如表4所示，得到的平均最优解集的大小如图3所示。

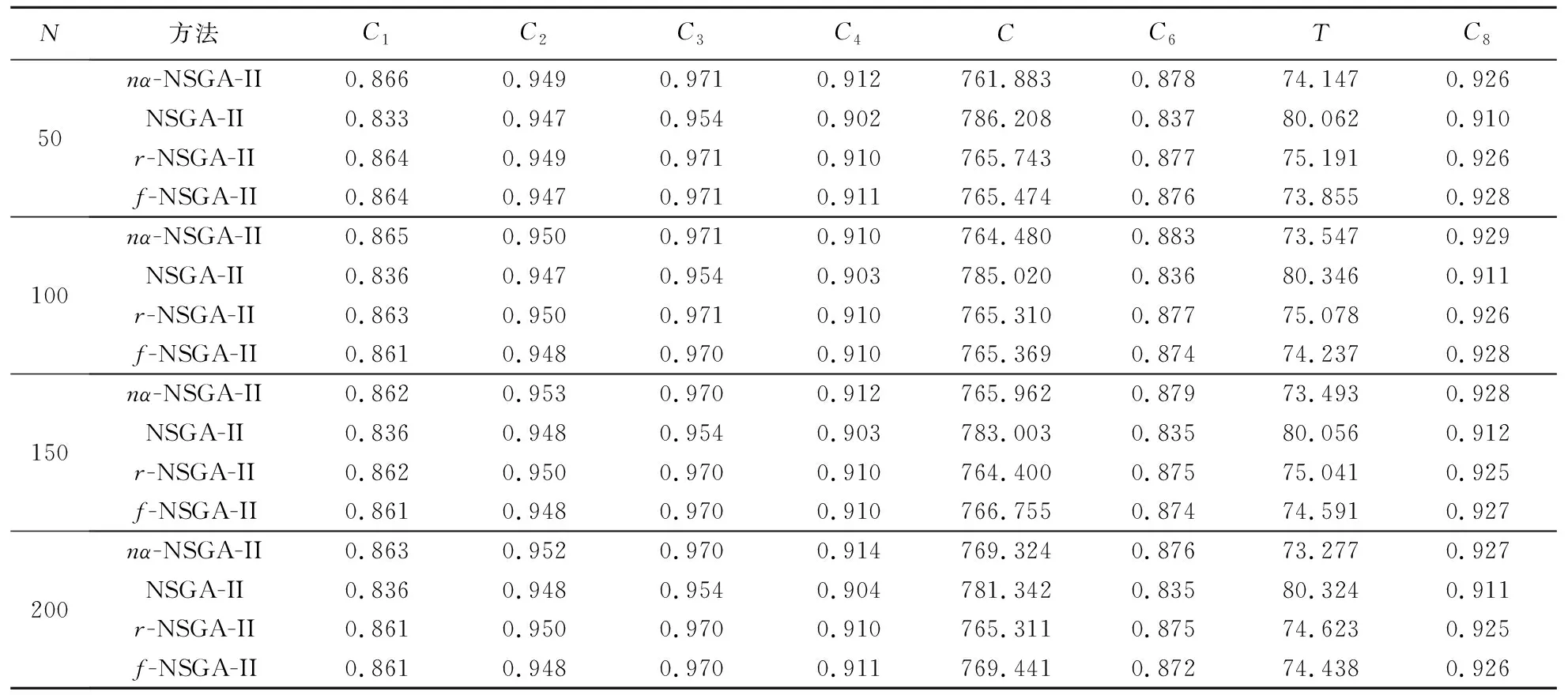
表4 不同种群规模下四种算法目标函数值对比

图3 四种算法最优解集个体数量对比

实验结果表明，基于nα支配的NSGA-II算法通过进化筛选出了整体更为优质的解集，在各个种群规模中，几乎所有目标函数平均值均优于或约等于其他算法。与其他算法相比，基于nα支配的NSGA-II算法非支配解集个体数目随种群规模扩大上涨不大，解集明显较小，大大减小了后续云服务组合优选的计算量。这是由于标准NSGA-II算法基于帕累托支配，在高维度情况下很难确定支配关系，从而导致解集占据了整个种群，进而使得各个目标下的平均函数值更差；r-NSGA-II算法非常依赖于参考点位置，解集收敛在参考点附近从而减小了种群多样性，在一定程度上影响了解集的目标函数值，随着迭代次数增加也使得解集中个体数量随之增加；f-NSGA-II算法的解集规模依赖于阈值的取值，阈值越大解集规模越小，但也会导致大量个体被分到最后一个层级无法区分；而基于nα支配的NSGA-II算法在高维多目标优化中能够根据α的取值在各个目标间折中，对种群进行更为有效分层，且不会向局部收敛，保证了种群多样性，得到更为优质的解集。

5 结论

云制造的发展使得云制造任务日趋复杂，进而要求从更多维度对服务组合进行筛选。本文针对云制造线上交易、线下制造的特点，构建了包含线上线下两部分的新评价指标体系。此外，本文基于新评价指标体系构建了高维多目标优化模型，并对多目标优化算法NSGA-II进行改进，提出了基于nα支配的NSGA-II算法。最后，本文通过一个电机制造的算例验证了本文提出模型的可行性，并通过与其他改进方法的对比实验证明了本文提出算法的优越性。

在实际生产中，可能会存在目标间相互关联的情况，因此需要进一步研究目标间相互关联时的多目标组合优化问题。同时，随着云制造平台的规模扩大，需要求解的组合规模及目标维度可能更大，因此在未来的研究中应考虑多种算法融合以提高算法性能。