道路维修施工路段交通分流信控优化模型
王 艳, 刘嘉晖, 陈 群
(1.湖南工商大学 公共管理与人文地理学院,湖南 长沙 410205; 2.中南大学 交通运输工程学院,湖南 长沙 410075)
0 引言
在道路维修施工期间,由于路段通行能力的大大降低,往往需要利用或开辟附近的辅路进行交通的分流组织,使得一部分车流经由辅路分流。对于道路施工期间交通组织研究,Vogel[1]讨论了安全指标“车头时距”和“碰撞时间(TTC)”。Hou等[2]针对三个不同的速度限制情景,对密苏里州农村的三个州际工作区进行了实地研究。Roy[3]从各种速度限制下降对碰撞频率和严重程度的影响出发,确定高速公路工作区的最佳速度限制。孟祥海等[4]分析了施工区上游过渡段车辆的排队特征。Wong等[5]使用单元传输模型(CTM)对具有两个紧密间隔工作区的双车道公路进行建模。Jacob等[6]利用机器学习,为受工作区影响的高速公路提供最佳的分流控制。Al-Kaisy等[7]对高速公路维修或重建施工区单线双向交通管制的有效性进行了评估。林泉[8]对厦门岛轨道施工期间的多层次交通组织对策进行了研究探讨。
针对在高速公路工作区域进行变速限制(VSL)控制的在线算法,Lin等[9]基于现场数据校准的模拟公路系统进行了广泛的实验。Radwan等[10]在存在VSL系统的情况下对动态车道合并(DLMS)系统的操作进行了有效性评估。Lee等[11]通过对比研究TOD、AFAR和ADAR信号控制方法,从双车道高速公路施工区的安全性和机动性的角度考虑,得到ADAR为大多数检查条件下最有效的控制方法。而且,可以利用可变信息标志(VMS)实现施工路段工作区的车道使用平衡,进而减少瓶颈处的事故率[12]。此外,针对高速公路高重复拥堵问题,Mazzenga等研究测试了主动交通管理系统对北弗吉尼亚州I-66和I-95施工区交通管理的有效性[13]。
上述的研究多分析了施工区域的速度控制、交通冲突、交通管理或指示与引导策略,而对辅路分流情况下的引导与控制优化缺少定量研究。本文将基于此,通过建立优化模型,对原路径和分流路径进行合理的交通量分配,以达到总的车辆延误时间最小化,为道路维修施工期间交通分流组织优化提供科学依据。
1 模型
1.1 问题分析与假设
道路施工期间,在所施工路段常采用部分车道封闭或半幅路面封闭,如图1。由于采用封闭部分车道或封闭半幅路面施工导致双向通行能力大大降低,此时一般需要进行交通分流。在车流上游路段通过开口引导部分车流从旁边的支路通行,如图1中的A→B的分流路径。本文下面只分析A→B的情况,B→A的情况可类似分析。
一般来说分流路径因为要绕行所以行驶距离较长,而且分流的路径通常要利用旁边的岔路和小道,所以分流的路径通行能力也是有限的。而原路径(路径1)如果通行的车流量小于因施工半幅路面封闭后折减通行能力,则经路径1会更快一些;而如果超出折减后通行能力(这经常会发生),则会引起排队,延误大大增加。因此,需要在交通分流路口安装信号控制灯,合理分配路径1和路径2的车流量,以使得车流总的通过时间最小。在本文讨论的道路施工路段交通分流信控优化中,有两个相位:一个是路径1显示绿灯,接着是路径2显示绿灯,中间有黄灯过渡,如图2。信控灯信号配时的主要参数包括信号周期、原路径上(路径1)绿灯分配时间及分流路径(路径2)上绿灯分配时间。在本文中不具体考虑黄灯时间,通常黄灯的前半段时间是可以通车的,可以算到绿灯时间内;而后半段不能通车的时间可算到红灯时间内。而且,信号配时是可以随上游车流到达率变化而动态调整的。
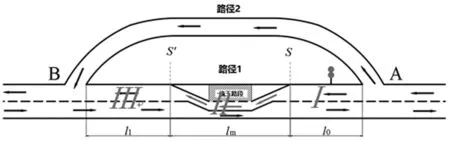
图1 半幅路面封闭施工形式交通组织
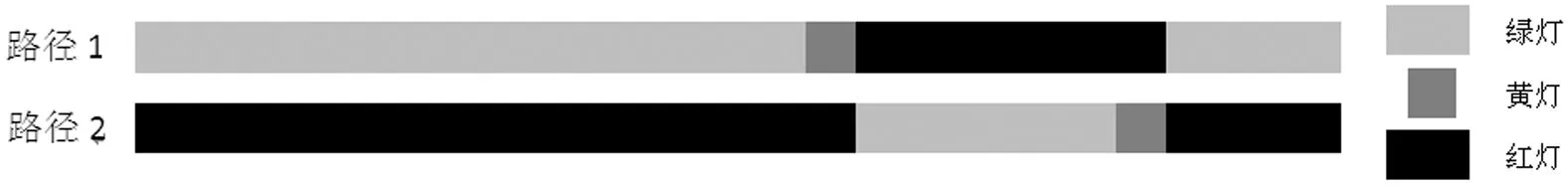
图2 道路施工路段交通分流信控优化相位
1.2 符合释义
1.3 模型建立
车流总行驶时间包括经路径1的所有车辆的行驶时间和经路径2的所有车辆的行驶时间之和以及信号转换期间带来的车辆延误,即:
T=T1+T2+T3
(1)
对于路径1,由于道路施工的影响(车道数变少,如图3(a)中在断面S处车道数由2变1),从区域Ⅰ到区域Ⅱ到达车流会在入口断面S发生拥挤。如图3(b)中所示,由于受区域Ⅱ车道数限制,进入区域Ⅱ的车流恒定为Qm,拥挤排队车流密度为kj。由于来车车流率Q0>Qm,会产生向后传播的集结波。根据车流波动理论[14],集结波波速见公式(2)。
(2)
在车流驶离施工区(区域Ⅱ到区域Ⅲ)时,车流是从高密度低速度向低密度高速度转变,车流会形成消散波。然而,由于区域Ⅲ通行能力大于区域Ⅱ通行能力,来自于区域Ⅱ的车流进入区域Ⅲ后车流率不变(即Q1=Qm),而车速会增加、密度会减小。在断面S′处消散波波速公式见公式(3)。
(3)
由式(3)知在断面S′处消散波波速为0,即在原地消散。
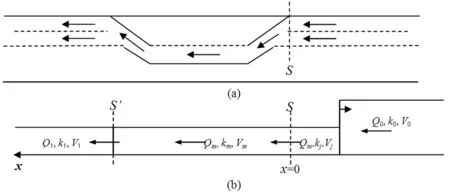
图3 车流运行过程及参数变化
如果信号灯对路径1显示为红灯时,则路径1到达车流量为0,此时在区域Ⅰ的拥挤排队车流将会逐渐消散。车辆运行时间-空间轨迹示意图如图4所示。
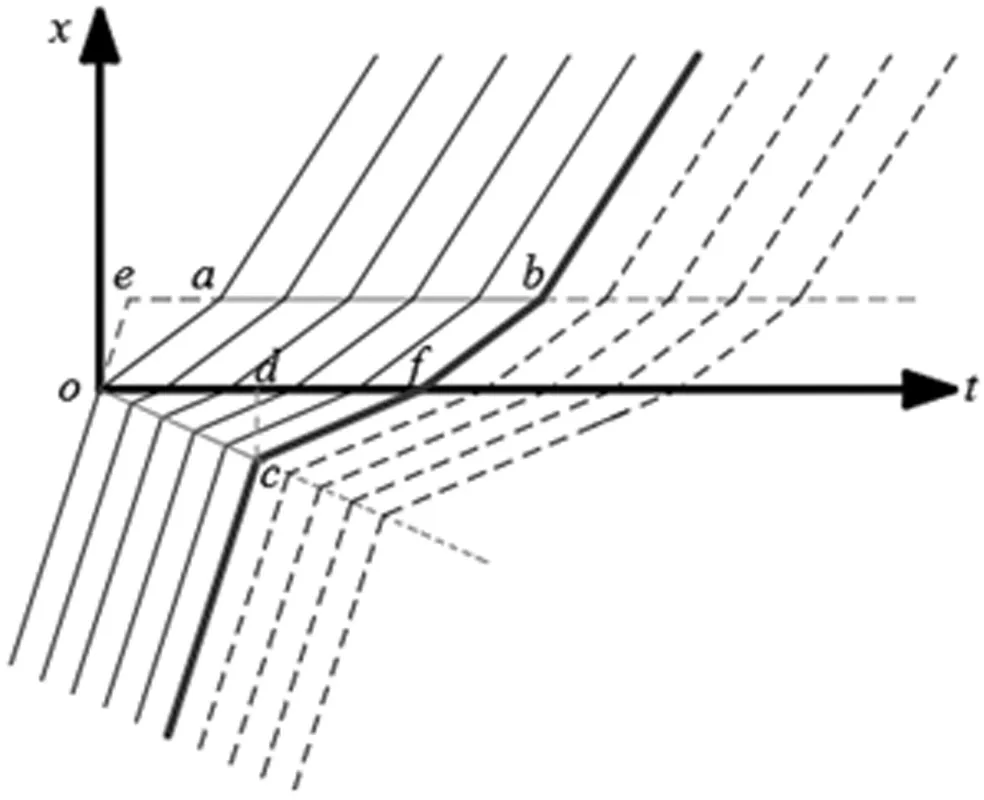
图4 车辆运行时间-空间轨迹
由图4可知,在断面S由于流入率大于流出率,车流形成集结波(波速为w1)。在a点对应的时刻(假设为ta),拥挤车流头车到达断面S′;车流密度由大变小使得车流在此处消散(如前所述消散波波速为零)。从车流排队处到断面S车流一直排队前进,前进速度为Vj;从断面S到断面S′车流前进速度为Vm。集结波波速为负,表示向车流反方向传播,即车流拥挤排队长度不断延长。为了达到良好有序的控制效果,车流拥挤排队长度不宜超过图1中A点(即路径1和路径2的交叉点),即需满足
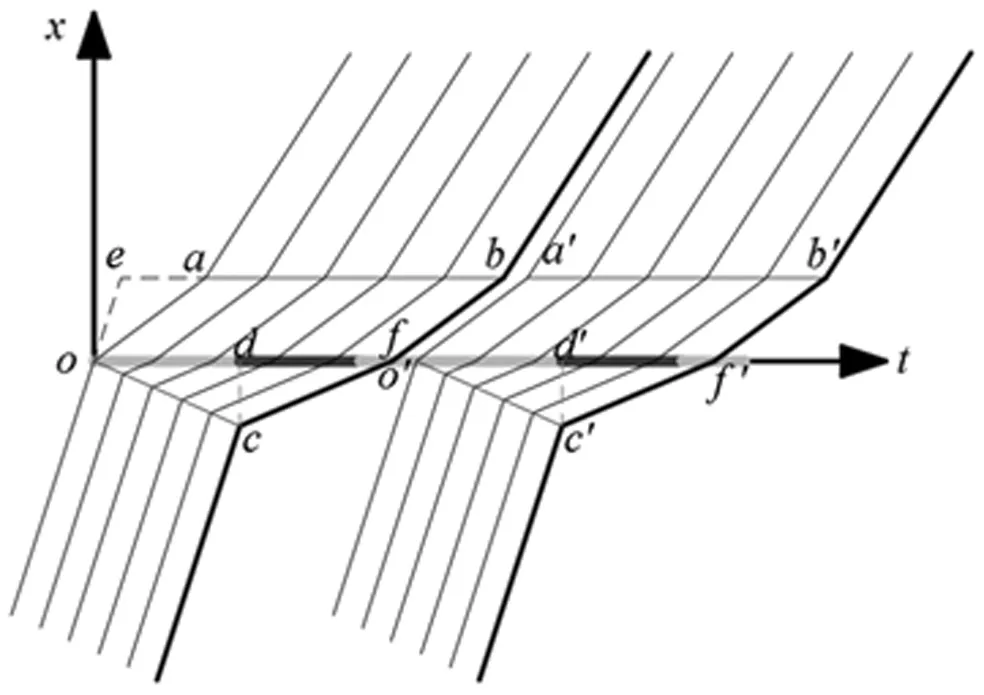
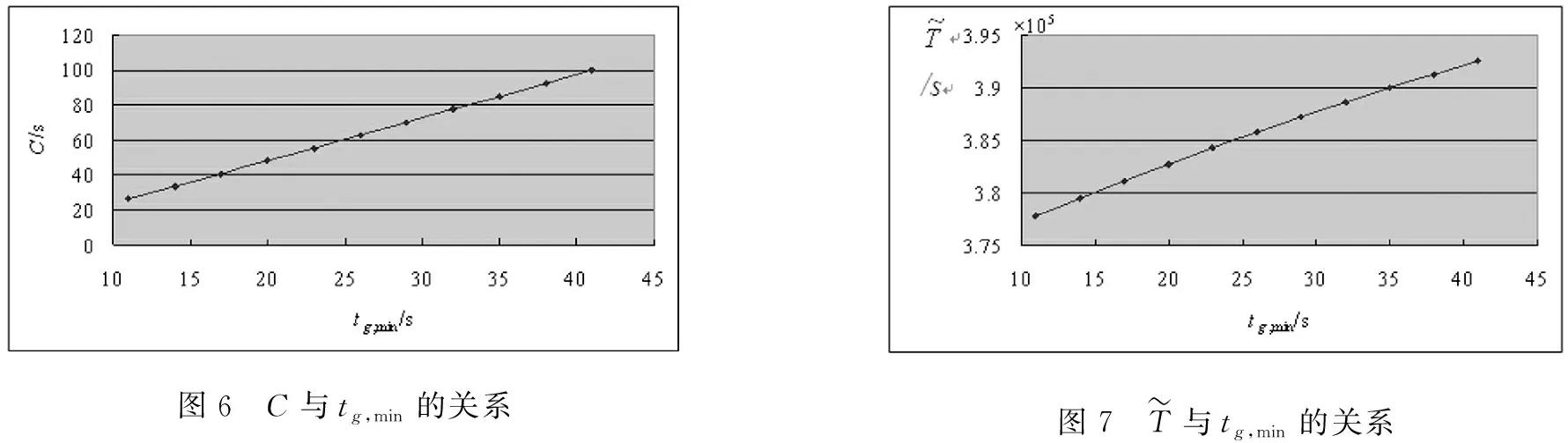
xc (4) 即为图4中c点所在位置,也即最大排队长度。在路口A点所设置的信号灯为限制驶入施工区所在路段的车流量。该信号灯针对由A到B的车流,绿灯亮起时要求驾驶员从路径1行驶,红灯亮起时(即路径2方向显示绿灯)要求驾驶员进入辅路从路径2绕行至B。图4中粗折线为信号灯为有效绿灯(包括黄灯的前半段)时的最后一辆通过交叉点A车辆的时空轨迹线。在一个信号周期C内,自ta(图4中d点所对应的时刻)时刻后,路径1禁止通行,车流进入辅道从路径2行驶。另外,为了确保在下个周期车辆到达S断面时不遇到上个周期余留的车辆(否则多个周期累积下来预留的车辆会越来越多,无法达到拥挤控制效果),在图5中O′点时上个周期的最后一辆车(即粗折线表示)应已离开断面S。 此外,某个周期对路径1车流开始绿灯时,头辆车在交叉点A到达断面S的行驶时间也是包含在(有效)绿灯时间内的。则信号配时关系如公式(5)、(6)。 (5) (6) 图5 路径1车流运行时间-空间轨迹 如图5,点f是一个周期中最后一辆车到达断面S的时刻。为了达到良好的拥挤控制效果(不造成前一周期的拥挤车辆的累积),下一周期头车到达断面S的时刻要在点f之后,即需满足 C>tf (7) 式(7)中tf为f点对应的时刻。由图5的关系可知 (8) (9) 其中,N1为一个周期内驶入路径1的车辆数,ta为车流在施工区(从断面S到断面S′)的行驶时间,te为假设在没有施工情况下(车速为V0)通过施工区的行驶时间,tb为一周期内最后一辆车从其排队位置c处驶离施工区的时间。 N1=Q0·tg (10) (11) (12) (13) (14) 则一个周期内经路径1从A到B的总车辆时间为 (15) (16) (17) (18) q<ρmax·e (19) 式(19)中ρmax为辅路上的最大饱和度,通常可取0.8左右。一个周期中总的损失时间为δ。假设对每个相位的损失时间(包括绿初启动损失和黄灯末损失时间)是相同的,则路径1和路径2的相位损失时间各为δ/2。上游到达的车流率为Q,绿灯显示下路径1中区域Ⅰ的到达车流率为Q0,绿灯显示下路径2分流的车流率Q2。因此,有下面式(20)、式(21)的关系。 (20) (21) 式(20)、式(21)表示上游来的车辆总是需要在有效绿灯时间内通过,且Q0>Q,Q2>Q。δ为一个周期中总的损失时间δ/2。每个相位的损失时间为Q·δ/2,则这个间隔时间排队等待的车约为δ/4。由于每个车道上排队长度较小,因此可将排队车辆按整体看待,平均等待时间为δ/4。因此,每个相位的总的停车等待时间为Q·δ/2·δ/4=Q·δ2/8,一个周期内总的停车等待时间为Q·δ2/4。 此外,每辆停车等待的车在停车线前面都需经历减速、加速的过程,假设每辆车减速和加速总的延误时间为ξ,则一个周期内所有需停车等待的车辆的总的加、减速延误时间为Q·δ·ξ,因此信号相位转换期间带来的车辆总延误为 (22) 由此,得到一个信号周期内的总的车辆行驶时间 (23) 将各相关参数代入,得到最终只包含优化变量tg、C的施工期间交通分流信控优化模型如式(24)~(30)。 (24) (30) (31) s.t.tg (32) y (33) y>W (34) (35) tg>tg,min (36) (37) 对于图1所示的分流网络,计算参数如下:α=0.15,β=4,l0=500m,lm=500m,l1=200m,ρmax=0.9,e=1400辆/h,q0=100辆/h。Q=0.5辆/s,Qm=0.3辆/s,V0=10m/s,V1=10m/s,Vm=6m/s,Vj=4m/s,kj=0.075辆/m,t0=200s。为了避免信号的频繁转换,Cmin=20s。δ=6s,ξ=5s。通过计算可得U=72,W=0.3556。不同tg,min下计算结果见表1。 表1 不同下优化结果 道路路段施工期间交通分流关系到交通通畅和施工的有序进行,本文建立了对道路交通利用辅路进行分流的信控优化模型。以车辆总的行驶时间最小为目标,并充分考虑了各种约束,建立了优化模型。并讨论了模型的解的性质,提出了一种近似求得最优解的办法。最后通过一个示例对模型和求解算法进行了验证,并对一些规律性结果进行了分析。本文的模型可用于实际道路路段施工期间的交通分流控制中,为工程实践提供科学依据。 本文主要还是限于理论模型探讨,模型中有关参数的取值以及最小周期约束等都需要今后结合具体工程实践进行论证。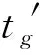

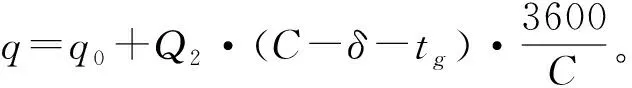

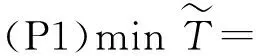
2 求解方法
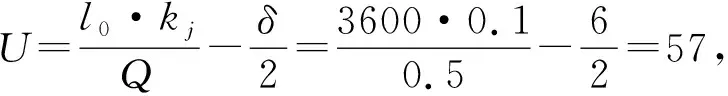
3 示例分析

4 结论

