含不相关机的动态可重入柔性流水车间问题的混合DABC-GA算法
轩 华, 刘淑燕, 王薛苑, 李 冰
(郑州大学 管理学院,河南 郑州 450001)
0 引言
柔性流水车间问题(flexible flowshop problem, FFP)是工业领域中较为常见的一类组合优化问题,它已被证明是NP-hard问题[1]。经典的FFP假设每个工件仅访问每个工序一次。然而,出于一些技术要求或质量考虑,有些工件需重新进入某些工序再次加工。这种特性导致了FFP的扩展,称之为可重入FFP,它广泛存在于许多实际生产系统,如半导体晶片制造、印刷电路板制造和薄膜晶体管液晶显示面板制造等[2,3]。考虑到制造企业设备更新替换需要昂贵的成本以及加工工艺的不同,假设工件动态到达生产系统的初端且阶段间工件运输不可忽略,本文研究了含不相关并行机和工件运输时间的动态可重入FFP(dynamic re-entrant flexible flowshop problem with unrelated parallel machines and job transportation time, DRFFP-UPM&JTT)。总加权完工时间问题已引起了众多学者的重视[3,4],它关系到在制品库存水平和准时交货等重要的物流指标,故本文以最小化总加权完工时间为目标解决DRFFP-UPM&JTT。
尽管RFFP-UPM相比经典FFP更为复杂,鉴于其强大的工业背景,已有不少学者对其展开了研究。为最小化makespan,Chamnanlor等[5]针对带时间窗约束和非等同并行机的RFFP,提出了混合蚁群优化的遗传算法(genetic algorithm, GA);Eskandari等[6]为求解含调整时间的DRFFP-UPM,提出了基于简单分派规则的启发式算法和基于变邻域搜索的元启发式算法。为最小化总拖期,Zhang等[7]提出启发式算法求解带非等同并行机的RFFP。针对RFFP-UPM的多目标问题,为最小化makespan和分时电价下的能耗成本,Geng等[8]提出了改进多目标蚁狮优化算法。
由于RFFP是NP-hard[3],难以用精确算法进行求解,故研究高效的智能优化算法具有重要的理论和实践价值。人工蜂群算法因其控制参数较少且性能具有竞争力,已成功用于求解车间调度。为最小化makespan,Li等[9]提出了离散人工蜂群(discrete artificial bee colony, DABC)算法求解带调整时间的分布式FFP;Li等[10]提出了DABC算法来求解含资源约束的FFP;Kheirandish等[11]提出了DABC算法和GA求解具有多级产品结构和非等同并行机的两阶段FFP;李俊青等[12]给出了混合DABC算法求解等同并行机或异构并行机FFP;为求解考虑搬运设备和有限缓冲区的单件车间调度,张维存等[13]设计了采用角色互换的改进ABC算法。针对多目标FFP,Peng等[14]为炼钢-精炼-连铸过程的FF再调度提出了改进ABC算法以优化效率目标和系统不稳定目标;Zhang等[15]研究了带可变加工速度的FF绿色调度,提出了基于分解的多目标DABC算法以最小化makespan和总能耗。
综上所述,在不相关并行机环境下的RFFP的研究多聚焦于makespan问题,而且很少探讨工件的动态特征以及工件运输与生产调度的协调问题。既有ABC算法多用于求解FFP,如何有效求解DRFFP还需进一步研究。基于此,本文研究了更贴合实际生产的含不相关并行机和工件运输时间的DRFFP,在DABC算法中嵌入遗传算法提出了一种混合DABC-GA算法以得到近优解。
1 DRFFP-UPM&JTT模型建立
1.1 问题描述
所研究的DRFFP-UPM&JTT描述如下。有I个工件经一条生产线的T个生产阶段上进行加工,工件以S1,S2,…,ST的顺序多次往复加工,每个工件i访问特定阶段Hi次,故每个工件共需Hi×T道工序完成加工。每个阶段t有Mt台不相关并行机,工件在阶段t加工时可指派到该阶段的任意一台并行机,其加工时间取决于处理该工件的机器。每个工件i在释放时间Ri到达生产系统,它在完成一道工序的加工后经运输送至下道工序的机器上,其运输时间由生产阶段间的距离来决定。机器在整个加工过程连续可用,每台机器一次至多处理一个工件,而每个工件一次至多选择一台机器加工。调度目的是在每个阶段将工件分配到机器且对指派到同一台机器的工件进行排序,目标是最小化总加权完工时间。
1.2 符号表示
定义参数与变量符号如下。
参数:
I:总工件数;
T:总阶段数;
ktm:阶段t上机器m加工的工件总数;
Mt:阶段t可利用的不相关并行机数;
Hi:工件i的总重入次数;
i,i′:工件,i,i′=1, 2, …,I;
t,t′:阶段,t,t′ =1, 2, …,T;
m:机器,m=1, 2, …,Mt;
gi:工件i所处的加工层;
rtm:阶段t上分派到机器m加工的工件集内第r个工件,rtm=1,2,3,…,ktm;
Ri:工件i到达初始生产阶段的时间;
Wi:工件i的权重;
Vgi,t-1,t:工件i在相邻两阶段间的运输时间,Vgi,0,1表示由第gi-1层的最后一个阶段T运送至第gi层的第一个阶段的运输时间,当gi>1时,Vgi,0,1>0,否则,Vgi,0,1=0;
Pitgim:工件i在第gi层的第t阶段的机器m上的加工时间。
决策变量:
Bitgim:工件i在第gi层的第t阶段的机器m上的开工时间;
Citgim:工件i在第gi层的第t阶段的机器m上的完工时间;
LCitgi:工件i在第gi层的第t阶段的完工时间;
Zitgim:若工件i在第gi层的第t阶段的机器m上进行加工,Zitgim=1,否则,Zitgim=0。
1.3 模型构建
利用上述符号,将DRFFP-UPM&JTT建模如下:
(1)
(11)
目标(1)是最小化总加权完工时间;约束(2)表示每个工件在任一阶段只能分派到一台机器;约束(3)表示在并行机上加工的工件总数为所有工件重复进入生产系统的总次数;约束(4)说明了分派到同一台机器加工的相邻两工件的加工优先级关系;约束(5)表示同一层内工件的前道工序完成后运送至下一阶段才能开始下道工序的加工;约束(6)描述了同一工件在上一层的最后阶段与下一层第一个阶段的工序加工优先级关系;约束(7)为加工时间要求;约束(8)定义了工件完工时间;约束(9)描述了工件开工时间不得早于其释放时间;约束(10)和(11)定义了变量取值范围。
2 混合DABC-GA算法
基本ABC算法从随机产生的蜜源开始,连续执行三个阶段(雇佣蜂、跟随蜂和侦察蜂)的搜索,直到满足给定的终止条件,它主要用于解决连续型问题,而本文所研究的DRFFP-UPM&JTT为离散组合优化问题,故提出了混合DABC-GA算法进行求解,在DABC算法中引入GA改善跟随蜂的搜索效率。首先,设定迭代数Maxcycle和与被放弃蜜源相关的限定搜索次数Limit,定义蜜源a∈{1,…,N},设计调度解的编码和解码方案,初始化种群A={X1,…,XN};然后,依次执行雇佣蜂、跟随蜂和侦察蜂阶段。
2.1 编码和解码
2.1.1 编码方案
基于上述模型设计了基于批量工件的元胞矩阵编码方案,基于不相关并行机机器号对工件在整个调度范围内的加工机器流进行表述,矩阵内的每个元素(即机器号umitg)服从[1,Mt]均匀分布,蜜源为由I个矩阵组成的元胞数组,它对应工件的调度。

图1 实例的编码表述
图1为I=2、T=2、Hi=2、M1=3且M2=2的一个实例编码,其中,每列表示在层gi工件i在各阶段加工时选择的机器号;每行表示在阶段t工件的各层工序的机器分配;虚线框内矩阵在蜜源中所处位置即为随机生成的工件加工序列β。
2.1.2 解码过程
通过解码将上述解表示为可行调度表。按照加工序列β依次安排各个工件的加工。对于阶段1,在第一层,将工件i分配至各自释放时间之后可利用的机器m(m=umi11)上;在重入层gi(gi≥2),计算工件i到达该阶段的时间Ci,T,gi-1,m+Vgi,0,1,记录工件i在该阶段同一台机器加工的紧前工件i′的完工时间Ci′1gi′m,则工件i在重入层gi的第一阶段的机器m(m=umi1gi)上的开工时间Bitgim=max(Ci,T,gi-1,m+Vgi,0,1,Ci′1gi′m)。对于其它阶段t,比较工件i到达该阶段的时间Ci,t-1,gi,m+Vgi,t-1,t与工件i在该阶段同一台机器加工的紧前工件i′的完工时间Ci′tgi′m,取max(Ci,t-1,gi,m+Vgi,t-1,t,Ci′tgi′m)作为工件i在重入层gi阶段t的机器m(m=umitgi)上的开工时间。
下面以图1为例详细说明上述解码过程,其中工件释放时间Ri、权重Wi、加工时间Pitgim以及运输时间Vgi,t-1,t见表1。由图1可知,工件加工序列为β={1,2},工件的机器分配方案及完工时间计算如下:

表1 实例数据
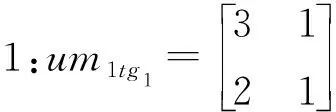
Z1111=Z1112=Z1211=Z1213=Z1122
=Z1123=Z1222=Z1223=0
Z1113=Z1212=Z1121=Z1221=1
B1113=R1=5
C1113=B1113+∑mP111mZ111m=5+9=14
B1212=C1113+V112=14+3=17
C1212=B1212+∑mP121mZ121m=17+10=27
B1121=C1212+V201=27+1=28
C1121=B1121+∑mP112mZ112m=28+5=33
B1221=C1121+v212=33+3=36
C1221=B1221+∑mP122mZ122m=36+5=41
W1LC122=7×41=287

Z2111=Z2113=Z2211=Z2213=Z2121
=Z2122=Z2222=Z2223=0
Z2112=Z2212=Z2123=Z2221=1
B2112=R2=3
C2112=B2112+∑mP211mZ211m=3+7=10
B2212=max{C2112+V112,C1212}=max{10+3,27}=27
C2212=B2212+∑mP221mZ221m=27+9=36
B2123=max{C2212+V201,C1113}=max{36+1,14}=37
C2123=B2123+∑mP212mZ212m=37+6=43
B2221=max{C2123+V212,C1221}=max{43+3,41}=46
C2221=B2221+∑mP222mZ222m=46+10=56
W2LC222=10×56=560
minO=∑iWiLCi22=287+560=847
据此可得到如图2的调度时间表,图中矩形框内(i,gi)对应处于加工层gi的工件i。

图2 实例调度甘特图
2.2 初始种群

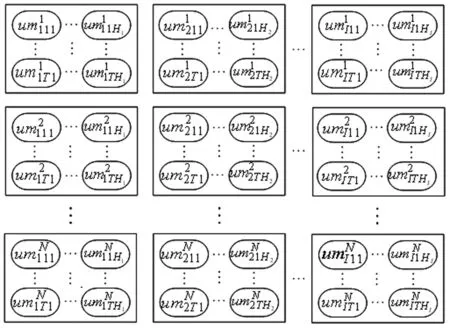
图3 初始种群
2.3 雇佣蜂阶段
在雇佣蜂阶段,在蜜源Xa附近采用高斯变异进行搜索。设计一种由当前最佳解引导的高斯变异搜索策略,基于Xa添加一个服从高斯分布的随机扰动项,借助该扰动项进行邻域搜索。因此,新蜜源Xnew产生如下:
Xnew=Xa·(1+N(0,1))
(12)
上式中,N(0,1)为满足正态分布、期望值为0且标准差为1的随机数。
2.4 跟随蜂阶段
在跟随蜂阶段,对雇佣蜂反馈的蜜源采用GA进行搜索以获得较好的邻域解。
2.4.1 适应度评估和选择
用于混合DABC-GA算法的评估函数定义为总加权完工时间的倒数,即第a个蜜源的适应度函数表示为式(13)。采用轮盘赌规则进行选择,目标值越优则它被选择的概率越大。
(13)
2.4.2 自适应交叉和变异算子
设计自适应交叉和变异概率Pc、Pm,使其随迭代数及适应度值而变化。令σ和τ表示权重因子;定义fmax和favg分别为种群A的最大适应度值和平均适应度值;令h为当前迭代数,Pcmax和Pcmin、Pmmax和Pmmin分别为交叉概率和变异概率的上下界。
当交叉蜜源中较大的适应度值f′高于favg时,Pc计算如下:
Pc=Pcmax-(Pcmax-Pcmin)×
(14)
否则,Pc=Pcmax。
当变异蜜源适应度值f高于favg时,Pm计算如下:
Pm=Pmmax-(Pmmax-Pmmin)×
(15)
否则,Pm=Pmmax。
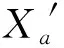

图4 基于工件加工序列的交叉算子
变异算子采用基于工件加工机器流的单点变异方式,在A中随机选择某个蜜源中一个变异位λ∈(1,I),重新生成第λ个位置的工件加工机器流,使其转化为近似解再进行择优,如图5所示。

图5 基于工件加工机器流的单点变异算子
2.5 侦察蜂阶段
3 实验设计与分析
3.1 实验设计
为验证算法的有效性,将混合DABC-GA算法和传统GA、嵌入变邻域搜索的GA(VNS-GA)以及文献[3]提出的结合NEH启发式算法的改进GA(NEH-IGA)做对比。所有算法采用Matlab R2014a编程,在CPU为Inter Core i5-5200U CPU 2.20GHz,内存为4.00GB的微机上运行。
测试实例由参数{I,T,Hi,Mt}的不同组合构成,其中I={30,50,70,90,120},T={3,5},Hi={2,3},Mt={5,6,7},共产生5×2×2×3=60种不同问题规模,每种规模运行10次。Pitgim∈U[5,10],Wi∈U[5,10],Ri∈U[1,5],Vgi,t-1,t∈U[1,5]。为了公平比较上述四种算法,经大量实验测试,设置GA、NEH-IGA、VNS-GA和DABC-GA的种群规模N=80,Limit=5。以DABC-GA运行60次迭代所需的时间作为所有算法的停止条件。定义相对偏差率RDI为:
RDI=(Oξ-Obest)/Obest*100%
(16)
其中,Oξ表示由算法ξ(ξ∈{GA,NEH-IGA, VNS-GA, DABC-GA})获得的目标值,Obest为由所有算法得到的最佳目标值。
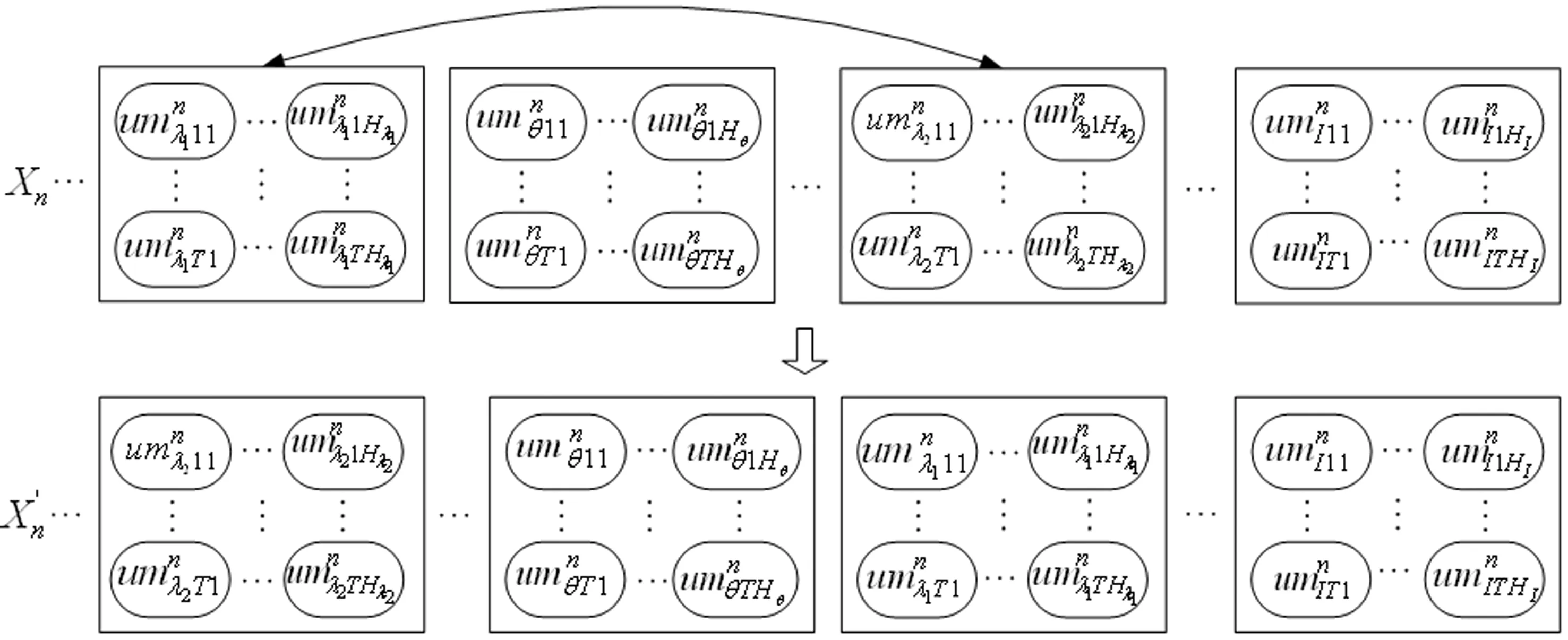
图6 基于工件加工序列的反转操作
3.2 实验结果及分析
不同规模测试结果见表2和表3。表中,列ARDI表示平均RDI值,列CPU和minO均为同一组实例的十次测试结果的平均值。

表2 中小规模问题的测试结果
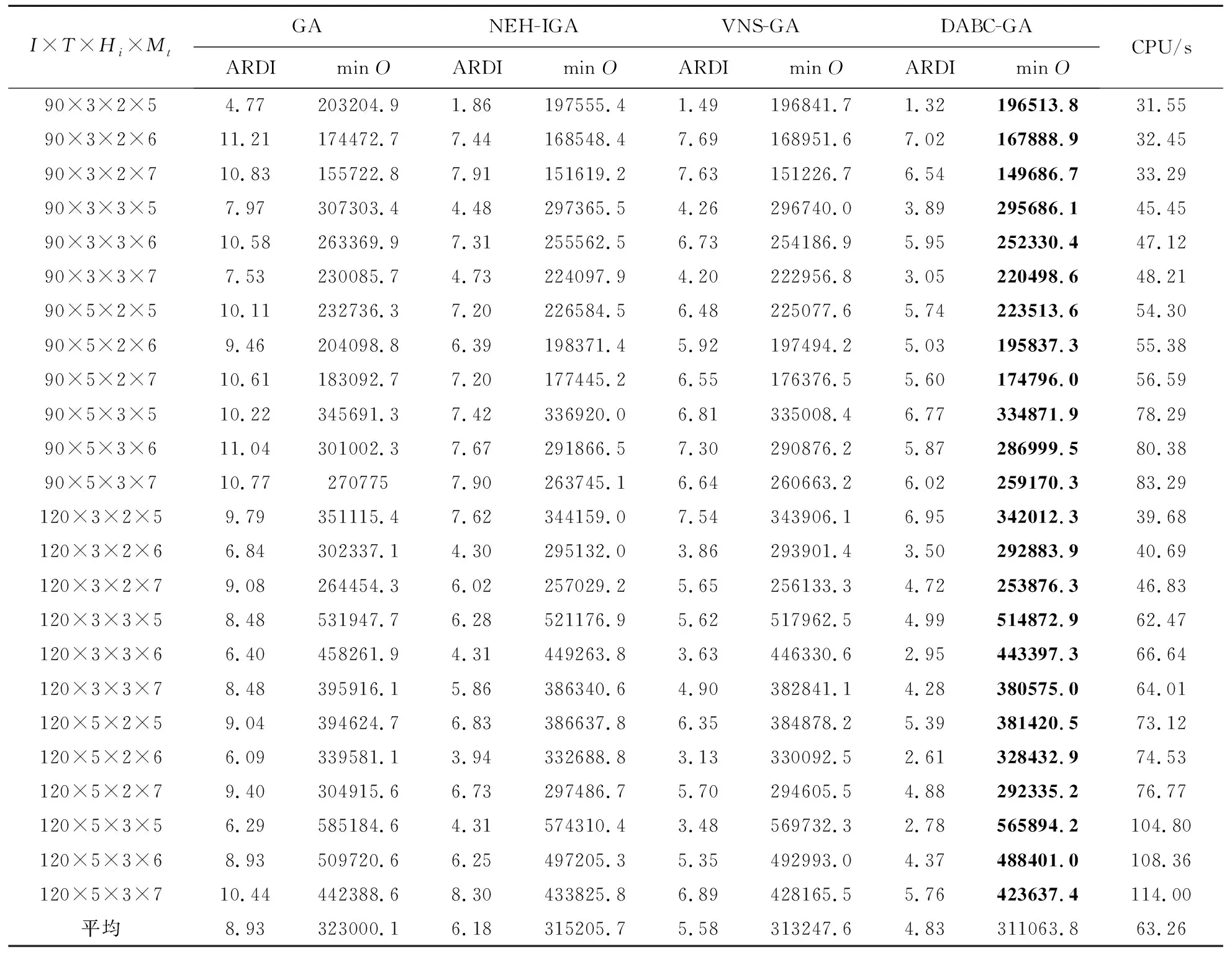
表3 大规模问题的测试结果
由表2和表3可看出,对于中小规模和大规模问题,由GA、NEH-IGA、VNS-GA、DABC-GA得到的ARDI分别为12.62和8.93、8.03和6.18、7.70和5.58、6.92和4.83;得到的平均目标值分别为90218.7和323000.1、86971.4和315205.7、86585.7和313247.6、85954.4和311063.8。因此,对于所有规模问题,在相同运行时间内,由DABC-GA得到的ARDI值和平均目标值均低于其它三种算法。
从总体性能来看,在平均CPU时间为49.5s内,由GA、NEH-IGA、VNS-GA、DABC-GA得到的ARDI分别为10.775、7.105、6.64、5.875;平均目标值分为206609.4、201088.55、199916.65、198509.1,这也说明DABC-GA获得了更好的近优解。
4 结论
本文研究了每阶段含不相关并行机的动态可重入柔性流水车间问题,以最小化总加权完工时间为目标构建了整数规划模型,进而,提出一种混合DABC-GA算法进行求解。根据DRFFP-UPM&JTT的特性,设计了基于批量工件的元胞矩阵编码,采用高斯变异使雇佣蜂进行有效的邻域搜索,在跟随蜂阶段引入GA进一步扩大解空间,针对侦察蜂设计了基于当前最佳解的反转操作,大量的仿真测试验证了所提出的混合算法的有效性。未来研究可继续探讨其它单目标或多目标问题;或者引入调度过程的其它动态特性,以扩展所提算法的应用;还可研究其它元启发式算法求解DRFFP-UPM&JTT的能力。

