带有机器维修和两车辆派送的单机排序问题
蔡 伟, 杨 梅
(1.南京审计大学金审学院 基础教学部,江苏 南京 210046; 2.中国石油大学(北京)克拉玛依校区文理学院,新疆克拉玛依 834000)
0 引言
件加工及派送和机器带维修区间的排序问题是两类重要的排序问题,由于这两类排序问题在工业生产与物流管理中应用前景广阔,所以近年来得到了广泛关注,而将两者相结合的排序问题,与实际的生产生活结合更加紧密,具有更为重要的应用价值。
对于加工及派送的排序问题已有大量学者进行了研究,如:Maggu等[1]首次考虑了工件需要运输的问题,研究了两机器流水作业问题,工件在第一台机器上加工完成后由有限数量的运输工运送到下一台机器上继续加工,每个工件的运输时间由该工件决定,并利用Johnson算法解决了该问题。Chang等[2]考虑了目标函数是极小化最大工件完工时间的三类机器加工及运输问题,首先对于单机加工后由单车辆派送给单客户情形,他们证明了该问题是强NP-难的,给出界为5/3的近似算法,并证明了该界是紧界;其次对于两台平行机加工后由单车辆派送给单客户情形,他们证明该问题是强NP-难的,并提出界是2的启发式算法,并证明是紧界;最后对于单机器加工后由单车辆派送给两个客户情形,他们证明了该问题也是强NP-难的,并给出界为2的启发式算法。Li等[3]研究了工件运输到多个顾客的情形,给出了客户数固定的情况下,目标函数是极小化最大工件完工时间的多项式时间算法,对于单客户的特殊情形提出了时间复杂度较低的改进算法。Zhong等[4]对文献[3]所研究的单机单客户问题给出了界为3/2+ε的改进算法;对于平行机单客户问题提出了界是5/3的改进算法。Lu等[5]对文献[2]所研究的单机单客户问题提出了界为3/2的启发式算法;对于多客户情形,批次派送时间定义为该批次内工件最大派送时间的排序问题,提出了界为2的启发式算法,并证明了界为紧界。Dong等[6]研究了单机加工并由单车辆派送到多客户的排序问题,提出了界为2的启发式算法,并对客户数目为两个的特殊情况提出了界为5/3的启发式算法,并说明该算法是渐进紧的。Jiang等[7]研究了单机器分批加工并由两台同类车派送到单顾客的排序问题,提出了界为2的近似算法,并证明了该界是紧界。
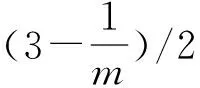
现有文献表明目前国内外研究仅考虑了机器维修和工件派送两者之一,很少将二者相结合;其次是只考虑到单车辆派送和工件体积相同等特殊的情况。这些较为特殊的情况都与实际生产生活中的企业、工厂的产业链及供应链有所区别。本文综合考虑机器维修和工件派送两类排序问题,对单机器加工后由两车辆派送到单客户的情形给出了近似算法,为企业的生产与供应链管理提供了理论依据。
1 问题描述及说明
本文研究的带有机器维修和两车辆派送到单顾客的排序问题,具体描述如下:给定工件集J={J1,J2,…,Jn},工件的Ji体积为si(0 h(1)机器具有一个维修区间D工件加工完成后需要派送 k顾客的数量,v同类车的数量 c同类车的容积,T工件派送所需时间 Δ维修时长,δ维修前空闲时间 P所有工件加工时间和 SPT序按加工时间不减排序,LPT序按加工时间不增排序 定理1问题1,h(1)→D,k=1|v=2,c=1,T|Cmax是NP-难的。 证明把工件的加工时间都看成0,此时与机器加工无关,只需将工件分批派送,即转化为一个装箱问题,由于装箱问题是NP-难的,则本文研究的问题也是NP-难的。 本文需要综合考虑工件加工与派送,那么算法整体可以构造为两阶段流水作业模型,然后利用已知算法求解;其次,用于派送车辆的车辆容积固定,加工之前可以按照车辆容积对工件分批再按照批次加工,加工完成的批次可以直接派送;最后,由于机器含有一个维修区间,只需要维修不打断批次,工件加工就不会中断。按照以上对问题的分析,构造的具体算法如下: 第1步依据每批体积不超过车辆总体积的原则,利用FFD算法对所有工件进行分批,记总批数为b,工件批次集记为B={B1,B2,…,Bb}。 第2步计算每个批次Bk加工所需时间Pk,其中k=1,2,…,b。 第3步按照如下规则构造流水作业排序问题实例I(F2‖Cmax)。 任意批次Bk∈B在加工中心的加工时间为Pk,派送时间为T。 第4步利用Johnson算法最优的求解所构造的流水作业排序问题实例I,得到的排序记为π= 按照π中的批次顺序加工、交付批次,第一辆车派送奇数批次,第二辆车派送偶数批次; 同一批次加工不被维修打断,即若维修前不能加工完该批次,则该批次放在维修后加工; 每一个批次内工件加工顺序任意,若车辆可用时有多个批次可派送,则先加工完的先派送。 引理3由FFD-Johnson算法得到的Cmax,有以下结论: 证明若b=2,则Cmax=P+Δ+δ+T,显然成立;若b>2,按如下情况进行分类讨论: (1)维修在SPT与LPT之间 (2)维修在SPT中 (3)维修在LPT中 (1)Cmax=P+Δ+δ+T; (1)Cmax=P+Δ+δ+T; 定理2对于问题1,h(1)→D,k=1|v=2,c=1,T|Cmax,FFD-Johnson算法的界为2,且是紧界。 证明由引理4和引理5知定理第一部分成立。 众所周知,下列二划分问题是NP-难的。 本文研究了带有机器维修和工件派送的单机排序问题,不同体积的工件需要在带有维修区间的机器上加工,且加工不可中断,然后由固定容量的两辆同类车分批派送给单客户,目标函数是最小化最大完工时间。首先,根据装箱问题的NP-难性证明了该问题也是NP-难的;其次,提出解决该问题的近似算法;最后分析了算法的最坏情况界,并证明了该界是紧界。2 近似算法
3 最坏情况界分析




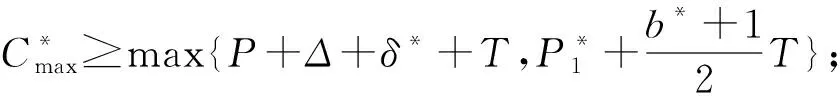
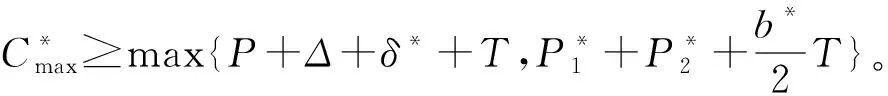


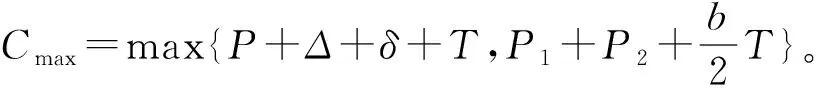

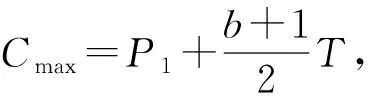
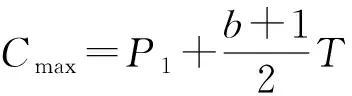
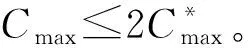
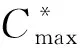

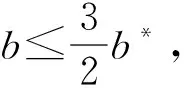





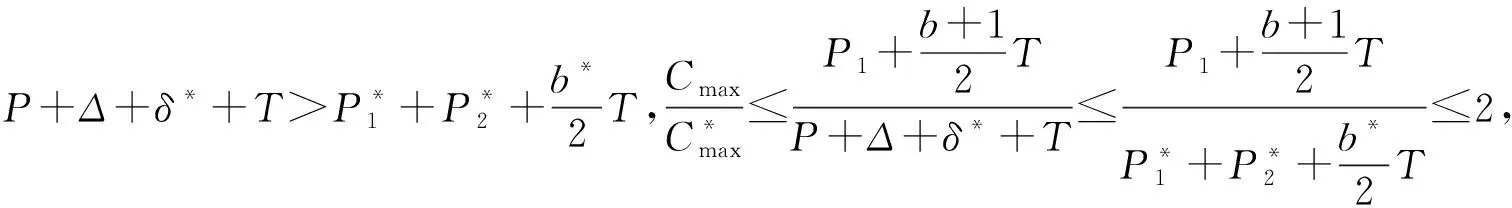

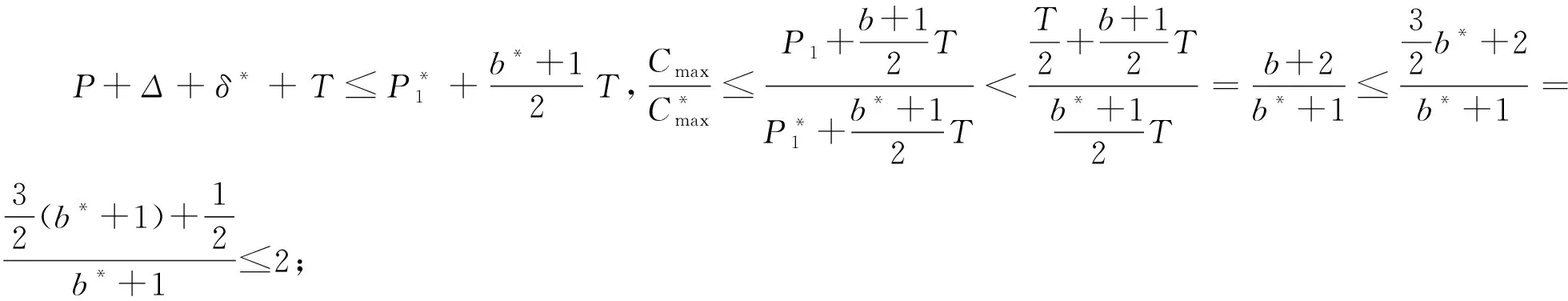
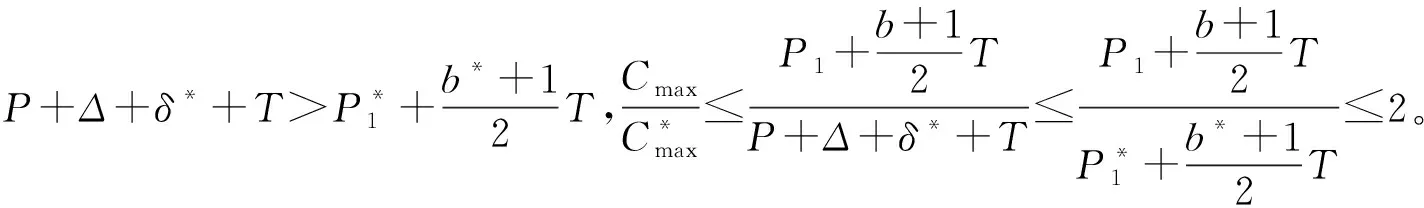
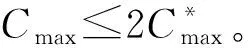
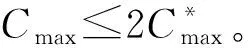
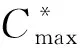
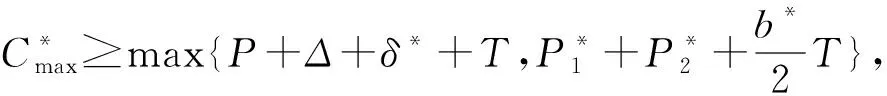

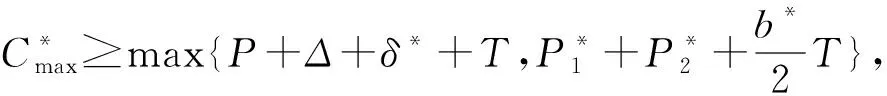
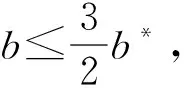


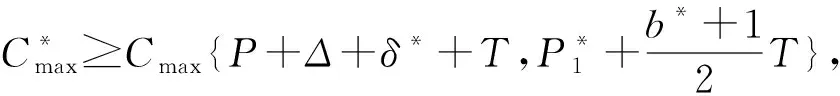
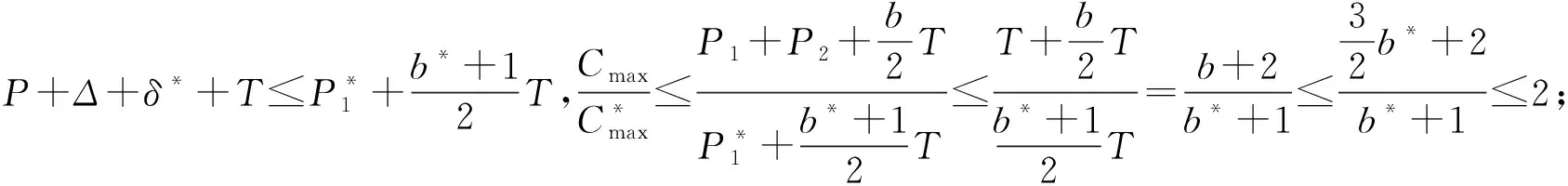
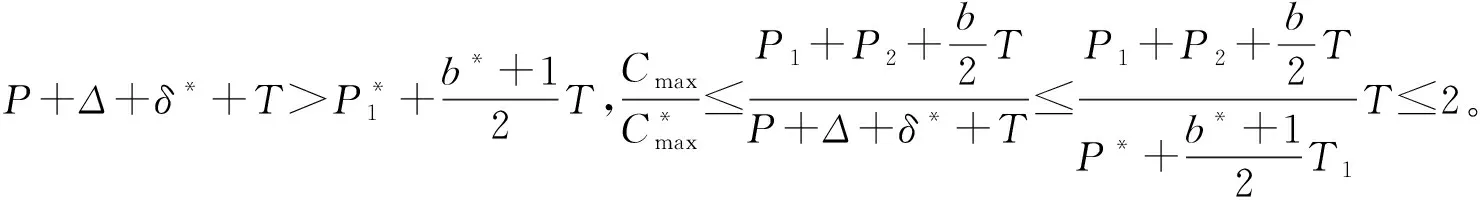
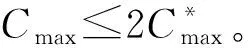
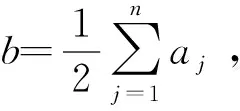
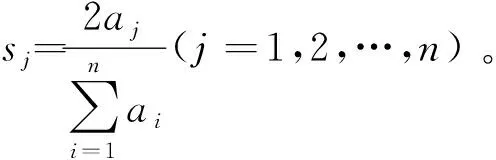
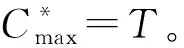
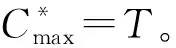
4 结论

