改进星形蜂窝结构面内动力学响应及能量吸收特性研究
胡锦顺, 林永水, 陈 威, 李晓彬, 吴卫国
(1.武汉理工大学 理学院,武汉 430063; 2.新材料力学理论与应用湖北省重点实验室,武汉 430063;3.武汉理工大学 交通学院,武汉 430063; 4. 武汉理工大学 绿色智能江海直达船舶与邮轮游艇研究中心,武汉 430063)
蜂窝结构因其优异性能,包括多孔性、轻质性和高比能量吸收性等,被广泛应用于航空航天、包装工程、汽车和人体防护等领域[1-2]。拉胀蜂窝结构具有传统蜂窝所不具有的负泊松比(NPR),使其具有较多优异的机械性能,如抗压性[3-4]、增强剪切模量[5]、高断裂韧性[6]、良好的抗冲击性[7-8]以及比能量吸收[9-10]。当受到冲击压缩载荷时,拉胀蜂窝可以使材料聚集在力的作用点附近,以抵抗冲击和吸收更多的冲击能量,在抗冲击防护结构领域有较大的应用前景。
拉胀蜂窝结构有多种类型,如手性结构[11-12]、内凹结构[13-15]和穿孔结构[16]。许多学者对常见的拉胀蜂窝进行了分析研究,取得了一系列的研究成果。Logakannan等[17]提出了一种新内凹拉胀结构,并通过实验和模拟验证了新结构比传统内凹结构具有更强的吸能能力。Wei等[18]通过实验和数值模拟研究了宏观和微观几何参数对星形蜂窝结构面内压缩行为的影响,发现减小正交排列比例和韧带长度可显著提高星形蜂窝结构的变形稳定性和能量吸收能力。Ma等[19]设计并研究了一种由反四手性蜂窝结构组成的拉胀阻尼器,发现拉胀结构可减轻阻尼器的重量,并具有较高的阻尼和一定的承载能力。
不同的拓扑结构对拉胀蜂窝的力学性能有很大的影响,各种结构有其自身的优点。为进一步提高拉胀蜂窝的吸能能力和力学性能,学者们设计了各种各样组合蜂窝。魏路路等[20]通过内凹六边形蜂窝与三边反手性蜂窝的结合得到一种内凹-反手性蜂窝结构,该结构与三边反手性蜂窝及传统蜂窝相比,表现出更加优异的能量吸收性能。虞科炯等[21]提出了一种引入正弦函数曲线的负泊松比蜂窝结构。研究表明振幅较小的正弦曲线负泊松比蜂窝结构具有更强的能量吸收能力,相对于内凹六边形蜂窝结构,能够显著降低峰值冲击力。Wei等[22]将三角形结构与传统的星形蜂窝结构相结合,提出了星形-三角形蜂窝结构,并通过理论和仿真研究了不同压溃速度下的动态压溃行为和能量吸收。发现与星形蜂窝结构相比,组合结构具有更高的面内刚度和压应力,并表现出更好的能量吸收。同样,为获得具有更高能量吸收能力的蜂窝结构,Wang等[23]将星形蜂窝(SSH)和双箭头蜂窝(DAH)相结合,设计了一种星形箭头蜂窝(SAH)。讨论了其面内静态性能和动态压缩性能,发现SAH具有比SSH和DAH更好的面内压缩性能和抗冲击性能。Xu等[24]提出了一种结合了传统六边形蜂窝和凹入式蜂窝的六边内凹蜂窝结构(AuxHex),研究了其变形特征和破坏模式。结果表明,AuxHex表现出更高的杨氏模量、抗压强度和吸能能力。
本文基于星形蜂窝结构(star-shape honeycomb,SSH),通过几何组合,引入了箭头形与方形结构,构建了一种改进星形蜂窝结构(improved star-shape honeycomb,ISSH)。旨在提高传统星形蜂窝结构的吸能特性与变形稳定性。讨论了其在低、中、高速下的变形模式和吸能特性,并基于典型胞元的变形特征,构建了其理论模型。
1 模型构建与可靠性分析
1.1 几何构型
基于星形蜂窝结构(SSH),利用箭头代替了其水平壁,并引入了与四个凹角接触的薄壁方形,构建了改进星形蜂窝结构(ISSH)。两种蜂窝结构如图1所示,其中H是胞元的高度(H=10 mm),S是胞元的长度,α是倾斜壁和水平方向之间的角度(α=π/6),π/2-α是倾斜壁和垂直方向之间的角度,t是胞元壁的厚度,L是方形的边长,L1为倾斜壁的长度,L2为水平壁的长度,L3为箭头形短边的长度。以胞元高度H与倾斜壁与水平方向夹角α为基准,其他几何特征可表示为
L=H(1-tanα)
(1)
L1=H/2cosα
(2)
L2=H/2
(3)
(4)
根据拉胀蜂窝的几何参数,SSH和ISSH的相对密度如下
(5)
(6)
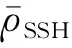

(a)
1.2 有限元模型
本文基于Abaqus软件建立有限元模型,如图2所示。上、下布置两个离散刚性板,下板为固定板,上板以恒定速度向下冲击。蜂窝自身与上下刚性板间定义了摩擦因数为0.2的通用接触。蜂窝整体沿x方向与y方向分别取11和15个胞元,其长度分别为156.5 mm与150 mm。面外长度取1 mm,为避免面外屈曲,模型中所有节点的面外位移均被限制。本文中蜂窝结构的相对密度都为0.18。对应蜂窝壁厚分别为tSSH=0.456 mm,tISSH=0.297 mm。采用S4R壳单元进行建模。基体材料为铝合金,并假定为理想弹塑性模型[25],密度ρs=2 700 kg/m3,弹性模量Es=68.2 GPa,泊松比ν=0.3,屈服应力σys=80 MPa。

图2 有限元模型(ISSH)
1.3 可靠性分析与模型验证
为了保证模拟的准确性,进行了网格灵敏度分析。图3显示了在准静态压缩下具有不同单元尺寸的蜂窝的等效应力-应变曲线。当单元尺寸减小时,等效应力明显减小并趋于收敛。根据结果,本文采取0.5 mm大小的网格进行有限元计算。为确保数值方法以及本文构建的有限元模型能准确模拟蜂窝结构的动态压缩行为,以文献的蜂窝模型(SAH)为例,构建了其数值仿真模型,各参数均与文献一致,在冲击速度为1 m/s下的比对如图4和5所示,本文模型的变形与文献的变形相似,且应力-应变曲线趋势基本一致。表明本文构建的模型以及数值方法的有效性。
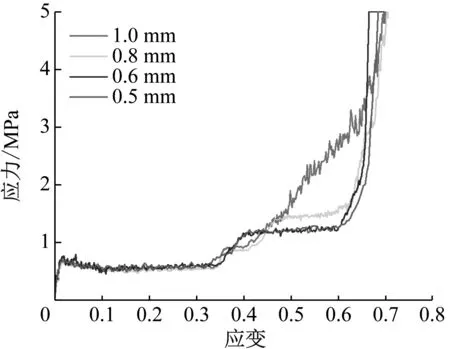
图3 不同单元尺寸的应力-应变曲线

ε=0.2

图5 SAH应力-应变曲线的比较
2 冲击载荷下变形模式与能量吸收分析
2.1 临界压溃速度
压溃速度是影响蜂窝动态压溃变形行为的一个重要参数。在不同的压溃速度下,蜂窝压溃端会产生不同的应力波。随着压溃速度的增加,应力幅值超过蜂窝体的屈服应力,蜂窝体出现局部塑性变形。基于“陷波”理论,在此临界阶段,引起塑性变形的压溃速度称为屈服速度或第一临界速度[26]
(7)
式中:εcr为初始应变(蜂窝到达初始峰值的应变);σ′(ε)=dσ/dε是在线弹性阶段的杨氏模量。
随着压溃速度的增加,蜂窝体的局部变形变得更加明显。冲击端局部变形更加明显,局部变形带以冲击波的形式由冲击端向固定端传播。在此临界阶段,引起塑性变形的压溃速度称为第二临界速度[27]
(8)
式中:σ0是蜂窝的静态屈服应力;εd是致密化应变。
致密化应变可由能量吸收效率方法确定
(9)
式中,能量效率η可由多胞材料所吸收的能量与相应名义应力的比值确定,即:
(10)
在本文中的计算中,定义最后的极大值点(即能量效率曲线开始迅速下降的点)所对应的名义应变为致密化应变,如图6所示。

图6 应力-应变及能量吸收效率曲线
2.2 低速载荷
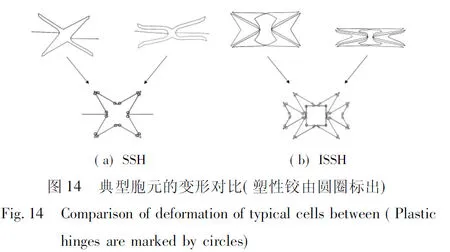
两种蜂窝结构在低速冲击下(1 m/s)的面内压溃行为如图7所示。当应变为0.1时,SSH下部先发生收缩变形,星形胞元壁沿对角线方向贴合。当应变增加到0.3时,可以发现贴合的星形胞元逐渐向上扩散,星形胞元大多被压成菱形胞元。随着进一步的压缩,菱形胞元也被压溃,同时伴随少量星形胞元存在于蜂窝上下部分。当星形胞元与菱形胞元都被压溃完毕时,蜂窝成为完全密实的结构。不同于SSH,当ISSH压缩应变达到0.1时,蜂窝在左右两侧发生反对称收缩,由于胞元中心存在方形结构,星形胞元无法转变为菱形胞元,胞元壁只能随着压缩发生转动。当应变增加到0.3时,蜂窝的中下部已经基本收缩完毕,并逐渐向蜂窝上方扩散。随着进一步压缩,蜂窝侧方基本不发生收缩,蜂窝整体形成规整的方形,胞元逐渐压溃,直至致密化。总体来说,相对于SSH结构,ISSH的变形更加均匀稳定。

两种蜂窝结构在低速冲击下的应力应变曲线如图8所示。SSH的应力应变曲线可分为弹性区、平台区和致密化区三部分。弹性区出现在蜂窝小变形阶段。在平台区,随着应变的增加,伴随着更多胞元壁的屈服,应力在此区间缓慢增大。在致密化区,应力快速增大。ISSH的应力应变曲线可分为弹性区、第一平台区、过渡区、第二平台区和致密化区这五部分。在弹性区与致密化区,曲线变化与SSH比较一致。在弹性区后,随着星形胞元斜壁的屈服,形成了第一平台区。在过渡区,随着屈服的胞元壁增多,应力也缓慢增大。随后出现第二平台区。相较于SSH,ISSH的应力应变曲线存在着稳定的双平台区,且有着较大的应力值。
图8 低速冲击(1m/s)下SSH与ISSH的应力-应变曲线
2.3 中速载荷
图9为中速冲击下(20 m/s)的变形模式。当应变为0.1时,对于SSH,由于存在一定的惯性效应,变形首先发生在冲击端,其他位置的胞元基本上保持不变。当应变增加到0.3时上方胞元压溃,下方星形胞元逐步变为菱形胞元。随着进一步压缩,压溃范围向下扩散,直至蜂窝密实化。对于ISSH,变形同样首先发生在冲击端,而后逐渐向下传递,直至密实化。在压缩过程中,两种蜂窝结构都表现出一定程度的收缩(NPR效应),SSH随着压缩应变的增大,由上往下逐渐收缩,而ISSH则是在冲击端下方开始由上往下逐渐收缩。图10示出了在中速冲击下的应力-应变曲线,与低速冲击不同(图8),在初始压溃阶段,由于胞壁的局部逐步坍塌,应力表现出振荡行为。随着应变的增加,应力逐渐稳定。对于ISSH,曲线在应变为0.7左右时,表现出一段范围较小的平台区。


图10 中速冲击(40 m/s)下SSH与ISSH的应力-应变曲线
2.4 高速载荷
如图11所示,在高速(100 m/s)冲击下,惯性效应明显,从冲击端开始胞元被逐级压溃。SSH与ISSH的变形相似,压缩带均较为规整,其中,SSH在压缩过程中仍具备一定的收缩变形,而ISSH基本上观察不到NPR效应。由于单元的周期性变形,应力-应变曲线(图12)中存在一些峰值应力,其数量约等于胞元层数。同时,SSH与ISSH的应力在恒定值附近波动,直到胞元壁完全重叠在一起,压溃应力迅速增加。
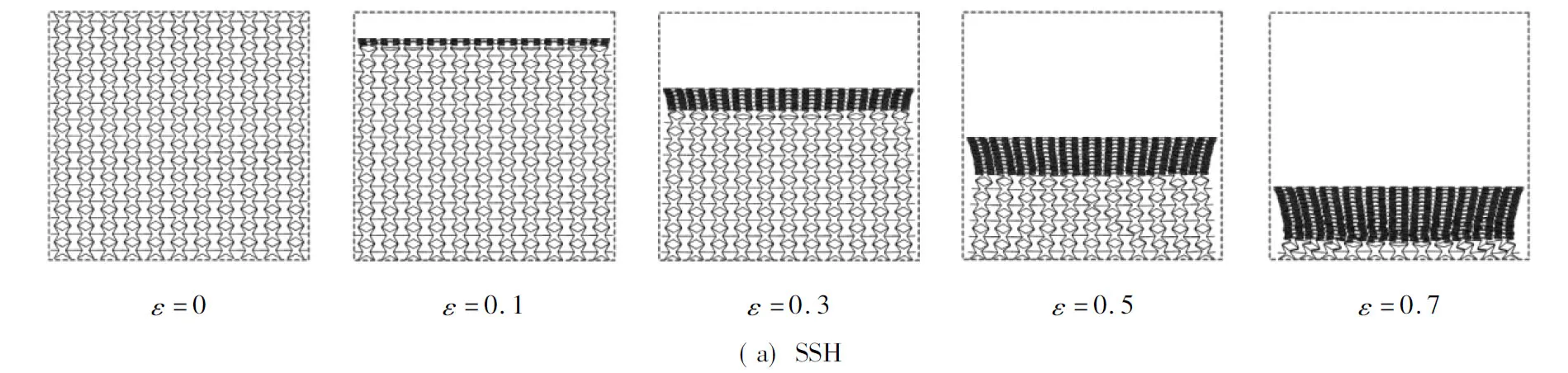

图12 高速冲击(100 m/s)下SSH与ISSH的应力-应变曲线
2.5 能量吸收
比吸能(SEA)用于评估某一结构吸收能量的能力,通常可表示为
(11)
式中,σ与ε分别为名义应力与名义应变。

图13 两种蜂窝在不同速度下的比吸能

表1 两种蜂窝在不同速度下的比吸能比较(取致密化之前)
3 理论分析
基于以上分析,在低速载荷下,ISSH具有比SSH应力更高的双平台应力阶段,平台应力是能量吸收的一个关键参数。为明确几何参数对平台应力的影响,从理论上指导结构优化设计,本文首先构建了理论模型来推导低速载荷下的两个平台应力(由于速度较小,视为准静态压缩,不考虑速度效应)。由于组合蜂窝的坍塌过程较为均匀,且具有周期特性,基于典型胞元进行分析。图15为胞元在两个平台阶段的变形形态。由于外力在蜂窝上所做的功等于蜂窝壁上塑性铰所消耗的能量和方形薄壁所吸收的能量,基于能量守恒推导两个平台应力。
初始和第一平台段结束时的胞元形态如图15(a)和(b)所示。以1/4胞元为例,倾斜壁AB同时绕A点和B点逆时针旋转,直至其到达水平方向。类似地,倾斜壁BC围绕点B和C旋转,直到与壁BC与CD接触,而倾斜壁CD保持不变,没有变形和旋转。基于几何对称性,其他胞元壁的变形过程与1/4胞元壁相似。在图15(a)中,16个塑性铰出现在由红色圆圈突出显示的典型胞元中。同时,由于方形和倾斜壁之间的公共节点接触,方形在公共节点两旁存在8个塑性铰。从(a)到(b),壁AB旋转一个角度Δφ,壁BC旋转一个角度Δφ,方形中塑性铰旋转度数为Δδ。假设方形中各塑性铰旋转角度一致且倾斜壁的长度保持不变。根据单元的几何关系和变形过程,适当考虑胞元厚度,塑性铰的度数计算如下
Δφ=α
(12)
Δφ=α
(13)

在第一平台阶段,外力在胞元上所做的功为
wp=σp1s0bΔy
(14)
(15)
式中:s0为胞元初始横向长度;σp1为第一平台应力;b为单位面外长度;Δy为外力方向的相对位移;H0为胞元的初始高度;H1为第一平台阶段结束时胞元的高度。
在从图15(a)到(b)的变形过程中,总的能量耗散由两部分组成:倾斜胞壁中塑性铰的能量耗散E1和压缩下方形胞壁中塑性铰的能量耗散E2。对于倾斜胞壁的能量耗散,可表示为
E1=8M1Δφ+8M1Δφ
(16)
其中矩形截面梁的塑性极限弯矩为M1=σysbt2∕4。对于方形的能量耗散,可表示为
(17)
式中,Δx为侧向压缩位移,表示为
Δx=H(2-tanα-1/cosα)
(18)
根据能量守恒,有:
E1+E2=Wp
(19)
综上,可得到ISSH在1 m/s的低速冲击下的第一平台应力的表达式为
(20)
当倾斜壁与箭头形长边贴合时(图15(b)),应力开始增加,第二平台应力阶段开始。在第二个平台阶段,对于星形结构,斜壁BC围绕点B和C旋转,水平壁AB仅在垂直方向移动,没有旋转或弯曲变形;对于方形结构,塑性铰从原有的8个,增加到12个,在图15(c)中标出;对于箭头形结构,长边CD围绕点C和D旋转,短边DE围绕点D与E旋转,直到结构致密。
考虑到厚度对几何参数和变形的影响,胞元在第二应力阶段的初始高度和致密化高度可以表示为
H1=Htanα+2t
(21)
H2=11t
(22)
胞元的星形胞壁和箭头形长边的塑性铰转动角度为
Δφ′=α-arcsin(H2/2L1)
(23)
胞元的箭头形短边的塑性铰转动角度为
Δφ′=π/2-α-arcsin(H2/2L1)
(24)
胞元的方形取1/4构型进行分析,边AF围绕点A和F旋转,边CF围绕点C和F旋转。根据方形的变形,F点的塑性铰转动角度为Δδ′=π/2,则易知1/4构型中塑性铰转动角度为π。
第二平台应力仍然可以由能量守恒得到,其表达式如下
8M2Δφ′+8M1Δφ′+8M1Δδ′=σP2S1b(H1-H2)
(25)
(26)
式中:重合斜壁的塑性极限弯矩M2=2M1;σP2为第二平台应力;S1为第二平台阶段开始时胞元的长度。
因此,第二平台应力σP2的表达式为
(27)
为验证上述理论分析在低速冲击条件下平台应力的准确性,对具有不同相对密度ISSH的理论计算和数值模拟进行比较,结果如图16所示。两段平台应力的理论分析结果与数值仿真结果吻合较好。表2列出了不同相对密度和冲击速度下理论预测和模拟的具体值与相对误差。最大相对误差的绝对值为8.1%,表明构建的理论分析模型可在误差允许范围内准确预测ISSH的两个平台应力。
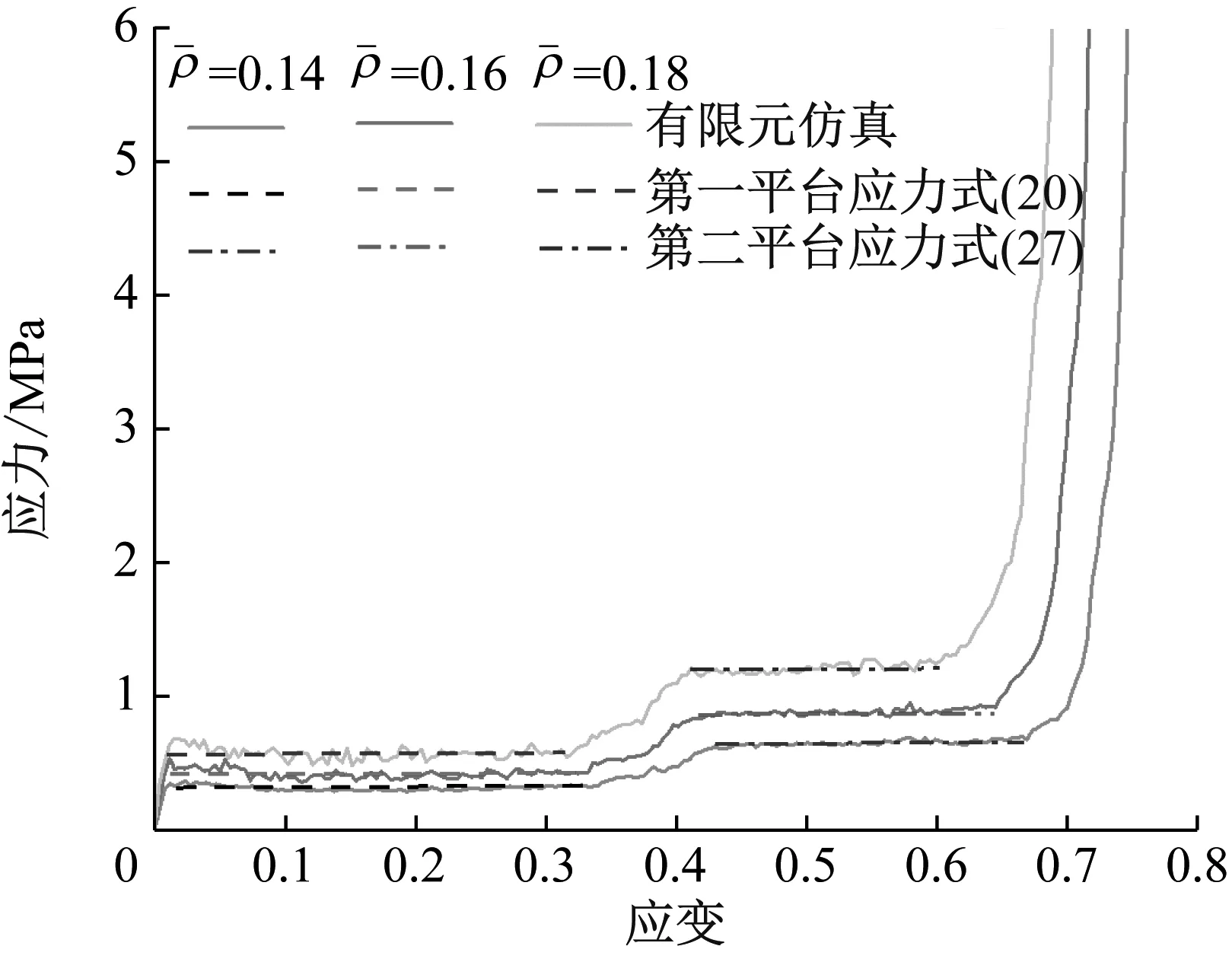
图16 低速冲击(1 m/s)下ISSH两个平台应力的理论和
根据周期性变形的特点与动量定理建立了速度载荷下平台应力的理论分析模型。以高速载荷为例,图17给出了理论分析的示意图,其中以沿加载方向具有两个相邻单元的典型单元作为研究对象如图17(a)所示。在塌陷开始时,上部单元首先压溃,而下部单元保持不变如图17(b)所示。随后,下部单元重复上部单元的变形如图17(c)所示。在从图17中的(b)到(c)的周期性变形期间,典型单元的动量变化可以表示为
(28)

(29)

表2 低速冲击(1 m/s)下ISSH两个平台应力的理论和数值模拟的结果对比

在t2时刻,上部胞元整体以恒定速度v向下运动,则此时胞元的动量可表示为
(30)
PS=8ρsL1btv
(31)
PA=4ρsL1btv+4ρsL3btv
(32)
PR=4ρsLbtv
(33)
式中:PS为星形部分动量;PA为箭头形部分动量;PR为方形部分动量。
根据动量守恒,可以得到
bS0(σ1-σ2)(t1-t2)=ΔP
(34)
(35)
式中:σ2为准静态加载下胞元的平均平台应力;σ1为高速加载下胞元的平均平台应力;T为胞元逐层压溃的循环时间。
对于准静态加载下胞元的平均平台应力σ2,引入常数λ可表示为
(36)
如图8所示,在低速下,第一平台应力的区间大于第二平台应力的区间,所以本文中,常数λ取0.6以估算准静态加载下的平均平台应力。综合上式,速度加载下胞元的平均平台应力可表示为
(37)

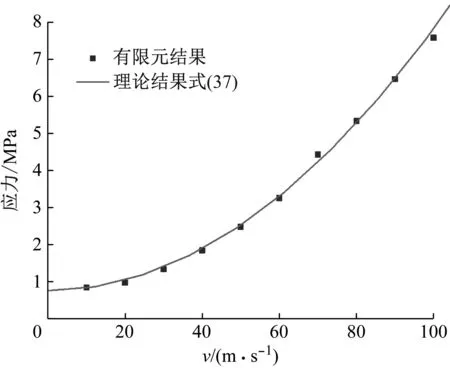
图18 不同冲击速度下ISSH平台应力理论结果与
4 结 论
为提高SSH的能量吸收,基于几何组合,提出了一种改进星形蜂窝结构。借助于理论和数值方法研究了其压溃特性和能量吸收能力。得出以下结论:
(1) 在低速载荷下,相比于SSH,ISSH的变形更稳定且应力-应变曲线呈现两个稳定的平台应力阶段。这可以解释为箭头形和方形薄壁结构极大的增加了变形的稳定性,提高了平台应力,促进了蜂窝结构在低速载荷下的能量吸收(比吸能提高了30.0%)。在高速载荷下,受惯性效应影响,应力-应变曲线呈现剧烈波动。由于相对密度相同,两种蜂窝的吸能能力逐渐靠近。但ISSH仍然表现出较为优异的能量吸收能力(比吸能提高了10.3%)。在中速荷载下,两种蜂窝兼具低速和高速载荷的特性,不仅产生整体变形,还会像在高速荷载下一样发生局部压溃。且蜂窝应力-应变曲线前期剧烈波动,而后逐渐稳定。其能量吸收同时受到塑性耗散与动量因素的影响,其比吸能相较于SSH提高了72.3%。
(2) 构建了准静态加载以及速度载荷下平台应力的理论分析模型。塑性耗散理论,给出了准静态加载时第一平台应力和第二平台应力的表达式。基于动量守恒,给出了速度载荷下的平台应力。理论分析结果与数值模拟结果吻合较好,证明理论模型可以预测ISSH的平台应力。

