近场地震作用下近海单桩风机动力响应分析

徐亚洲， 段 静

(西安建筑科技大学 土木工程学院，西安 710055)

近年来，随着风能开发技术的逐渐成熟，海上风机装机容量不断攀升。全球风能协会(Global Wind Energy Council，GWEC)在2020年度报告中指出，2019年全球海上风电创纪录新增装机容量6.1 GW，我国以2.4 GW再次成为海上风电新增装机最多的国家[1]。但是，我国风能资源丰富的东南沿海位于环太平洋地震带，复杂的环境荷载和频发的地震灾害将制约风电的发展。因此，开展近海风机抗震研究具有重要的现实意义。

国内外学者对地震作用下风机结构的动力响应做了大量研究。Bozeos等[2-3]将风轮和机舱简化为集中质量点，建立简化有限元模型，对风机塔架进行了地震响应分析，指出在进行结构设计时应考虑地震作用。戴靠山等[4]利用ABAQUS软件建立某1.5 MW风机精细化模型，探讨了风机塔筒在极端动荷载作用下的破坏规律。贺广零等[5-6]基于多体动力学基本理论，建立了风机高塔系统“桨叶-机舱-塔体-基础”一体模型，研究发现考虑SSI效应在一定程度上会放大结构的响应。杨阳等[7]基于FAST软件预留接口，采用Wolf方法[8]建立风机土-结相互作用模型，分析了风机在湍流风和地震联合作用下的动力响应。李颖等[9-10]通过数值模拟和实验发现，风、波浪和地震联合作用时风机响应存在明显的耦合效应。席仁强等[11]分析了风浪荷载对海上风机地震响应的影响。考虑到近场脉冲型地震动对结构破坏性更大，徐亚洲等[12-14]开展了某2 MW风机的缩尺振动台实验，分析了近场地震动速度脉冲对风机动力响应的影响。

上述研究多集中于陆上风机在近场或远场地震下的动力响应，而对近海风机在近场地震下的研究较少。考虑到近场地震中存在脉冲型地震动，其伴随较大的速度脉冲和具有较长的周期，对风机这类长周期结构有较大的破坏力。并且近海风机所处环境复杂，常年受到风浪荷载作用，地震发生时风机将存在更多的安全隐患。因此，有必要研究风-浪-地震耦合效应以及速度脉冲对近海风机动力响应的影响。

针对以上问题，本文基于开源软件FAST[15]自编程开发地震分析模块，形成具有地震载荷计算功能的耦合仿真软件FAST-S，并利用Seismic和ABAQUS来验证该模块的计算精度和可靠性。随后通过软件预留子程序开发土-结相互作用模块，建立考虑SSI效应的5 MW近海单桩风机模型，并分析风、波浪和地震之间的耦合效应以及研究近场地震动速度脉冲对风机支撑结构动力响应的影响。

1 FAST-S的开发与验证

1.1 FAST仿真平台介绍

FAST是美国可再生能源实验室(National Renewable Energy Laboratory，NREL)开发的专用于水平轴风机仿真计算的开源软件。早期版本FAST v7集气动模块、水动模块、伺服控制和结构计算模块于一体。其中，气动模块通过叶素动量理论和广义动态尾迹理论计算气动载荷，并考虑动态失速模型对气动力的修正；水动模块采用Airy波浪理论和Morison方程计算水动力；结构模块基于刚柔混合多体动力学和线性模态法，通过Kane方法建立动力学方程，使用四阶Runge-Kutta法和Adams-Bashforth预测-校正方法对方程求解。该软件具有较高的认可度，被各国研究学者广泛使用。

FAST使用Kane方法建立动力学方程，然后通过数值积分进行求解。对于具有p个自由度的风机系统，其动力学方程可以表示为

(1)

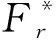
其中，广义惯性力受质量、线性加速度和角加速度的影响。所有具有质量的部件对风机系统所受广义惯性力的贡献如下

(r=1,2,…,p)

(2)

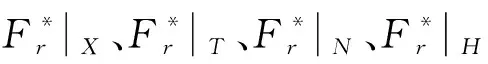
广义主动力由作用在风机系统上的几种不同类型的力产生。这些力包括：气动力、水动力、重力、柔性体的弹性恢复力等。其表达式如下所示

Fr=Fr|aero+Fr|hydro+Fr|grav+Fr|elastic+Fr|others

(r=1,2,…,p)

(3)

当计算出所有的广义主动力和广义惯性力，将式(2)和(3)代入式(1)得到风机系统动力学方程，其矩阵形式为

(4)

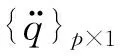
该方程求解时采用四阶Adams-Bashforth预测-校正方法，由于该方法不是自发性的，前四个时间步采用四阶Runge-Kutta法求解。

1.2 地震分析模块的开发

针对FAST早期版本无地震分析模块这一问题，密苏里科技大学Prowell在NREL支持下设计和开发了地震分析软件Seismic[16]，并采用OpenSees验证了其计算精度和可靠性。Seismic通过修改子程序UserPtfmLD，利用阻尼弹簧振子来模拟地震引起的基底运动。该方法具有一定的局限性：阻尼弹簧振子的频率和阻尼比严重依赖于经验取值，对于不同的风机，其计算结果会受到影响；该软件的开发思路目前不支持土-结相互作用，对位于软弱土层的近海风机适用性较低，多用于固定的陆上风机地震仿真计算。

为打破上述局限，本文借鉴结构计算模块对气动力和水动力的处理方法，将地震作用以等效地震力的形式施加在风机结构上，来实现在FAST v7中添加地震分析功能。该方法避免了经验取值带来的计算误差并支持土-结模型的开发，同时适用于陆上和海上风机的抗震分析，具有更高的适用性。

二次开发的思路是将地震荷载以主动力的形式施加在风机结构上。地震力所产生的广义主动力Fr|seismic由以下几部分组成

Fr|seismic=Fr|seisX+Fr|seisT+Fr|seisN+Fr|seisH+Fr|seisB

(r=1,2,…,p)

(5)

式中，Fr|seisX、Fr|seisT、Fr|seisN、Fr|seisH、Fr|seisB分别为作用在风机系统基础平台、塔架、机舱、轮毂和叶片上的地震力所产生的广义主动力。其具体计算公式如下：

(6)

(7)

(8)

(9)

(10)

基于上述公式的推导，通过修改和扩充FAST.f90、FAST_IO.f90和FAST_Mods.f90源文件，将地震力产生的广义主动力Fr|Seismic代入式(1)的广义主动力项中，即可实现地震分析模块的添加，形成具有地震计算功能的耦合仿真软件FAST-S。该软件各模块的逻辑结构如图1所示。

图1 FAST-S

1.3 地震分析模块的验证

选择Prowell开发的地震分析软件Seismic和有限元软件ABAQUS来验证地震分析模块的计算精度。由于Seismic多用于陆上风机抗震分析，因此选择NREL 5 MW[17]陆基风机为验证机型，以1940 Imperial Valley地震动作为激励，在400 s时输入地震动，计算风机在停机状态下的动力响应。

图2为三种软件计算得到的风机塔架纵向时域响应。从图中可知，FAST-S与其他两个软件的计算结果整体吻合较好，该软件开发的地震分析模块具有较高的计算精度，可用于海上风机地震动力响应分析。

图2 风机塔架时域响应对比

2 风机模型和外部激励

2.1 风机模型

FAST v7中建立的风机模型默认为刚性基础，忽略了土-结相互作用。对于近海单桩风机，通常海床有较厚的淤泥和软土质，刚性基础建模过于理想化。另外，软弱基础会增大结构的固有周期，使其更接近环境荷载的频率，这可能导致结构动力响应的增大。因此需要进一步在FAST-S基础上二次开发建立考虑SSI效应的风机模型。模型采用Jonkman等[18]在OC3项目中提出的适用于水深20 m的5 MW近海单桩风机，风机具体参数见文献[17]。风机模型和土层分布信息如图3所示，图中γ为场地土有效重度，φ为内摩擦角。

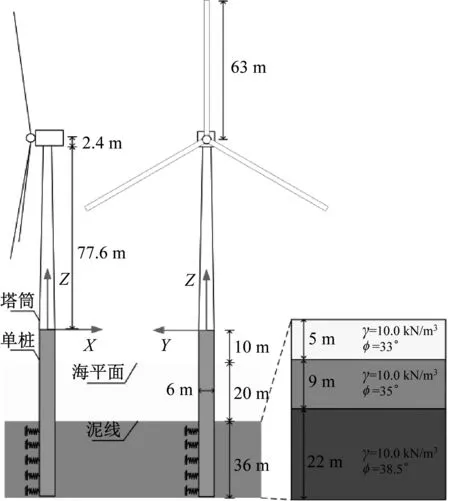
图3 风机模型和土层分布

Passon[19]将上述土层离散为37个沿竖向均匀分布的线性弹簧(distributed springs，DS)，并根据p-y曲线初始切线刚度换算得到每个线性弹簧的刚度，如图4所示。文中采用分布式线性弹簧模拟土-结相互作用，建立单桩风机线性SSI模型。当确定了没入泥土深度为z处的弹簧刚度kz和结构位移向量Xz，则此处土壤反作用力Fz可以表示为

Fz=kz·Xz

(11)

要实现上述土-结模型，需用到HydroCalc.f90源文件中预留的虚拟子程序UserTwrld。该程序用于给风机支撑结构施加外部荷载，并将荷载以弹簧力的形式耦合到式(1)中。通过修改子程序UserTwrld，建立式(11)所示的荷载模型，在FAST-S中增加土-结相互作用模块。首先利用上个时间步的结构位移和定义的弹簧刚度计算施加在桩基上的荷载，并将荷载传递到结构计算模块进行求解，得到当前时间步的结构位移，然后将结构位移反馈给子程序并结合弹簧刚度进行下个时间步的计算。如此反复，使FAST-S可考虑SSI效应。

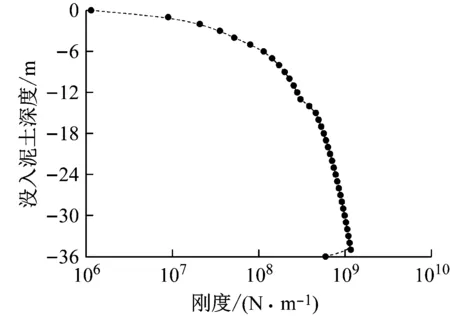
图4 弹簧刚度分布

采用NREL开发的Bmodes[20]软件计算了考虑SSI效应的风机支撑结构纵向(fore-aft)和侧向(side-side)前两阶振型的固有频率，如表1所示。与文献[21]对比可知，该模型具有较高的准确性，可用于后续的计算分析。

表1 支撑结构固有频率

2.2 外部激励

2.2.1 地震动

一般认为断层距小于20 km的地面运动为近场地震动，峰值速度(PGV)和峰值加速度(PGA)的比值大于0.2时带有速度脉冲。根据该规则从太平洋地震工程研究中心(PEER)强震数据库选取16条近场地震动记录[22]，其中脉冲型地震动和非脉冲型地震动各8条，如表2所示。

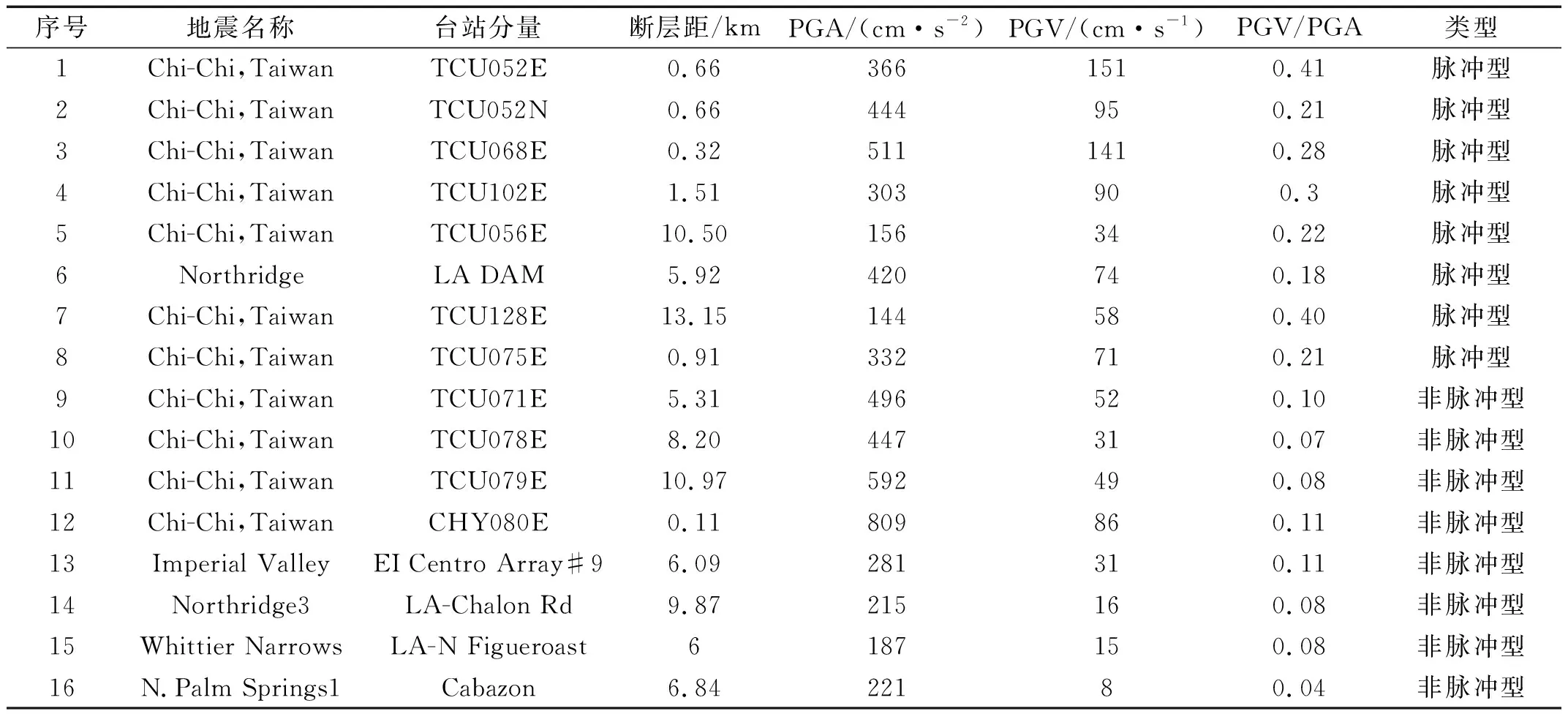
表2 近场地震动特性参数

2.2.2 湍流风模型

Turbsim[23]开源程序由NREL开发，用于生成FAST所需的随机三维湍流风场。该软件包含多种风谱模型，采用IEC Kaimal谱来模拟湍流风场，其功率谱密度函数表达式为

(12)

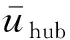
设定湍流风场以轮毂为中心，大小为145×145 m，轮毂高度处平均风速为额定风速11.4 m/s，湍流强度类型为B，采用指数型风廓线，幂指数取0.14[24]。通过Turbsim软件模拟得到湍流风场，其轮毂高度处风速时程曲线如图5所示。

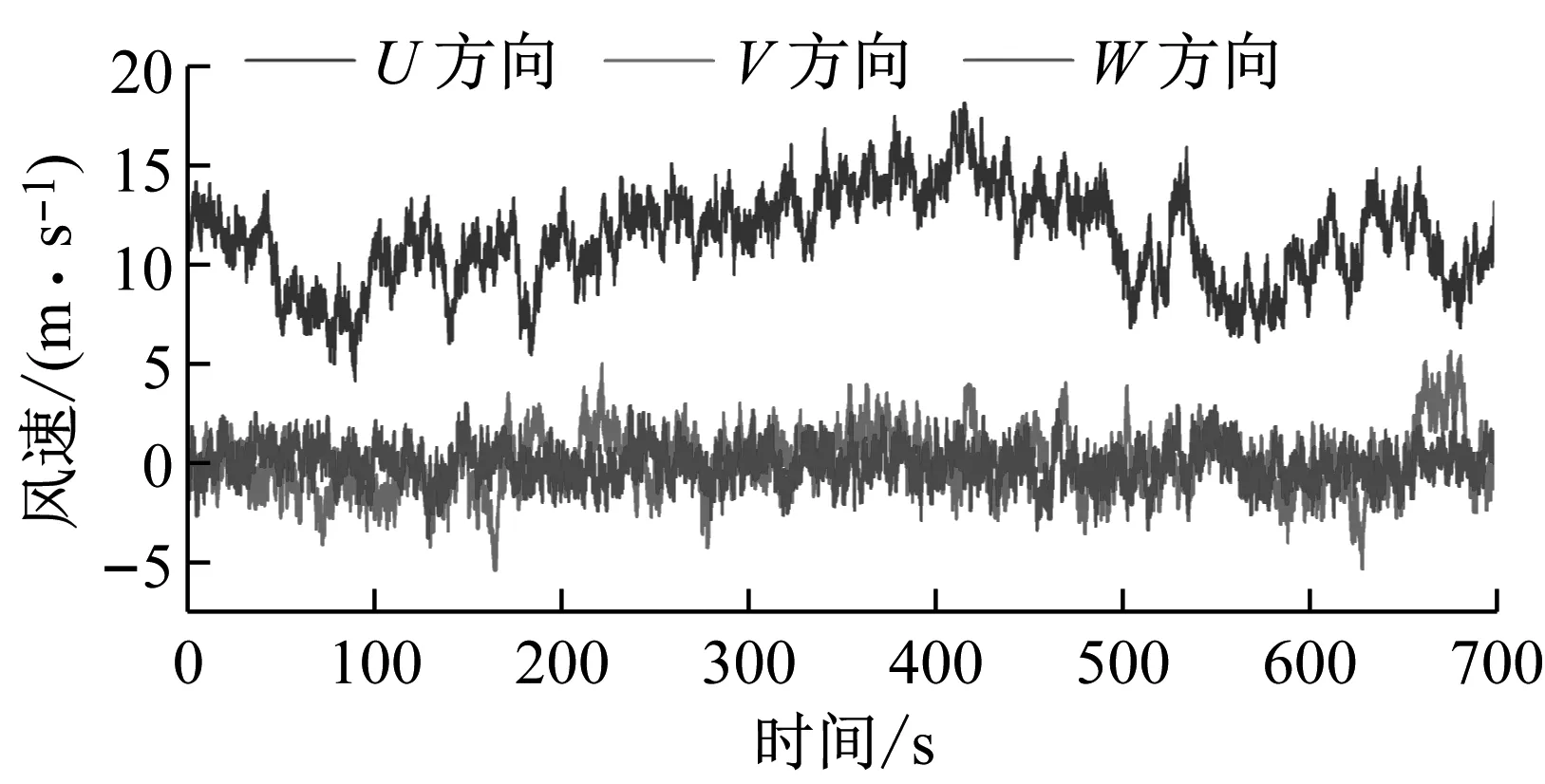
图5 轮毂处风速时程曲线

2.2.3 波浪模型

非规则波浪时域数据可采用FAST水动模块进行模拟。首先基于波浪谱模型通过谐波叠加法得到波面高程，然后采用Airy波浪理论计算水质点的水平速度和加速度，从而模拟出波场。文中采用JONSWAP波浪谱模拟波高时程，其功率谱密度函数可表示为

(13)

式中:f为波浪频率;f=1/T;T为波浪周期。fp为谱峰频率，fp=1/TP，TP为谱峰周期。g为重力加速度。σ为谱宽参数，f≤fp时，σ=0.07；f>fp时，σ=0.09。a为归纳的Phillips常数，γ为谱峰提升因子，二者由下面公式确定。

(14)

(15)

基于JONSWAP波浪谱和Airy波浪理论通过FAST水动模块生成有效波高为6.3 m，谱峰周期为10.5 s的波场，其波高时程曲线如图6所示。

图6 波高时程曲线

3 风-浪-地震耦合效应分析

基于上述风机模型和外部激励，设置5个工况分析风、波浪和地震之间的耦合效应，如表3所示。其中，风条件为轮毂高度处平均风速为11.4 m/s的湍流风，波浪条件为有效波高为6.3 m、谱峰周期为10.5 s的非规则波浪，地震为1号地震动。各工况仿真时长为600 s，在400 s时加入地震动，假定风、波浪和地震同向且均沿风机纵向作用。

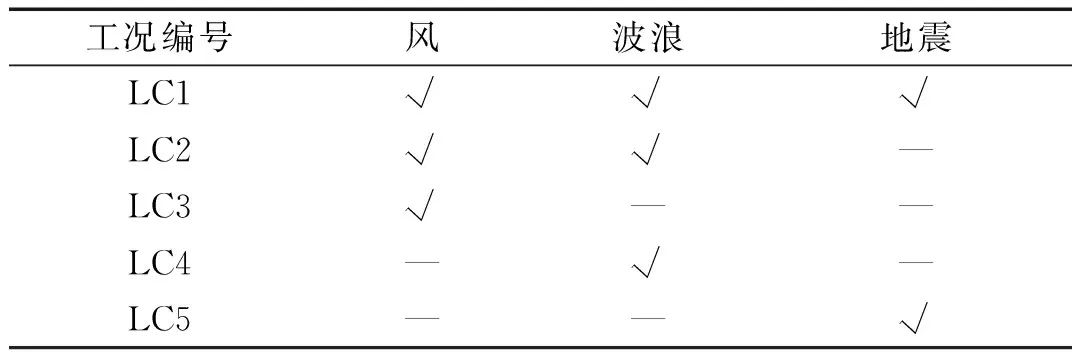
表3 动力分析工况

5 MW单桩风机在工况LC1、LC2和LC5下的塔顶位移、加速度时程曲线如图7所示。对于风、波浪和地震共同作用工况LC1，强震到达前(t<430 s)，风机仅受风浪荷载作用，塔顶位移和塔顶加速度分别在0.5 m和0附近小范围波动；强震到达后(t>430 s)，塔顶位移和塔顶加速度急剧增大，峰值分别达到1.99 m和3.83 m/s2。对于仅地震作用工况LC5，强震使塔顶位移和塔顶加速度均出现剧烈振荡，峰值分别为1.84 m和4.53 m/s2。分析表明，地震荷载会诱导塔顶发生较大振动，使塔顶位移和加速度急剧增大。

图7 塔顶位移、加速度时程曲线

此外发现，工况LC1在强震后塔顶位移和塔顶加速迅速衰减，470 s左右时程曲线与工况LC2基本一致，且在风浪荷载作用下小范围变化；工况LC5在强震后塔顶位移和塔顶加速度在自身结构阻尼影响下呈现较慢的衰减趋势。另外，工况LC1对应的塔顶位移和塔顶加速度变化幅度分别为2.59 m和6.76 m/s2，相较于工况LC5对应的3.56 m和8.86 m/s2，减小了27%和24%。出现上述现象的主要原因是气动阻尼和水动阻尼增大了结构系统的阻尼，从而加速了地震能量的耗散，抑制了塔顶振动。

图8为塔顶位移、加速度幅值谱。对于塔顶位移，工况LC1和LC2在0处有明显幅值且大于一阶固有频率处的幅值。0处的幅值与湍流风中平均风分量大小直接相关，表示直流分量。这一结果表明，塔顶位移受平均风影响显著。对比三个工况发现，地震工况LC1和LC5的塔顶位移和加速度在一阶固有频率处均有明显幅值，且仅地震作用时的幅值大一个量级。此外，仅地震作用时塔顶加速度在二阶固有频率处也存在明显幅值，而风、波浪和地震共同作用时此处的幅值不明显，这是因为风浪荷载起了抑制作用。以上现象也进一步证实了风浪荷载耗散了结构振动能量，对抑制塔顶振动有一定积极作用。

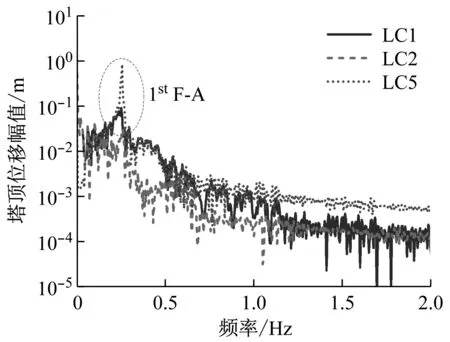
(a)

另外对比发现，地震参与工况LC1和LC5塔顶位移和加速度在一阶固有频率处幅值均大于风浪作用工况LC2，地震作用下结构一阶振动模态更大程度被激发。此结果也进一步说明了地震荷载加剧了塔顶振动，增大了结构一阶模态振型对塔顶位移和加速度的贡献。

图9给出了不同高度处支撑结构的最大剪力和弯矩。从图中可知，各种工况的最大剪力和弯矩随高度先增大后减小，在泥线(Mudline)以下出现最大值，在海平面(MSL)以上近似线性减小。其中，工况LC1和LC5因地震作用的影响，其剪力和弯矩远大于无地震工况，特别是泥线以下的单桩基础。因此，设计时应加强单桩的强度来满足地震条件下风机支撑结构受到的剪力和弯矩。此外，从图中还发现，风、波浪、地震单独作用产生的最大剪力和弯矩线性叠加(LC3+LC4+LC5)后，其数值明显大于风、波浪和地震耦合作用工况LC1的值。对于本节算例，风、波浪、地震耦合与线性叠加两种情况，泥线处最大剪力和弯矩分别相差102%和57.2%。这一结果说明，风机在受到风、波浪和地震共同作用时，气动载荷、水动载荷和地震载荷之间存在非线性耦合关系，线性叠加将过高估计风机结构受到的剪力和弯矩，计算时应充分考虑风-浪-地震耦合效应。

(a)

4 速度脉冲对风机支撑结构动力响应的影响

研究近场地震动速度脉冲对停机和正常运行状态下风机动力响应的影响。其中，停机状态下的风机保持顺桨并关闭发电机，仅受到地震作用；正常运行状态下的风机正常运转，受到湍流风、非规则波浪和地震同时作用。风条件为轮毂高度处平均风速为11.4 m/s的湍流风，波浪条件为有效波高为6.3 m、谱峰周期为10.5 s的非规则波浪。将所选16条地震动加速度幅值按8度罕遇时程分析所用加速度峰值调幅至0.4g，并进行时域仿真计算。仿真时长取600 s，时间步长取0.001 s，为消除瞬态响应的影响，第400 s时加入地震动，假设风、波浪和地震同向且均沿风机纵向作用。

图10为脉冲型地震动(TCU052E)和非脉冲型地震动(TCU071E)作用下风机支撑结构的动力响应时程曲线。从图中可以观察到，两种运行状态下风机的塔顶位移、塔顶加速度和泥线处弯矩存在很大差异，脉冲型地震动作用下其幅值明显更大。

表4和表5分别给出了脉冲型地震动与非脉冲型地震动作用下两种运行状态风机的塔顶位移、塔顶加速度和泥线处弯矩最大值及其平均值。对于停机状态下的风机，脉冲型地震动作用下塔顶位移、塔顶加速度和泥线处弯矩最大值的平均值分别为184.26 cm、4.76 m/s2和238.86 MN·m，相较于非脉冲型地震动作用下的25.87 cm、1.80 m/s2和109.99 MN·m，分别增大了612.25%、164.44%和117.17%；对于正常运行状态的风机，脉冲型地震动作用下塔顶位移、塔顶加速度和泥线处弯矩最大值的平均值分别为165.26 cm、3.29 m/s2和220.96 MN·m，相较于非脉冲型地震动作用下的87.90 cm、1.07 m/s2和157.16 MN·m，分别增大了88.01%、207.48%和40.56%。以上分析表明，脉冲型地震动会增大两种运行状态下风机的塔顶位移、塔顶加速度和泥线处弯矩。其中，塔顶位移和泥线处弯矩的增大可能导致塔架的倾覆破坏，塔顶加速度的增大可能损坏机舱内对加速度较为敏感的电气设备。因此，结构设计时应注意脉冲型地震动对风机结构产生的不利影响。

表4 近场脉冲型地震作用下动力响应最大值

表5 近场非脉冲型地震作用下动力响应最大值

此外，通过表4还发现，在脉冲型地震动作用下，停机状态下风机的动力响应最大值的平均值大于正常运行状态下的风机，塔顶位移、塔顶加速度和泥线处弯矩分别大11.50%、44.68%和8.10%。这一结果说明，在脉冲型地震动作用下，风浪荷载在一定程度上能减轻正常运行状态下风机的动力响应，尤其是塔顶加速度。因此，结构设计时应该更加注意脉冲型地震动对停机状态风机的影响。

5 结 论

通过二次开发建立气动-水动-地震-伺服-土结耦合仿真平台FAST-S，并验证了其可靠性。基于扩展的FAST-S平台，以考虑SSI效应的5 MW近海单桩风机为研究对象，分析了风-浪-地震耦合效应和近场地震动速度脉冲对风机支撑结构动力响应的影响。主要得到以下结论：

(1) 基于FAST仿真平台开发并验证了具有地震载荷分析功能和能够考虑SSI效应的风机耦合仿真软件FAST-S，为海上风机抗震分析提供了有效的工具。

(2) 地震荷载加剧了塔顶振动，使塔顶位移和塔顶加速度增大。风、波浪荷载的存在会增大结构体系阻尼，加速振动能量的耗散，对抑制地震引发的塔顶振动有一定积极作用。

(3) 风机支撑结构最大剪力和弯矩随高度先增大后减小，在泥线以下出现最大值且地震条件下峰值更大，设计时应加强单桩的强度来抵御地震作用。另外，气动载荷、水动载荷和地震载荷之间存在非线性耦合关系，线性叠加会过高估计风机结构受到的载荷，计算时应充分考虑风-浪-地震耦合效应。

(4) 近场地震速度脉冲会增大停机和正常运行状态下风机的塔顶位移、塔顶加速度和泥线处弯矩；脉冲型地震动作用下，风浪荷载在一定程度上可以减轻正常运行风机的动力响应。因此，结构设计时应考虑脉型地震动对风机结构产生的不利影响，特别是停机状态下的风机。