基于特征映射平面的塔机塔身钢结构损伤快速识别方法

杨 蕊, 宋世军, 宋连玉, 安增辉, 臧泓源, 张会敏

(1. 山东建筑大学 机电工程学院， 济南 250101； 2. 山东富友慧明测控设备有限公司， 济南 250101；3. 泰山学院 机械与建筑工程学院， 山东 泰安 271000)

塔机作为一种现代化起重设备在建筑等行业得到广泛的应用。因其常年工作在重载、冲击特性较大的高危场所，在自身重力以及外界复杂环境的影响下，极易发生损伤，带来巨大的经济损失和人员伤亡[1]。而塔身作为主要的承载结构件，是塔机中最容易出现损伤的部位之一[2]。

塔机塔身倒塌事故率高，一旦发生其损伤程度较严重[3]。2019年1月23日华容县华容明珠三期工程项目发生塔机坍塌事故，造成5人死亡，直接经济损伤580余万元。2020年12月8日上午，宁波市杭州湾新区在建工地发生塔吊倒塌事故，事故造成2死1伤。到目前为止，类似事故仍然不断发生。为进一步加强建筑工地安全管理水平，急需一种有效的方法能快速、准确地判别塔机塔身的损伤状态。在其事故发生前就停止其工作，做到“早识别、早监测、早预防、早干预”。

目前起重设备上配置的状态监测系统，实际上是一种安全保护装置，存在着保护装置仅在到达极限状态时才突然产生作用，而在接近极限状态时却仍无法提示的缺点[4]。另外安全保护装置无法完成机械工作过程中有关结构参数的显示，这种设备对于结构状态是否完好，是否存在结构损伤等仍然无能为力。而对于塔式起重机，其金属结构占总机重量的比例可达80%，在起重工作过程中，其钢结构要承受大量的交变载荷作用，而目前对于起重机械钢结构状态监测的研究却鲜有报导。故研究塔机塔身的损伤状态判定方法将进一步推动起重机械钢结构状态监测行业的进一步发展。

对于起重机械钢结构部分的检测，较为先进的监测方法是使用超声波法[5-6]、红外线法、声发射法[7]等技术。但目前我国塔机状态检测方法在许多地方仍然是依靠目测及用手锤检测各连接螺栓是否松动，用力矩扳手抽检螺栓预紧力矩，目测销轴是否用开口销进行轴向制动，开口销是否开口。目测钢结构件有无永久变形、裂纹、损伤、严重锈蚀、焊缝开裂等现象，锈蚀严重处用超声波测厚仪检测其厚度是否超标，对重点易损部位重点检查，定期探伤。即便使用超声波等无损检测技术[8]，检测不但费时，需要昂贵的费用，有些部位还不能检测到，不利于检测建筑工地大型复杂工程的结构损伤，并且不能进行实时监测。此外，这些检测还要求专业人员必须到现场检测。因而这些技术仅能用于建筑工地工程结构的局部损伤检测。

而从识别方法来看：基于固有频率和刚度变化的损伤识别算法不能识别结构的小损伤；基于振型变化的损伤识别算法，为了便于利用中心差分法求取曲率模态，要求测点足够密[9]；基于传递函数变化的损伤识别算法精度受到测量点的数量和位置影响[10-11]；基于神经网络分析[12-13]的结构损伤算法依赖于训练样本的构造，训练样本太少结果不好，太多又很费时；而对于大型钢结构而言基于振动特性的系统损伤识别方法是国内外研究的热点和难题。

为有效地快速识别塔机塔身的损伤状态，本论文将从以下几个方面进行：首先采集塔机塔身不同损伤组合状态下的基础分析数据集；然后对基础分析数据进行归一化处理并进行坐标转换；采用N次和函数进行数据点拟合，并提取特征参数集；构建特征点映射平面，建立损伤状态与单个特征值之间的对应关系，作为塔机塔身状态监测评价参数指标。具体的流程图如图1所示。

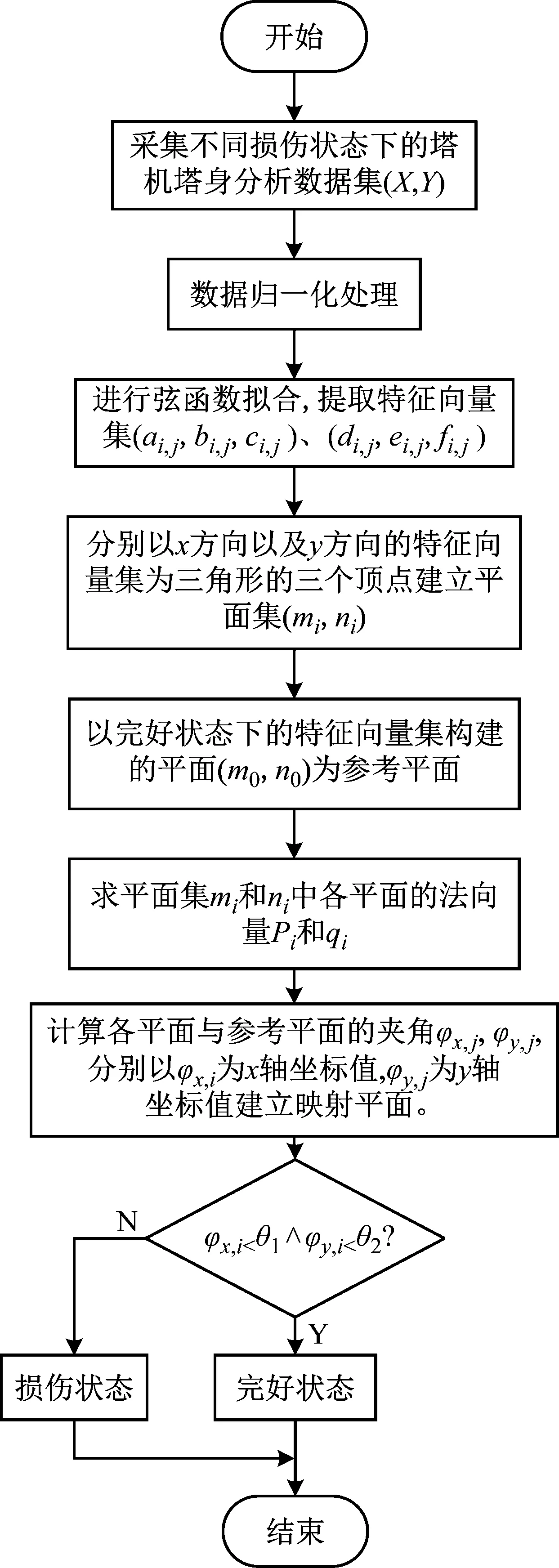
图1 算法的实现流程图

1 理论方法

1.1 基础分析数据的获取

搭建塔机塔身完好状态、单主肢损伤以及同层或不同层多主肢损伤等I+1种不同损伤位置组合状态下的塔机结构。以塔机塔身顶端回转支承回转平面与塔身中心线的交点为坐标原点o，坐标轴x的正方向为沿着起重臂远离塔身方向，z轴正方向是沿着垂直于地面的塔身中心线方向向上，y方向垂直于起重臂轴线方向且和x轴以及z轴符合右手螺旋法则，建立相对坐标系。让回转臂在恒定载荷工况下绕塔机塔身在地面固定截面的中心点垂直于地面的方向且在塔身I+1种损伤状态下都旋转一周，每旋转ω°采集一个相对坐标系的塔机塔身顶端空间位置点集(xi,w，yi,w)，其中w=1,2，…，W(W=360/ω)，i=0，1，…，I。获取I+1种状态下的数据样本集(X,Y)。

X=[X0;X1;X2;…;XI]=

(1)

Y=[Y0;Y1;Y2;…;YI]=

(2)

1.2 提取不同损伤状态下的特征向量集

首先对I+1种不同损伤状态下的塔机塔身顶端空间位置数据点集进行(0，1)标准化处理，然后进行3个正弦和函数拟合，如式(3)和(4)所示

(3)

(4)

式中，j=0,1,2表示拟合得到的正弦函数的个数。ai,j和di,j、bi,j和ei,j、ci,j和fi,j分别表示第i种损伤状态下塔机塔身顶端在x和y方向空间位置点集拟合得到的第j个弦函数的幅值、频率和相位。分别以ai,j，di,j，bi,j，ei,j，ci,j，fi,j作为塔机塔身顶端空间位置点的特征向量集。

1.3 损伤状态特征平面的构建

选取拟合得到的特征向量集构建特征映射平面。以I+1种状态下塔机塔身顶端在x方向的空间位置量的3组特征向量集(ai,0,ai,1,ai,2)、(bi,0,bi,1,bi,2)、(ci,0,ci,1,ci,2)为三角形三个顶点建立平面集mi，以I+1种损伤状态下塔机塔身顶端在y方向的位移量的前3组特征向量集(di,0,di,1,di,2)、(ei,0,ei,1,ei,2)、(fi,0,fi,1,fi,2)为三角形三个顶点建立平面集ni。具体的平面构建方法为：在空间中建立一个三维坐标系OXYZ，分别以ai,0,ai,1,ai,2点值作为X轴、Y轴、Z轴方向上的坐标值，并以此作为三角形的一个顶点，以同样方法寻找坐标为(bi,0,bi,1,bi,2)和(ci,0,ci,1,ci,2)的另外两个点作为三角形的其他两个顶点，三点进行两两连接来构建三角形建立特征平面。y方向的塔机塔身顶端位移量的特征平面以同样的方法进行构建。mi和ni(i=0,2,…，I)表示I+1种状态下的塔机塔身在x方向以及y方向的空间位置数据特征集构建的平面集。

分别求平面集mi和ni中的每个平面的法向量集。

令

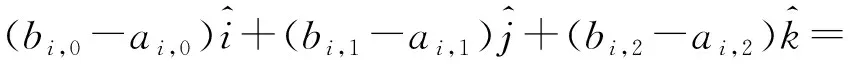
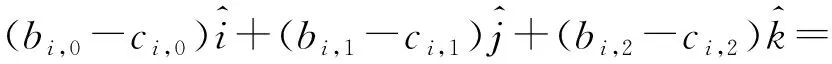
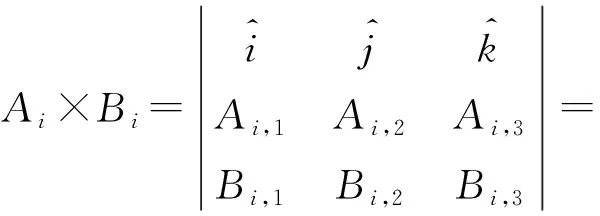
(5)

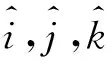
令

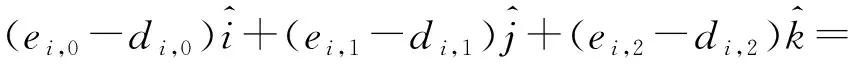
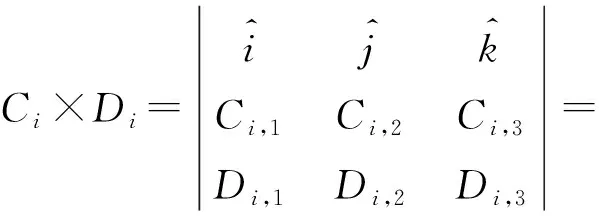
(6)

其中：

Ci=(Ci,1,Ci,2,Ci,3);Ci,1=ei,0-di,0;Ci,2=ei,1-di,1;Ci,3=ei,2-di,2;Di= (Di,1,Di,2,Di,3);Di,1=ei,0-fi,0;Di,2=ei,1-fi,1;Di,3=ei,2-fi,2;Qi= (Qi,1,Qi,2,Qi,3);Qi,1=Ci,2Di,3-Ci,3Di,2;Qi,2=Ci,3Di,1-Ci,1Di,3;Qi,3=Ci,1Di,2-Ci,2Di,1;Qi表示平面集中ni平面对应的法向量集。

将塔机塔身完好状态下的特征向量集构建的平面标记为m0和n0，并将其作为参考平面。分别计算平面集mi(i=1,2,…I)中每个平面与参考平面m0的夹角以及平面集ni(i=1,2,…，I)中每个平面与参考平面n0的夹角。

(7)

(8)

φx,i=arccos(φx,i)

(9)

φy,i=arccos(φy,i)

(10)

式中：φx,i表示平面集mi(i=1,2,…，I)中每个平面与参考平面m0的夹角；φy,i表示平面集ni(i=1,2,…，I)中每个平面与参考平面n0的夹角。

以平面上的一固定点作为坐标原点，过坐标原点且沿着水平方向做一条直线作为x′轴，取向右为正方向，过坐标原点且垂直于x′轴做一条直线作为y′轴，取向上为正方向，建立坐标系o′x′y′。分别以夹角φx,i为x′轴坐标值以及φy,i为y′轴坐标值建立I种状态的特征在二维平面内的映射点云图，将高维数据映射到低维平面单点特征。

1.4 塔机塔身损伤与否的判断依据

依据计算得到的I种状态在x′轴和y′轴方向上的特征平面与参考平面的夹角值φx,i和φy,i来判定塔机塔身损伤状态。当计算所得到的x方向和y方向的平面夹角均小于某个阈值时，认为塔机塔身是完好的；否则，认为塔机塔身处于损伤状态，如式(11)所示。其中阈值θ1，θ2的取值大小主要依据塔机出厂时的状态和主要技术全参数，可以通过计算塔机出厂时在空载和额载状态下的最大特征映射坐标值来获取，也可以根据实际精度需求进行自我调整。

(11)

2 模型分析与算法验证

本实例以QTZ40塔机设计参数为基础，对塔机进行建模分析[14]。整个塔机模型由回转台、塔帽、起重臂和平衡臂、塔身标准节组成，如图2所示。ADAMS模型构建时利用的是符合实际应力测试要求的ANSYS 模型得到的单元质量、转动惯量等参数，将两个标准节做成一个刚体单元，单元之间由八个弹簧连接。沿塔身方向为Z′，Z′方向设置4个弹簧，X′和Y′方向各两个弹簧，如图3所示。而后，对相同外力下 ADAMS模型与 ANSYS 模型的塔帽、回转塔身、起重臂的变形情况进行了比较，ADAMS 模型的变形量与 ANSYS 模型的变形量基本一致，从而验证了ADAMS模型各弹簧刚度的正确性以及整机模型的有效性[15]。

相对于标准节本体而言，塔身两标准节螺栓连接处位置是最广泛的塔身损伤状态，故本文针对于标准节螺栓连接位置损伤类型进行了分析并对算法进行了验证。本实例中建立的模型为刚体结构，刚体结构在外力的作用下不会发生变形。为了尽可能准确、全面的获取塔身标准节螺栓连接部位的不同损伤量，在保持塔机ADAMS模型其他结构完好的前提下，通过调整塔身模型中标准节之间沿Y方向的连接弹簧的刚度来改变损伤量对塔机塔身损伤状态进行模拟，在本文中调整弹簧刚度为k/2(k为弹簧的刚度系数)得到塔身不同状态下的塔身的变形量和顶端位移量。搭建塔身主肢完好状态、单主肢损伤以及同层或不同层多主肢损伤等31种不同损伤位置组合状态下的塔机结构，通过测量塔身顶端在相对坐标系中到原点的位移量来获取基础分析数据集。表1给出了塔机塔身损伤位置组合状态图，图中左侧0～30是损伤状态标号，图中一、二、三、四、五表示塔机塔身标准节的层数，横向数字1～4表示每层标准节上的主肢按照逆时针进行的编号，“√”表示所对应主肢发生了损伤。

图2 塔机整机模型图

图3 塔机局部结构放大图

使塔机模型在31种损伤状态下旋转360°，每隔15°采集一个相对坐标系的塔身顶端空间位置点集。按照所提方法首先将获取的基础分析数据进行3个弦函数和拟合，提取其特征参数集，然后采用特征参数集构建平面，得到一系列的平面集，如图4所示。在图4中simx(i=0,1,2,…,30)表示x方向的塔机塔身顶端位移量的特征平面，siny(i=0,1,2,…,30)表示y方向的塔机塔身顶端位移量的特征平面，s0mx和s0ny为参考平面。图5(a)、(b)、(c)、(d)分别为i=1,2,3,4的四种损伤状态与参考平面的关系图的示意图。计算同一型号塔机塔身各损伤状态下的特征集平面与完好状态特征映射参考平面之间的夹角的关系，并将结果进行平面可视化处理，如图5所示。

表1 塔机塔身损伤位置组合状态描述

在图5中，横轴表示塔机塔身顶端空间位置坐标在x轴方向的数据集的特征构建的平面与参考平面的夹角值，纵轴表示塔机塔身顶端空间位置坐标在y轴方向的数据集的特征构建的平面与参考平面的夹角值。从图中可以看出，塔机塔身在各损伤状态下的平面与参考平面的夹角φx,i≥θ1,φy,i≥θ2, 各角度在特征映射平面内都分布在安全区域外围，可以判定塔机塔身在表1中标号为1～30的工况下都发生了损伤，此结果与实际情况相符。

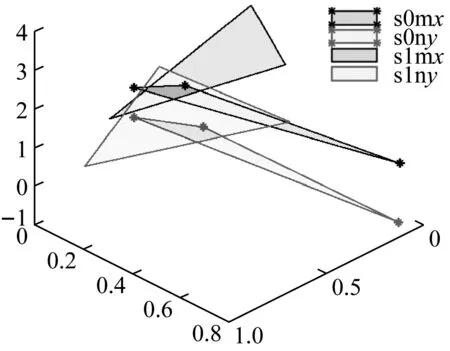
(a)

图5 特征映射平面点云图

3 试验数据分析与算法验证

考虑利用真实塔机获取塔身损伤状态下的顶端轨迹危险性极高，为进一步验证本文所提算法有效性，搭建了物理试验台进行算法验证。对QTZ40塔机的实际参数进行22倍缩小，并对其结构进行了简化，搭建了塔机结构物理试验台，模拟塔机塔身结构损伤状态并获取基础分析数据集，如图6、图7所示。其中，底架对应塔机基础；四根圆形钢管对应塔身标准节；圆钢管之间的连接板、弹簧和螺栓模拟标准节之间的连接；装置前臂对应塔机起重臂；装置后臂对应平衡臂；重物块对应塔机平衡重。在采集过程中，状态数据采集装置安装在塔机回转支承以上的回转部分，保证其采集的顶端位移为塔机相对坐标系中的信息。图8给出了数据采集仪器外观图，具体安装方式请见图6中物理模型顶端红色虚线框位置。

图6 塔身结构损伤模拟试验台物理图

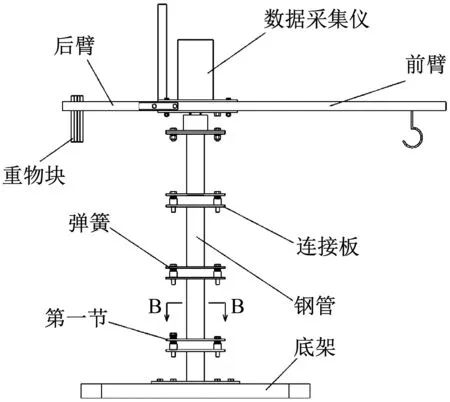
(a) 整体结构简图

采用上述物理试验台分别模拟塔机塔身不同损伤位置状态。调整1/2/3/4号主肢处弹簧压缩量分别模拟单主肢损伤;同时调整1号和2号主肢处弹簧压缩量模拟同一层相邻主肢损伤;同时调整1号和3号主肢弹簧压缩量模拟同一层相对主肢损伤。损伤量设定为50%，也即弹簧刚度为k/2，读取不同损伤状态下的顶端轨迹数据，并采用本文所提方法对物理模拟试验台的塔机运行状态数据进行分析得到特征映射平面图，如图9所示。

图8 数据采集仪器外观图

从图9可以看出，塔机塔身在无损伤的状态下，其特征映射点位于离原点较近的区域内，也即安全区域内。当塔身发生损伤时，其特征映射点会发生偏移，远离原点位置。采用本文所提方法对物理模拟试验台获取的几种损伤数据进行分析，可以看到其特征平面内的点位于远离原点的区域，也即安全区域之外。综上所述，本文所提算法在塔机塔身结构损伤快速判别方向是有效性。

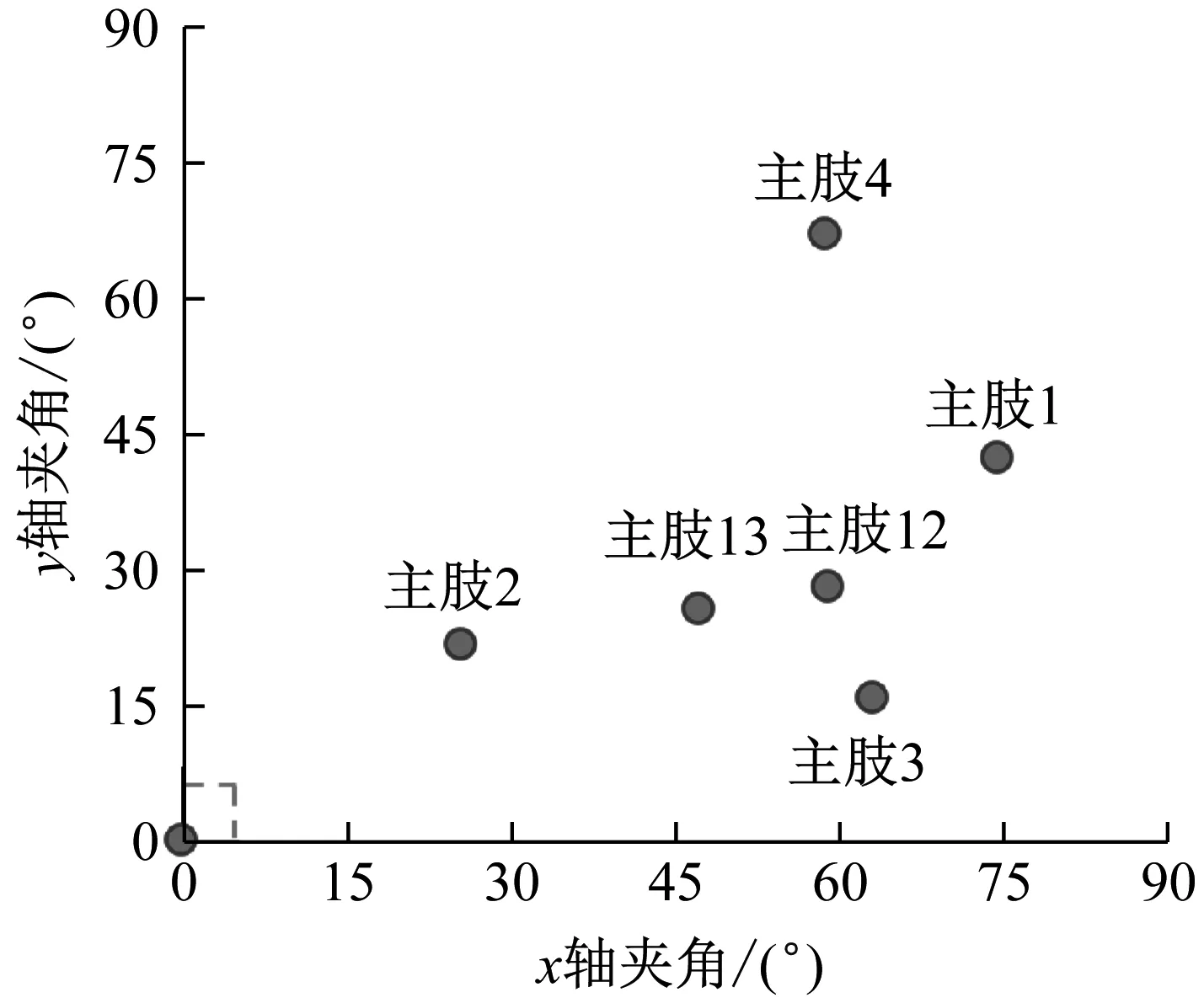
图9 物理模拟试验台塔机状态数据特征映射平面图

4 结 论

针对塔机的主要承载结构件塔身易损伤且缺乏一种对其进行快速、有效且准确的识别方法问题，以塔身顶端在x轴和y轴方向的空间位置坐标值作为基础分析数据，采用3个弦函数和进行参数化拟合并提取参数特征集，通过构建特征集平面并计算平面与完好状态下的参考平面的夹角，以各夹角数值作为损伤状态评判依据，进一步将夹角值转化成平面点云图进行可视化处理，通过点的分布区域能对塔机塔身的运行状态进行快速、准确地识别。为验证所提方法的有效性，对QTZ40塔机实体模型数据进行了分析，结果表明该算法可以通过构建得到的塔机塔身状态数据特征映射平面来实现数据降维，并依据平面内特征点的分布区域快速识别塔机的损伤状态。