基于RBF神经网络的Bootstrap数据扩充方法及其在IRSS可靠性估计中的应用
汤少敏, 刘桂雄, 李小兵
(1. 华南理工大学机械与汽车工程学院,广东 广州 510640; 2. 工业和信息化部第五研究所,广东 广州 510610)
0 引 言
对于高可靠性、长寿命机械部件,其可靠性试验常常面临测试子样少、测试时间有限等问题,导致可靠性试验数据样本较少而难以进行有效可靠性评估[1-2]。针对小样本可靠性评估问题,Bootstrap法[3]通过重复抽样扩充可靠性试验数据,无需预设样本分布,获得广泛应用。文献[4]应用Bootstrap方法扩充样本估计卫星空间用导电滑环寿命分布参数,最后结合传统可靠性预测方法,得到滑环一系列可靠性指标。文献[5]结合Bootstrap自助法扩充轴承性能退化试验数据,再根据基于退化轨迹的信息补充方法进行其可靠性评估。
经典Bootstrap法基于原样本经验分布,当原样本容量较小时,原样本经验分布特征不显著,加之扩充样本取值范围局限于原样本,无法有效利用原样本上、下限数据信息,容易导致扩充样本分布一定程度偏离原样本真实分布。为此,本文从原样本经验分布出发,借助径向基函数(radial basis function, RBF)神经网络拟合原样本经验分布,获取原样本连续分布特性,并利用邻域抽样方法构造RBF神经网络输入集,从而获得更接近于原样本真实分布的扩充样本。
1 基于RBF神经网络的Bootstrap数据扩充方法
图1为基于RBF神经网络的Bootstrap数据扩充方法流程图,获取原样本集合X={x1, x2, ···, xn}的经验分布值集合F={Fn(x1), Fn(x2), · ··, Fn(xn)};基于原样本集合X与经验分布值集合F训练RBF神经网络;由于RBF神经网络对靠近其训练样本的输入有更可靠输出[6],这里通过构建F的邻域函数Ri,构造RBF神经网络输入集Sin,输入训练好的RBF神经网络,获得扩充样本集合X*。具体实施步骤为:

图1 基于RBF神经网络的Bootstrap数据扩充方法流程图
1)获得原样本集合X的经验分布值。X={x1,x2, ···, xn}元素按从小到大排列得到其次序统计量集 X'={x(1),x(2), ···, x(n)} (其 中 x(1)≤ x(2)≤ ···≤x(n)),构造X的经验分布分布函数Fn(x):

将X元素代入上式,即得到X的经验分布值集合F={Fn(x1), Fn(x2), · ··, Fn(xn)}。
2)训练RBF神经网络。以X的经验分布值Fn(x(i))(i∈[1, n])作为 RBF 神经网络输入 sj,x(i)作为网络输出oj,训练RBF神经网络,网络选用高斯型径向基函数[7]:
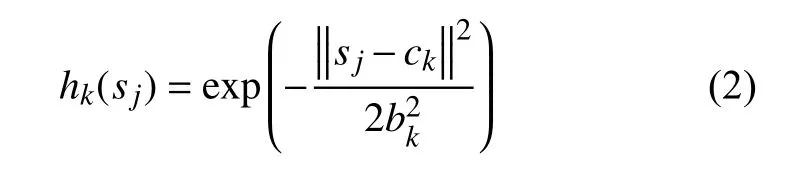
式中:ck——核函数中心,采用无监督k-means训练算法确定;
bk——高斯函数半径,用正交最小二乘法训练算法确定。
3)构建X的经验分布值集合F邻域函数Ri,获得RBF神经网络输入集Sin。令fi= Fn(x(i)),那么Fn(x(i))的邻域函数Ri为:
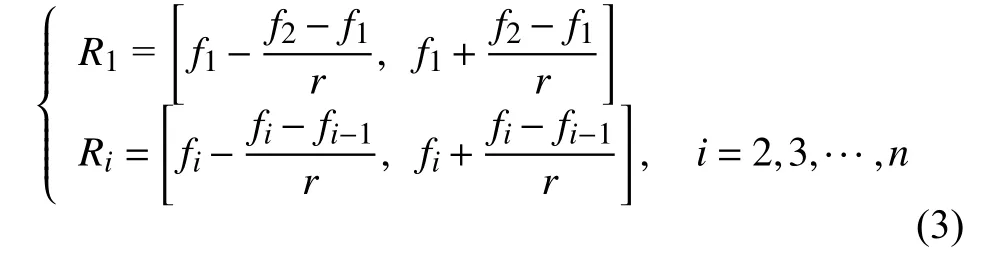
其中r为取邻域参数,r≥2。按顺序i=1,2, ···,n从各邻域Ri的均匀分布U[Ri]产生RBF神经网络输入集 Sin,有 Sin={s1, s2, ···, sj, ···, sn},其中 sj~ U[Rj]。
4)将输入集Sin输入RBF神经网络,获得扩充样本X*。将Sin中元素逐一输入RBF神经网络,设RBF神经网络输入为sj,其输出oj为:

由RBF神经网络输出oj组成的集合即为X的扩充样本X*。
5)按重复抽样次数N重复步骤3)、4),得到X的扩充样本X*(k) ={xk1*, xk2*, ···, xkn*}(k=1, 2 , ···, N)。
2 仿真分析
设原样本集合X={x1, x2, ···, x30}为卡方分布χ2(5)独立随机样本,样本容量n=30,样本取值区间VI=[0.693 2, 13.472 5],将X扩充为样本容量N=300的扩充样本X*。分别用经典Bootstrap法、基于RBF神经网络的Bootstrap数据扩充方法(下简称“RBF+Bootstrap法”)获得扩充样本X*,表1为扩充样本X*的分布特性表。

表1 扩充样本分布特性表
可以看出:
1)由χ2(5)分布产生数据、Bootstrap法扩充样本、“RBF神经网络+Bootstrap法”扩充样本X*期望值及95%置信区间长度分别为E=5.000 0,5.231 2,5.059 5和 L=0.699 0,0.776 6,0.687 1。“RBF 神经网络+Bootstrap法”与由 χ2(5)本身的期望值E、95%置信区间长度 L的差值分别为 0.059 5、0.011 9,小于Bootstrap 法的相应差值 0.231 2、0.077 6,因此“RBF神经网络+Bootstrap法”扩充样本X*分布特性更接近于原样本X的真实 χ2(5)分布。
2)由 χ2(5)分布产生数据的取值区间、Bootstrap法扩充样本 X*的取值区间、“RBF神经网络+Bootstrap法”扩充样本X*的取值区间分别为VI=[0.049 7, 19.444 4]、 [0.694 9, 13.352 9]、 [0.044 5,13.472 5]。Bootstrap法扩充样本 X*的取值区间[0.694 9, 13.352 9]局限于 X的 [0.693 2, 13.472 5],“RBF神经网络+Bootstrap法”取值区间VI [0.044 5,13.472 5],拓展了原样本下限,但未拓展原样本上限,这是由于原样本数据上限13.472 5附近数据稀少,RBF神经网络训练不足造成的。但“RBF神经网络+Bootstrap法”扩展数据下限仍大于Bootstrap法的。因此,“RBF神经网络+Bootstrap法”有效利用了原样本取值区间上、下限数据信息,一定程度改善了经典Bootstrap法取值区间局限于原样本问题。
3 在IRSS可靠性评估中的应用
工业机器人伺服系统(industrial robot servo system, IRSS)是用于完成工业机器人特定轨迹运动的执行单元,是工业机器人核心部件,其可靠性直接关系工业机器人正常使用寿命[8]。IRSS系典型长寿命、高可靠产品,其可靠性评估面临测试子样少、试验时间有限导致的可靠性试验数据不足问题。
基于伪失效寿命分布拟合的可靠性评估方法,是分析长寿命、高可靠性产品性能退化可靠性的有效方法[9]。图2为IRSS伪失效寿命分布拟合可靠性评估方法流程图,基于IRSS性能退化数据,通过设置伪失效水平,获取IRSS伪失效寿命数据集,建立各伪失效水平IRSS伪失效寿命分布,最后外推失效阈值下寿命分布,完成可靠性评估。

图2 IRSS伪失效寿命分布拟合可靠性评估方法流程图
表2为基于IRSS性能退化数据获得的某型号IRSS 伪失效寿命数据表,设置 w1、w2、w3、w4、w5、w6、w7等7个伪失效水平,IRSS试验子样5件,每个伪失效水平获得5个IRSS伪失效寿命数据。IRSS可靠性试验子样少,导致其伪失效寿命数据容量较小,为IRSS伪失效寿命分布建模带来困难,这里应用基于RBF神经网络的Bootstrap数据扩充方法扩充IRSS伪失效寿命数据,开展IRSS可靠性评估。

表2 IRSS伪失效寿命数据表 h
图3~图 9 为 w1、w2、w3、w4、w5、w6、w77 个伪失效水平的IRSS伪失效扩充数据直方图及伪失效寿命分布估计结果。基于各失效水平伪失效寿命分布估计结果,外推失效阈值wth下IRSS寿命分布f(t,wth),图10(a)、(b)分别为其寿命分布概率密度函数图、失效分布图。其中,IRSS失效寿命估计值Tfailure=11 264.75 h,与厂商提供的该型号IRSS额定寿命值10 000 h相近。

图3 w1下寿命分布
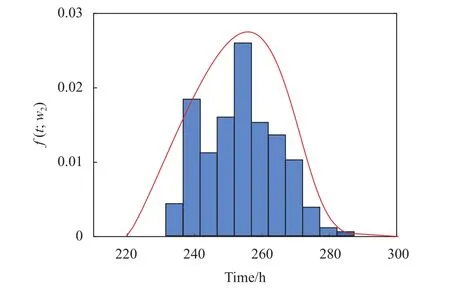
图4 w2下寿命分布

图5 w3下寿命分布

图6 w4下寿命分布

图7 w5下寿命分布

图8 w6下寿命分布

图9 w7下寿命分布
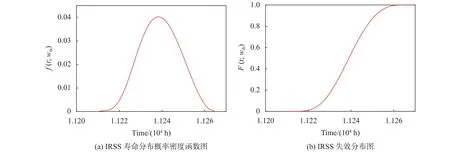
图10 IRSS可靠性评估结果图
表3对比了不同方法获得的本文IRSS可靠性评估结果。由经典退化轨迹法获得的IRSS失效寿命估计结果为13 269.90 h,与额定值10 000 h相比,相对误差32.70%;由本文方法(伪失效寿命分布拟合+基于RBF神经网络的Bootstrap数据扩充方法)获得可靠性评估结果为11 264.75 h,与额定值的相对误差12.65%;本文方法评估结果与IRSS额定寿命更接近,相对误差减小61.32%,证明了本文可靠性评估方法有效性。另外,表中列出同样基于伪失效寿命分布拟合方法进行IRSS可靠性评估,采用经典Bootstrap法扩充伪失效数据,得到的IRSS失效寿命估计值为12 012.25 h,相对误差20.12%,对比采用本文数据扩充方法评估结果相对误差增大37.13%,表明采用本文基于 RBF神经网络的Bootstrap数据扩充方法扩充伪失效数据,更有助于获取伪失效水平下真实寿命分布,进而实现IRSS可靠性有效评估。

表3 不同方法的IRSS可靠性评估结果对比
4 结束语
1)经典Bootstrap法基于原样本经验分布,当原样本容量较小时,容易导致扩充样本分布一定程度偏离原样本真实分布,且无法有效利用原样本上、下限数据信息。本文提出基于RBF神经网络的Bootstrap数据扩充方法,借助RBF神经网络获取原样本连续分布特性,并利用邻域抽样方法构造网络输入集。仿真表明由基于RBF神经网络的Bootstrap数据扩充方法获得的扩充样本分布特性更接近于原样本的真实分布,并有效利用了原样本取值区间上、下限数据信息,改善经典Bootstrap法扩充样本取值区间局限于原样本问题。
2)将基于RBF神经网络的Bootstrap数据扩充方法应用于工业机器人伺服系统IRSS伪失效寿命分布可靠性评估,扩充IRSS伪失效寿命数据,便于其中各失效水平IRSS伪失效数据寿命分布建模。最终外推失效阈值wth下IRSS失效寿命估计值Tfailure=11 264.75 h,对比厂商提供的该型号IRSS额定寿命10 000 h,相对误差12.65%,与采用经典Bootstrap法扩充伪失效数据样本获得的可靠性评估结果相比,相对误差减少37.13%,表明了采用基于RBF神经网络的Bootstrap数据扩充方法扩充伪失效数据,更有助于获取伪失效水平下真实寿命分布,进而实现IRSS可靠性有效评估,方法具实际应用价值。

