磁流变弹性体宽频负相关特性试验研究

杨明亮， 王 凯， 王秀鹏， 杨勇彬， 吴昱东， 胡志锐， 丁渭平

(1. 西南交通大学机械工程学院，四川 成都 610031; 2. 先进驱动节能技术教育部工程研究中心，四川 成都 610031;3. 中国核动力研究设计院设计所，四川 成都 610213; 4. 西南交通大学轨道交通国家实验室（筹），四川 成都 610031)

0 引 言

磁流变弹性体（magneto-rheological elastomer,MRE）是在磁流变液（magneto-rheological fluid,MRF）的基础上发展而来的一种复合智能材料，它克服了MRF易沉降、稳定性差、颗粒易磨损等缺点，通过施加外部磁场对其力学性能进行快速、低能耗且可逆的控制[1-3]。基于此，将MRE作为传统被动控制元件的理想替代装置并用于在工程结构减振降噪以及车辆噪声、振动及其舒适性（noise vibration &harshness, NVΗ）控制领域得到了深入的研究[4-5]。

MRE由Rigbi[6]等人通过在弹性基体里面加软磁铁颗粒制备而得，随后Jolly[7]等人提出了准静态磁偶极子模型，从理论上推导出MRE在磁场条件下磁致模量的表达式，并用试验进行了验证。随后MRE磁致剪切性能、磁致压缩性能、磁致变形、电学性能以及抗疲劳老化等性能得到了广泛而深入的研究[8-9]。由于MRE磁致压缩性能在抗大变形和承载力方面具有明显的优势，引起了研究者的高度关注，并从理论、试验以及工程应用方面开展了大量的研究工作[10-11]，为MRE在更加广阔的领域进行应用奠定了理论和应用基础。然而，关于MRE磁致压缩性能的研究大多只关注了MRE磁致压缩静态或准静态性能，在实际应用中尤其是振动控制领域，往往需要考虑其动态性能的变化，分析并匹配MRE系统以评估能否达到控制效果，可见掌握MRE磁致压缩动态性能的重要性。而MRE磁致压缩动态性能随外界条件改变是如何变化的，影响因素是什么，有何规律，目前尚未见到系统而全面的研究报道。

本文在综合分析MRE磁致压缩性能研究进展基础上[12]，开展了影响MRE磁致压缩性能的理论分析，确定了影响MRE磁致压缩性能的主要因素，并从试验研究的角度去探明MRE磁致压缩动态性能影响规律，为MRE更加广阔的工程应用提供理论依据和指导。

1 MRE磁致压缩性能理论基础

MRE磁致力学性能（含磁致压缩性能）理论研究大多基于磁偶极子模型及其修正模型，当磁性颗粒固定在基体中，受到拉压变形时以及磁场作用下，由磁性颗粒形成的磁链也将发生变形（常将磁链变形分为纯弯曲和拉长弯曲两种），相邻颗粒之间必将产生拉压力，进而改变磁致压缩性能[13]。本节关于MRE磁致压缩性能理论介绍目的在于分析并确定影响MRE磁致压缩力的因素，为开展MRE动态性能试验方案设计提供理论依据，故在此直接引用了MRE磁致压缩力的理论表达式，省略了其详细推导过程，详见文献[13]。

在纯弯曲变形的条件下，MRE的压缩力与压缩应变关系如图1所示。图中，H为外加磁感应强度；、为相邻颗粒各自中心点；为颗粒连心线与磁场方向的夹角；相邻颗粒磁场综合力；为相邻颗粒磁场综合力沿颗粒连心线方向分力；为相邻颗粒磁场综合力切向分力；R为颗粒链曲率半径；为磁链包角；为颗粒间的平衡力矩；为磁致压缩力。

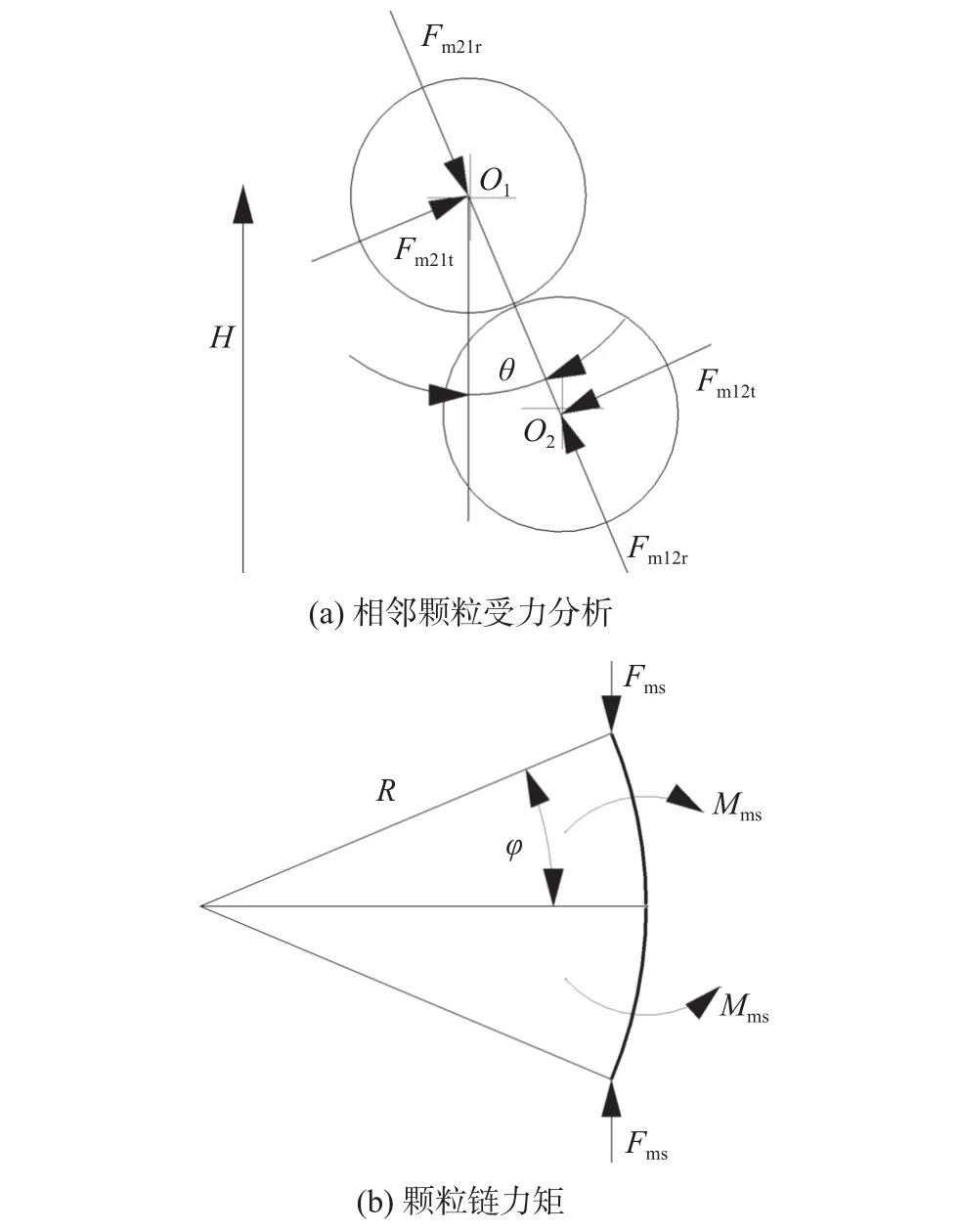
图1 纯弯曲变形条件MRE压缩力与压缩应变关系

磁场力引起的MRE磁致压缩力变化关系如下式所示。

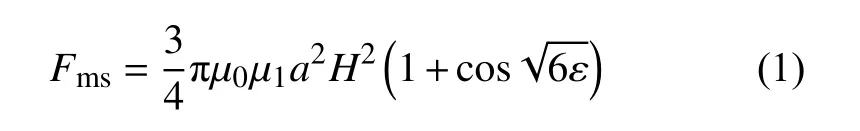
a——磁性颗粒半径；

在拉长弯曲变形条件下，磁性颗粒之间的间距增大，在外加磁场作用下，相邻颗粒之间的引力会对MRE内部进行径向挤压。MRE的压缩力与压缩应变关系如图2所示。图中，为第i个颗粒在弯曲方向的分力；为颗粒链的弯曲程度（角度）；S为相邻磁性颗粒间距，可近似认为S=2a；为颗粒链上的分布力；和分别是在颗粒链上积分的挤压合力在z和r方向上的分量；为MRE受到的压缩力。

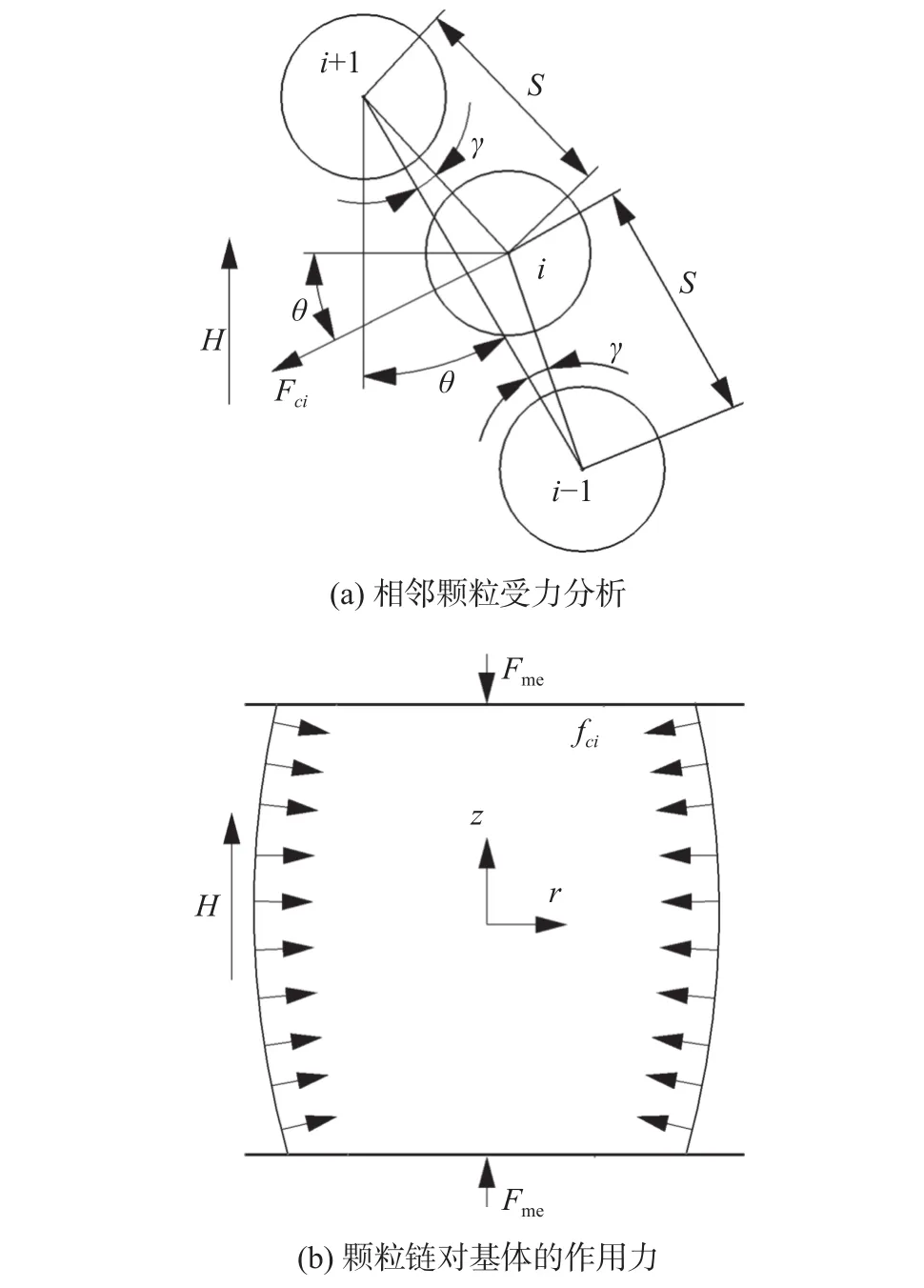
图2 拉长弯曲变形条件下MRE压缩力与压缩应变关系

磁场力引起的MRE磁致压缩力变化关系如以下公式所示。

综合分析式（1）～式（3）关于MRE拉压变形时磁致压缩力的理论推导结果发现：在磁场的作用下，纯弯曲变形和拉长弯曲变形都将引起磁致压缩力增大。从微观层面分析，压缩力增大会使MRE弹性模量、应变等增大；从宏观层面分析，压缩力增大会使MRE刚度、阻尼等增大。同时，基于上述理论推导可知MRE磁致压缩性能（压缩力）主要受MRE基体相对磁导率、磁性颗粒半径（形状）以及外加磁感应强度的影响，且压缩力的大小随着上述三因素的增大而增大，即MRE磁致压缩性能与该三因素呈正相关特性。

2 MRE试验样件与试验系统

2.1 MRE试验样件

MRE主要包括高分子橡胶类基体、磁性颗粒和添加剂三部分。基体方面，为便于比较基体相对磁导率对MRE磁致压缩性能影响，选择天然橡胶（NR）和三元乙丙橡胶（EPDM）两种，相对磁导率EPDM大于NR。磁性颗粒方面，选择羰基铁粉，因其具备高磁导率、高饱和磁化强度以及低剩余磁化强度，可使MRE获得高的磁流变效应和较好的可逆性[14]。为比较粒径对MRE磁致压缩性能影响，根据文献[14]关于“最佳磁致特性与颗粒体积比、磁场强度的关系”研究结论，MRE样件羟基铁粉粒径选择 4 µm，5 µm 和 6.5 µm 三种，在 MRE 中质量分数占比均为65%。添加剂方面，采用硬脂酸和炭黑，用于调节基体粘度，提高基体柔韧性以及减低颗粒在基体中的运动阻力。制备的MRE组合形式如表1所示，试验样件如图3所示。表1中MRE_NR_X和MRE_EPDM_X分别表示不同粒径的NR基体MRE样件和EPDM基体MRE样件，后续相关图、表中的表达方式亦如此。

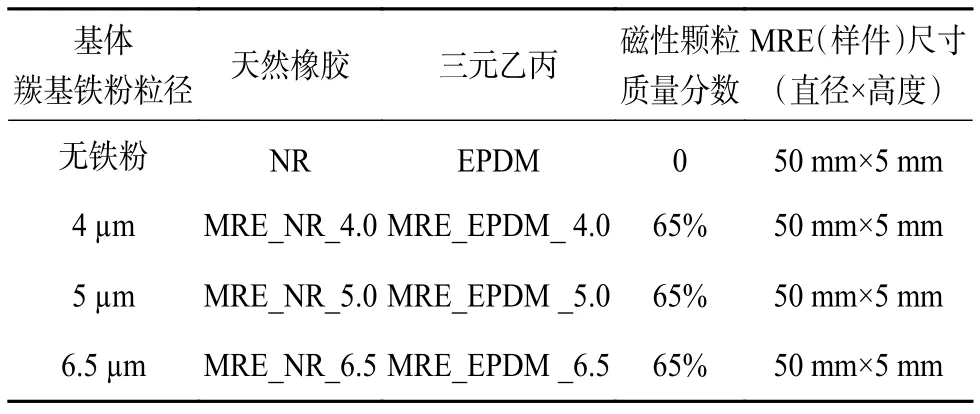
表1 MRE（样件）制备组合

图3 MRE试验样件

2.2 MRE磁致压缩性能试验系统

为准确获取MRE磁致压缩动、静态特性（刚度、阻尼），采用如图4所示试验原理及测试系统。

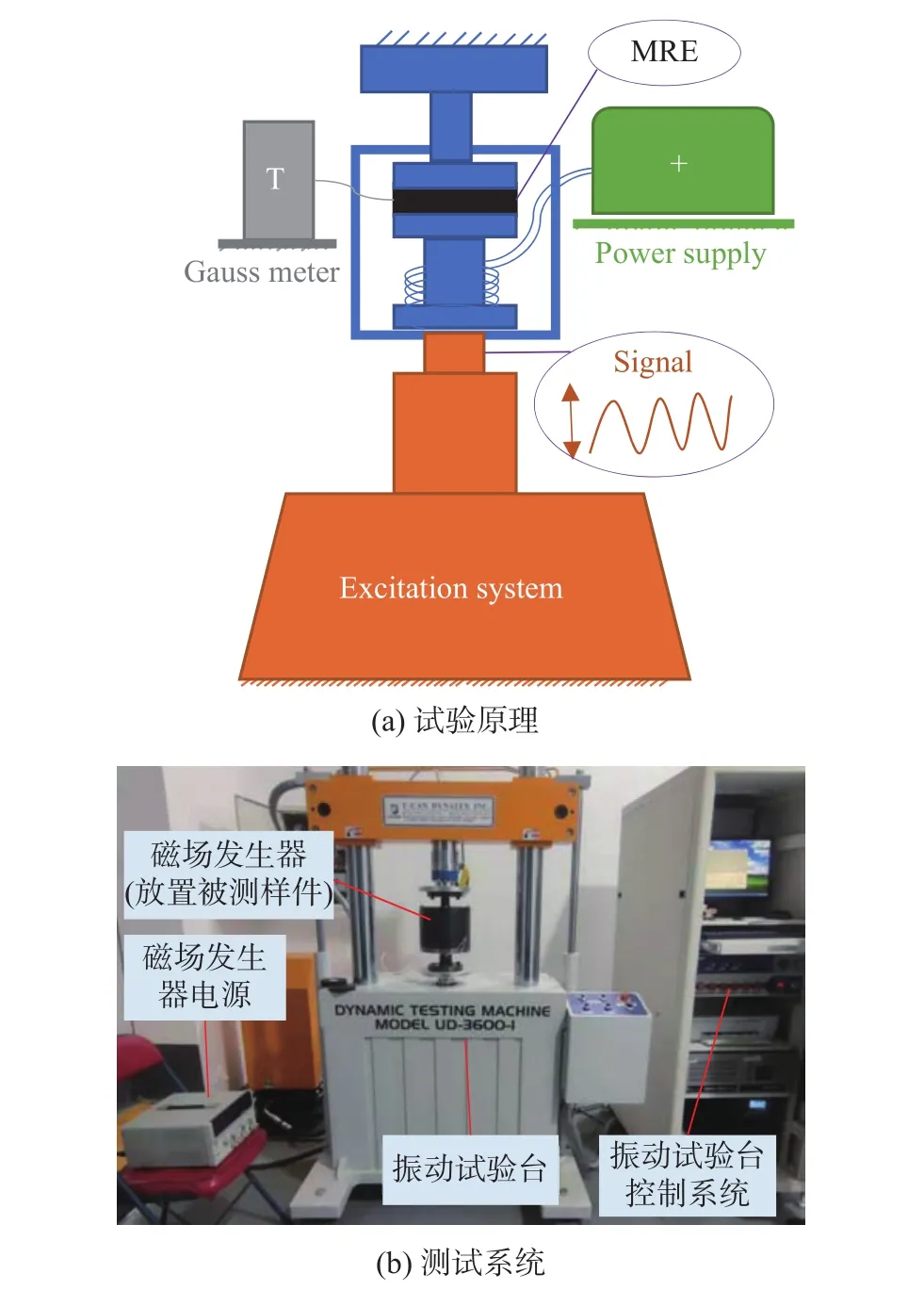
图4 试验原理及测试系统

测试系统中，振动试验台最大加载20 kN，最高测试频率400 Ηz；加载力使用盘式荷重元力传感器测量，误差为±1%，动态力使用动态荷重元力传感器测量，非线性度为±2% F.S.，位移测量使用LVDT位移传感器，行程为±25 mm，非线性度±0.25% F.S.。数据采集系统集成于振动试验台控制系统中，采样频率最高达1 000 Ηz。磁场发生器电源可实现恒流、恒压控制，最大功率2 kW。磁场发生器是产生磁流变特性的关键部件，直接影响MRE外加磁场大小，基于磁感应理论对其进行了详细分析与设计，为使磁场发生器在通入2 A电流情况下产生0.7 T磁感应强度，选用标称直径为0.57 mm，外皮直径为0.62 mm的铜漆包线，计算所需线圈匝数为4 274匝（实际取5 000匝），结构形状参数如图5所示。底座、外筒和顶盖均选用高感磁性、低抗磁性的电工纯铁DT4，箭头方向即为该磁场发生器磁路。

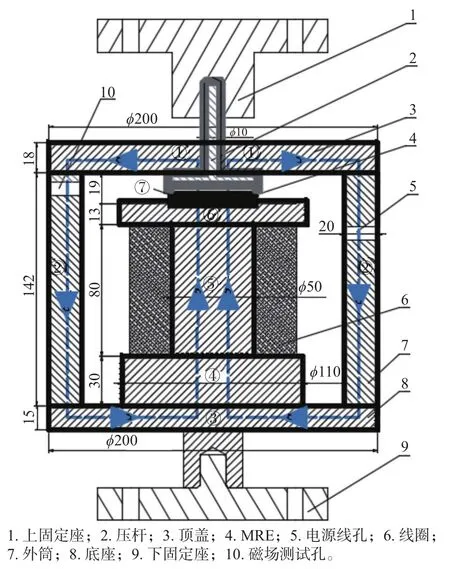
图5 磁场发生器结构（单位：mm）

3 MRE试验方案设计

基于所搭建的试验系统，在不通磁和通磁条件下开展MRE刚度和阻尼随着影响因素改变而变化的试验研究，试验内容和项次如表2所示。表中“是&否”表示通磁与不通磁条件都需要分别进行试验。为排除试验数据的偶然性，每个试验样件同一试验方案做三次试验，要求试验数据接近并对三次数据进行平均处理。如果某一次试验数据存在明显差异，则重新试验，直至符合要求为止。

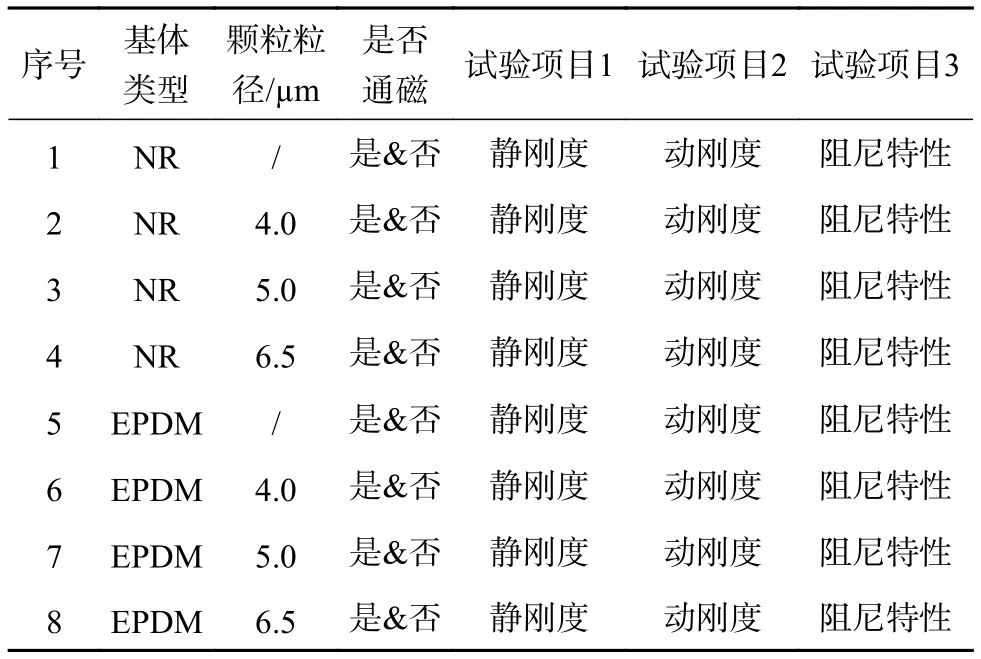
表2 试验内容和项次

4 MRE试验数据分析

4.1 MRE静态性能分析

分别在通磁和不通磁条件下对MRE开展静刚度试验，将被测件置于磁场发生器中，预压1 mm，以0.1 mm/s的速度缓慢压缩，最大压缩变形量2 mm，得到如图6所示曲线。

图6 静刚度测试曲线

静刚度试验表明，MRE磁致压缩静态性能随基体相对磁导率、磁性颗粒粒径以及磁感应强度的增加而增加，MRE_EPDM可调静刚度范围更宽，对磁场变化、磁性颗粒粒径更敏感，规律性更强。进一步说明，对MRE磁致压缩静态性能（静刚度特性）的预测可基于磁偶极子理论构建的MRE磁致压缩性能模型（后简称：磁偶极子模型或模型）。

4.2 MRE动态性能分析

分别在通磁和不通磁条件下对MRE开展动态性能试验（动刚度和阻尼性能试验），将被测件置于磁场发生器中，预压1 mm，振幅±0.025 mm，测试频率0～240 Ηz扫频。将相同粒径不同磁感应强度的MRE动刚度值进行平均得到如图7所示曲线；将相同磁感应强度不同粒径的MRE动刚度值进行平均得到如图8所示曲线；将相同粒径不同磁感应强度的MRE阻尼系数进行平均得到如图9所示曲线；将相同磁感应强度不同粒径的MRE阻尼系数进行平均得到如图10所示曲线。

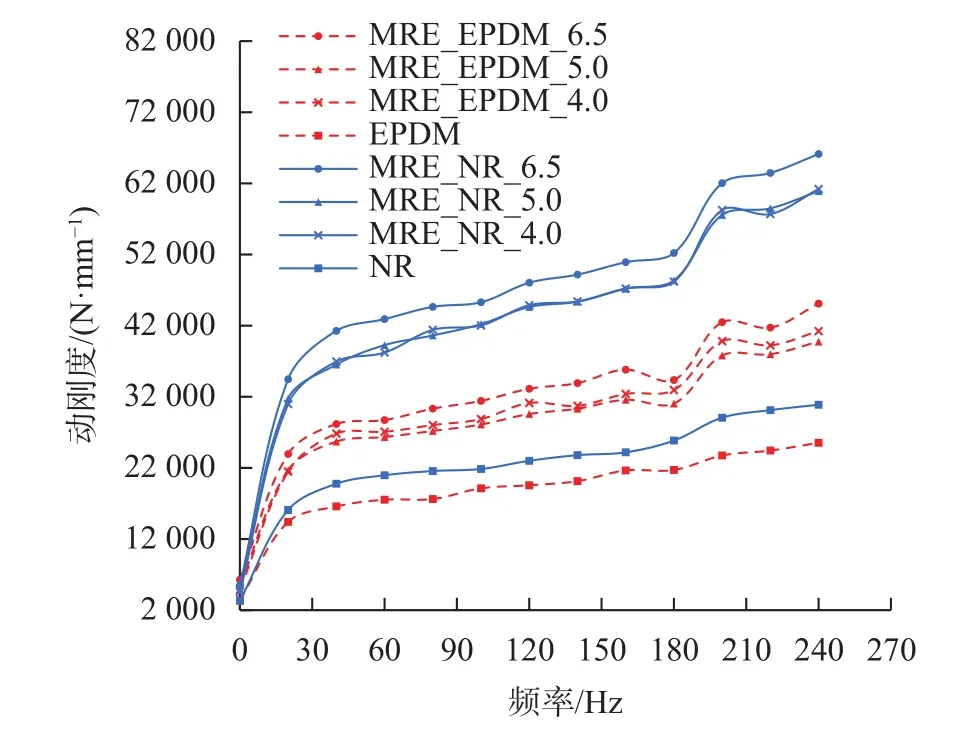
图7 基体相对磁导率及磁性颗粒粒径对MRE动刚度影响

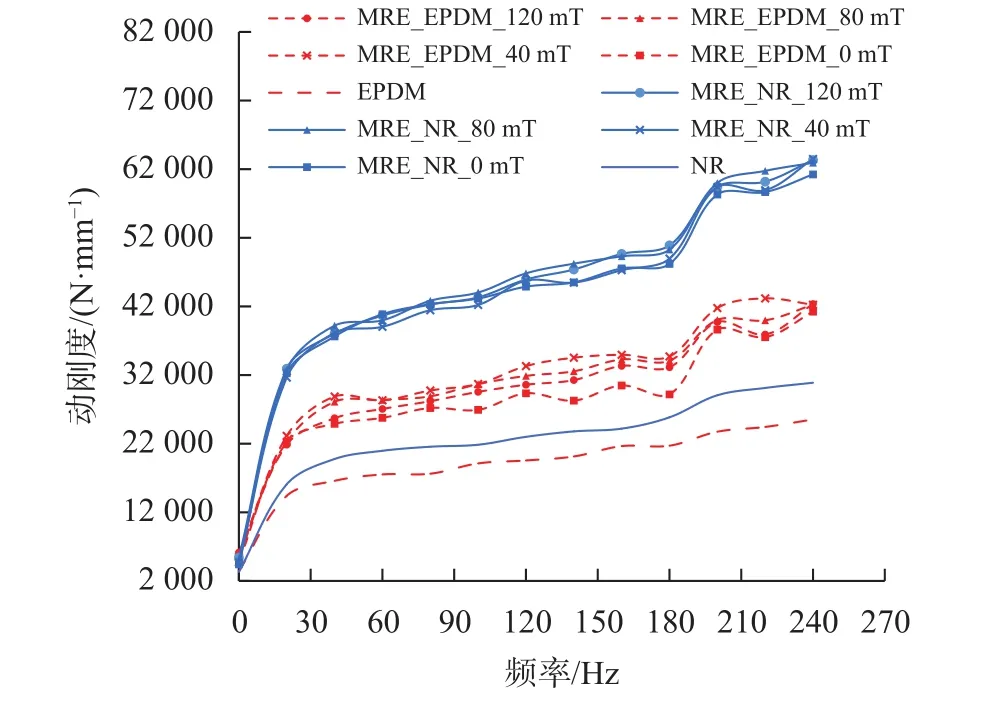
图8 基体相对磁导率及磁感应强度对MRE动刚度影响

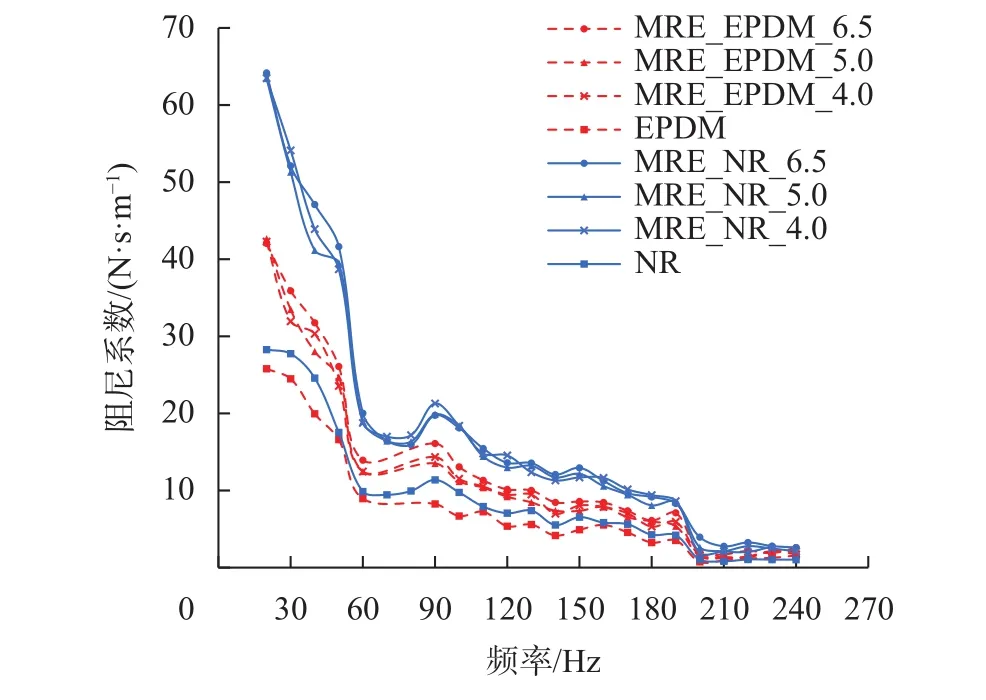
图9 基体相对磁导率及磁性颗粒粒径对MRE阻尼特性影响

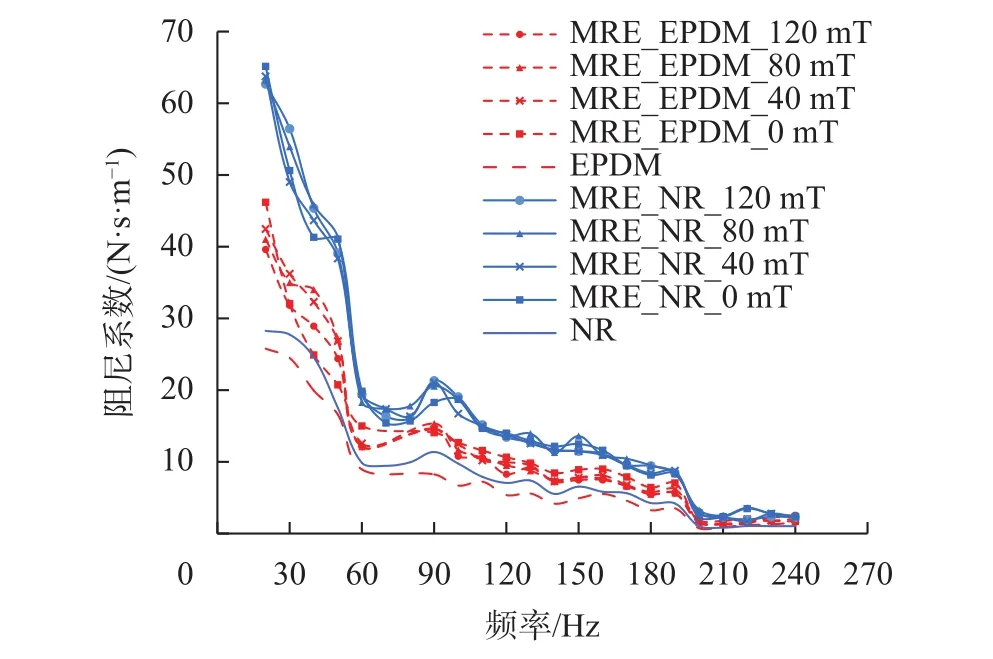
图10 基体相对磁导率及磁感应强度对MRE阻尼特性影响

4.2.1 基体相对磁导率的影响

对图7和图8分析发现，试验频率范围内特别是 20～240 Ηz，MRE_NR 动刚度明显高于 MRE_EPDM动刚度，各频点平均高出47.3%，即基体相对磁导率越大，动刚度越小；对图9和图10分析发现，试验频率（宽频）范围内，MRE_NR阻尼系数明显高于MRE_EPDM阻尼系数，即基体相对磁导率越大，MRE阻尼系数越小，但随着频率增加，两种基体的MRE阻尼系数差异逐步缩小，尤其是高于200 Ηz后，阻尼系数非常接近。试验结果与磁偶极子模型预测结果趋势相反，即基体相对磁导率对MRE磁致压缩阻尼特性在宽频范围内呈现出负相关特性。

4.2.2 磁性颗粒粒径的影响

对图7分析发现，试验频率范围内特别是20～240 Ηz，MRE动刚度随着粒径的增加而增加。在测试频率范围内，不同粒径的MRE动刚度具有一定的线性度（即随着频率提高动刚度线性增加），其中20～160 Ηz频段的动刚度线性度优于 160～240 Ηz频段的动刚；从图9分析可知，无论是NR还是EPDM基体，磁性颗粒粒径对MRE的阻尼特性影响较小，没有明显的规律可循。

4.2.3 磁感应强度的影响

对图8分析发现，试验频率范围内特别是20～240 Ηz，通磁后的MRE较不通磁MRE动刚度明显增大，MRE_EPDM动刚度增加更明显。随着磁感应强度的增加，MRE_NR动刚度没有明显的变化规律，而MRE_EPDM动刚度却不断减小。该试验结果仍然与磁偶极子模型预测趋势相反，即磁感应强度对MRE磁致压缩动刚度特性呈现出负相关特性。为便于进一步分析上述现象，将通磁后的MRE_EPDM动刚度试验数据在全频段内选取40 Ηz、100 Ηz、160 Ηz以及 220 Ηz四个典型频点进行变化趋势对比分析，如图11所示，图中曲线上数据表示不同磁感应强度下的动刚度值（N/mm）。从图中可知，磁感应强度从40 mT增加到120 mT，MRE_EPDM上述四个频点对应动刚度分别降低了10.93%（40 Ηz）、3.99%（100 Ηz）、4.64%（160 Ηz）以及12.18%（220 Ηz），进一步说明磁感应强度对 MRE磁致压缩动刚度特性在宽频范围内呈现出负相关的特性。对于一种减隔振控制系统而言，一旦MRE选定，其基体材料（相对磁导率）以及磁性颗粒（粒径）则相对固定，对MRE性能调控主要通过改变控制电流（MRE所受的磁感应强度）来实现，MRE_EPDM在宽频范围内受磁感应强度影响呈现的规律性对于MRE的控制至关重要。

图11 MRE_EPDM动刚度负相关特性

4.3 MRE动态性能试验与理论预测差异性的原因剖析

从4.2节中发现了基体相对磁导率以及磁感应强度对MRE磁致压缩动态性能在宽频范围内呈现出负相关特性，这与磁偶极子模型预测结果相反。究其原因，可从以下三方面进行剖析：

1）磁偶极子模型假设磁性颗粒间距无限远的状态计算相邻颗粒间的相互作用可能与实际相差较大。实际中，为提高磁流变效应，往往磁性颗粒含量较大（60%以上），因此，磁流变弹性体中集聚结构中磁性颗粒间距则变得较小[15]，此时磁偶极子模型已不适用；

2）磁偶极子模型假设磁性颗粒在基体中均匀分布可能与实际相差较大。磁偶极子模型认为MRE中的颗粒在外加磁场作用下形成一条条相互平行的链，链中颗粒的间距相等，且在基体中均匀分布。而实际上，MRE中磁性颗粒分布、磁性颗粒的极化方向以及各项性能具有强烈的非线性，而且MRE在压缩变形过程中存在颗粒分布重构现象[16]，与假设存在不可忽略的偏差；

3）磁偶极子模型假设磁性颗粒与基体材料完美结合可能与实际相差较大。磁偶极子模型是从能量角度推导磁性颗粒的相互作用关系[17]，磁性颗粒与基体材料之间无能量损耗（前提是磁性颗粒与基体材料完美结合）。而实际上，磁性颗粒的引入不可避免地在MRE中产生结合缺陷甚至孔洞，这与假设存在明显的不同。

5 结束语

通过设计针对性试验方案，对NR、EPDM、MRE_NR以及MRE_EPDM进行了试验对比研究，就MRE基体、磁性颗粒粒径以及磁感应强度三个因素对MRE磁致压缩性能的影响规律进行了试验数据分析，得到以下结论：

1）MRE试验结果与磁偶极子模型预测静态磁流变效应（静刚度特性）趋势完全一致，但与模型预测的动态磁流变效应（动刚度特性、阻尼特性）则趋势不完全一致，甚至出现相反现象。MRE磁致压缩动态性能试验表明，在20～240 Ηz频率范围内MRE_EPDM动刚度随磁感应强度增加而减小，MRE阻尼系数随基体相对磁导率增加而减小，即MRE磁致压缩动态性能在宽频范围内呈现出负相关特性。

2）通过对MRE磁致动态性能负相关特性原因剖析表明，构建磁偶极子模型三个主要假设（前提）条件：磁性颗粒间距无限远、磁性颗粒在基体中均匀分布以及磁性颗粒与基体材料完美结合是造成其磁致压缩动态性能模型预测结果与试验结果造成偏差（甚至相反）的主要原因。由于MRE动态变形时内部结构变化微观层面的复杂性，还需要进一步构建由超弹性、粘弹性和磁性等元件组成的耦合模型，并通过理论推导和试验验证相结合的方式完善MRE本构关系模型，以期更好地预测MRE磁致压缩动态性能，为工程应用提供理论指导。