可变速发电电动机电压波形的优化

胡金明， 苟智德， 王建刚， 孙玉田， 陶大军， 张春莉， 李桂芬， 胡 刚， 贺儒飞

(1.哈动国家水力发电设备工程技术研究中心有限公司，哈尔滨 150040；2.哈尔滨电机厂有限责任公司，哈尔滨 150040；3.大型电机电气与传热技术国家地方联合工程研究中心 (哈尔滨理工大学)，哈尔滨 150080；4.南方电网调峰调频发电有限公司，广州 510950)

0 前言

随着能源消费结构调整的深入和电气化的推进，未来30年，以风电、光伏发电为首的可再生能源将持续快速发展，成为增速最快的能源。在快速转型情景下，预计到达2050年，可再生能源的占比将增长至45%。但是，受到地理位置、气候条件等环境因素的影响，风电、光伏发电等可再生能源的发电功率具有较强的间歇性与不确定性，导致电能质量降低、调频调峰难度增大等问题，影响电网运行的稳定性[1-2]。为了抑制间歇式电源出力的波动性，保证电网的可靠运行，需要在电力系统中增加储能电源。抽水蓄能电站由于其良好的调节性和运行的灵活性，得以大规模发展，在储能中占据领先地位[3-5]。常规抽水蓄能电站采用同步发电机，转速不可调节，使水泵水轮机无法运行在最佳运行区，严重影响水泵水轮机的运行性能和效率[6-8]。可变速抽水蓄能机组相较于常规抽蓄机组的主要优势在于:首先，具备自动跟踪电网频率变化的能力，在水泵工况下，通过平滑调速实现输入功率连续可调，为系统提供了相应的频率自动控制容量；其次，通过改变交流励磁系统输出电压的频率实现转速和有功功率调节，使机组在水轮机工况也能工作在最佳运行区域，提高了运行效率和有功功率调节性能；另外，可变速抽水蓄能机组适应水头和输出功率的变化范围更广、稳定运行区域更宽，并且通过定子绕组短路利用交流励磁装置即可实现零速自起动。因此，发展可变速抽水蓄能机组，对于提高电网安全稳定运行水平以及提升新能源资源利用率等，具有重要意义[9-11]。

可变速发电电动机转子绕组与变流器连接，定子侧与电网连接。变流器利用直流母线电压通过逆变产生三相交流方波电压通入电机转子绕组[12-13]。变流器常用的调制方法有正弦脉宽调制技术、带三次谐波注入的正弦脉宽调制技术、空间矢量调制技术，其中空间矢量调制技术由于其具有数字化程度高、母线电压利用率高的特点备受青睐[14-15]。

电机在正常运行中，定子绕组感应电动势中的谐波会产生谐波电流，进而在电机绕组中产生谐波电动势，引起电势波形的畸变，导致电机本身附加损耗成倍增加，电机绕组温度升高，且会导致电机振动噪声，效率下降，寿命降低，故空载电压波形畸变率可作为考察发电机性能的重要特性[16-19]。本文通过分析其谐波产生的原因提出改进措施，采用斜槽和开辅助槽等方法可以很好的削弱谐波影响，以降低波形畸变，提高电压波形质量，起到降低损耗和温升，提升电机效率的目的[20-24]。

1 空载性能分析

1.1 有限元建模

由于样机定子绕组每极每相槽数为整数，其主要参数见表1，为了便于分析，取一个磁极区域(一半单元电机)作为有限元求解模型。模型的定子外圆gh和转子内圆ab为一类齐次边界条件，ac和bd、eg和fh为半周期边界条件，如图1所示。其瞬态磁场采用矢量磁位描述，假设位移电流及定子铁芯中的涡流忽略不计，定、转子绕组端部漏抗通过电路方程和电磁场方程耦合计入，则电机内二维瞬态电磁场方程的边值形式可由式(1)表示。

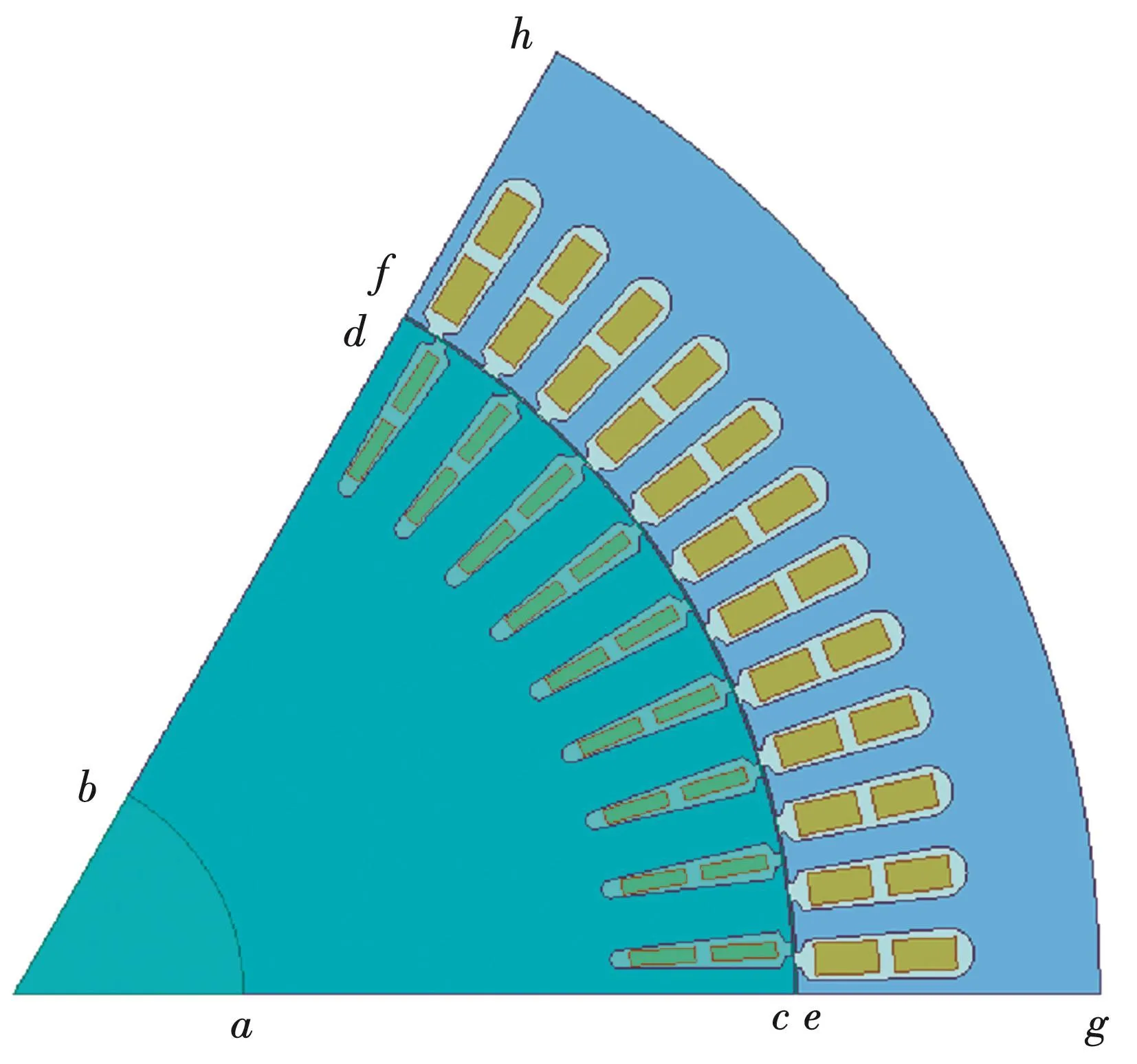
图1 求解场域

表1 样机主要参数

1.2 空载工况有限元仿真

依据90kW样机的结构特点采用瞬态磁场有限元法对其空载磁场进行了分析，为准确获得有限元计算结果，需适当加密网格剖分，如图2所示。转子绕组通入三相正弦交流励磁电流，瞬态场求解后其磁场分布如图3所示，磁密分布如图4所示，三相线电压波形如图5所示。

图2 有限元网格剖分

图3 空载磁场分布

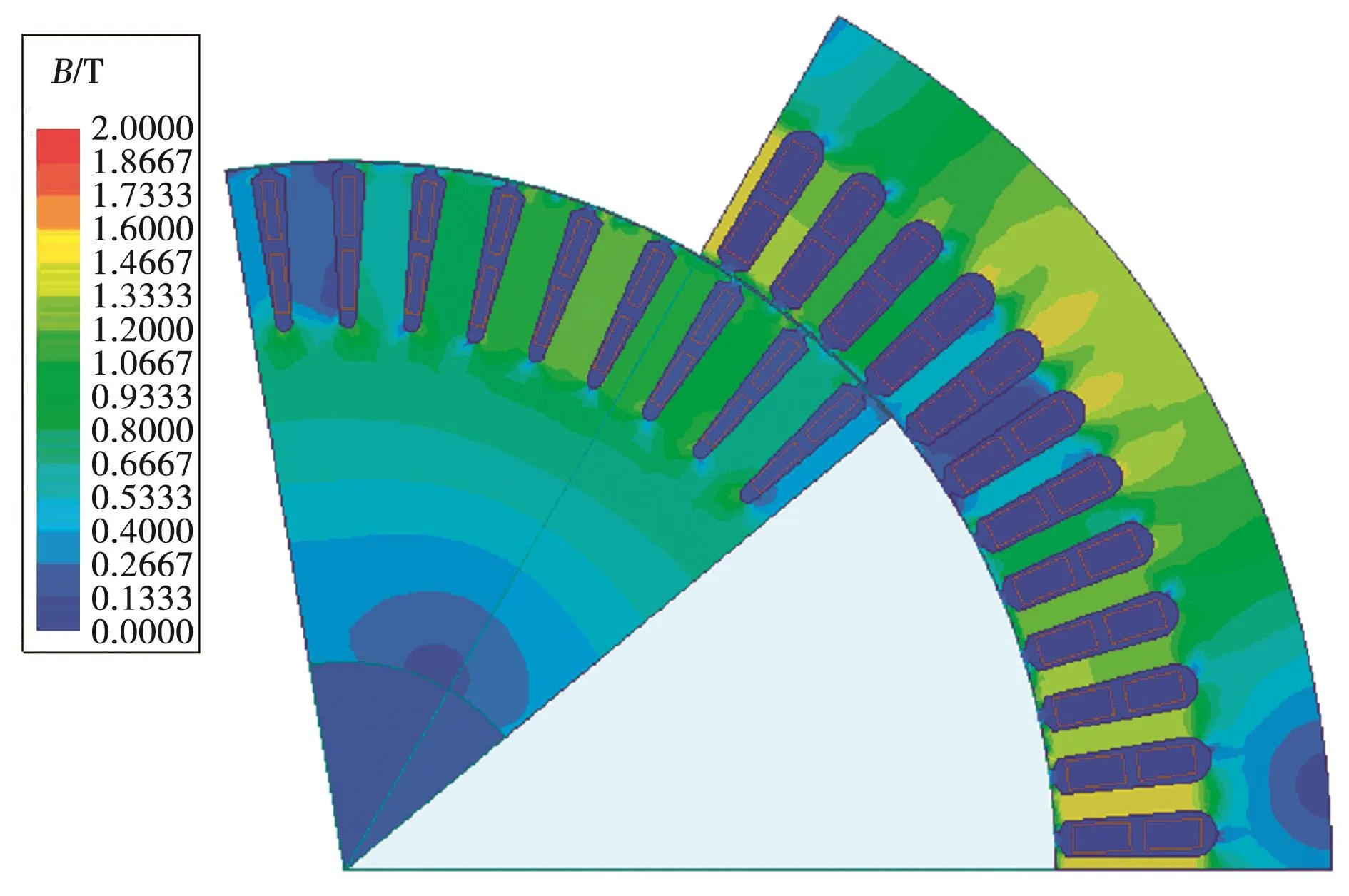
图4 空载磁密分布

由图5可见，本台样机的电压波形质量较差，波形畸变严重，取空载电压一个周期波形，对其进行傅里叶分解，谐波分布如图6所示(为分析谐波情况，图中未绘制基波)。根据文献[14]计算得到空载线电压波形畸变率为7.58%，超出国家标准 《旋转发电机定额和性能》(GB 755)规定。

图5 三相线电压波形

图6 谐波分布

2 谐波来源分析

2.1 变流器谐波对电压波形的影响

可变速发电电动机转子绕组连接变流器，变流器输出电压为由常用的空间矢量调制方法(SVM)调制得到的方波电压，含有多频次谐波。本文提取转子电压中的谐波，将其作为有限元分析的边界条件，对比分析转子谐波下定子侧波形畸变。

当可变速发电电动机并网空载运行时，定子绕组电流为0，其状态方程:输入向量为u＝[udruqr]T，状态向量为 x＝[idriqr]T，输出向量为 y＝[udsuqs]T，方程如式(2)所示，使用此状态方程可搭建空载电机模型。

此时电磁转矩为0。

利用SVM调制技术建立如图7所示的开环控制下空载工况仿真模型。

图7 基于SVM的可变速电机空载仿真模型

仿真得到SVM调制的转子电压如图8所示，定子电压如图9所示，对转子电压进行傅里叶分解得到谐波分布如图10所示，包含多频次谐波。

图8 SVM调制的转子电压

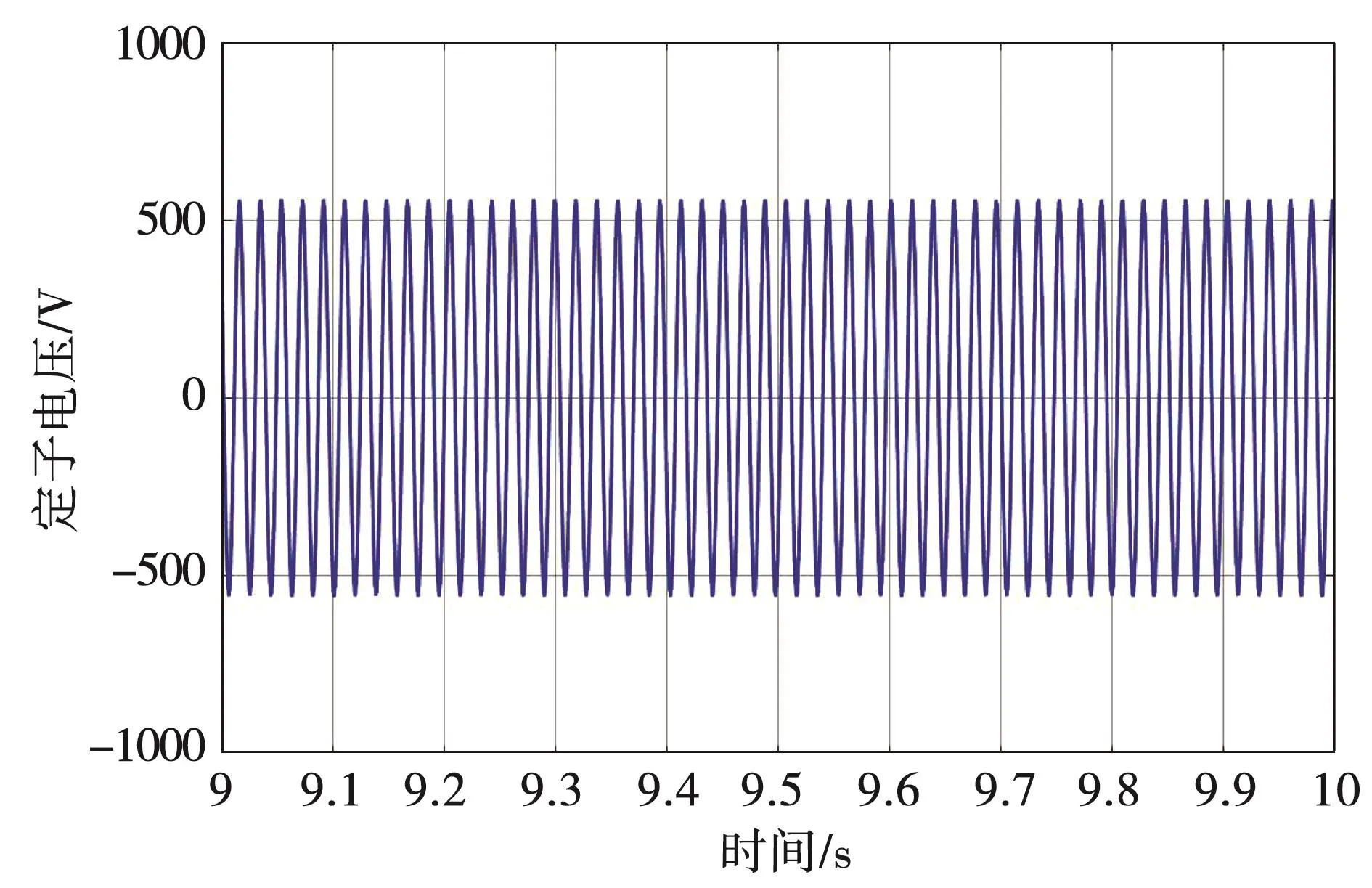
图9 定子电压

图10 转子电压谐波分布

提取变流器的谐波分布作为有限元仿真的励磁电流边界，如下式:

式中，Iar、Ibr、Icr分别为转子三相励磁电流；IF为基波励磁电流幅值；IFv为v次谐波励磁电流幅值。

仿真得到考虑变流器谐波和不考虑变流器谐波情况下定子电压的对比如图11所示，观察图11可以看出，考虑变流器谐波后，定子电压的波形变化不大。对考虑变流器谐波的定子电压波形进行傅里叶分解后谐波分布如图12所示，波形畸变率为7.94%，相比不考虑变流器谐波时有所增大，故变流器谐波对电压波形有些影响，需要在电机设计时予以考虑。

图11 定子电压对比

图12 谐波分布

2.2 电机本体齿谐波对电压波形的影响

由于电机铁芯齿槽部分的磁导率不同，气隙磁通密度的分布波形会受到影响，齿下气隙较小磁导大，反之槽口气隙大磁导小，影响绕组里的感应电动势波形，造成波形中出现较强的高次谐波，即齿谐波。

仔细观察图6和图12谐波分布图可以发现，在次同步速900r/min时高次谐波中64次和66次谐波幅值较大，即为此电机的齿谐波。为找出其齿谐波的分布规律，本文仿真不同转差率下定子电压齿谐波的分布情况，见表2。

表2 齿谐波频次

通过表2可以得出可变速发电电动机的齿谐波满足如下公式，为可变速发电电动机的特有齿谐波性质。

式中，λ为齿谐波次数；s为转差率；k为常数1、2、3…；q1、q2分别为定、转子每极每相槽数。

3 样机试验与优化

3.1 样机试验

样机试验平台由拖动机、可变速发电电动机样机、变流器组成，实物如图13所示。

图13 样机试验平台

对可变速发电电动机进行了空载特性试验，试验过程为:保持在额定转速下，调节励磁电流从1A增加至21A，记录定子线电压有效值。试验值与有限元仿真值对比结果见表3，绘制曲线如图14所示。

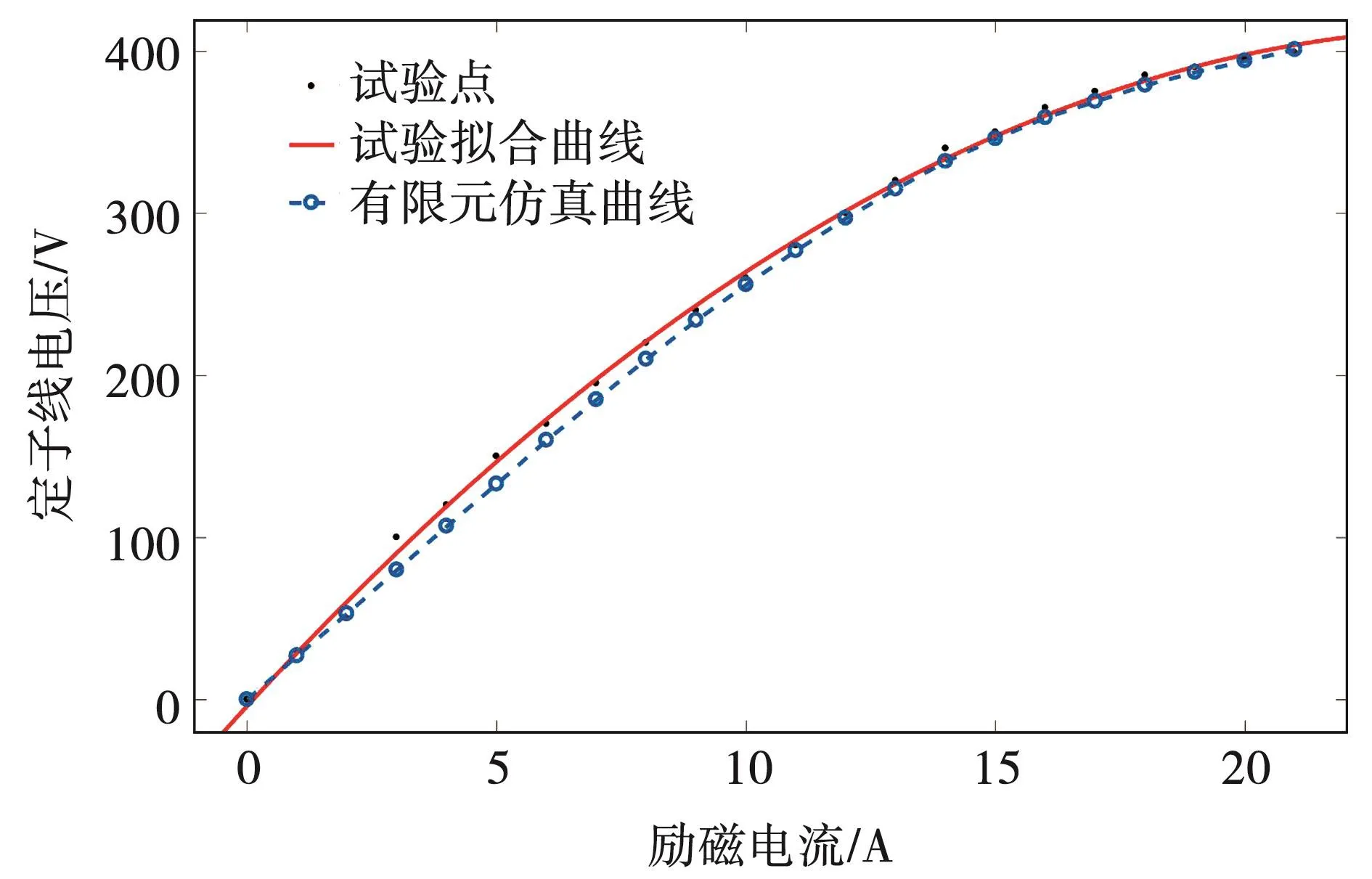
图14 空载特性曲线对比

表3 空载特性对比值

对比空载特性曲线的仿真值和试验值可以看出，其结果差异很小，可以证明有限元仿真结果的正确性。试验并网前后定子绕组的开路电压如图15所示。由图可知，并网前定子线电压波形畸变率较高。

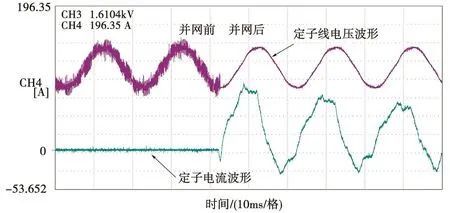
图15 并网瞬间定子电压、电流波形

3.2 电压波形质量的优化

齿谐波不能通过采用分布式绕组或绕组短节距的方法加以消除或者削弱。齿谐波是由于齿槽部分的磁导不同造成的，如果采用半闭口槽、磁性槽楔、或者无铁芯结构，则可以削弱甚至不会产生齿谐波，另外通过增加每极每相槽数、斜槽、分数槽等均可以大幅度削弱电势齿谐波。本文综合考虑后，决定采用斜槽和在定子齿上开辅助槽 (辅助槽局部放大如图16所示)的方法来削弱齿谐波的影响。

图16 辅助槽局部放大

分别仿真分析定子斜槽 (1°～8°)，定子开半圆型辅助槽 (半径1～2mm)、转子开半圆型辅助槽(半径1～2mm)。波形畸变率对比见表4。

表4 波形畸变率对比

电机的气隙比磁导为:

式中，μ0为真空磁导率；δ为气隙。

由上式可知，在定子上开辅助槽相当于降低电枢表面平均比磁导，虽然会少量增加励磁磁势，但可有效改善电枢磁势波形，进而降低电压波形畸变率。此方法可适用于不同齿宽，建议辅助槽直径在0.5～0.8倍的定子槽宽范围内选择，本文所用样机的定子槽宽为4mm。

由表4可知，在定子斜槽5°(一个齿距)和定子开半径为1.2mm辅助槽 (辅助槽直径为0.6倍槽宽)时波形畸变率最小，谐波得到有效削弱，说明这两种方法对削弱齿谐波是有效的。

最后，将这两种优化方法结合，重新进行有限元分析，得到空载电压波形如图17所示，谐波分布如图18所示，此时波形畸变率为1.17%，此台样机得到了很好的优化。

图18 优化后电压波形谐波分布

4 结论

本文对一台90kW可变速发电电动机样机进行研究，利用有限元法分析其空载谐波特性，仿真表明，样机的电压波形畸变较大，超过标准要求的限值。分别考虑变流器谐波和电机本体齿谐波对空载电压波形的影响。变流器谐波会导致电压波形质量下降，通过对本台电机齿谐波的研究，发现其齿谐波与转差率和定、转子的每极每相槽数相关。试验对比有限元仿真的空载特性曲线和试验的空载特性曲线基本一致，证明了有限元仿真的正确性。为改善电压质量，本文采用定子斜槽、定子和转子开辅助槽的方法大幅度降低了定子电压的波形畸变率，优化结果表明，在考虑变流器谐波的影响下，谐波畸变率仍满足标准要求。