基于有效摩擦因数的顶管隧道摩阻力计算方法研究
邹洋,彭立敏,雷明锋,叶艺超,施成华
(1.中南大学 土木工程学院,湖南 长沙 410075;2.垒知控股集团有限公司,福建 厦门 361004)
随着我国经济的高速发展和地下空间的大规模开发利用,顶管法以其安全性高、环境影响小等特点,在城市交通等地下基础设施建设中得到了广泛应用[1]。在顶管工程中,顶进力是管节结构设计、顶推设备选型以及工作井结构设计的重要依据,直接关系到建设过程中的结构安全及工程造价[2]。顶管顶进力由刀盘迎面阻力和管壁摩阻力两部分组成,而随着顶管顶进长度的增加,管壁摩阻力逐渐增大,在顶推力中起到控制作用[3−4]。尽管国内外学者对顶管顶推力的预测进行了大量研究,但在实际应用中仍存在一定的问题,其技术难点主要体现在顶管隧道的摩阻力难以准确预估。此外,顶管顶进过程中大多采用在管节与土层间注入泥浆的施工措施,以降低顶管摩阻力,而对注入泥浆减阻效果的分析及相关理论研究尚有不足。目前,泥浆顶管摩阻力的主要计算方法有以下3类:1) 仅考虑管−土摩阻力,忽略泥浆的减阻效果。O’REILLY等[5]基于开挖面稳定、管−土全接触假设,采用管土“固—固”接触方式推导得到了顶管摩擦力。MILLIGAN等[6]认为在管壁稳定条件下,通过计算管−土摩阻因数与其自重的乘积来计算顶管隧道的摩阻力。HASLEM[7]则进一步提出考虑管−土部分接触模型,并基于Hezrt接触模型,推导得到管−土摩阻力与管−土黏着力和接触宽度之乘积有关。该类方法在工程中的应用简便,有一定适用性,但忽略了泥浆的减阻效果,计算结果偏大。2) 只考虑管−泥浆摩阻力,不考虑管-土摩擦力,即假定管节处于理想悬浮状态,不与孔壁接触。王双等[8]考虑减阻泥浆的作用,利用流体力学理论探讨了注浆压力对泥浆套厚度的影响,并针对3种泥浆套形态分别提出了摩阻力的计算方法。叶艺超等[2]基于半无限空间柱形圆孔扩张理论和平板模型,也提出了考虑减阻泥浆影响的顶推力计算方法,并通过实例进行了可靠性验证。喻军等[9]通过室内模型试验研究了注入泥浆对顶管顶推力的影响,指出泥浆条件下顶管摩阻力可降低72%。NAMLI等[10]通过试验指出,即使在连续注入泥浆压力非常低的条件下,管−土之间的泥膜界面仍可形成且能够减少砂—混凝土管节大约90%的摩擦力,但在不连续注浆的情况下,减阻效果有限。总之,该类方法忽略了管−土摩擦效应,与实际的顶管状态存在一定差异。3) 同时考虑管−土摩擦力和注浆泥浆的影响。SHIMADA等[11]基于1/3管−土接触面和2/3管−浆接触面的假设,以管径0.8m的混凝土顶管为例计算了总摩阻力,并与工程实际数据做了对比。这种假设带有明显的人为性,且管−土接触宽度是与地层参数有关的量,有待进一步分析。SHOU等[12]在SHIMA‐DA基础上,通过Hezrt接触模型计算管−土的接触角与接触宽度,得到了同时考虑2种界面摩擦特性的顶管摩阻力计算方法。MILLIGAN等[6,13]通过管−土全接触模型、管−土部分接触理论计算值与顶管摩擦力实测值的对比,得到了管−土全接触理论的摩擦力计算值比实测值大,而管−土部分接触模型的摩擦力计算值比实测值略小的结论。CHAP‐MAN等[14]通过分析不同地质条件下的顶管工程案例数据,得到了不同地质条件下的顶进力预测经验公式。张鹏等[4,15]在同时考虑管−土接触与管−浆接触,并在假定管节弹模与岩土近似一致的情况下,利用Persson接触模型分析管−土接触力学特性,同时考虑管−泥浆摩阻力,推导出顶管顶进力计算公式。SHOU等[16]采用不同的润滑材料,通过室内直剪试验研究了混凝土块与土体界面的摩擦力特性,并在室内试验基础上采用经验公式预测了顶管顶进力。总之,该类方法虽然同时考虑了管−土接触与泥浆减阻效果,但对于管−土接触及管−泥浆接触宽度的考虑大多是基于经验或者实验,相应的理论分析较少。综上分析可见,目前对于顶管摩阻力的计算,大多基于经验估计、完全理想假定的条件或者针对特定的工况条件进行,且各种方法中摩阻力值的大小存在较大的偏差,同时对其影响因素的分析不够全面。实际上,影响顶管摩阻力的因素是非常复杂的,CHAPMAN等[14]统计了47个工程实例,发现摩阻力与管节直径呈正相关关系。另外,PELLET等[17]分析了6个工程实例,发现摩阻力还与施工间隙、停机时间以及土层颗粒大小(或空隙的大小)是有关的。因此,也极有必要进一步分析这些因素对摩阻力大小的影响。
为此,本文运用摩擦学的基本原理,考虑既有的土压力计算模型与Persson接触模型,基于管−土、管−泥浆不同的接触比例,结合相应的管−土摩擦因数、管−泥浆摩擦因数,提出一种适用于考虑泥浆减阻效应的顶管摩阻力计算方法,并就其影响因素开展参数分析。
1 顶管土压力计算模型
1.1 管节正压力计算
假定顶管各点受土压力作用的径向应力为σn,结合对称性原理,管周的径向荷载可统一表示为:

式中:Dp为管节外直径;θ定义为管节各点处半径线与水平线的夹角,逆时针方向为正,顺时针方向为负,如图1。

图1 顶管结构受力示意图Fig.1 Earth pressure and normal stress acting on the pipe
顶管土压力可以简单地分解成垂直土压力和侧向土压力(图1),故径向应力为:

式中:σh为管节外周各点的竖向应力;σh为管节外周各点的水平应力,σh=Kσv,K为侧压力系数。
将式(2)代入式(1),得到:

1.2 3种垂直土压力计算方法
由式(4)可知,管节正压力N取决于垂直土压力σv。而目前,关于垂向土压力的计算方法有太沙基理论、英国“UK PJA”法和德国“ATVA 161”法。
1) 太沙基方法
太沙基法[13]是应用最为广泛的土压力计算方法。假定土体为具有一定黏聚力的散体,认为孔洞开挖时,上覆地层沿着如图2(左)所示的平面产生松动滑移,则竖向土压力为:

图2 土压力计算示意图Fig.2 Boundary planes of soil model

式中:h为隧道覆土高度;γ为土体重度;c为土体黏聚力;φ为土体内摩擦角;δ为管−土摩擦角;b为土层松动的影响宽度。
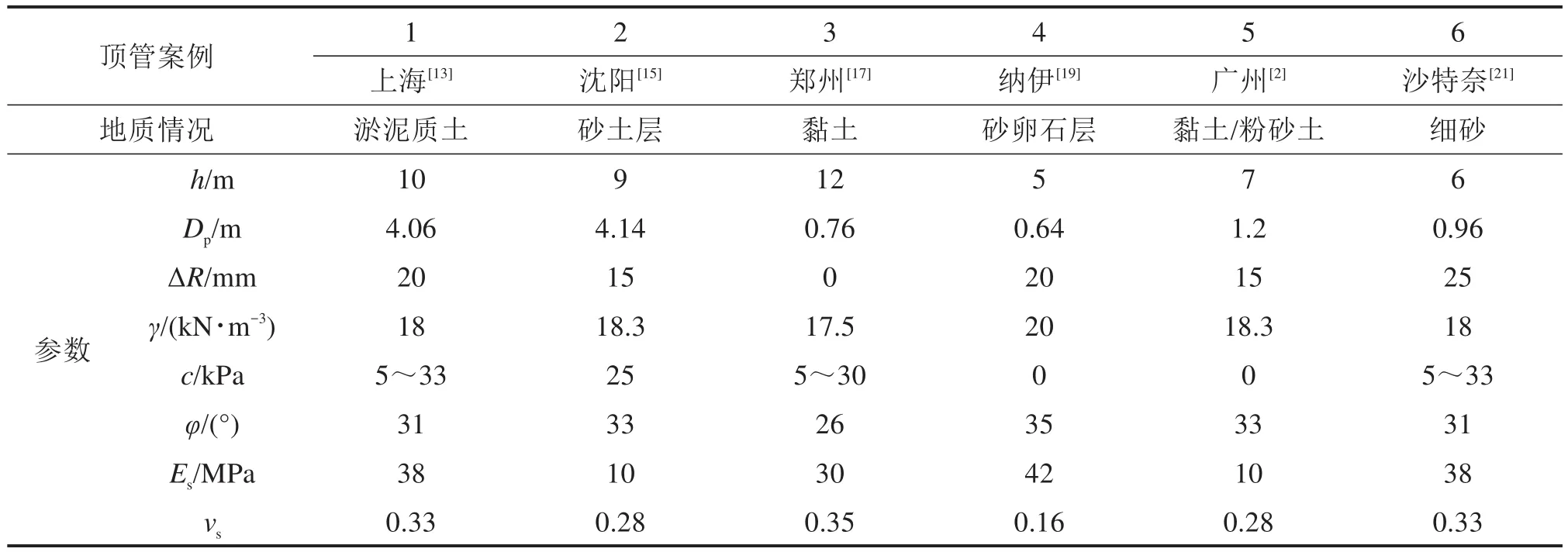
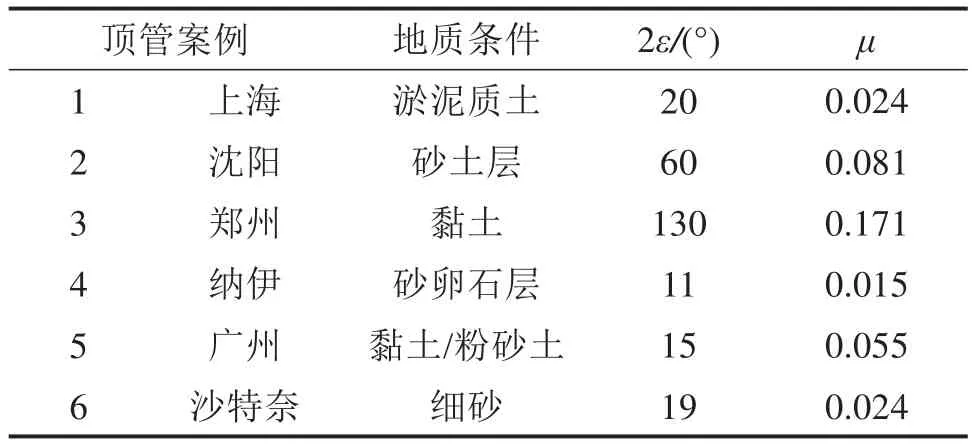
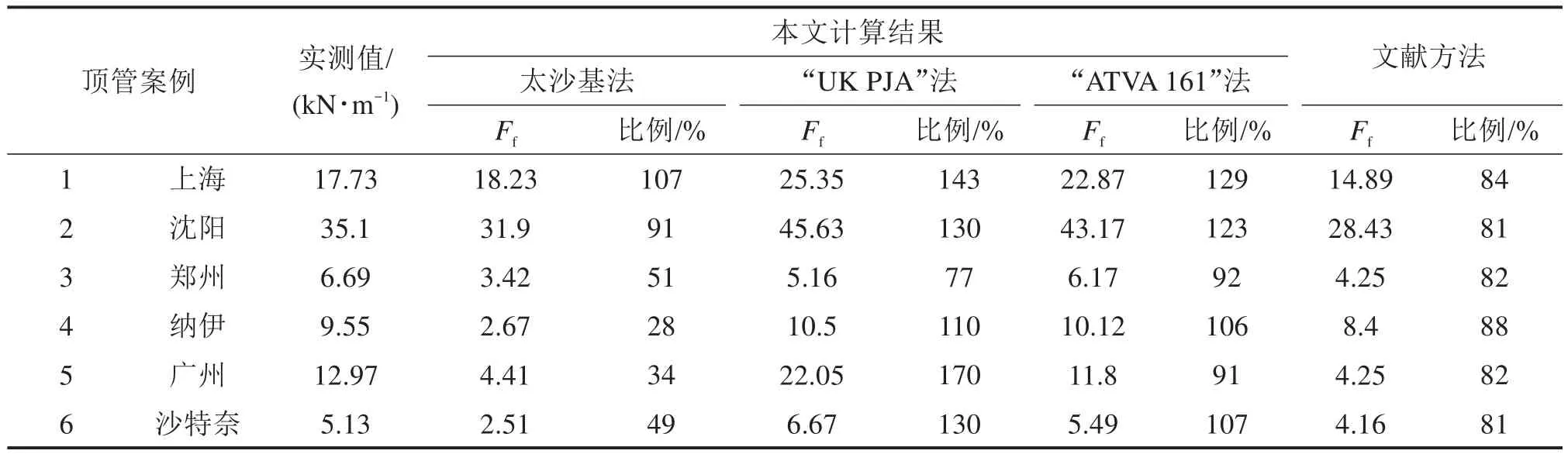
值得注意的是,当隧道的埋深较浅时(h 式中:k为折减系数,k越大,土层的“拱效应”越显著,反之亦然;b=Dp(1+2tan(π/4-φ/2));δ=φ;K=1。 2) 英国“UK PJA”法 尽管目前各国相关研究人员普遍接受了太沙基土压力理论,但是在模型计算参数(b,δ和K)的确定方面,却产生了分歧。最具有代表性是UK PJA针对滑移面提出的改进模型,如图2(右),相应参数取值满足:b=Dptan(3π/8-φ/4),δ=φ,K=(1-sinφ)(1+sinφ)。 3) 德国“ATVA 161”法 ATVA 161[13]也在太沙基模型上做出了一定改进,如图2(右),不过将内摩擦角统一取为常数30°。不难发现,本模型具有更小的影响宽度b,这就增大了系数k,即增强了土层的“拱效应”,故其计算的土压力显然要比初始的太沙基模型要更大,其参数取值为b=Dp,δ=φ/2,K=0.5。 PELLET等[17]对上述3种土压力计算方法进行了对比分析,发现按照“ATVA 161”法计算的松动土压力结果最大,而按照太沙基初始模型的计算结果最小,“UK PJA”法界于两者之间。尽管如此,但PELLET未对这3种方法的适用性进行研究。 顶管施工过程中泥浆的使用改变了管−土接触特性。理想状态下,注入的泥浆体完全填充施工间隙,与接触部位土体不发生互相渗透,或者短时间后,渗透行为停止,并使泥浆与土体交界区形成一层致密的泥膜,既避免管节与土体直接接触,同时保证泥浆具有一定的压力以维持孔洞稳定[18]。此时,管节顶进时的摩擦阻力仅取决于“管节−泥浆”的物理特性。 但更为一般的情况是,由于注浆量的设计与控制、孔洞周围土体的不规则变形、顶进线路的偏移、泥浆与土体之间的互相渗透及管节内外力的综合作用,管节通常一部分与土体发生接触,接触行为也由单一的“管节−泥浆”接触模式转变为更复杂的“管节−泥浆−土体”混合接触模式,如图3。即,在实际工程中,可认为整个顶管与周边的接触宽度可分为管节−土体的接触宽度Bs,与管节−泥浆的接触宽度Bm两部分之和。 图3 管−泥浆−土接触模型Fig.3 Contact model and symbols used 在这种情况下,计算摩阻力时需要考虑管−土接触的位置、角度(或宽度)大小及接触力,才能计算出准确的结果。为此,考虑顶管工程实际条件,对顶管施工过程做出如下假设: 1) 管−土接触位置在顶管横向各个位置出现的概率是相同的,考虑重力的影响,认为管−土接触通常位于底部。 2) 不同接触方式对接触土压力大小没有影响。 3) 不考虑泥浆对土体的渗透过程,注浆不影响土体性质。 经典的摩擦力学认为摩擦力可以统一表述为摩擦因数与作用于物体表面的总径向荷载的乘积: 式中:Ff为顶管总摩擦力;μ为泥浆、土层与管节之间的有效摩擦因数。 在平面应变的假设下,N为作用于单位长度管节上的总径向荷载,单位kN/m。然而,对于泥浆顶管工程,如何准确的计算N和μ却并不容易。特别是μ的确定,迄今仍未见适用于泥浆顶管的计算方法。目前的研究中,摩擦因数一般认为是一个常数,仅依赖于土层特性,即: 当单纯地考虑管节与土体的相互作用时,人们普遍将管体与土体之间的摩擦角δ取为土层内摩擦角φ,滑动摩擦力取为φ/2[17]。而对于泥浆顶管,不同学者有不同的看法,δ可能取为土层内摩擦角φ/2~φ或φ/3~φ/2。正如前文所述,这样的取值方法过于宽泛且没有考虑泥浆的润滑作用。 泥浆顶管的摩擦力Ff可以分成管节−土体摩擦力Fs和管节−泥浆摩擦力Fm之和,即: 根据假设(1)与假设(2),泥浆顶管的有效摩擦因数与接触压力大小及接触位置无关,这就使得该问题大大的简化,于是可得: 式中:C表示管节的外周长;Bs,Bm分别表示一个环向周长中管节和土层、泥浆的接触宽度。 将式(9)、式(10)代入式(8)中,有 式中:λs表示管节−土体的接触比例;λm表示管节−泥浆的接触比例;2ε为与接触宽度Bs对应的接触角(如图3);μs表示管节与土层动摩擦因数;μm表示管节与泥浆的摩擦因数。 由式(12)~式(14)可知,计算有效摩擦因数的关键在于计算管节与土层的接触宽度Bs(或接触角度2ε)。根据顶管施工的技术特点,多数顶管工程穿越的是黏土或砂土地层[19]。接触角度值在一个范围内变化(存在接触角较大的情况),应采用应用较广泛的Persson接触模型[20]进行计算,即: 式中:ΔR为顶管隧道施工间隙(计算中视为泥浆套厚度);νp和νs分别为管道和土体泊松比;Ep和Es分别为管节和土体弹性模量;P为作用于管节中心的外荷载,当孔洞稳定,管节在重力作用下底部与土层接触,此时,P等于单位长度管节的重力,其他参数的意义如下: 式(16)是一个复杂的非线性方程,需进行简化处理以便于应用。针对顶管隧道[4],认为在硬地层条件下管节的弹模Ep与土体的弹模Es的大小相差不大,则可求得接触角度2ε的显示表达式。但对于多数顶管工程穿越地层为土层的情况,管节弹模Ep与土体弹模Es的大小存在显著差距,Es一般为10 MPa量级,而混凝土材料管节弹模Ep则为104MPa量级,即Es远小于Ep。因此,文献中认为管节弹模与岩体弹模大小相差不大的情况并不适用于常见顶管穿越土层的工程案例。对此,本文针对工程实际情况,做出以下改进。 根据式(16)有: 当Es< 对于式(12)左边有: 而对于式(15)右边,当η≥103时,代入式(16)有: 综上,式(12)可以简化为: 联立式(16)和式(23)即可确定唯一的管土接触角度 2ε(或接触宽度)。 综上分析,有效摩擦因数μ可由管土摩擦因数μs,管-泥浆摩擦因数μm,管-土接触的分形系数λs确定;而管节正压力N与隧道覆土高度h,土体重度γ,土体黏聚力为c,土体内摩擦角为φ,管-土摩擦角为δ有关的变量,μ和N的表达式可写为: 管节与土层动摩擦因数μs,可在实验室测取或在相关地质资料查得,本文参考文献[17]取μs=tan(φ2)。在实际顶管施工过程中,泥浆可以大大降低顶管−土层之间的摩阻力,因此可以认为管−泥浆的摩擦因数是小于管−土摩擦因数的,即μm与μs存在一个差值Δμ(通常为一个正值),根据相关研究表明[9−10],Δμ的取值一般在80%~90%之间,具体取值依据实际工程案例决定。式中其他参数γ,φ,c,h,Es,ΔR,P,νs均可以通过相应现在数据取得。于是,将式(22)~式(26)代入式(6),即可求得顶管摩阻力Ff,计算流程如图4所示。显然,摩擦因数μ不再仅仅依赖于地层特性参数(Es,vs及P),还考虑了设计参数(h,Dp和ΔR)的影响。也就是说,对于某个具体的泥浆顶管工程,复杂的地质条件决定了有效摩擦因数μ可能不是一个常数,而是在某个范围内变化。 图4 顶管摩阻力计算流程图Fig.4 Flow chart of friction resistance calculation 从既有文献中收集了6个钢筋混凝土顶管工程的基本参数及对应实测数据,如表1,表中地层参数原则上按照工程实例中给出的参数进行计算,少数缺失的参数按照《工程地质手册》[22]进行选取。 表1 不同地质条件的顶管案例参数Table 1 Parameters which are needed to calculate the prediction equations in each case 表2给出了表1所述案例中管土接触角度及相应有效摩擦因数的计算结果。从中分析可见,泥浆顶管的有效摩擦因数一般在0.015~0.171范围之间。案例3的径向间隙为0,使得计算的接触角高达130°,间接导致了一个很大的摩擦因数0.17。若排除案例3,当顶管直径在0.6~4.0 m范围,有效摩擦因数在0.015~0.081之间,而管土接触角的值在11°~60°之间。由此可见,管土接触的比例与文献[11]提到的1/3管土接触面和2/3管浆接触面的情况存在较大的差异。 表2 顶管案例有效摩擦因数计算结果Table 2 Calculated value of effective friction coefficient of pipe jacking case 表3给出相应案例摩阻力的计算结果及其对比情况。从中分析可知: 表3 不同土压力条件下顶管案例的摩阻力计算结果Table 3 Comparison of the friction resistances calculated by the new approach and the measured data 1) 非越江隧道工程(案例3~6)中,基于太沙基法的摩阻力计算结果普遍偏小,这是因为其垂直土压力的计算结果较小,导致了管−土接触角度偏小。 2) 基于“ATVA 161”法和“UK PJA”法推荐的修正模型计算的摩擦阻力均与实测结果相吻合,说明这2种方法计算顶管摩阻力的结果都较为准确。 3) 对于越江顶管工程(案例1~2),太沙基计算方法则表现出了比“ATVA 161”法和“UK PJA”法更好的结果,这可能是由于富水环境下开挖隧道,其地层影响宽度b更大,该模型假设的滑动面更接近实际情况。因此认为越江泥浆顶管隧道中宜采用太沙基方法计算土压力,而对于非越江隧道,则德国方法推荐的模型更为合理。 进一步取土体重度为20 kN/m3,黏聚力为15 kPa,摩擦角为25°,土体弹模为25 MPa,土体泊松比为0.25,管−泥浆摩擦因数为0.01时的参数,对不同埋深h,不同管径DP和不同施工间隙ΔR3个典型因素对管土接触角、有效摩擦因数和顶管摩阻力的影响规律进行分析。 取顶管直径为2 m,施工间隙为20 mm,当埋深h分别从5 m增加到30 m时,得到接触角度、摩擦因数及摩阻力随埋深的变化关系如图5。分析可见三者与埋深h的关系基本呈平缓的线性增长关系,埋深在30 m以下时,接触角度2ε大小不超过35°。埋深的增大对摩擦阻力的增大具有双重作用:首先,其值的增大增加了管道与土壤的接触角2ε大小,从而增加了界面有效摩擦因数μ;其次,埋深的增加增加了竖向土应力,但总来说附加摩擦力受埋深的影响不大。当埋深大于20 m时,接触角度2ε,摩擦因数μ,摩阻力f的大小基本变化不大。 图5 埋深h对计算结果的影响分析Fig.5 Influence of h on calculations 同理,取顶管直径为2 m,施工间隙为20 mm,当管径从1 m增加到4 m时,得到相应的计算结果如图6。 图6 管径DP对计算结果的影响分析Fig.6 Influence of DP on calculations 分析可见,接触角度2ε,摩擦因数μ随管径的增大,基本呈线性增长;而顶管摩阻力随管径的增大呈抛物线增长。管径的增加,不仅增加了管土接触的角度2ε与有效摩擦因数,更增加了作用在管道上的总径向力N。当管径从1 m增大到4.0 m时,摩擦阻力从0.34 kN/m显著增加到48.16 kN/m。因此,顶管摩擦力受管径的影响较大。 取顶管直径为2 m,埋深为10 m,当施工间隙从0~50 mm时,得到相应的计算结果如图7。分析可知,接触角度2ε,摩擦因数μ,摩阻力f与施工间隙ΔR基本呈反比例关系。当ΔR从0 mm增大到50 mm时,管土接触角度显著减少,管土接触角度的减少,即反映着顶管泥浆减阻效果的提升,因此图7中的有效摩擦因数μ和摩阻力f均呈现出下降趋势。尤其当ΔR小于20 mm时,管土接触角度、有效摩擦因数和顶管摩阻力的值都较大,因此在保证顶管施工孔洞稳定性的基础上,适当增大施工间隙可有效减少摩阻力Ff,建议顶管施工时的施工间隙不应小于20 mm,以保证较好的泥浆减阻效果。 图7 施工间隙ΔR对计算结果的影响分析Fig.7 Influence of ΔR on calculations 1) 顶管的有效摩擦因数取决于管−土摩擦因数、管−浆摩擦因数及交界面接触状态,当注浆效果良好时,有效摩擦因数在0.01~0.1之间变化; 2) 顶管管−土接触角,不仅受到地质参数的影响,与埋深、管径及施工间隙等设计参数也息息相关。具体为,与埋深和管径呈正相关关系,与施工间隙呈负相关有关系;混凝土顶管直径在0.6~4 m范围,接触角度普遍在10°~60°之间; 3) 顶管施工时应保持20 mm以上的施工间隙,以保证较好的泥浆减阻效果; 4) 对于富水条件下的钢筋混凝土顶管隧道摩阻力计算,宜采用太沙基计算土压力,而对于非富水情况,则ATVA 161推荐的修正模型更为合适。
2 摩阻力计算方法
2.1 计算模型

2.2 有效摩擦因数




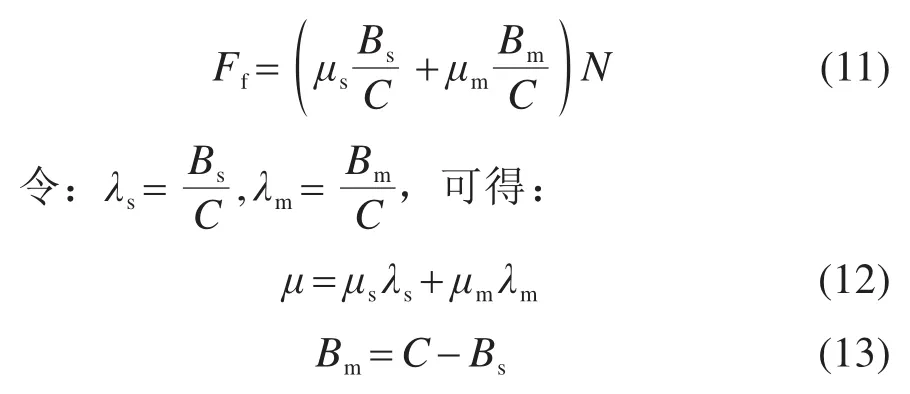

2.3 管−土接触角
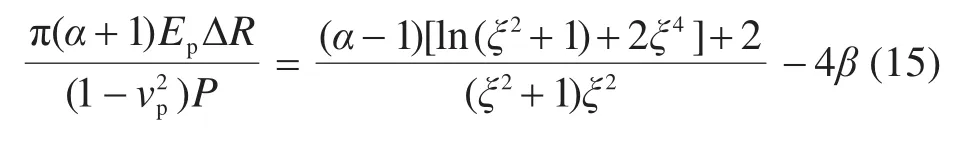
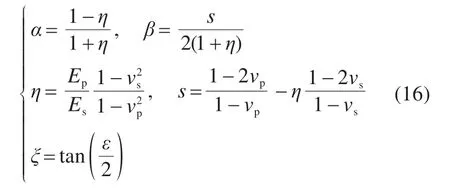
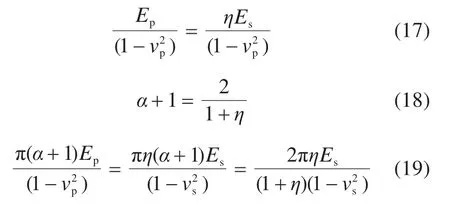



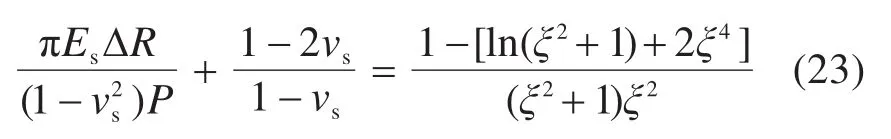
2.4 顶管摩阻力计算
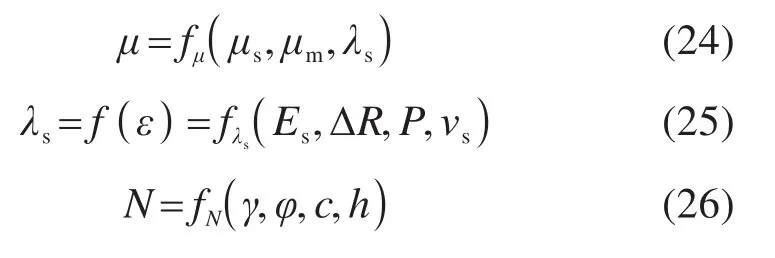

3 工程实例验证
3.1 计算参数
3.2 有效摩擦因数计算结果
3.3 顶管摩阻力计算结果
4 参数影响分析
4.1 埋深h的影响

4.2 管径Dp的影响
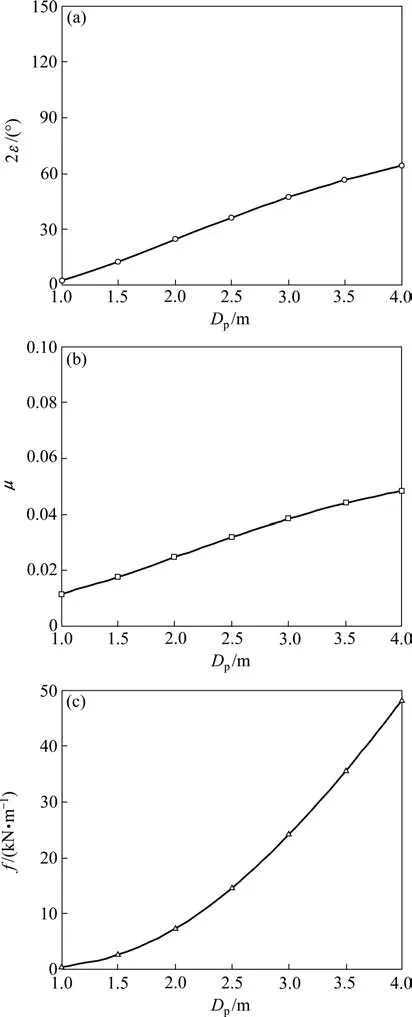
4.3 施工间隙ΔR的影响

5 结论

