具有Robin边界的坏死核非线性肿瘤生长模型整体解的存在性*

吴 攸

（广东工业大学数学与统计学院，广东 广州 510520）

0 引 言

肿瘤生长规律的数学研究，很早就引起了人们的重视 .早在 20 世纪 70 年代，Greenspan［1］考虑了肿瘤内营养物质的反应扩散和由此导致的肿瘤细胞的繁衍与死亡，首先用偏微分方程自由边界问题来描述肿瘤的生长.由于肿瘤所占据的空间区域和边界是随时间不断变化并且不是预先给定的，需要与其他未知函数一起确定，所以自20世纪90年代末以来，这一课题引起了以国际著名偏微分方程专家和应用数学家Friedman院士为代表的一批偏微分方程工作者的极大兴趣，其研究在过去20多年中取得了长足的发展，并涌现出了众多出色的研究成果，已成为偏微分方程研究领域的一个新的热点研究课题.

Byrne 和 Chaplain［2］提 出 了 关 于 肿 瘤 生 长 的Byrne-Chaplain模型，该模型的边界条件包括Dirichlet自由边界和Robin自由边界，根据模型中是否包含坏死核，可以将模型进一步细分为有坏死核的肿瘤生长模型和无坏死核的肿瘤生长模型；Fried‐man 和 Reitich［3］研究了 Dirichlet自由边界条件下的无坏死核的肿瘤生长模型，得到了整体解的存在唯一性以及解的渐近性态；Cui和 Friedman［4］研究了Dirichlet自由边界条件下的有坏死核的肿瘤生长模型，得到了解的适定性以及解的渐近性态；Friedman和Lam［5-6］研究了Robin自由边界条件下的无坏死核的肿瘤生长模型，得到了稳态解的存在唯一性，并对解的渐近性态进行了讨论；Shen和Wei［7］研究了Robin自由边界下的无坏死核的肿瘤生长模型，得到了整体解的存在唯一性以及解的渐近性态；沈海双等［8］研究了Robin自由边界条件下的有坏死核的肿瘤生长模型，得到了稳态解的存在唯一性.上述文献所研究的模型中，描述营养物浓度和抑制物浓度的函数均为线性函数.在基于生物学和医学实际的前提下，卫雪梅和崔尚斌［9-10］进行了肿瘤生长模型包含非线性函数的研究，并得到了模型整体解的存 在 唯 一 性 和 渐 近 性 态 ；Cui［11］、Wei［12］、Wu 和Wang［13］、Bueno 等［14］研究了有坏死核的非线性肿瘤生长模型在Dirichlet自由边界条件下解的适定性；Zhuang 和 Cui［15］研究了 Robin 自由边界下无坏死核的非线性肿瘤生长模型，得到整体解的存在唯一性；Zheng 和 Cui［16］研究了 Robin 自由边界下无坏死核的非线性肿瘤生长模型解的渐近性态.

事实上，对于有坏死核的肿瘤生长模型而言，其生长可以分为2个阶段，假设σD为肿瘤细胞是否坏死的阈值，即当σ＞σD时，所有的肿瘤细胞存活；当σ≤σD时，所有的肿瘤细胞坏死.本文在前述文献［7，9-11］的基础上把 Dirichlet自由边界改为 Robin 自由边界条件下的有坏死核的非线性肿瘤生长模型进行研究，具体模型如下：

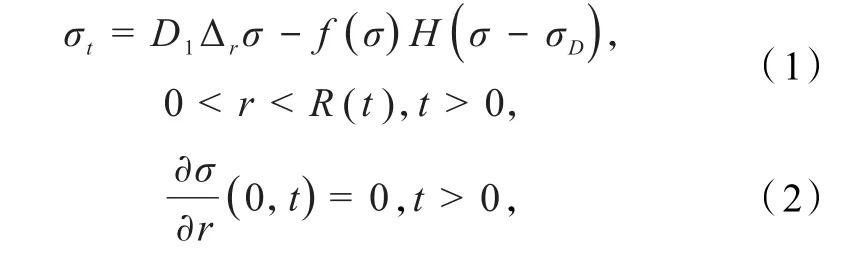
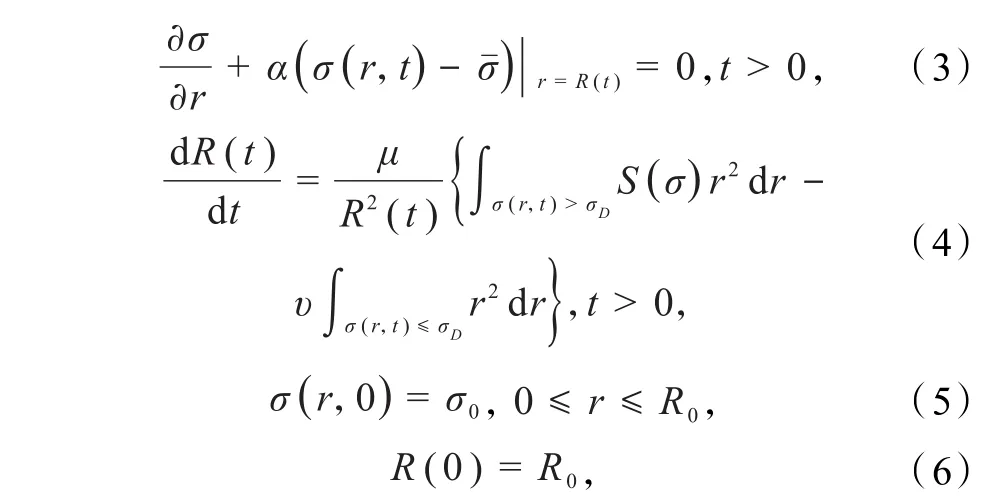
在符合生物学和医学原理的前提下，本文做出如下假设：（A1）f(σ ) =σf1(σ)，其中f1(σ)为定义在[ 0 ，∞ ]上的函数且满足Lipschitz连续，当 σ ≥0时，有f1(σ )≥0恒成立；（A2）S是定义在[0 ，∞ ]上的函数 ，且 满 足 Lipschitz 连 续 ；（A3）σ0∈ W3，∞(0，R0)，，其 中

本文对于模型中的不连续函数进行近似逼近的方法，主要是参考 Zheng 和 Cui［16］对 Dirichlet自由边界条件下的有坏死核的非线性肿瘤生长模型整体解的存在性的证明中所使用的方法，即构造光滑函数进行逼近.再结合Schauder不动点定理和抛物方程的Lp理论，最终能够得到Robin自由边界下有坏死核的非线性肿瘤模型整体解的存在性.

本文的主要结论如下：

定理 1.1 在假设（A1）、（A2）、（A3）的条件下，对于任意的T ＞0，问题（1）～（6）存在解(σ (r ， t)，R(t))，且解 σ(r ， t) 满足：

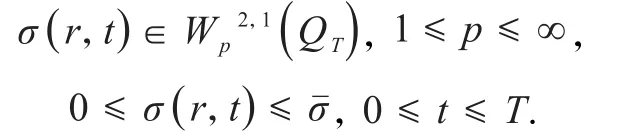
1 预备引理

2 自由边界问题的转换

3 逼近问题解的存在性

4 原模型整体解的存在性

在证明了式（21）～（24）在XT上解的存在性之后，接下来对式（1）～（6）在XT上整体解的存在性进行证明，即证明本文主要定理1.1.首先证明如下定理.

再结合式（37）和（42）可以得到

将式（42）和（43）代入式（38）～（41）中，可得式（16）～（19）存在解v=v(z ， t)，即结论得证 .

由引理2.1可知，自由边界问题式（1）～（6）与固定边界问题式（16）～（19）等价，结合定理4.1，可得式（1）～（6）整体解的存在性，即定理1.1得证.

5 结束语

本文研究了一个Robin自由边界条件下的有坏死核的非线性肿瘤生长模型，通过对模型中的不连续项进行逼近，证明了模型逼近解的存在性，从而得到原模型整体弱解的存在性.本文是用弱收敛的方法得到原模型弱解的存在性，而弱解的唯一性目前尚未得到，这是一个很困难的问题，希望将来可以找到方法得到弱解的唯一性.