基于粒子群优化在线顺序极限学习机动态环境室内定位算法
韩承毅,苏胜君,施伟斌,乐燕芬,李瑞祥
(上海理工大学光电信息与计算机工程学院,上海 200093)
引 言
在室内定位中,基于接收信号强度值(Receive signal strength,RSS)的解决方案具备成本低,易实现,精度较高等特性[1⁃3],在静态室内环境定位问题中得到广泛的运用。但是,障碍物和人员位置等室内环境因素发生变化时,基于RSS方案会导致定位误差较大等问题。如果重构指纹数据库和训练模型,会导致实验成本高、耗时长。在线顺序极限学习机(Online sequential extreme learning machine,OS⁃ELM)算法[4]适合在动态环境下进行室内定位,在变换的新环境中,只需在少量的参考点上采集新的指纹库数据信息,用来更新补充上一次训练模型的参数,就可以在新环境中进行在线估计位置信息。在室内动态环境中,该算法相比于静态室内定位算法,在定位时间上和性能上有较高的提升。但是,OS⁃ELM算法在模型输入层和隐含层之间的权重和隐含层上的偏置是随机赋值的,这就导致了隐含层输出矩阵和其转置矩阵乘法结果可能具有奇异性或者病态性[5]。当在新环境中采集的数据流发生变化时,随机赋值的权重和偏置,会导致OS⁃ELM算法隐含层输出矩阵和其转置之间的矩阵乘法结果不具有可逆解,这一缺陷导致了OS⁃ELM算法的泛化性能较差[6]。
针对此问题,本文提出了PSO⁃OS⁃ELM算法,利用粒子群优化算法(Particle swarm optimization,PSO),解决OS⁃ELM算法中输入层和隐含层权重和隐含层的偏置随机赋值问题,从而有效地控制了OS⁃ELM算法中的隐含层输出矩阵和其转置矩阵乘积为奇异矩阵或者病态矩阵的问题。本文算法继承了OS⁃ELM算法框架,引入PSO算法寻优环节,且解决了以下3点问题:(1)解决了RSS的时变性问题;(2)解决了OS⁃ELM算法隐含层输出矩阵和其转置乘法结果可能为奇异矩阵或者病态矩阵的问题;(3)解决了定位算法耗时长问题。
1 算法的框架与原理
针对动态室内定位环境问题,Yang等[7]利用在线顺序极限学习机方法,在新环境中采集新数据来更新调节模型参数,有效降低了在动态变化环境中重复大规模采集数据的成本,能够自动及时适应环境变化,算法收敛速度较快,具有较高的定位精度。但是OS⁃ELM算法中输入层到隐含层之间的输入权重和隐含层阈值的随机性,导致了算法的鲁棒性并不很好[8]。
1.1 OS‑ELM算法
极限学习机(Extreme learning machine,ELM)是一种单隐层前馈神经网络架构[9],在ELM模型之上引入在线顺序机制,就形成OS⁃ELM网络模型。OS⁃ELM网络模型由输入层、隐含层、输出层构建形成,整个网络模型如图1所示。在图1中,为第j次采集数据且来自于第d个AP的信号强度,w i为隐含层第i个神经元与输入层所有神经元连接的权重,为隐含层第i个神经元与输入层第j个神经元连接的权重,b i为隐含层第i个神经元的阈值大小,g(∙)为隐含层神经元的激活函数,βi为隐含层第i个神经元与输出神经元之间的权重为第j次输出层的第k个维度的数值,L为隐含层神经元的个数;OS⁃ELM算法分为初始化阶段和在线学习阶段。

图1 OS-ELM算法网络模型Fig.1 OS-ELM algorithm network model
(1)初始化阶段
步骤1输入权重w i和阈值b i在[-1,1]范围内等概率地随机赋值,i=1,2,…,L。
步骤2计算隐含层初始输出矩阵H0,是一个N0维L列向量。
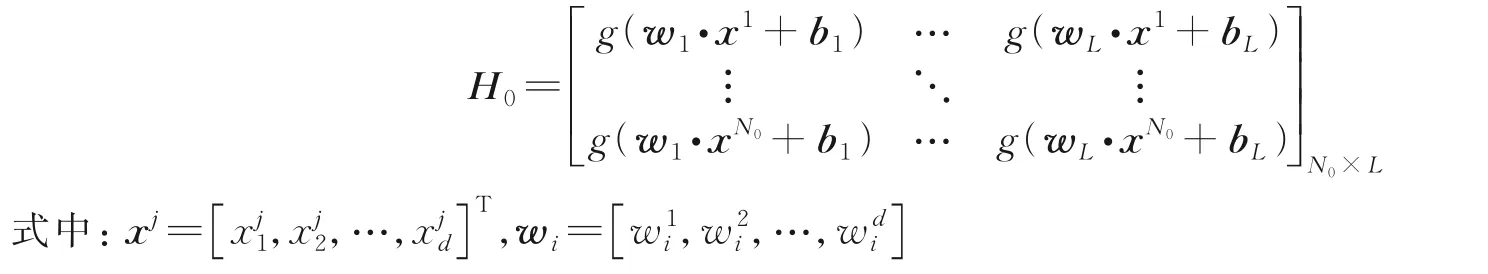
步骤3 计算初始输出权重
整个网络模型可写为
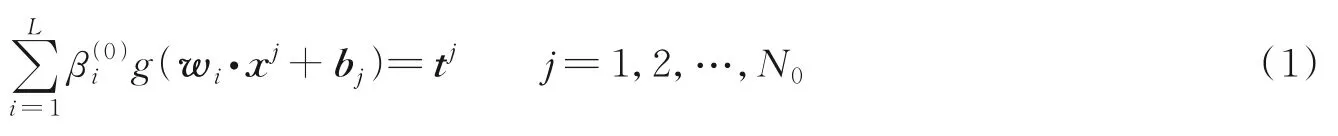
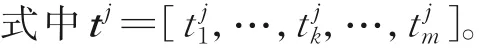
式(1)可以简写为

式中
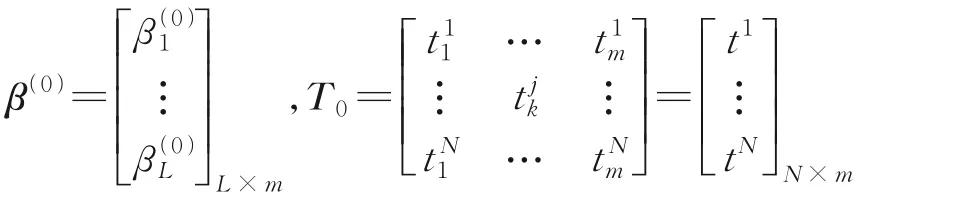
整个问题就等价于式(3)。

式中H0代表着初始时刻系统矩阵。由于OS⁃ELM算法中的输入权重和隐含层输入阈值是随机赋值的,这就导致矩阵HT0H0可能是不可逆矩阵或者是病态矩阵。如果矩阵HT0H0可逆[10],那么β(0)=P0HT0T0,其中P0=(HT0H0)-1,记K0为初始时刻P0的逆矩阵参数
步骤4设置k=0,k表示数据采集的次数。
(2)顺序学习阶段
当环境发生变化时,就需要在新环境中采集新数据集。
设定第k+1次采集的新数据集为
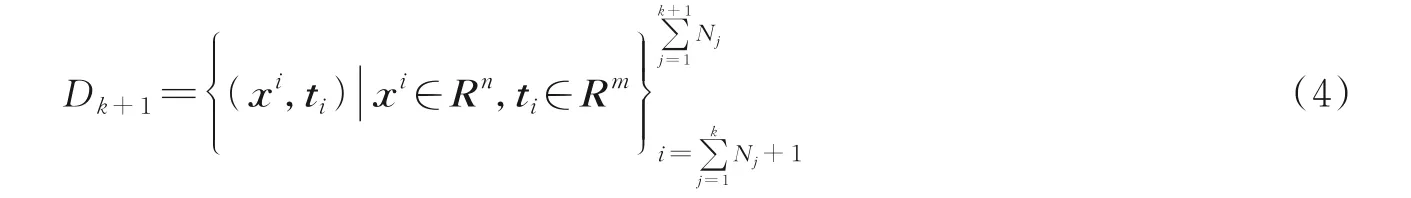
式中N j为第j次采集RSS数据集的大小。
步骤1隐含层输出矩阵H k+1
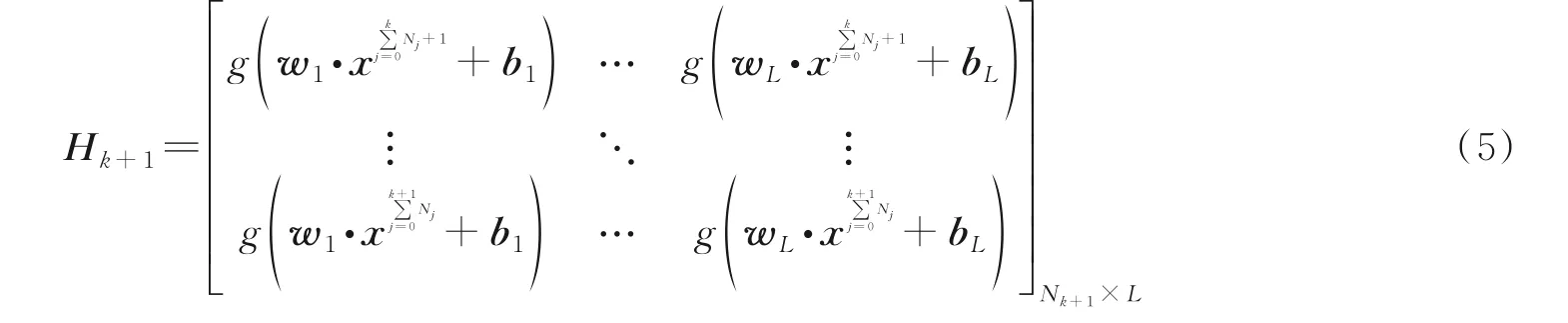
式中H k+1为第k+1次隐含层神经元输出结果,由新环境下采集到的锚节点信号强度数据计算得出。
步骤2隐含层到输出层之间的权重β(k+1)
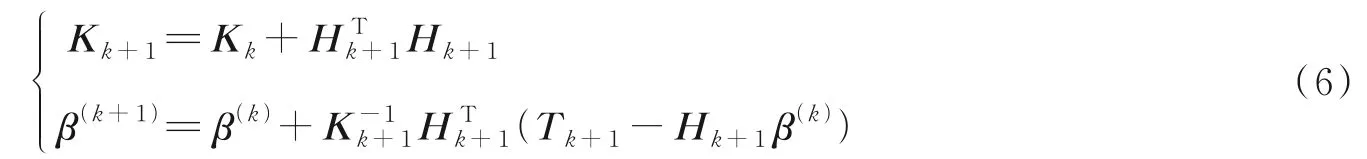
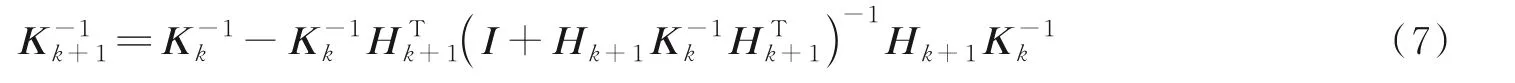
将式(6)转换为式(8),有
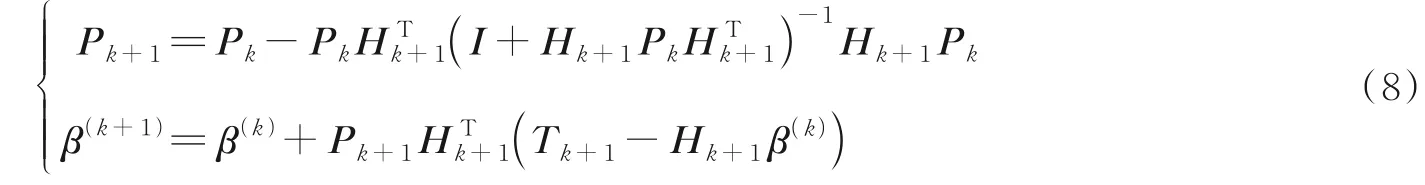
步骤3k=k+1返回顺序学习阶段。
1.2 PSO‑OS‑ELM算法
Han等[11]指出OS⁃ELM算法中输入权重w和隐含层阈值b是随机赋值,矩阵HTH可能出现病态矩阵,导致整个算法鲁棒性较差。根据文献[12⁃15]可知,矩阵的条件数是可以作为判断矩阵是否病态的一种度量。条件数越大,矩阵越病态。矩阵H的条件数可以写为

式中:λmax(HTH)为矩阵HTH的最大特征值,λmin(HTH)为矩阵HTH的最小特征值。当HTH的条件数越小时,说明HTH病态性越小,模型的鲁棒性越强,模型的误差越小。本文PSO算法中的矩阵H的条件数K2(H)作为寻找OS⁃ELM算法中输入层和隐含层之间的权重w和隐含层偏置b的最优值准则,使算法鲁棒性更强、计算耗时少、定位误差小。PSO⁃OS⁃ELM算法流程如图2所示。
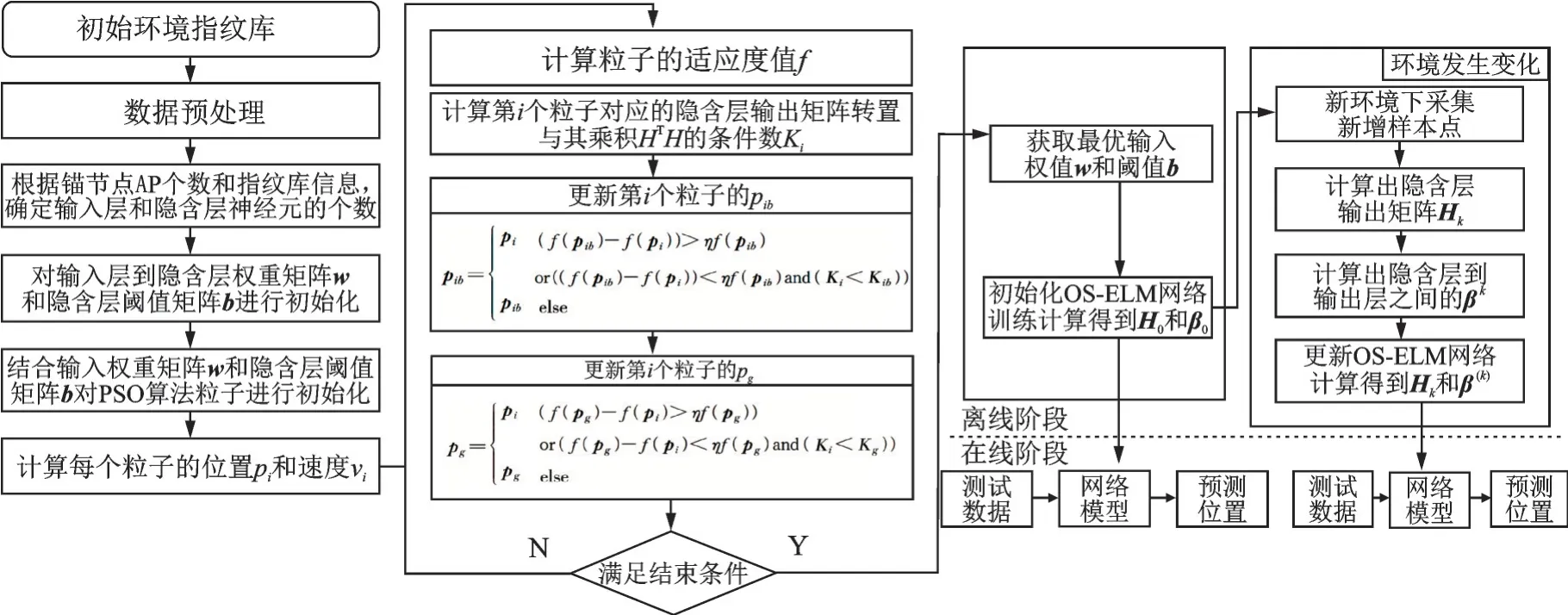
图2 PSO-OS-ELM算法框Fig.2 Schematic diagram of PSO-OS-ELM algorithm
步骤1初始化算法中相关参数
PSO算法中的粒子代表着OS⁃ELM算法中的输入层权重w和隐含层阈值b的可行解,即粒子p i=[w1,…,w L,b1,…,b L],每次粒子都有其对应的最优解p ib。f(x)为适应度函数,在本实验中f(x)=其中t为参考点的实际位置。
步骤2更新每个粒子的局部最优解p ib
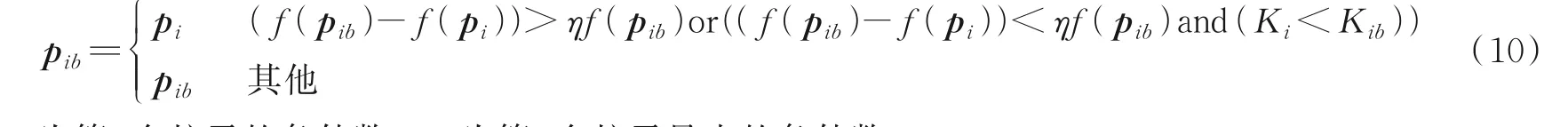
式中K i为第i个粒子的条件数,K ib为第i个粒子最小的条件数。
步骤3更新全局最优解p g
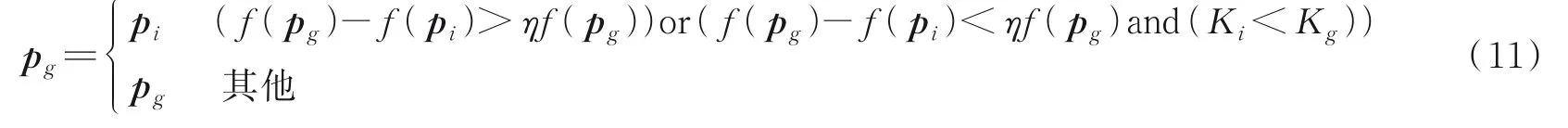
式中K g为全局最小的条件数。
在PSO算法迭代更新p ib、p g中,式(9,10)引入矩阵条件f(p ib)-f(p i)<ηf(p ib)、(K i 步骤4根据式(11,12)更新粒子的速度和位置。 式中:i=1,2,…,D,D为粒子的总个数;c1、c2为学习因子;r1、r2为[-1,1]范围内的随机数;α为约束因子,控制位置更迭速度;vi为第i个粒子的速度;λ为惯性因子,为非负数,当该值较大,全局寻优能力强,局部寻优能力弱;当该值较小,全局寻优能力弱,局部寻优能力强。 步骤5未达到一定的迭代次数或未满足一定的误差范围,则跳转到步骤(2)。 步骤6达到结束条件,执行OS⁃ELM算法流程,在不同的环境中,采集新的数据,按照式(7)进行迭代更新计算。 为评估本文提出的PSO⁃OS⁃ELM算法的性能,实验将算法分别同OS⁃ELM算法和加权K近邻算法(Weighted K⁃nearest neighbor,WKNN)算法作对比,评估定位精度、算法耗时和鲁棒性等指标。 本次实验场地为上海理工大学光电楼9楼实验楼,实验场地的形状为矩形,其面积为14 m×58 m。图3中,红色三角形标记为锚节点,负责发送信号,在整个实验场地两侧共分布了13×2个AP节点,每个锚节点间隔4.8 m;黑色方形为测试节点;蓝色圆圈为参考节点;红色圆圈为重新采集点的位置;阴影区域为墙壁或办公室区域。在不同时间段下,整个实验场景的空间环境不同、信号强度不同。在大多数的工作日下午的时间段,人员随机走动或休憩,信号容易受到干扰;在大多数的工作日晚上时间段,人员稀少,空间十分空旷,障碍物少,信号强度一般较好;在非工作日的上午,实验场地障碍物分布较多,信号强度会受到干扰衰减。 图3 实验平面实验图Fig.3 Schematic diagram of experimental area 本次实验将整个实验环境划分为3个主要时间段:(1)工作日晚上时间段,无人无障碍物环境;(2)工作日下午时间段,有人无障碍物环境;(3)非工作日上午时间段,有人有障碍物环境。 将CC2530开发板设备放置于蓝色参考点上,在3种不同环境中沿着图3黑色虚线移动,收集到26个AP节点信号强度值。在同一位置多次接收的信号进行数值处理后作为信号强度值,和参考点坐标同时记录在离线阶段的数据指纹库中。实验中未接收到的RSS信号强度统一用最小值90 dBm填充。由于接收信号强度的不稳定性,在每个测试点上进行反复测试100次,然后对接收的信号求平均值,作为该点的信号强度值。在顺序学习阶段中,在图3中的红色圆圈中的位置重新采集RSS信号,每个点采集300次,构建一个新的信号强度数据集,避免了重复测量全部点。 利用3种环境中采集到的数据,将本文提出的PSO⁃OS⁃ELM算法与OS⁃ELM算法、WKNN算法(加权K近邻算法)进行对比分析。本实验中,经对WKNN算法的K参数大量调优后,当K为4时算法定位精度最佳,故将K取为4。实验采用平均定位误差(Mean error,ME)、定位算法耗时、定位误差的累计密度函数(Cumulative density function,CDF)作为标准来评估算法的性能。 由表1可知,在无人无障碍物情况下,PSO⁃OS⁃ELM算法定位误差相较于OS⁃ELM算法减少了11.1%、相较于WKNN算法减少了8.48%;在有人无障碍物,PSO⁃OS⁃ELM算法定位误差相较于OS⁃ELM算法减少了19.4%,相较于WKNN算法减少了24.34%。有人有障碍物的环境下,PSO⁃OS⁃ELM算法定位误差相较于OS⁃ELM算法减少了27.5%,相较于WKNN算法减少了33.95%。PSO粒子群优化算法确保了OS⁃ELM算法的鲁棒性,削弱了动态环境因素对定位精度的影响。 表1 3种算法在3种不同环境下的平均定位误差Table 1 Average positioning error of three algorithms in three different environments m 由表2可知,从算法耗时角度来看,在3种环境下,虽然PSO⁃OS⁃ELM算法引入了粒子群算法,但与OS⁃ELM耗时相当,说明粒子群算法的时间复杂度比较小。从WKNN算法的耗时长来看,说明了在动态变化的室内环境中,与重新构建指纹库训练预测的方法相比,在线顺序学习更新的方法能够有效减少计算和提高定位算法效率。PSO⁃OS⁃ELM算法继承了OS⁃ELM算法耗时短的特点,算法耗时相较于传统定位算法WKNN算法减少了55%左右。 表2 3种算法在3种不同环境下的定位算法耗时Table 2 Time consuming of three algorithms in three different envir onments s 在3种环境下,记录PSO⁃OS⁃ELM算法和OS⁃ELM算法中的隐含层神经元输出的矩阵H的条件数K2(H)的最大值,如表3所示。可以发现在环境发生变化的情况下,PSO算法可以有效地减小条件数K2(H),使输入层到隐含层的权值处于最佳值。结合图4,可以发现PSO⁃OS⁃ELM算法相较于OS⁃ELM算法,更有效地控制定位误差,说明算法在动态变化的环境中鲁棒性更强。 表3 在3种不同环境下K 2(H)的最大值Table 3 The max value of K 2(H)in three different envir onments 从图4可知,在每种环境中,PSO⁃OS⁃ELM算法在误差1~1.8 m范围内,误差累积分布就达到90%,说明PSO⁃OS⁃ELM算法的定位误差更小;同时,与传统的WKNN算法相比,通过迭代和更新方式比重建训练方式更加高效和快速,大大减少训练的时间。通过图4(a,b)可知,在3次动态变换的环境中,PSO⁃OS⁃ELM算法相较于OS⁃ELM算法,定位误差累积分布曲线更加趋同性,能根据外界变化的环境不断更新调整算法中输入层和隐含层权重和隐含层的偏置数值,确保定位误差变小,说明算法在动态变化的环境中鲁棒性更强。 图4 3种算法在3种环境中误差累积分布函数图Fig.4 Cumulative distribution function of positioning error about three algorithms in three environments 本文利用PSO算法寻找OS⁃ELM算法中输入层和隐含层之间的权重w和隐含层偏置b的最优值,有效地解决OS⁃ELM算法中的隐含层输出矩阵和其转置矩阵乘法结果可能为奇异矩阵或者病态矩阵的问题,使算法鲁棒性更强、计算耗时少且定位误差小。通过实验结果分析,在有限空间的无人无障碍物、有人无障碍物和有人有障碍物情况下,同WKNN算法相比,PSO⁃OS⁃ELM算法定位误差分别减少了8.48%、24.34%和33.95%;同OS⁃ELM算法相比,PSO⁃OS⁃ELM算法保持较好的鲁棒性,并且很好地继承了OS⁃ELM算法的泛化能力和较强的非线性逼近特性。本实验还未针对更大区域范围内的动态变化室内环境进行定位实验,这也是本算法的下一阶段研究分析目标。
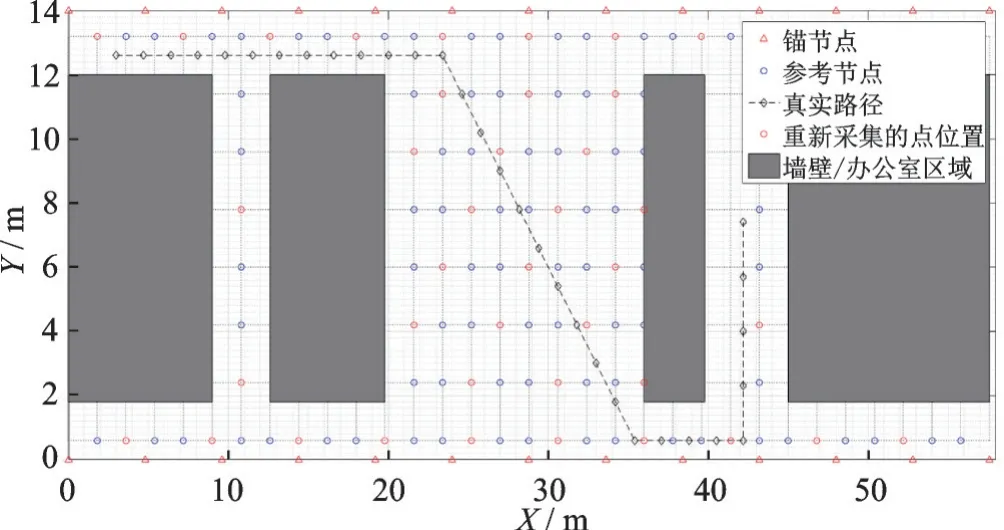
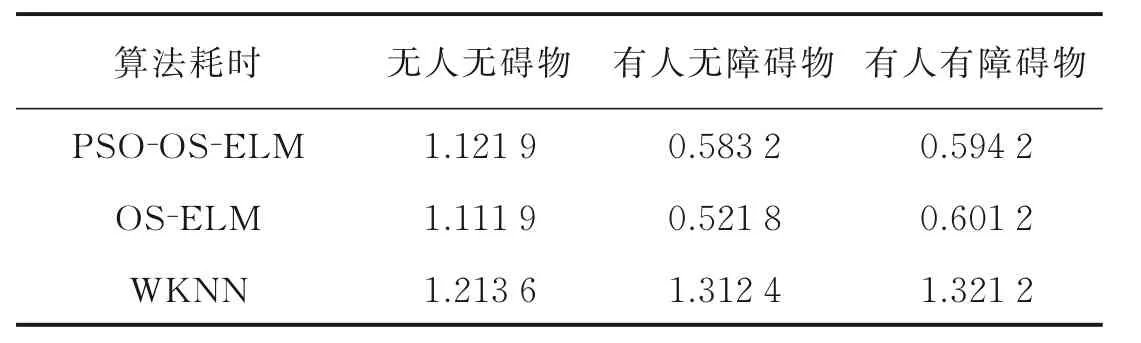
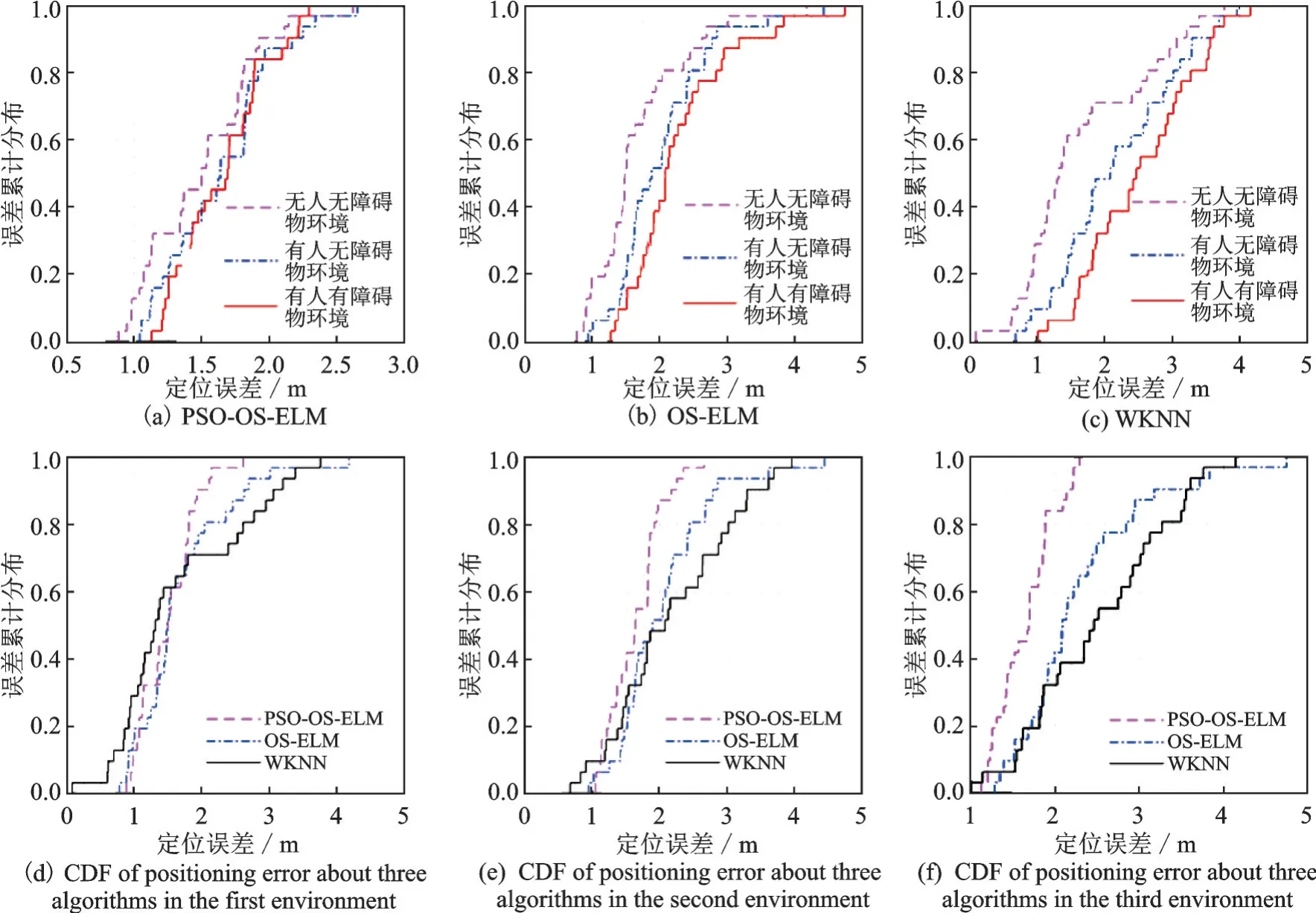
2 实验结果及分析


3 结束语

