基于TRIAA与压缩感知的ISAR去微多普勒方法
张荣政,王 勇
(哈尔滨工业大学电子工程技术研究所,哈尔滨 150001)
引 言
随着雷达技术的发展,雷达的信号质量和分辨率逐渐提升,传统逆合成孔径雷达(Inverse synthesis aperture radar,ISAR)成像技术已无法满足清晰化、精细化的成像需求。转台成像模型通常假设所有的散射点都随目标整体一起运动,但是ISAR成像的常见目标上经常有些独立运动的部件,例如飞机的螺旋桨叶片。这些部件相对于目标整体高速旋转,造成了回波多普勒谱的展宽,形成了所谓的微多普勒效应[1‑4]。若直接采用传统的ISAR成像算法,由旋转部件造成的多普勒谱展宽会在成像结果上形成条带干扰,从而影响成像质量。
针对这一问题,有一类解决方法是在成像前预先从回波中分离由刚体散射点形成的信号和由高速旋转散射点形成的信号。文献[5]提出一种基于低调频率匹配滤波的信号分离方法,用搜索的方式挑选出有效的刚体信号。文献[6]提出了一种基于多重测量矢量(Multiple measurement vectors,MMV)和压缩感知(Compressive sensing,CS)的含旋转部件目标ISAR成像方法,根据刚体与旋转部件信号的MMV模型稀疏性的不同分离信号。文献[7]使用Radon‑Wigner变换方法对信号的Wigner‑Ville分布进行直线线积分,以此识别散射点类型,再利用CLEAN技术完成了信号分离。文献[8]利用复数局部均值分解将复杂信号分解成若干个单分量信号,从而分离出微多普勒信号。
另一类方法是将微多普勒信号视作干扰直接滤除,再进行ISAR成像。文献[9]提出了一种基于短时傅里叶变换(Short‑time Fourier transform,STFT)时频分布和L‑统计量的ISAR成像去除微多普勒效应方法,该方法利用刚体和旋转散射点时频特征的不同,从时频图上删除代表旋转部件那部分元素,再将处理后的时频图还原成信号并完成ISAR成像。文献[10]利用时间递归迭代自适应方法(Time re‑cursive iterative adaptive approach,TRIAA)[11‑12]替换原方法的STFT时频分析,从而提高了时频分析的分辨率,更有效地去除了微多普勒效应。文献[13‑15]中,压缩感知技术被用于信号还原过程,从而在原方法基础上提升了成像质量。
本文基于上述研究工作,首先利用TRIAA提高时频分析的频率分辨率,从而更有效去除干扰,再使用压缩感知稀疏重构技术还原去除干扰后的信号,最终提出了一种基于TRIAA和压缩感知的ISAR成像去除微多普勒效应方法,在原方法基础上提高了ISAR成像质量。
1 含旋转部件的ISAR信号模型
ISAR系统通常采用发射线性调频信号再用Dechirp处理的方式提高发射信号的带宽,从而增加距离分辨率。设载频为fc,脉冲重复时间为T,雷达信号的发射时刻就是tm=mT,m=0,1,2,…,于是发射信号就可以表示为
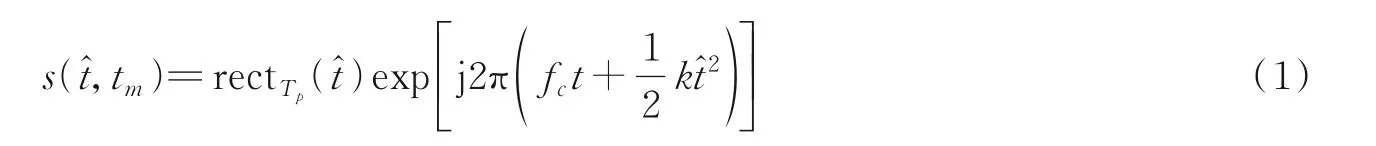
式中:rectT p(u)表示长度为T p的矩形窗,t̂表示脉冲内的快时间,k表示调频率,c表示电磁波传播速度。假设tm时刻第i个散射点距离雷达的相对距离是Ri(tm),回波就可以表示为
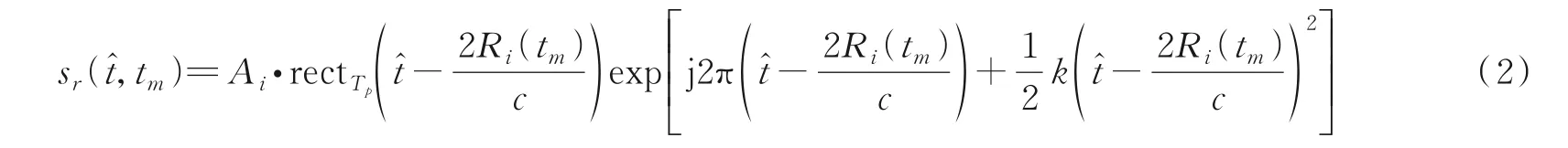
式中A i表示每个散射点的回波强度。经过Dechirp处理以及脉冲压缩,雷达信号转化为
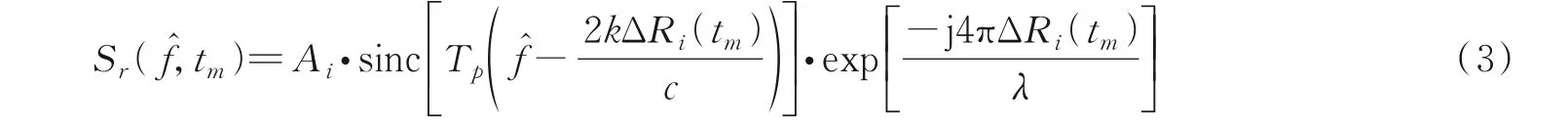
式中:λ表示发射信号的波长,ΔRi(tm)表示每个散射点与成像参考点的瞬时距离。假设运动补偿已经完成且散射点跨域距离单元的问题可以忽略,距离单元内的每个散射点对应的信号可以表示为
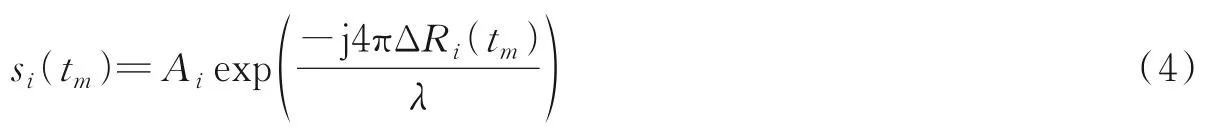
接下来,分析含有高速旋转部件的距离单元内信号的具体形式。图1给出了含旋转散射点的ISAR几何模型,这里平动补偿已经完成,目标整体绕O点转动构成转台模型。某一距离单元内有刚体散射点A以及高速旋转散射点B,A随目标整体以角速度ω0转动,B除了随目标整体的运动外,还绕B以角速度ωs高速转动。OA和AB在初始时刻与OX轴的夹角分别为θA和θB。
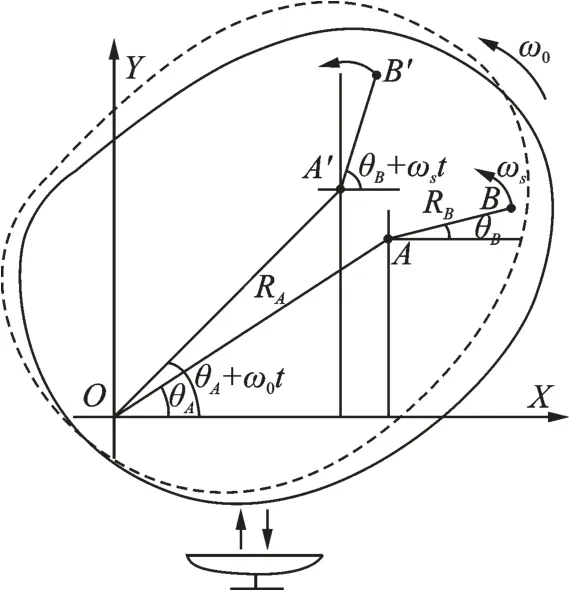
图1 含有旋转散射点的ISAR几何模型Fig.1 ISAR imaging model with rotat‑ing parts
所以散射点A与参考点的距离为
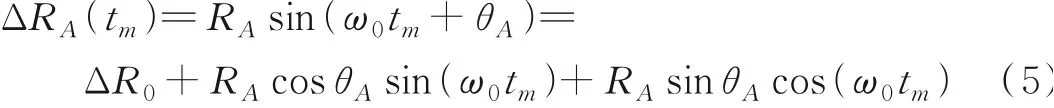
式中ΔR0为转台原点O到参考点的距离。由于成像时间内,目标 整 体 的 旋 转 角 度ω0tm非 常 小,因 此sin(ω0tm)≈ω0tm,cos(ω0tm)≈1。代入式(5),A在距离单元内的信号可表示为
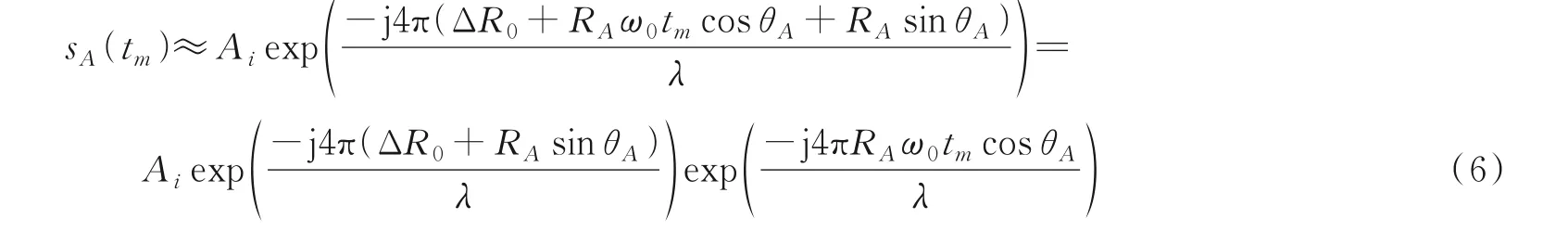
sA(tm)显然是一个单频信号,下面用同样的方法可以得到散射点B到参考点的距离为

同理,可得B在距离单元内的信号可表示为
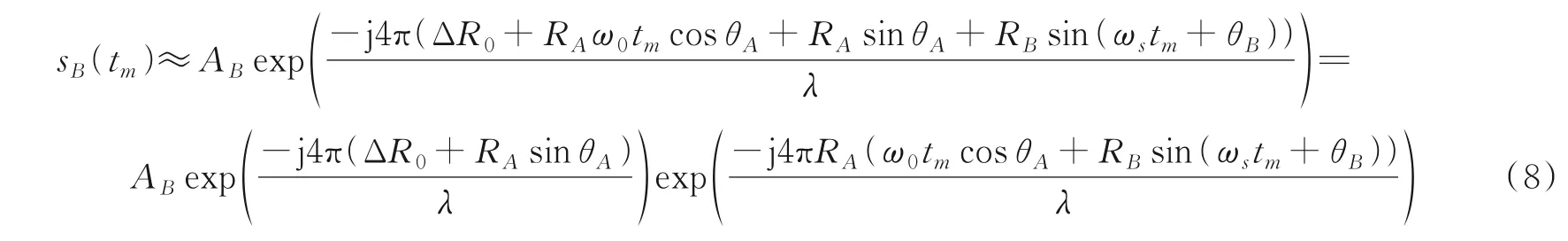
接下来考察信号sB(tm)的频率,可以得到

于是,发现旋转散射点B的多普勒频率以正弦形式变化,所以旋转散射点对应的信号为正弦调频信号,这就是所谓的微多普勒效应。而如式(6)所示,随目标整体运动的散射点A对应单频信号,因此将信号转换到频谱就能将A的信号压缩为一个独立的点,这就是距离多普勒方法(RD)成像的基本原理。但是假如距离单元内同时存在高速旋转散射点B,其对应的正弦调频信号会在成像结果上形成条带干扰。
2 时间递归迭代自适应以及压缩感知的微多普勒效应去除方法
根据第1节的介绍可知旋转部件会引起微多普勒效应,处理微多普勒效应的第一步是时频分析,文献[9]采用了STFT时频分析。文献[10]利用TRIAA得到了更清晰的时频分布,又利用刚体散射点与旋转体散射点信号时频特征的区别,剔除了含有旋转体散射点信号的元素。本文采用压缩感知方法将处理后的时频分布还原成信号频谱,直接得到了ISAR结果。
2.1 时间递归迭代自适应方法
对于一个距离单元内的离散信号x(n),n=1,2,…,N,可以用滑窗分割的方式将其分段为
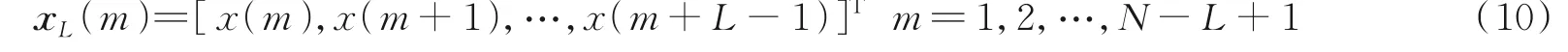
这里窗长为L,因此一共分成了M=N-L+1段。接下来根据窗长设置频率导向矢量
这里ωk=2πk/K,k=0,1,…,K-1,K表示频率采样点数,一般K>L。α(ωk)表示sL(m)在频率ωk处的复振幅,其协方差矩阵R就可以写成

式中|α(ωk)|2表示信号在频率ωk的功率。接下来,采用加权最小二乘估计来估计复振幅α(ωk)。首先构造优化问题
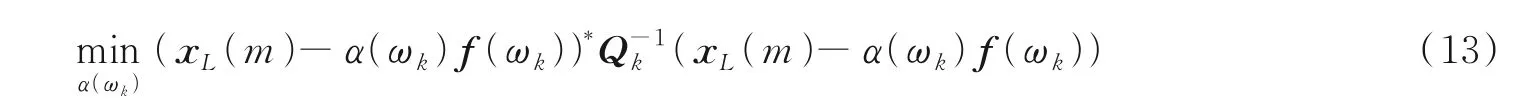
式中Q k=R-|α(ωk)|2f(ωk)f*(ωk)表示广义噪声协方差矩阵,其物理意义在于假设信号在频率ωk处的复振幅是α(ωk),把信号中除频率ωk外成分都视为噪声,因此当估计复振幅时加权矩阵应取Q-1k。当加权的剩余平方和最小时,就得到了复振幅的估计值。具体细节可参考文献[16‑17]。代入最小二乘估计解的一般形式,该优化问题的最优解为

应用矩阵求逆引理,最终式(14)简化为

通过以上推导可以看出,首先设|α(ωk)|2=1,k=1,2,…,K,代入式(12)和式(15)得到初步结果再将结果代回式(12)和式(15)并反复迭代多次,即可得到x L(m)的频谱对滑窗分割形成的每一段数据进行同样处理,就能观察到x(n)的频谱随时间变化的情况,这就是TRI‑AA的基本原理。考虑到相邻窗之间,如x L(m)和x L(m+1)之间的频谱差别不大,因此就能将前一段的结果作为下一段的迭代初始值,从而极大减少迭代次数。
TRIAA的具体步骤如下:
步骤1将数据s(n)用滑窗的方式分段,每段数据的具体形式参考式(10),于是得到下列矩阵
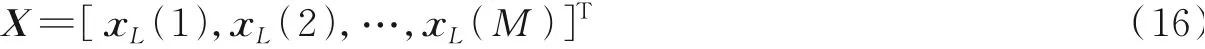
步骤2设|α(ωk)|2=1,k=1,2,…,K,将x L(1)代入式(12)和式(15),得到初步结果再将和x L(1)代 回 式(12)和 式(15)并 反 复 迭 代 多 次,即 可 得 到x L(1)的 频 谱
步骤3设将x L(2)代入式(12)和式(15),得到x L(2)的频谱并以此类推,设将x L(m)代入式(12)和式(15),即可得到x L(m)的频谱一直计算到x L(M)。
步骤4将每段数据的频谱拼接为一个矩阵,结果就是用TRIAA方法获得的时频分布
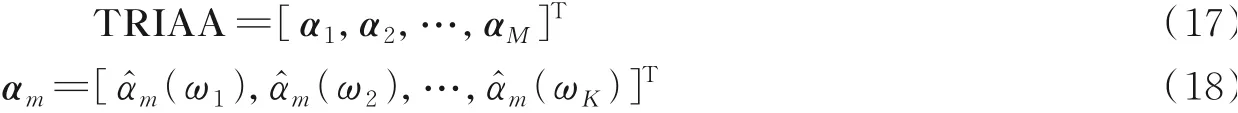
2.2 基于TRIAA和压缩感知的微多普勒消除方法
假 设 待 处 理 的 信 号 是x(n),n=1,2,…,N,其 离 散 傅 里 叶 变 换 就 可 以 表 示 为X(k),k=1,2,…,K。对其进行TRIAA时频分析,根据式(17)和式(18),TRIAA上每个元素可表示为

根据式(15),R m为直接得到(ωk)的协方差矩阵,则有如下形式

这里

于是,某个时刻m的瞬时频谱可以表示为
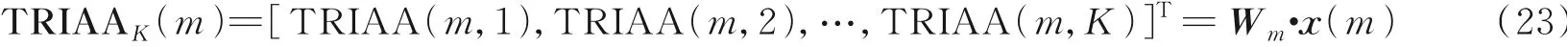
式中

这样,整个TRIAA过程就可以表示为

这里向量x表示完整的时域信号

TRIAA表示大小为M×K的矩阵,即

而KM×N维的系数矩阵W可以表示为
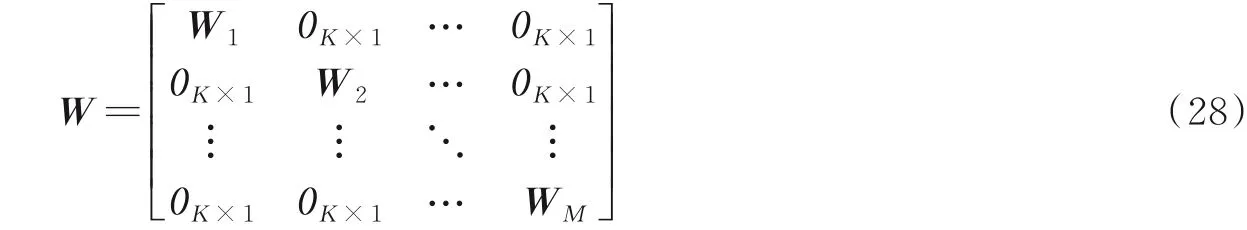
这里0K×1表示元素全为零的列向量。由于TRIAA采用滑窗形式,因此W1,W2,…也以同样的滑窗形式分布。然后,用表示傅里叶逆变换矩阵,代入式(25)就有以下关系
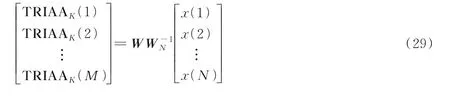
设X为x的傅里叶变换,最终获得如下关系

对于信号x(n)的短时傅里叶变换TRIAA(m,k),把频率为ωk的元素都放在同一个集合Xk(m)里,有
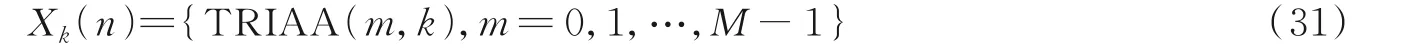
然后计算集合X k(m)所有元素的绝对值,并根据绝对值的大小将所有元素从小到大重新排列,得到新集 合ψk(m)∈Xk(m),满 足|ψk(0)|≤|ψk(1)|≤|ψk(2)|≤…≤|ψk(M-1)|。时 频 图 上 的 单 频 信 号 由 于频率不随时间改变,因此重排后顺序几乎不变。而如正弦调频信号的非平稳信号频率随时间改变,所以其元素会下沉到绝对值较大的一侧。
接下来,设置一个门限Q,剔除ψk(m)绝对值较大的那部分元素,若M Q=int[M(1-Q/100)]表示剩余的元素个数,M-M Q表示从ψk(m)中剔除的元素个数。根据第1节对距离单元内信号的分析可知,高速旋转散射点对应正弦调频信号,刚体散射点对应单频信号。于是经过此番处理,TRIAA上剩余的元素就只包含了刚体散射点产生单频信号。
然而,正弦调频信号和单频信号可能会发生重叠,这就造成了在时频图上剔除正弦调频信号时也可能损失一部分单频信号。考虑到ISAR成像时,目标一般满足散射点模型,每个距离单元内的刚体散射点的个数也为有限个。每个散射点又只对应一个单频信号,所以滤除正弦调频分量后的信号在频域上有稀疏性。因此依据式(30),滤除正弦调频分量后的TRIAA可用压缩感知方式直接还原为滤除正弦调频分量后信号的频谱X′。这样也直接完成了ISAR成像的最后一步,既方位向压缩。
令TRIAACS表示删除含干扰元素后的TRIAA,再省略AFULL上对应的行,就得到恢复矩阵ACS,并且满足如下关系

因此,得到如下最小化问题

解决该最小化问题,即可得到滤除正弦调频分量后信号的频谱X′。而由于TRIAACS上已无含有干扰的元素,所以频谱X′只包含刚体信号。
对于消除的比例Q,有两种设定的方法。第一种选择是设置一个固定的消除百分比,只要消除比例Q足够大,可以消除所有范围内的干扰。当微多普勒效应所占能量较大时,所需的Q也较大。当计算时频分布的窗口长度较长时,正弦调频信号的频率在每个窗口内变化很大,导致时频聚集性变低,所需的Q也更大。
另一种更复杂的方法是为每个距离单元中的信号设置自适应的消除百分比[9],其原理是当信号的时频分布重新排列后,包含微多普勒效应的部分比只包含单频信号的部分能量增加更大。然而,该方法要求信号的微多普勒效应引起的频带扩展足够大,且信号的信噪比足够低。
最终信号分离方法的具体步骤如下:
步骤1计算信号的TRIAA,在计算m时刻的频谱时,记录对应的协方差矩阵R m。
步骤2根据TRIAA上每个元素的绝对值大小沿时间重排。设置门限,剔除绝对值大的那部分元素,从而得到TRIAACS。
步骤3用记录下来的R m,构造矩阵W。计算再根据TRIAACS构造恢复矩阵ACS。
步骤4解决式(33)中的最小化问题,得到去除干扰后信号的频谱。
3 实验与分析
3.1 仿真信号分离
首先用仿真信号实验展示本文的信号分离方法。仿真一个多个单频分量和多个正弦调频分量组成的信号

3个单频信号的频率分别为50、30和10 Hz;两个正弦调频信号的调频率都是90,重复频率分别为1.5和1 Hz,信号的采样点数为256,这里设置采样频率为1 Hz,信噪比为20 dB。信号分离的过程如图2所示。

图2 基于TRIAA和压缩感知的信号分离实验Fig.2 Signal separation experiment based on TRIAA and compressive sensing
图2(a)表示信号由TRIAA得到的时频图,可以在图中看到3条直线和2条正弦曲线,分别表示单频信号和正弦调频信号。图2(b)表示将时频图按每个元素绝对值的大小沿时间维重新排列后的结果。图2(c)黑色的部分就是含有干扰元素的位置,这里将去除门限设置在60%。图2(d)表示剔除干扰信号后的时频图。
然后就能用正交匹配追踪恢复清除干扰后信号的频谱。这里对比本文方法与文献[9]中基于ST‑FT的信号分离方法。恢复的频谱结果如图3所示。图3(a)表示使用文献[9]中的信号分离方法的结果,可见得到的频谱仍然包含部分干扰。图3(b)表示利用本文方法重构后的信号。可见本文方法的频谱干扰几乎全部被剔除。另外,3个单频信号的幅度应该是相近的,而图3(a)3个峰出现明显区别,这说明有效信号在处理中发生了损失。从图3(b)可见本文方法的信号损失要小很多,这说明压缩感知方法可以更好地恢复信号。
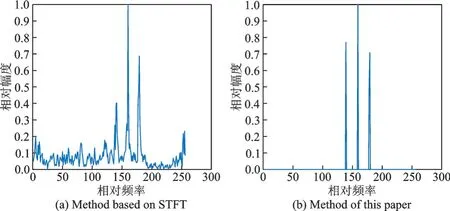
图3 信号分离结果Fig.3 Signal separation results
3.2 实测数据ISAR成像实验
接下来,将本文方法应用于实测的雷达回波。具体流程图如4所示。

图4 本文方法ISAR成像流程图Fig.4 Flow chart of ISAR imaging
为了验证所提方法的有效性,使用本方法对含有微多普勒干扰的飞机实测数据进行ISAR成像实验。这里,雷达载频为5 520 MHz,带宽为400 MHz,脉冲重复频率为400 Hz。飞机两侧机翼有一对螺旋桨,可见两条明显的条带干扰。常规RD算法的成像结果如图5所示。
图5表示An‑26飞机的RD成像结果,可以看到图上有两条严重的条带干扰,这是由于两个螺旋桨的旋转形成的微多普勒效应。然后使用文献[9]方法以及本文方法来处理干扰最显著的第65个距离单元内的信号。实验结果如图6所示。

图5 An‑26飞机RD成像Fig.5 RD imaging of An‑26
图6(a)表示对第65距离单元内的信号使用FFT进行方位向压缩后的结果,可以发现微多普勒效应形成的频带展宽。图6(b)展示了使用文献[9]的基于STFT方法消除干扰后的频谱,这里将去除门限设置在50%,可见该方法消除了大部分干扰,但是部分干扰仍然存在。图6(c)表示使用本文方法后的处理结果,可见干扰几乎全部被滤除。接下来处理全部距离单元,成像结果如图7所示。
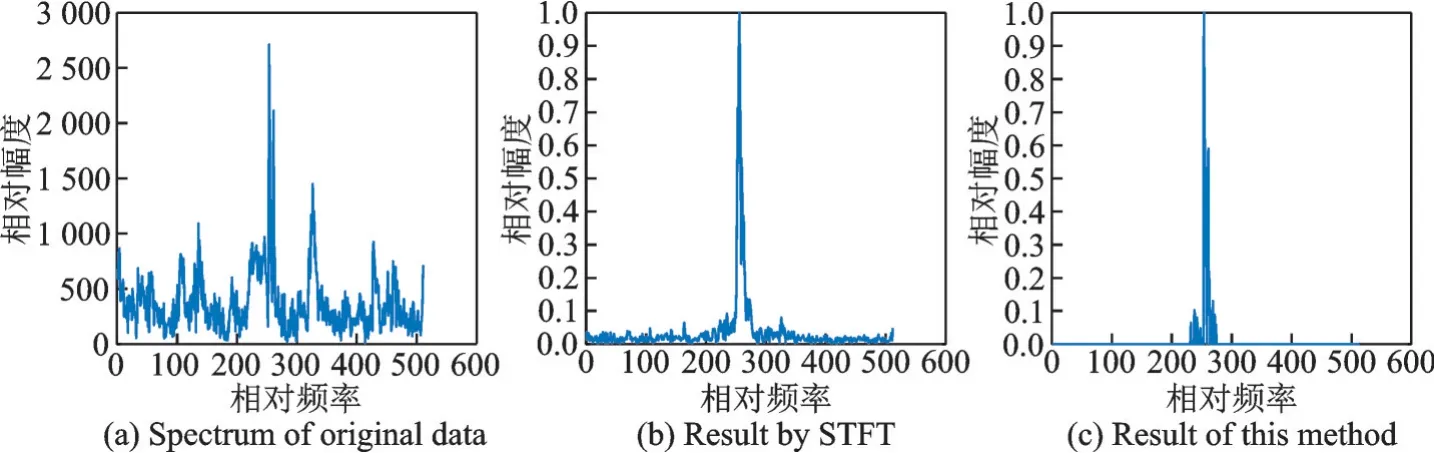
图6 第65个距离单元中的信号Fig.6 Signal in the 65th range cell

图7 An‑26飞机去微多普勒ISAR成像Fig.7 An‑26 aircraft filtered micro‑Doppler ISAR imaging
图7(a)表示利用文献[9]中的基于STFT方法的ISAR成像结果,可见大部分条带干扰被消除。图7(b)表示使用本文方法去除微多普勒效应的ISAR成像结果,可见本方法基本完全消除了微多普勒效应造成的干扰,且飞机目标的轮廓清晰,效果明显优于文献[9]中的方法。最后,用成像结果的图像熵对比这两种方法的效果。图像熵越小说明干扰越少,图像越清晰。基于STFT的方法得到的图像熵是6.365 9,而基于TRIAA和压缩感知方法的图像熵是4.778。这表明本文方法的成像效果最好。
4 结束语
ISAR成像的目标上经常存在螺旋桨叶片等高速运动散射点,这些部件形成的微多普勒效应会在成像结果上形成条带干扰,从而影响成像质量。本文提出了一种基于TRIAA和压缩感知技术的ISAR成像去微多普勒方法。仿真和实测数据的实验结果验证了本文方法的有效性。

