基于混沌与Wigner谱的探干一体化波形设计
陈义源,汪 飞,陈 军,周建江
(1.南京航空航天大学雷达成像与微波光子教育部重点实验室,南京 211106;2.南京信息工程大学电子与信息工程学院,南京 210044)
引 言
随着无源探测系统技术的快速提升,雷达面临的射频暴露威胁不断增大。射频隐身波形设计是实现雷达射频隐身的关键途径。这类波形设计的实质是在满足雷达性能需求和适应实战任务条件的前提下,设计具有峰值辐射功率低、波形时域不确定性大的雷达发射波形[1]。其中,设计探测和干扰功能一体的发射波形是利用该波形的类干扰特性进行隐蔽探测,使敌方无源探测设备误以为截获的信号仅为干扰信号,因而具备优良的射频隐身性能。
随机信号与噪声雷达信号是探干一体化波形的重要表现形式,国内外学者已开展大量研究。张勇等[2]利用单向耦合映象格子生成时空混沌二相序列作为雷达干扰机共享波形的相位编码序列,所得波形具有优良的固有探测能力和干扰能力。Zhang等[3]对线性调频(Linear frequency modulation,LFM)波形进行噪声频率调制,仿真验证了所设计波形具备高距离分辨率和低旁瓣,同时对LFM脉冲压缩雷达具有更好的干扰效力。杨丹丹等[4]对一般二相编码波形进行噪声相位调制,仿真结果表明所设计波形具备一定探测能力,且尤其对二相编码波形具备更高的干扰效率。韩国玺等[5]提出一种基于混沌遗传的探干一体化波形设计算法,分别以序列自相关旁瓣峰值和信息熵表征波形的探测和干扰性能,实例仿真表明所提算法能够得到较短长度下的序列最优解。Yang等[6]研究了混沌雷达波形设计问题,首先在频域利用混沌序列调制雷达信号群时延,再通过傅里叶反变换将雷达信号变化至时域,所设计混沌雷达信号具备超低副瓣,同时同相和正交分量的幅值均接近高斯噪声。Kulpa等[7]提出一种格子滤波算法用于降低复高斯噪声信号的距离旁瓣和多普勒频移,所得噪声雷达的波形兼顾类噪声性能和目标探测能力。Tang等[8]联合P4码与Costas码设计了一种混合波形编码方法,有效提升了波形的复杂度和探测性能。张亮等[9]提出一种联合相位编码的步进频率低截获(Low probability of intercept,LPI)雷达信号,该波形可得到高于频率步进信号的有效带宽和距离分辨力。Fan等[10]结合P4码和混沌序列频率跳变设计一种射频隐身波形,兼备良好的探测性能和射频隐身性能。Luo等[11]提出一种混沌随机多载波雷达波形,并分析验证其具备良好的LPI性能和反电子对抗能力。Charles等[12]研究频谱型随机调频波形设计问题,利用超高斯族谱作为谱密度模板,有效抑制了波形距离旁瓣,为噪声雷达提供了良好的频率捷变波形。
科学的射频隐身表征参量是进行雷达射频隐身波形设计研究的基础。杨红兵等[13]设计了一种基于噪声调制的对称三角LFM连续波雷达信号,截获因子分析表明该信号射频隐身性能优于常规脉冲多普勒雷达信号。Chen等[14]提出以备测波形与白噪声之间的信息距离作为波形射频隐身性能表征指标,仿真验证该方法能够有效区分常见LPI波形的射频隐身性能。Wang等[15]利用识别理论研究跳频波形参数的设计准则,推导了指定识别概率下截获接收机的最大条件信息熵,用于度量所设计波形的抗分选识别性能。Shi等[16]提出一种最优正交频分复用调制波形的设计策略,保证目标参数估计精度满足需求的同时,最小化系统总辐射功率,辐射功率的合理分配能有效度量波形的射频隐身性能。高超等[17]基于截获接收机原理和LPI波形时频特性构建一种瞬时时宽带宽积射频隐身表征因子,从而能够比较出具有相同截获因子的不同种类波形的射频隐身性能。
为了进一步提升波形复杂度,本文将混沌理论引入探干一体化射频隐身波形设计,提出了两种复合混沌编码方案。另外,现有波形设计方法缺乏对波形干扰性能的定量表征,因此本文将所设计波形与最优压制干扰波形高斯白噪声的信息距离作为干扰性能表征指标,该指标利用基于Wigner谱的KL距离计算所得。最后分别从理论和仿真的角度分析本文所提一体化波形探干性能的折衷关系。
1 探干一体化混沌编码波形设计
混沌的基本特征包含以下两点[18]:
(1)混沌系统的混沌现象是固有的。固有性质体现于系统表现出的复杂性不是在外界干扰下产生的,而是由系统的内随机性决定,即仅由系统自身的因素决定。
(2)混沌系统具有确定性。确定性质体现于混沌系统是一个真实的物理系统,系统当前时刻出现的状态由之前时刻的状态决定,并且所有状态可以完全重现,选择相同的混沌系统参数即可。
Tent混沌序列由以下映射产生

式中:Tent混沌序列初始值x(1)∈[-0.5,0.5];x(n)∈(-0.5,0.5];A为自由参数,趋近于2。Tent离散混沌序列的值在吸引域内服从均匀分布,且序列相关性与自由参数取值和序列长度的关系较为稳定,本文以Tent混沌映射对雷达发射波形进行编码,设计探干一体化波形。
1.1 混沌频率编码一体化波形信号模型
混沌频率编码是指混沌映射系统产生频率编码序列,以此序列对发射波形进行频率调制,即对应一个编码时间段内的信号频率保持不变。基带波形的时域表达式为
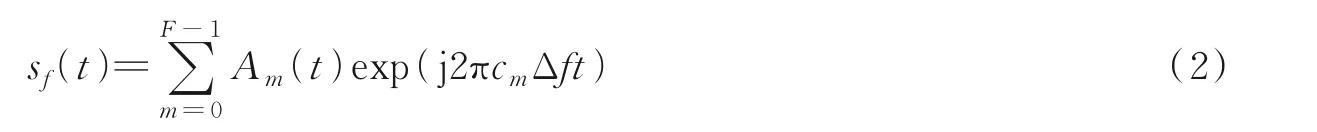
混沌频率编码一体化波形的频谱表达式为

混沌序列由动力学系统x f+1=T(x f)生成,其中T(⋅)为Tent映射函数。为了得到难以预估的混沌序列,假设给定初值x0得到一段长度为L+F的序列,取最后F个映射值作为混沌序列{x1,x2,…,x F}。接着,要对该序列进行处理,已知若频率编码序列出现重复值,使用该序列进行频率编码的波形脉冲压缩结果会在目标位置外出现尖峰,不利于波形进行目标探测。为了避免编码序列量化后出现重复值,对{x1,x2,…,x F}进 行 排 序,最 小 值 的索引值为0,最大值的索引值为F-1,以这样的索引值作为新的频率编码序列。基于混沌编码的一体化波形设计方案如图1所示。

图1 基于混沌序列的一体化波形编码方案Fig.1 Integrated waveform coding scheme based on chaotic sequence
1.2 混沌相位编码一体化波形信号模型
混沌相位编码是指某一混沌映射产生相位编码序列,以此序列对发射波形进行相位调制,即对应一个编码时间段内的信号相位保持不变。基带波形的时域表达式为

混沌相位编码一体化波形的频谱表达式为
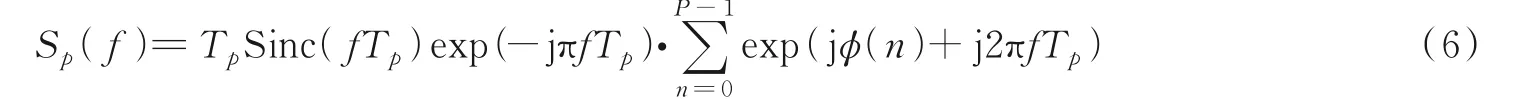
由式(1)得到混沌序列{x1,x2,…,x P},接着进行量化处理,将序列值映射到可选相位集合,由于Tent混沌映射值x p∈(-0.5,0.5],所以相位映射的表达式为

混沌相位编码的一体化波形设计方案类似于图1,其中的排序索引值映射更改为量化处理。
1.3 混沌复合编码的一体化波形信号模型
1.1和1.2节分别给出了频率编码和相位编码方式。本节分别提出两种混沌复合编码波形,分别是脉内频率编码/脉间相位编码波形和脉内相位编码/脉间频率编码波形。
根据式(2)和式(4),脉内频率编码/脉间相位编码的复合编码波形的时域表达式为
式中相位编码码元宽度与频率编码子脉宽的关系为T p=FT f,该类信号带宽等于FΔf。
脉内频率编码/脉间相位编码的复合编码波形的频域表达式为

式中fft(·)表示快速傅里叶变换运算,根据式(3)和式(6)可以得到Sfp(f)。
脉内相位编码/脉间频率编码的复合编码波形的时域表达式为

式中频率编码子脉宽与相位编码码元宽度的关系为T f=PT p,该类信号带宽等于FΔf。
脉内相位编码/脉间频率编码的复合编码波形的频域表达式为
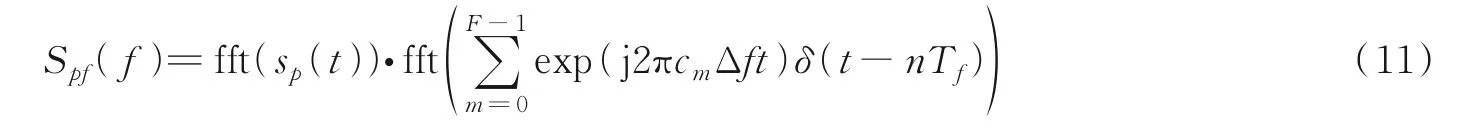
根据式(3)和式(6)可以得到Spf(f)。
2 探干一体化波形性能表征
2.1 探测性能表征
模糊函数是波形设计与分析的有效工具,它能够分析给定波形的分辨率、副瓣、多普勒和距离模糊度等特性,表达式为[19]

式中:s(t)为信号表达式;τ为相对参考目标的时延;ε为多普勒频移。
模糊函数形状由系统设计需求决定。通常,为了得到具备优良探测性能的波形,希望波形具有“图钉状”模糊函数。其主要特征为波形绝大部分能量集中于中心,其他的能量均匀分布于时延多普勒二维平面。模糊函数形状越接近于“图钉状”,波形的距离和速度分辨力越优异。
2.2 干扰性能表征
高斯白噪声被视为最优的压制干扰信号。若探干一体化波形接近于高斯白噪声,则其不仅可以干扰敌方电子设备,还能够降低敌方无源探测设备的截获信噪比,从而提升我方雷达的射频隐身性能。本节将利用随机矩阵与信息距离评估波形与高斯白噪声的相似度。
假设离散高斯白噪声的L个采样值构成集合A={w(1),w(2),…,w(L)},待评估波形的L个采样值构成集合B={s(1),s(2),…,s(L)},其统计特性由波形设计方法决定。通过计算高斯白噪声样本集合A和待评估波形样本集合B之间的信息距离评估探干一体化波形的干扰性能,信息距离越小,波形与高斯白噪声相似度越高,干扰性能越好。信息距离表达式为
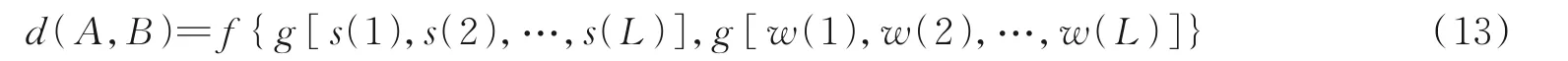
式中:f(⋅)表示距离函数,用于量化集合间的相似度;g(⋅)表示特征函数,用于提取指定集合的特征。
(1)特征函数
设w m(m=1,2,…,M)为l维向量,表示为
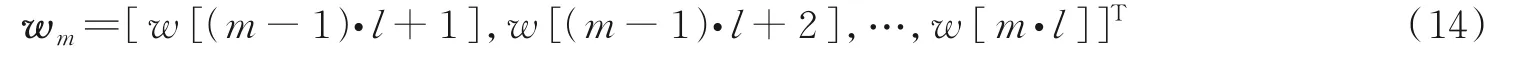
式中:w m为多元高斯概率密度函数的样本,均值为μw,协方差矩阵为R w。若提取待评估波形采样集合B的特征,则s m为未知概率密度函数的样本,概率密度的分布由波形设计方案决定。因为采样值{w(n),n=1,2,…,L}来自独立同分布的随机变量,所以协方差矩阵R w为主对角元素相等的对角矩阵。利用最大似然估计方法得到样本{w(n),n=1,2,…,L}有偏估计的均值和方差为

利用式(15)结果计算得归一化后的样本{wˉ(n),n=1,2,…,L}表达式为得到向量w m归一化后为

当M→∞时,wˉm是均值为0l×l,协方差矩阵为I l高斯概率密度函数的样本,其样本协方差矩阵为



式中:F W l(x)为矩阵W l的一维分布函数,定义为为集合Q的基;λk,k=1,2,…,l为标准化Wigner矩阵W l的特征值。式(19)为一固定函数,可视为高斯白噪声的本质特征,因此,矩阵特征值的概率分布函数可为特征函数,根据式(19)推导W l的渐近谱累积分布函数F(x)为不 完 全Beta函 数

式 中:对 于 任 意 实 数P,Q>0,Beta函 数
(2)距离函数
由上述推导可知,特征函数g(⋅)为概率分布函数,距离函数f(⋅)应能够度量高斯白噪声集合A和待评估信号采样集B产生的概率分布函数间的距离。
敌方截获接收机接收到的信号通常为加噪信号,相较于仅研究探干一体化波形自身的干扰性能,研究其在噪声环境下的干扰性能会更符合实际场景。记特征函数中高斯白噪声集合推导所得标准Wigner矩阵的渐近谱积累分布函数P1(x),待评估波形样本集加噪后构造的Wigner矩阵的渐近谱累计分布式函数为P2(x),P1(x)与P2(x)之间的KL距离为

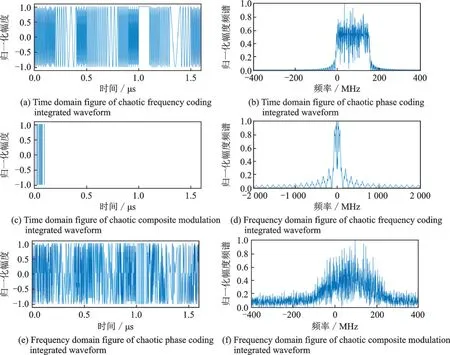
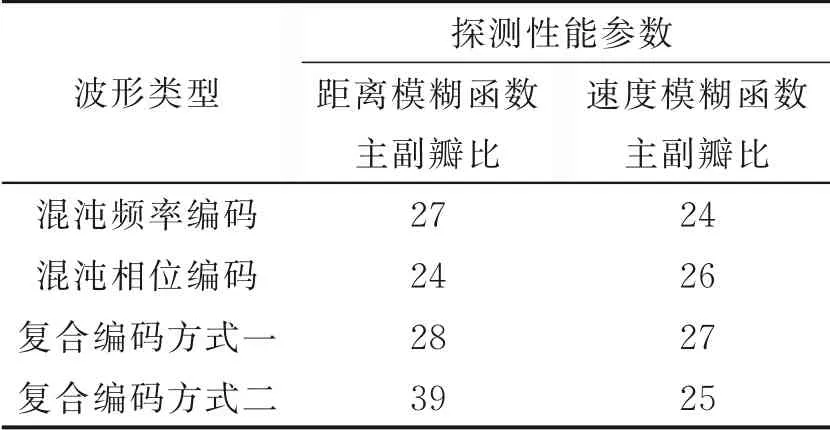
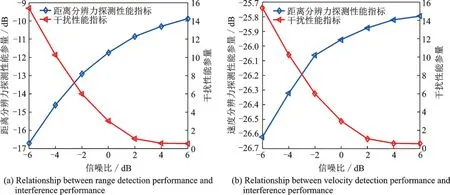
式中p1(x)和p2(x)分别为P1(x)和P2(x)的概率密度函数。为了简化式(21)的计算过程,此处利用概率积分变换,构建一个与{x(n),n=1,2,…,l}等价的数据集{z(n)=F(x(n)),n=1,2,…,l},其中F(x)为随机变量x的真实概率分布函数,从而数据集{z(n),n=1,2,…,l}所源自的随机变量Z服从均匀分布U[0,1],因此式(21)中被减项E(lg(p1(x)))为0。为了采用数值计算方法计算式(21),将区间[0,1]分割为K份,分割点记为uk(k=0,1,2,…,K),且满足0=u0 式中:I(⋅)为指示函数。当K→∞时,∀k>0,有|uk-uk-1|→0,此时KL距离为 当l→∞时,有QZ(u)→u,0≤u≤1,从而因此,待评估波形的KL距离近似为 将脉内频率编码/脉间相位编码的复合编码波形称为复合编码方式一。仿真参数:16位频率编码序列为{12 13 5 2 14 8 6 3 10 15 0 9 7 1 4 11}和16位二相编码序列{0 0ππ0ππ0π0π0πππ0};频率编码子脉宽为0.1μs,即频率跳变单位步长为10 MHz;相位编码码元宽度为1.6μs;采样频率设为5倍带宽。脉内频率编码/脉间相位编码一体化波形的时频域图如图2所示。 图2 脉内频率编码/脉间相位编码一体化波形的时频域图Fig.2 Figures of both time domain and frequency domain of the integrated waveform with intra-pulse frequency cod‑ing/inter-pulse phase coding 将脉内相位编码/脉间频率编码的复合编码波形称为复合编码方式二。仿真参数:16位二相编码序列{0 0ππ0ππ0π0π0πππ0}和16位频率编码序列{12 13 5 2 14 8 6 3 10 15 0 9 7 1 4 11};相位编码码元宽度为0.1μs;频率编码子脉宽为1.6μs,频率跳变单位步长为子脉宽的倒数;采样频率为5倍带宽。脉内相位编码/脉间频率编码一体化波形的时频域图如图3所示。 图3 脉内相位编码/脉间频率编码一体化波形的时频域图Fig.3 Figures of both time domain and frequency domain of the integrated waveform with intra-pulse phase coding/inter-pulse frequency coding 探干一体化波形参数同图2和图3。图4分别给出了4种混沌编码波形的模糊函数图。由模糊图形状可以发现,图4(b)接近于图4(c),而图4(c)中副瓣的波动幅度更小;图4(d)继承了图4(a)距离旁瓣低的优势,并且多普勒域旁瓣得到了显著的抑制。采用复合编码方式的波形模糊函数更接近理想“图钉状”,有利于提升波形的探测性能。 表1对应于图4给出的波形距离和速度模糊函数的主副瓣比。采用复合编码方式一的波形相较于两种单一编码方式的波形在距离和速度分辨力均取得提升;采用复合编码方式二的波形具有更优的距离分辨力。 表1 模糊函数参数Table 1 Ambiguity function parameters dB 图4 一体化波形模糊函数图Fig.4 Ambiguity functions of the integrated waveforms 引入4种射频隐身波形作对比实验,分别为:Tang等[8]提出的改进Costas‑P4波形,张亮等[9]设计的高分辨率PCSF波形,Fan等[10]设计的CCBFM‑P4波形,Luo等[11]设计的改进多载频波形,以及最优压制干扰信号高斯白噪声。 对比波形集为{混沌频率编码波形、混沌相位编码波形、脉内频率编码/脉间相位编码波形、脉内相位编码/脉间频率编码波形、Tang等[8]所设计波形、张亮等[9]所设计波形、Fan等[10]所设计波形、Luo等[11]所设计波形、高斯白噪声}。其中,令KL距离计算中区间 的分割点数等于3;16位频率编码序列为{12 13 5 2 14 8 6 3 10 15 0 9 7 1 4 11},32位二相编码序列为{1 0 1 0 0 1 1 1 0 1 0 1 1 1 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 1}∗π;16位频率编码波形的子脉宽为3.2μs;32位二相编码波形的码元宽度为1.6μs;采用第一种复合编码方案的波形子脉宽设为0.1μs,对应相位码元宽度为1.6μs;采用第二种复合编码方案的波形码元宽度设为0.1μs,对应频率编码子脉宽为3.2μs;对比波形的总脉宽均设置为51.2μs。进行100次蒙特卡罗实验,仿真结果分别如表2和图5所示。 图5 不同信噪比下干扰性能对比图Fig.5 Contrast figure of interference performance at different SNRs 表2 不同信噪比下的干扰性能评价指标值Table 2 Inter ference per formance evaluation index values at different SNRs 当信噪比取值增大时,对于所有波形(除高斯白噪声),基于KL距离的干扰性能指标值增大,即波形类噪声性能变差,截获接收设备能够从中获得更多的信息,验证了该指标的有效性。从指标值排序可以发现,波形干扰性能排序较为稳定,复合调制波形(Tang等、Fan等、Luo等、C1、C2)的干扰性能明显优于单一调制波形(Zhang等、PC、FC),复合调制能够增加波形的复杂度,有利于波形干扰性能的提升。第二种复合编码波形表现出最优的干扰性能,可见脉内相位编码/脉间频率编码方式能够有效提升波形的类噪声性能。高斯白噪声作为最优的压制干扰信号,其干扰性能表征指标均位于最低值,且与信噪比条件无关,经过100次蒙特卡罗实验,其值围绕定值0.027 4波动,验证了干扰性能表征指标的有效性和鲁棒性。另外,当信噪比超过2 d B时,混沌二相编码波形的干扰性能指标趋于稳定,此时环境噪声对波形的影响几乎可忽略,二相编码波形的干扰性能指标随着信噪比的增大最早趋于稳定,体现其固有的良好抗干扰性能。 雷达距离方程能够定量描述雷达系统探测半径、干扰半径及其受干扰程度。当雷达平台发射探干一体化波形进行目标探测、干扰时,不考虑系统损失、地球曲率、大气衰减、无源杂波等影响,其最大探测距离方程为 式中:Rt为最大探测距离;Pt为辐射信号功率;Gt和Gr分别为发射天线和接收天线的增益;λ为探干一体化波形的波长;σ为目标散射截面积;N0为接收机内部的等效热噪声;(S/N)min为最小可检测信噪比。 干扰距离方程为 式中:RJ为干扰距离;G'r(θ)为干扰目标接收天线在接收干扰方向上的增益;PJ为干扰目标接收的干扰信号功率;其余变量含义同式(25)。 进一步描述波形干扰功能,假设探干一体化波形从敌方雷达天线主瓣进入,由式(25)和式(26)推导出敌方雷达的自卫方程为 式中:Rs为敌方雷达受到探干一体化波形干扰时的最大探测距离;P't、G't、λ'、N'0分别为敌方雷达的辐射信号功率、发射天线增益、波长以及接收机内部热噪声;σ'为我方雷达的散射截面积;Pt、Gt、λ分别为我方雷达的辐射信号功率、发射天线增益以及波长;(S/J)min为敌方雷达能够检测到我方雷达的最小信干比。 由式(25)和式(27)可知,增大我方雷达探测距离、减小敌方雷达自卫距离的重要技术途径为提高探干一体化波形的辐射功率。根据3.2节干扰性能仿真结果,随着信噪比的提升,本文所设计波形的干扰性能呈下降趋势,而此时雷达的探测距离、检测概率等探测性能得以提升,因此,通过调整优化雷达辐射功率有利于平衡波形探测性能与干扰性能权衡关系。 针对脉内相位编码/脉间频率编码探干一体化波形,图6展示了一体化波形探测干扰性能的折衷关系示意图。波形距离模糊函数旁瓣积分的倒数设为距离分辨力探测性能参量,波形速度模糊函数旁瓣积分的倒数设为速度分辨力探测性能参量,2.2节KL距离的倒数设为干扰性能参量,所以探测、干扰性能与所选参量呈正比。横坐标信噪比反映了雷达辐射功率,场景一定时,随着雷达辐射功率的提升,探测性能与干扰性能的变化趋势相反,而后趋于平稳,变化趋势与本节理论分析一致。 图6 探测干扰性能折衷关系示意图Fig.6 Figures of tradeoff relationship between detection performance and interference performance 探干一体化波形作为新形式的射频隐身波形对提升作战平台射频隐身性能具有重要意义。混沌序列优良的相关特性、初值敏感性、类噪声性等性质使其适用于探干一体化波形设计。本文基于混沌编码设计了4种探干一体化波形。仿真分析表明:复合编码方式能同时提升波形的探测与干扰性能。同时,混沌序列易于生成且不重复,适用于MIMO雷达波形集设计,在未来的研究中,将着重于将探干一体化波形设计扩展至MIMO体制雷达系统。

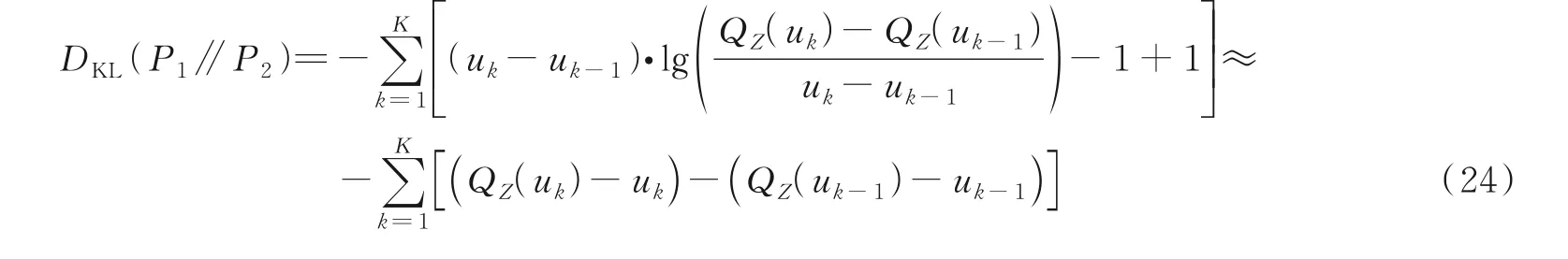
3 仿真与结果分析

3.1 探测性能

3.2 干扰性能


3.3 探干一体化波形性能折衷分析



4 结束语

