考虑环境影响的城市轨道交通电气设备计划维修周期研究*

钱春龙 陈 卓 张 宁

(1. 无锡地铁运营分公司， 214046， 无锡； 2. 东南大学智能运输系统研究中心轨道交通研究所， 210018， 南京；3. 北京城建设计发展集团股份有限公司， 100037， 北京∥第一作者， 工程师)

1 计划维修概述

计划维修是一种基于可变周期的预防性维修策略。城市轨道交通设备在投入使用一段时间后，其故障规律会随某些因素的影响而变化，若采取固定周期的维修策略会增加设备突然停机的次数。因此，设备的维修周期应根据影响因素变化作出相应调整。目前，城市轨道交通设备的维修周期大多参考国有铁路规范及行业内的维修经验制定，而现有设备修程中维修周期多为固定周期，未考虑环境因素对设备运行状况的影响，使得设备维修需求和实际检修“劳动力”不匹配，导致存在不灵活、浪费和不足的现象。尤其是电气设备，其没有机械设备稳定的衰老过程，在不同的季节，电气设备的故障情况有明显不同，因此应制定基于环境变化的可变周期维修计划。

文献[1-6]提出了几种确定设备维修周期的方法，其中以可用度最大及平均维修费用最小为目标建模求解维修周期的方法应用最为广泛，但这些研究在拟合概率分布时均未考虑环境因素对设备运行状况的影响。文献[7-11]引入役龄递减因子和故障率递增因子计算混合式故障率，并将其应用于设备维修周期模型。该模型考虑了受故障次数影响但难以应用于故障较为随机的电气设备。本文通过统计、分析电气设备故障率，确定计划维修周期的可变依据；并结合K-S拟合优度检验方法，建立设备无故障运行时间的条件概率密度模型；再以可靠度为约束条件，制定电气设备的计划维修周期。

2 可变维修周期

分析设备故障数据可知，电气设备在不同季节的故障次数有所不同。以无锡地铁门禁工作站设备为例，图1为2016年6月—2018年4月期间设备的故障统计图。由图1可见，电气设备在夏季(6月—8月)和冬季(12月—2月)的故障次数显著高于其他季节。考虑到数据采集的实际情况，本文选择有历史数据记录的温度作为影响因素参与后续建模过程。

夏季气温较高，高温对设备的电子元器件、绝缘材料及记录介质均有较大的影响。设备温度较高可导致导体表面氧化、可靠性降低、使用时间降低、结构强度降低、数据丢失或故障。冬季气温较低，对设备的高发热器件比较有利，但却对主板、磁盘驱动器等元件有较大的影响。计算机主板在低温条件下运行较为不稳定；磁盘驱动器通常只能在5～55 ℃的环境下工作，温度过低也易造成水汽的凝结和结露现象。

由于部分城市轨道交通电气设备是裸露在外的，环境温度难以控制，其故障情况会随季节的变化而变化。而在室内的设备主要依赖空调设备控制温度，其控制效果亦会在其长时间运行后减弱。因此，本文确定温度为电气设备计划维修周期可变的依据。将温度变量引入电气设备故障分布模型，以制定相应维修周期。

3 基于多项式拟合的计划维修周期条件概率密度模型

制定设备维修周期首先应深入挖掘和分析设备故障数据，明确故障发生的规律。该周期可以通过设备故障概率分布模型表示。由于电气设备系统形式复杂多样，故障原因繁多，设备整体故障规律不显著，维修效果难以定量分析，导致研究对象具有随机、动态、非线性等特征，因此，采用适用于样本总体分布未知的K-S检验方法。该方法在统计电气设备复杂故障分布规律时有明显优势。K-S检验通过无偏拟合设备故障概率分布函数，构建电气设备计划维修故障概率分布模型。结合多项式曲线拟合技术，将温度参数引入该模型，建立电气设备计划维修条件概率分布模型。

3.1 电气设备故障概率分布模型

针对城市轨道交通电气设备，以设备无故障运行时间为研究对象，设设备无故障运行时间为t，故障概率密度函数为λ(t)。根据设备故障概率密度函数常见的3种形式选择合适的分布函数类型，构建电气设备故障概率分布模型。当电气设备故障概率密度函数为常数时，即设备在单位时间内发生故障的概率不变，此时λ(t)=λ，可见设备故障率与时间无关。此时电气设备的故障概率分布函数为指数分布，其故障概率分布模型F(t)为：

F(t)=1-exp(-λt)

(1)

当电气设备故障概率密度函数受多种因素共同影响，且影响因素独立随机时，其相加后即会产生正态分布的效果。在不改变数据性质及其相关关系的情况下，为缩小数据的绝对值，使较为分散的数据集中，同时消除数据的异方差，可取对数变换，此时电气设备故障概率分布函数为对数正态分布。其故障概率分布模型为：

(2)

式中：

φ(·)——标准对数正态分布的故障概率密度函数；

μ——对数均值；

σ——对数标准差。

此外，当电气设备常因某一模块故障引起其整体功能停止运行的情况时，需通过各模块“串联”计算设备整体抵御故障的能力。此时，电气设备的故障分布函数为威布尔分布，其故障概率分布模型为：

(3)

式中：

η——尺度函数；

β——形状参数。

采用极大似然估计方法估计故障概率分布函数的参数。该方法计算简单且估计量与总体参数具有一致性。其基本思想是将处理得到的n个设备无故障运行时间从小到大排序得到数组ti，将其代入故障概率密度函数中取对数求和得到似然函数；再对似然函数求解关于参数的偏导数，对其化简后求解，即可得到上述建立的电气设备故障概率分布模型中参数的估计值。

依据拟合优度检验方法判断样本的分布形式。其基本思想是通过误差平方和最小的判别准则进行分布拟合的假设检验。本文采用K-S检验的方法，该方法在计算时不涉及复杂的随机运算。构造的检验统计量Dn的计算公式如下：

Dn=max{F0(xi)-(i-1)/n,i/n-F0(xi)},

i=1,…,n

(4)

式中：

F0(xi)——上述3种理论概率分布函数。

通过比较Dn与临界值Dn,α(α为给定水平，Dn,α可通过查表[3]获取)的大小，判断构造的电气设备故障概率密度模型的所属类型。

3.2 基于多项式拟合的条件概率密度模型

考虑环境温度影响时，需计算电气设备在一定温度水平下故障的条件概率密度，具体流程如图2所示。

图2中，si为每个子集的温度平均值。根据泰勒定理，任何一个光滑、连续的函数均可展开为1个无穷多项式。多项式拟合的基本思想是：采用多项式表示待拟合的参数变量，采用最小二乘法求解拟合参数ai。

通常多项式的次数越高，误差越小，拟合的精度越高。但多项式次数越高时，待求的参数越多，所需方程也越多；同时还可能会出现过拟合现象，导致模型的泛化性能差，即对温度影响的表述能力差。综合考虑后，采用四次多项式拟合概率密度函数参数。

3.3 电气设备计划维修周期计算

为减少电气设备的停机时间，保证电气设备在大部分时间均可以正常运行，本文选择可靠度为限制条件，利用可靠度函数和故障概率分布函数之间的关系，求解电气设备计划维修周期。可靠度函数R(t)与故障概率分布函数F(t)的关系如下：

R(t)=1-F(t)

(5)

以威布尔分布为例，将其故障概率分布函数代入式(5)，得到其可靠度函数为：

(6)

在可靠度要求不低于目标可靠率R0的情况下，其计划维修周期为：

(7)

不同季节电气设备所处环境的温度水平差异较大，以不同季节每日的平均温度代表该季节的温度水平。电气设备在不同温度水平下的故障概率密度模型中参数不同，因此计划维修周期亦不同。

4 实例分析

以无锡地铁1号、2号线各车站门禁工作站的电气设备为研究对象，对其实行点控。选取2016年6月—2018年7月电气设备的故障记录并进行处理，得到设备的无故障运行时间。应用本文研究方法，为该设备制定维修计划。

采用极大似然估计方法分别构建3种故障概率密度模型(见式(1)—式(3))。其参数估计结果如表1所示。

表1 不同类型电气设备故障分布模型参数估计结果

将样本数据代入式(4)，按从小到大排序，并计算每个观测值对应的累积频率，进而计算Dn。将Dn与Dn,α进行比较，计算结果如表2所示。

表2 不同类型电气设备故障概率分布模型拟合优度检验

由表1可见：

1) 当门禁工作站电气设备故障分布模型的类型为指数分布时，其检验统计量大于临界值。因此，未通过K-S检验，即门禁工作站电气设备故障分布模型类型不可表示为指数分布。

2) 当门禁工作站设备故障分布模型的类型为对数正态分布或威布尔分布时，其检验统计量小于临界值。因此，通过K-S检验，即门禁工作站电气设备故障分布模型类型可表示为对数正态分布或威布尔分布。由于威布尔分布时检验统计量更小，故其拟合优度更好。因此，认为门禁工作站电气设备故障概率分布函数的类型为威布尔分布。

选择样本数据期间，无锡市气温浮动范围为-5～35 ℃。考虑到拟合的数据样本要求，选择5 ℃作为温度水平间隔，应用第3.1节方法检验门禁工作站电气设备在不同温度区间内的故障分布模型类型并进行参数估计。检验及估计结果如表3所示。

以温度区间的平均值为代表，应用图2所述流程，以温度为自变量，分别对温度-尺度参数、温度-形状参数进行多项式拟合，拟合结果为：

(8)

表3 不同温度条件下电气设备故障分布模型检验结果

将拟合结果代入式(3)，即可得到一定温度条件下的设备故障概率分布函数F(t,w)如下：

F(t,w)=1-exp[-(t/(0.001 564w4-0.101 7w3+1.945w2-9.595w+55.74)β]

(9)

其中:

β=4.654 e-0.5x4+0.001 036x3-

0.007 082x2-0.009 742x+0.927 8

(10)

将无锡市冬、夏两个季节的平均气温(夏季平均气温27.67 ℃，冬季平均气温4.07 ℃)以及温度水平中位数15 ℃代入式(9)—式(10)，得到电气设备在各温度下的参数，见表4。

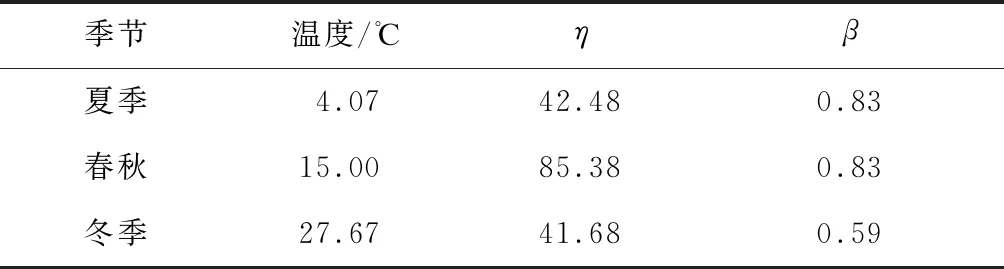
表4 不同温度下设备无故障运行时间分布拟合结果

将计算结果代入式(5)—式(7)，选择目标可靠度为95%，即计算在95%可靠度下1号、2号线门禁工作站电气设备在不同季节的计划维修周期如下：t夏=1.19 d，t春秋=2.38 d，t冬=0.27 d。

根据电气设备检修惯例，对不同季节的计划维修周期取整，制定门禁工作站电气设备的维修计划为：夏季对电气设备实行日检，冬季对电气设备实行半日检，其他季节对电气设备实行双日检。

5 结语

本文通过统计、分析电气设备故障概率，确定温度为计划维修周期的可变依据；通过多项式拟合技术确定温度与概率密度函数中各参数之间的关系。结合K-S拟合优度检验方法，建立一定条件下电气设备无故障运行时间的概率分布模型，再以可靠度为约束条件，制定设备的计划维修周期。将构建的模型和方法应用于无锡地铁门禁工作站电气设备维修计划制定研究中，通过实例分析验证设备故障数据拟合以及计划维修周期计算的可行性。本方法有助于城市轨道交通运营企业制定科学合理的设备维修计划，以节约维修资源，提高设备维修管理水平。