基于自适应布谷鸟搜索的模糊聚类算法

高妍妍 缪祥华，b

（昆明理工大学a. 信息工程与自动化学院；b. 云南省计算机技术应用重点实验室）

聚类是根据数据之间属性的相似度将其划分为不同类簇的过程， 类内相似度尽可能大，类间相似度尽可能小［1］。 模糊C均值（FCM）［2］主要用来解决分类边界过于绝对化的问题，算法简单明了、易于实现。 因为模糊聚类结果的质量很大程度上取决于初始聚类中心的选择，在聚类过程中易陷入局部最优［3］。 因此许多专家学者提出了改进方法。 ZHAO K等利用不动点定理和Banach压缩映射原理，提出了一种适用于使用闵可夫斯基度量作为相似性度量的模糊聚类算法，拓宽了传统模糊聚类算法的应用范围，同时也在算法的全局搜索能力和收敛速度上有了明显提升［4］。 邢海燕等利用粒子群优化算法（PSO）高效的计算能力和全局搜索能力优化了模糊聚类的初始聚类中心和权值， 并建立了高正确率的分类模型［5］。DEY S等利用量子粒子群算法生成数据的模糊聚类中心，并用此聚类多维数据［6］。王龙等在自适应烟花算法优化中引入了多维相似性距离改进模糊C均值算法， 改进后的算法在彩色图像分割方面取得了良好的效果［7］。 肖满生等兼顾区间中值和区间大小并利用控制区间大小的因子改进了模糊聚类算法，优化了模糊聚类算法在区间不确定性数据上的划分系数和正确等级［8］。 吕冰垚等将粒子群算法与遗传算法结合进行全局搜索优化模糊聚类算法的聚类中心，提高了图像的分割精度［9］。SUBRAMANIAM M等在进行语义分析时，根据相似性在改进的萤火虫算法的帮助下找到最优特征，并将此用于模糊聚类，提高了语义分析系统的准确性［10］。 KUMAR A等在工蜂群算法的帮助下使模糊聚类算法跳出了局部最优，利用UCI常见的数据集对改进后算法的性能进行了验证［11］。 高云龙等利用K最近邻的方式来估计样本是噪声的可能性，自适应调整参数，降低噪声对模糊聚类的影响，提高了模糊聚类算法的兰德指数和鲁棒性［12］。 汤正华利用改进的蝙蝠算法自动确定簇中心和簇数目， 将蝙蝠位置作为簇中心，利用Levy飞行摆脱局部最优［13］。 董发志等针对模糊聚类算法的缺陷，将遗传算法优化用于优化初始聚类中心，从而达到优化聚类的目的［14］。 PANTULA P D等为提高聚类效率，将人工神经网络引入模糊聚类之中， 提出了神经模糊C均值聚类算法［15］。 ZHANG Z X和GU B P将模糊聚类和PSO算法相结合，将其用在入侵检测领域，提高了检测的效率和准确度［16］。 上述算法，尤其是各类型群智能算法的使用提高了聚类结果的准确率，但群智能算法最终结果的好坏依赖于参数与阈值设定的合理性，增加了结果的不确定性。

布谷鸟搜索算法相较于其他发展成熟的算法，更易于理解、使用到的参数更少、全局寻优能力也有所提高， 并且可以和多种算法相结合，适用程度更广泛。 然而，在传统的布谷鸟算法中步长控制因子与发现概率是固定不变的，因此算法容易出现早熟、最优解精度低、甚至找不到全局最优值以及收敛速度慢等弊端。 基于以上分析，笔者令步长控制因子和发现概率随着搜索阶段自适应变化来进一步提升布谷鸟算法的搜索性能，并将其用于搜索模糊聚类算法中最优的初始聚类中心，从而进一步提高模糊聚类的准确率。

1 布谷鸟搜索算法的自适应

1.1 布谷鸟搜索算法

CS算法通过随机行走的Levy飞行进行高效搜索，但在不同的搜索阶段，步长控制因子α和发现概率Pa一成不变， 对全局搜索和局部搜索的精度产生了极大的影响。 如果搜索步长相对较小，则算法偏向于局部的精细搜索， 全局搜索能力差；如果搜索步长偏大，则算法全局搜索能力增强，局部搜索能力降低，容易略过全局最优解。 同样，如果发现概率Pa过小，则容易陷入局部最优，收敛到当前的坏结果， 反之Pa过大时则很难收敛于全局最优解。 因此两者的设置对算法的收敛速度会产生较大影响。

1.2 步长控制因子和发现概率自适应的CS算法

自适应布谷鸟 （Adaptive Cuckoo Search，ACS）算法通过判断当前的搜索阶段，动态设置α和Pa，使其可以自适应当前的搜索环境。在算法前期， 应该注重全局搜索能力，α应该取较大的值；在算法后期， 已经收敛到全局最优解的附近，因此α应该取较小的值，注重局部的精细搜索，提高解的精度。 将式（1）中的固定的α值更新为：

其中，T为总迭代次数，ti为当前迭代次数。

则改进后的更新解位置的式（1）可更新为：

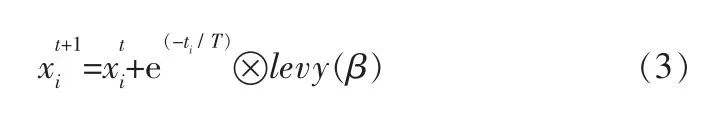
当新解产生后，发现概率Pa与在［0，1］区间内产生的随机数r进行比较， 如果r＜Pa则保留当前解，反之则按偏好随机行走方式生成新解：

随着迭代的进行， 解的质量也在不断提高，在传统CS算法中发现概率Pa大多取值为0.25，固定的发现概率在应对不同迭代周期、不同优质程度的解时应变能力不足，无法做出均衡调节。 自适应发现概率定义如下：

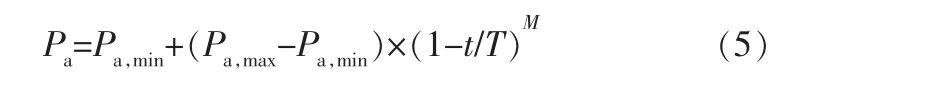
其中，Pa，max和Pa，min分别 表示Pa的最大 值和最小值；M是非线性因子， 当M=1时，Pa是线性变化的， 到迭代后期Pa会长时间保持较小值影响搜索效率，因此Pa采用非线性方式减小。根据大量的仿真实验证实Pa，max=0.75，Pa，min=0.1，M=0.5时效果最好。 在迭代过程中Pa随着解的质量不断提高逐渐减小，与自适应步长相适应。 在早期迭代中，较高的发现概率会促进解多样性的增加，在迭代后期减小对新解的发现概率， 可以更好地保留最优解，增强算法的寻优能力。 Pa和α随迭代次数变化曲线如图1所示。

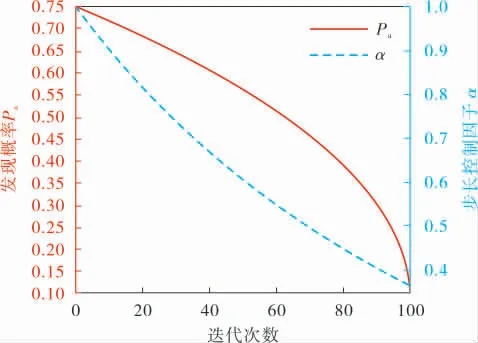
图1 α和Pa随迭代次数变化曲线

从图1可以看出，α和Pa的值与迭代次数呈负相关。 在迭代前期，α下降快，Pa保持较大值，可以快速进行全局搜索，提高全局寻优的性能；在迭代后期，算法已经收敛于全局最优解的周围，α和Pa都保持较小值进行更为精细的搜索， 从而提高解的精度。

1.3 实验与分析

为验证ACS算法 的性能，选f1（Eggholder）、f2（Rastrigin）、f3（Schwefel）、f4（Michalewicz） 和f5（Sphere）（表1）5个标准测试函数进行实验，其中测试函数f1～f3中，由于存在许多局部最小值，因此算法寻找全局最优解的难度要高于另外两个函数。

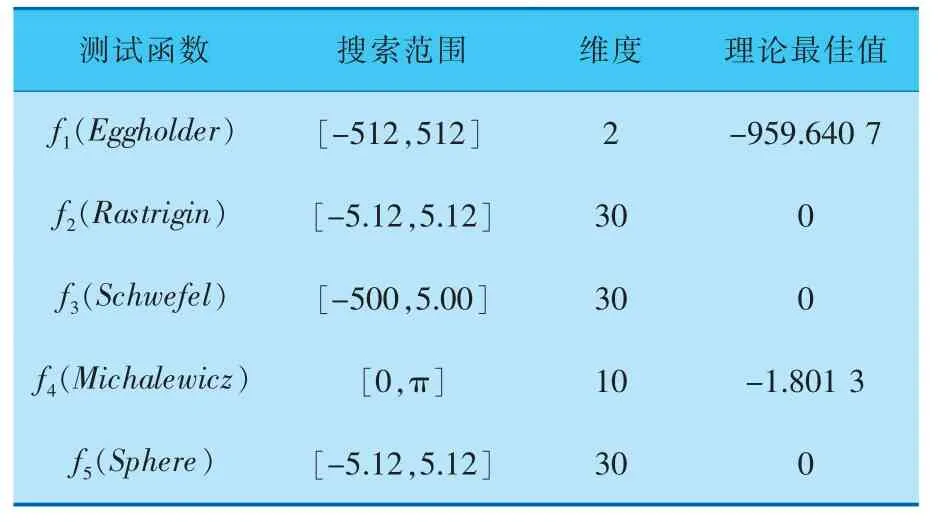
表1 标准测试函数

为验证ACS算法的性能， 将其与CS算法在Python3.7环境下进行对比实验。 实验参数如下：寄生鸟巢个数为20，最大迭代次数为50，步长控制因子α和发现概率Pa分别按式（2）和式（5）动态调整，更新解的位置按式（3）进行调整。 为了降低偶然性对实验结果的影响，基于相同条件将两个算法独立，取运行50次的结果作为评定算法性能的依据。 通过平均值和最优值可以看出解质量的好坏，通过标准差可以看出算法是否稳定。 具体实验结果见表2，收敛曲线如图2所示。

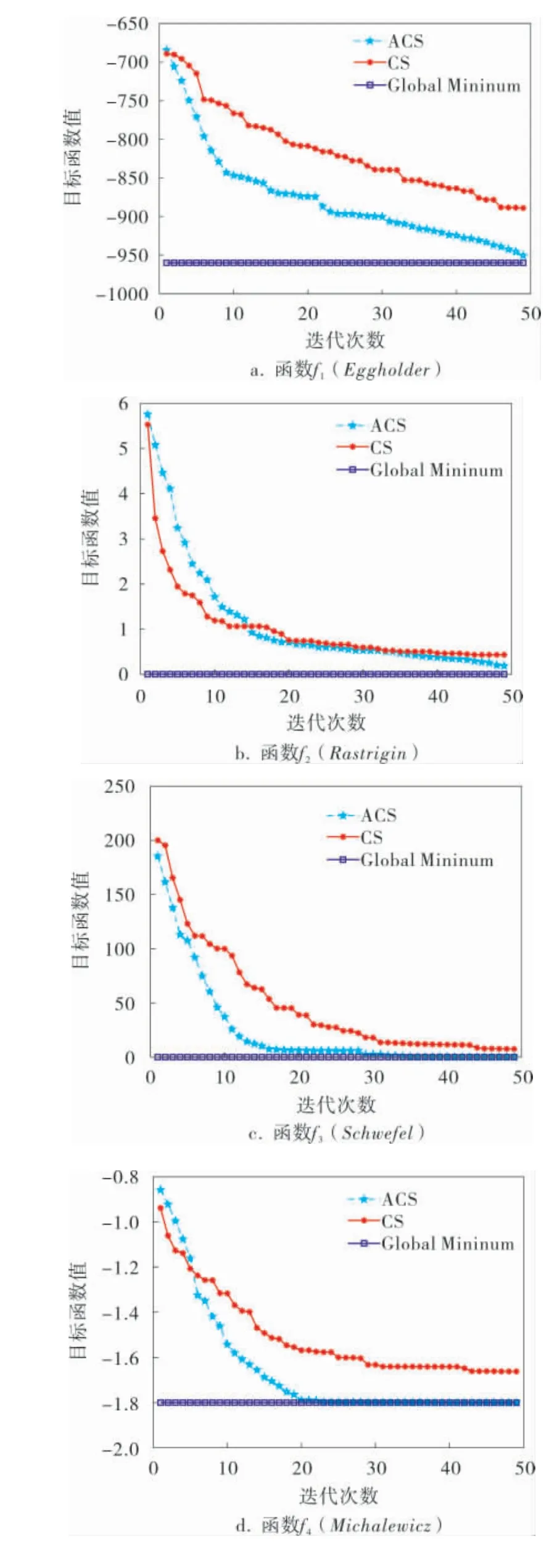
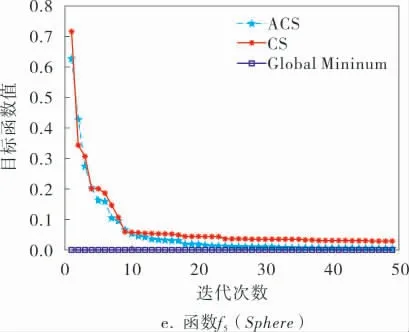
图2 5种测试函数的收敛曲线

表2 两种算法在标准测试函数上的优化结果

由表2可知，ACS算法无论在高维、低维，还是在多模态函数方面的求解精度都优于CS算法。 在搜索范围较大的函数f1、f3上求解的质量有了有效的改善，在搜索范围较小的函数f2、f4、f5上，可以观察到ACS算法解的精度相较于CS算法有进一步的提升。 通过对比表2中ACS与CS算法的标准差，可证实前者计算的稳定性要高于后者的。 将图2a～e进行对比可以看出，ACS算法可以在较短的迭代周期内迅速搜索到全局最优值，且收敛速度高于CS算法。 对于搜索范围大的函数f1、f3， f1中两个算法都以较好的收敛速度靠近最优解，相对于CS算来说，ACS算法的寻优效率更高；在函数f3中，虽然在迭代前期CS算法解的质量要优于ACS算法，在迭代中期时两个算法同时陷入局部最优，但在算法迭代后期，ACS算法凭借自身的优势摆脱局部最优陷阱，继续向全局最优解靠拢。 对于搜索范围较小的函数f2、f4、f5，ACS算法和CS算法均在50次迭代内找到了高质量的解， 但是ACS算法在收敛速度和解的精确度方面都优于CS算法。

2 基于ACS的模糊聚类算法

FCM算法是按隶属度将样本划分为C个聚类的过程，其目标函数为：

其中，U为模糊隶属度矩阵；uij为j类中第i个样本的隶属度；dij是从第i个数据样本到第j个聚类中心的欧几里得距离；P为聚类中心矩阵；m为模糊指数，通常取m=2。

FCM算法的初始聚类中心产生方式具有高度随机性，如果聚类中心的质量越高则聚类的效果越好， 相反较差的聚类中心则会得到质量不好的聚类结果， 从而使得算法在计算过程中产生一定的波动性。 因此，利用ACS优越的搜索能力寻找到质量最佳的初始聚类中心， 然后再进行后续的聚类过程，从而改善FCM算法对初始聚类中心敏感性这一缺点，并帮助模糊聚类跳出局部最优解。 笔者结合ACS算法和FCM算法的优点提出了基于自适应布谷鸟搜索的模糊聚类算法（Adaptive Cuckoo Search Based Fuzzy C-Means，ACSFCM）。

2.1 编码与目标函数

如果待聚类样本拥有d维特征，将被划分为k类，则布谷鸟算法的解由k×d矩阵构成。 其编码结构如下：

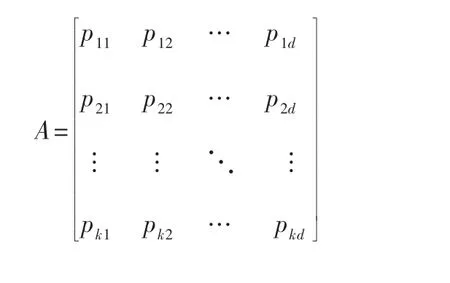
其中，p11，p12， …，p1d表示第1个类的聚类中心；pk1，pk2，…，pkd表示第k个类的聚类中心。

采用式（6）目标函数J（U，P）来衡量解的优越性。 目标函数J（U，P）的值越小，表明其解的质量越高，聚类效果越好。

2.2 算法流程

在保持FCM算法思想的基础上， 结合ACS算法，新算法ACSFCM的实现步骤如下：

a. 初始化种群， 将数据集D中的各个数据作为一个可行解，生成一组随机解A1，A2，…，An，定义目标函数；

b. 计算各个解的目标函数值，得到当前的最优解Abest；

d. 计算新解的目标函数值，并与更新前的Abest比较，如果新解的质量更高则更新Abest；

e. 以发现概率Pa随机淘汰部分解， 按式（4）的方式获得一组新解；

f. 执行上述过程， 判断是否达到结束算法的迭代次数要求，没有达到则执行步骤c，达到则输出全局最优解Abest；

g. 执行在指定聚类中心情况下的模糊聚类算法。

3 ACSFCM算法的实验与分析

为了验证ACSFCM算法的性能， 将其与FCM算法、PSOFCM算法［16］和利用CS算法改进FCM的CSFCM算法在UCI常用的4个数据集（表3）上进行反复实验，实验结果详见表4。 各算法在数据集上的聚类准确率对比如图3～6所示。 实验参数设置如下：模糊指数m=2，种群规模n=15，迭代次数为20次，Levy飞行参数为1.5，Levy飞行的步长控制因子和发现概率Pa使用ACSFCM算法采用自适应参数，CSFCM算法则选择固定的α=0.7、Pa=0.25。文献［16］的PSOFCM算法使用改进的PSO算法来优化FCM算法的初始聚类中心，主要参数设置如下： 模糊指数m与种群规模n与ACSFCM算法相同，自我学习因子c1和全局学习因子c2为0.5，惯性系数w0为0.8。

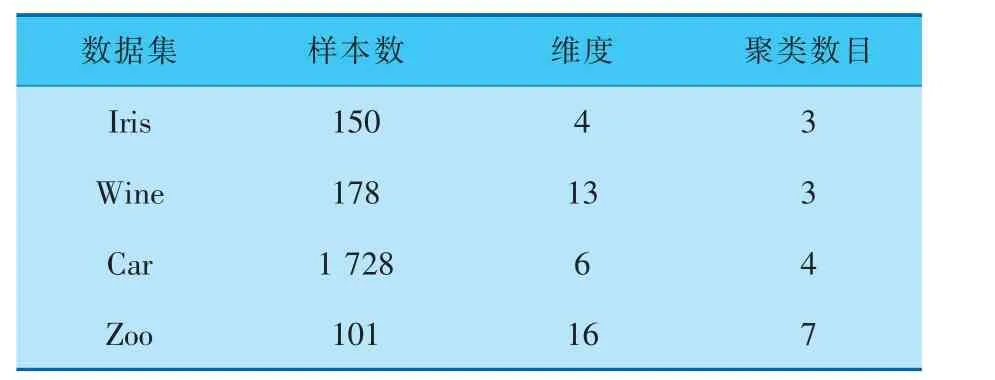
表3 数据集详细信息

比较分析表4中的数值可以得出，4种算法中ACSFCM算法的目标函数值和聚类准确率均优于其他3种算法。 在Iris数据集上（图3），ACSFCM的目标函数值要小于其他3种算法，聚类准确率也达到了91.6%，相较于FCM算法81.3%的准确率提升了10.3%， 虽然ACSFCM 的准确率要高于PSOFCM算法， 但其稳定性要低于PSOFCM算法；在Wine 数 据 集 上 （图4），ACSFCM 的 准 确 率 为88.8%， 比CSFCM算法的准确率提高了12.9%，证明了ACS算法在优化模糊聚类中心提高聚类效果上有作用，其他3种算法的波动较大；在Car数据集上（图5），ACSFCM的准确率相较于FCM算法提升了4.2%，与其他数据集的准确率相比提升并不明显，但从准确率对比图中可以看出稳定性得到了提高；在Zoo数据集上（图6），ACSFCM的准确率相比于FCM、PSOFCM、CSFCM 分别提升了10.2%、4.2%、3.1%， 而在整体稳定性上的表现与其他数据集相比波动较大。 总结图3～6可知，ACSFCM算法在较高聚类准确率的前提下，在整体的稳定性上也具有明显优势； 与PSOFCM 算法相比，ACSFCM需要人为设定的参数和阈值较少， 并且对参数设置的依赖性更低。简而言之，ACSFCM有着较其他算法更佳的聚类准确率和稳定性。

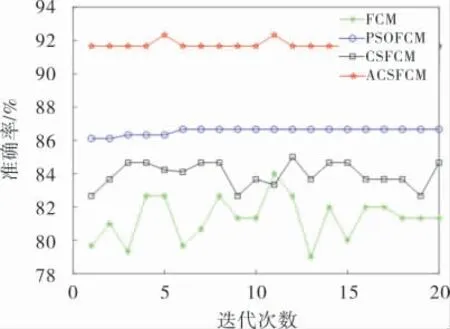
图3 Iris数据集聚类准确率对比

图4 Wine数据集聚类准确率对比

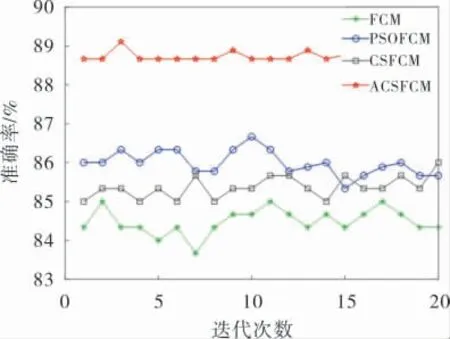
图5 Car数据集聚类准确率对比

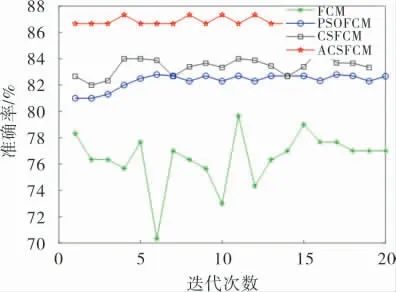
图6 Zoo数据集聚类准确率对比

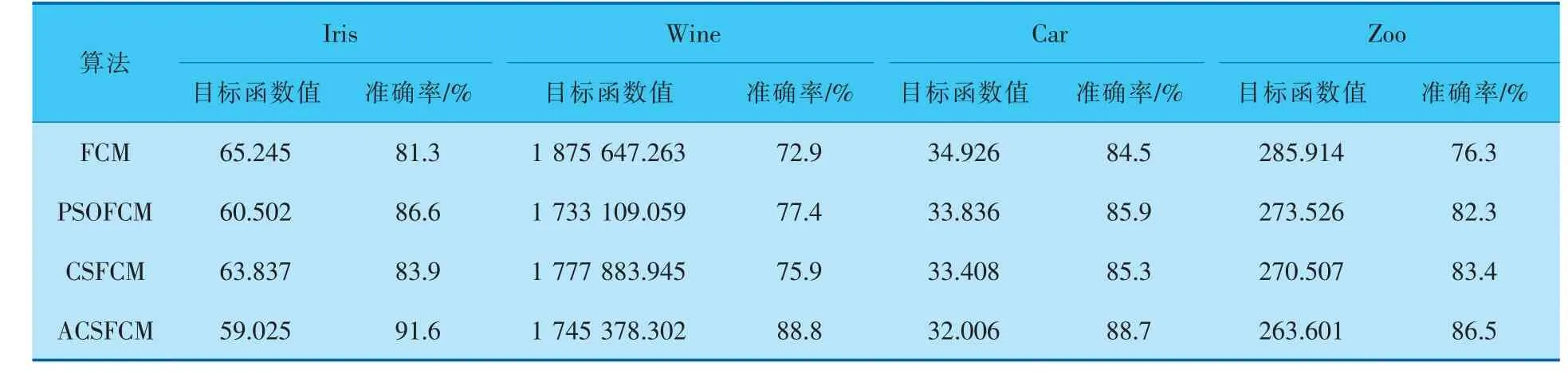
表4 4种数据集的聚类结果

4 结束语

由于FCM算法对初始聚类中心选取敏感性的缺陷， 笔者基于ACS算法高效的搜索能力提出了ACSFCM算法。 算法在搜索的过程中根据搜索阶段自适应调节步长控制因子和发现概率的参数设置， 提高算法的收敛速度和寻优精度。ACSFCM通过找到最佳的初始聚类中心， 来提升模糊聚类算法的聚类准确率。 实验结果证明：ACSFCM算法相较于PSOFCM、FCM、CSFCM算法，在聚类的准确率和稳定性方面有了显著提升。ACSFCM算法在一些细节上还有强化的空间，如ACS算法在Levy飞行的过程中方向是盲目的，影响算法的寻优效率， 未来的研究可以对ACS算法的搜索方向加以控制，使算法可以更快、更准确地向最优解靠近，并将其应用到更广泛的领域。