计及季节性氢储的新能源汽车供能站分布式规划模型
翁菖宏,胡志坚,张承圣,李想,王放
(1.国网福建省电力有限公司福州供电公司,福州市 350009;2.武汉大学电气与自动化学院,武汉市 430072;3.国网福建省电力有限公司经济技术研究院,福州市 350012)
0 引 言
近年来,为实现能源的可持续发展,国际社会将大力发展新能源汽车(renewable vehicle,RV)作为交通领域低碳化的重要措施。在各国政策和发展战略的引导下,新能源汽车已形成了以电动汽车(electric vehicle,EV)为主,燃料电池等其他新能源汽车为辅的发展模式。然而,新能源汽车产生的大规模充电需求与燃料制备对应的电能需求给传统电网安全稳定运行带来了巨大挑战[1-2]。因此,开展电-氢联合供应的新能源汽车供能站规划方法研究是重要课题之一。
目前,一些前沿研究已经围绕含新能源汽车接入的供能站规划方法展开。文献[3]提出了一种考虑新能源不确定性和系统可靠性的概率优化模型对含电动汽车和氢燃料电池汽车(hydrogen fuel cell vehicle,HFCV)接入的微网进行规划。然而,该研究未考虑交通网实际情况对用户用能时空分布的影响,规划模型的精度较低。文献[4]利用Wardrop均衡理论表示电动汽车与燃油车的混合稳态均衡,有效表征了充电负荷的空间分布情况,并基于此提出含快充桩的综合能源站规划模型。但上述文献均以全信息拥有者的角色对系统进行全局规划。事实上,能源部门与交通部门分属于2个完全独立的系统,在实际工作中能源商很难获取交通系统的敏感数据。分布式求解是解决全局规划中信息局限性的有效方案。文献[5]提出丹齐格-沃尔夫分解与列生成结合的方法实现了大量微网的隔离优化。文献[6]将配电网-天然气网联合规划问题转化为包含2个网络和若干个耦合站点的新架构,并利用交替方向乘子法(alternating direction multiplier method,ADMM)直接进行迭代求解,但这忽略了ADMM对于非线性问题收敛性差的缺陷。并且,现有研究中鲜有分布式算法在含电-交网络的供能站规划问题上的个性化应用。
此外,储能装置由于其削峰填谷的优秀特性在新型电力系统研究中经常涉及。文献[7]探讨了电储能和气储能在大规模新能源汽车接入背景下的作用,验证了联合储能策略可以平抑充电负荷并提高系统经济性。氢储能作为新兴的储能形式之一,有着清洁、高效、经济的显著特点。随着装置制造技术不断提升,氢储能逐渐成为供能系统的主流设备之一。文献[8]提出了一种含氢储水装置的综合能源系统架构,其平衡了多种能源,提升了新能源利用效率。文献[9]表明利用低温存储等方式可以实现氢能的长时间大规模经济储存,由于该特性,季节性氢储能成为新的氢储策略。但是,目前仅有少量研究涉及该策略。文献[10]提出了一个含电-氢-天然气多能源形式的综合能源站的规划模型,仿真结果表明季节性氢储可以有效解决可再生能源输出的不确定性,但其侧重于研究氢储与汽轮机等综合能源设备间的相互影响。文献[11]提出了一种包含季节性氢储的电-氢-热-冷联供的全生命周期规划模型,验证了季节性氢储在岛式综合能源站布局的经济性。综上,仅有少量文献涉及季节性氢储在新能源汽车供能站规划中的应用,并且未见文献系统性探讨普通氢储能、季节性氢储能、电储能间的关系。
为填补上述研究空白,本文首先提出一个包含配电网、电-氢联合供能站、交通网的新能源汽车供能系统(renewable vehicle energy supply system,RVESS)规划框架。在RVESS中,运用冬-夏转移的季节性氢储策略并用混合整数线性表达进行跨场景建模;其次,为隔离交通网架信息、全区域出行需求等核心隐私信息,针对电-氢联合供能站规划问题,个性化地定制一种包含松弛、近似、收缩三阶段的分布式迭代求解方案;最后,基于IEEE-33节点配电网和12节点典型交通网联合系统进行仿真验证,并针对电储、氢储、季节性氢储的配合关系进行系统性分析。
1 新能源汽车供能系统架构
电-氢联合供应的新能源汽车供能系统架构如图1所示。基于该架构,电能被直接利用或转化为氢能以满足EV和HFCV的日常用能需求。RVESS主要由三部分组成:
1)联合供能站(combined energy supply station,CESS):风力发电机组(wind generation,WG)、电解槽(electrolytic cell,EC)、快速充电桩(fast charging facility,FCF)、氢加注机(hydrogen injector,HI)、电储(electric storage,ES)、氢储(hydrogen storage,HS)、季节性氢储(seasonal hydrogen storage,SHS);
2)配电网:吸收/提供CESS剩余/缺额电量;
3)交通网:由主要节点和主干道构成,网络内考虑EV、HFCV和燃油车等常规汽车(normal vehicle,NV)的分布情况。

图1 新能源汽车供能系统架构Fig.1 Architecture of a RVESS
在该架构下,新能源汽车的电/氢用能需求通过CESS耦合至电网中,对应的空间用能分布将影响供能系统的规划方案;同时,不同规划方案下的各CESS供能能力将影响交通用户的出行补能方案,供能系统和交通系统相互影响,实现二者的深度融合。
2 RVESS数学模型
2.1 联合供能站模型
1)季节性氢储。
氢的密度低、性能好,氢储被视为具有广泛运用价值的新兴储能形态。此外,风机出力呈现季节不均匀的特点,即冬季出力高、弃风现象严重,夏季出力低、供电能力差。为了平衡该自然因素导致的不良现象,本文利用具有良好储存特性的液态季节性氢储实现电能的空间尺度转移,其运行机制如图2所示,将冬季剩余电量通过转化为氢能储存在SHS中用于夏季时为燃料电池汽车提供氢能以减小夏季HFCV接入增大电网供能的压力。
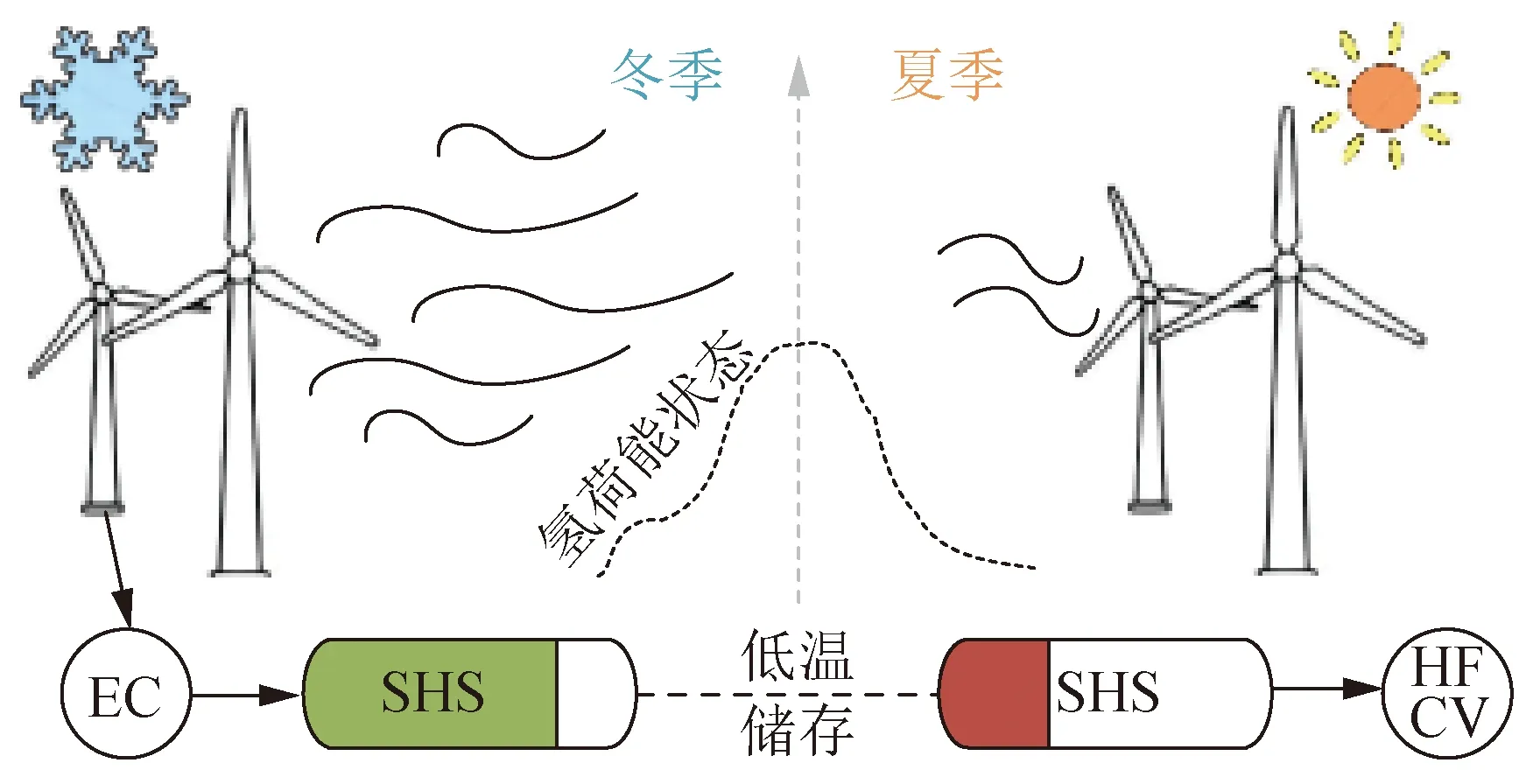
图2 冬-夏转移的季节性氢储运行机制示意Fig.2 Schematic diagram of SHS operating mechanism for winter-summer transfer
相关表达式如下:
(1)
(2)
(3)
(4)
(5)
(6)


2)普通氢储和电储。
ψω,k=ψω-1,k+ηλω,k
(7)
(8)
(9)
(10)

普通氢储能和电储能的充放能特性由式(7)—(10)统一表达,分别为荷电状态约束、充放速率约束、储存容量约束、可循环约束。其中,λ为储能动作量的集中表达。
3)风电。
(11)
(12)
(13)

式(11)和式(12)分别限制了风电出力的有功和无功范围;式(13)为安装容量约束。
4)电解槽。
(14)
(15)
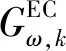
式(14)为电解槽的用电量和产氢量的关系;式(15)为设备的最大产量限制。
5)快充桩和氢加注机。
(16)
(17)
(18)
(19)
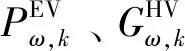
式(16)和(18)表示车流量与用能需求的关系式;式(17)和式(19)约束了设备供能能力。
6)物质流平衡约束(电-氢-交通耦合约束)。
(20)
(21)
(22)
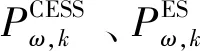
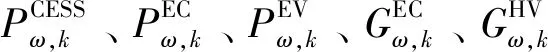
7)设备建设数量约束。

(23)
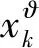
2.2 交通网侧模型
本文采用考虑基础交通流的用户均衡模型[12]对新能源汽车的空间用能分布进行模拟。该模型基于Wardrop用户均衡理论[13],在已知的NV历史分布下,模拟RV用户的理性出行行为。均衡模型表达式为:
(24)

(25)
(26)
(27)
(28)
(29)

式(24)约束了用户仅选择当前最优方案出行;式(25)表明出行成本包含道路通行时间和CESS附加等效时间,前者用美国联邦公路局函数描述,如式(26)所示,后者从系统宏观层面进行讨论,具体的可通过交通管制、调整充电费用等方案实现,式(27)约束了其变化范围;式(28)表明道路由RV车流和NV车流相叠加;式(29)为出行需求约束。
2.3 配电网侧模型
(30)
(31)
(32)
(33)
(34)
(35)
(36)
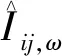
式(30)、(31)约束了配网中的有功和无功平衡;式(32)表示节点间的电压关系;式(33)—(36)分别约束了视在功率、线路功率、节点电压、上级供电能力。
3 RVESS的规划模型及其求解方案
本节站在具有RV供能设备投资业务的能源商角度,以全系统的投资-运行费用为优化目标提出RVESS的规划模型。为应对供能系统和交通系统间存在的隐私信息屏障,原规划模型被分为能源部分(energy part,EP)和交通部分(transportation part,TP)2个子问题并尝试利用标准ADMM进行求解。然而,标准ADMM无法保证分解问题具有很好的收敛性[14-15],特别是求解含交通网的大型联合规划问题。所以,本文基于分块固定求解的核心思想并结合ADMM提出含松弛-近似-收缩三阶段的个性化求解方案。
3.1 集中式模型
1)目标函数。
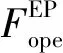
(37)
(38)
(39)
(40)
(41)
(42)
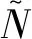
式(42)为交通网的拥堵等效费用,表明了规划者对社会效益的关注。
2)约束条件。
模型约束条件包含配电网约束、供能站约束和交通网约束,如式(1)—(36)所示。其中,式(24)、式(26)、式(33)为非线性约束,参照文献[16]利用大M法、分段线性化方法、二阶锥松弛技术处理,本文不再赘述。
3.2 分解模型
本文以原模型中各CESS截获的RV交通流量f′作为EP和TP的共识变量,并引入fEP和fTP分别表示EP和TP的RV空间流量分布。将相关约束式(16)、(18)、(24)、(28)、(29)改写为式(43)—(47)并添加耦合约束式(48),如下:
(43)
(44)
(45)
(46)
(47)
(48)
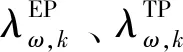
(49)
(50)
由此,原问题P-RVESS被分解为混合整数二阶锥问题SP-EP和混合整数线性问题SP-TP,2个子问题归纳如下:
子问题SP-EP为:
(51)
子问题SP-TP为:
(52)
3.3 定制ADMM求解方案
为保证分布式算法的收敛性,本文针对电-交耦合模型提出了一种基于ADMM的分布式求解方法。定制ADMM可分为松弛、近似、收缩3个过程。
1)松弛:将分解问题中的整数变量松弛为有界连续变量,利用标准ADMM求解松弛问题的最优解;
2)近似:利用分块确定整数变量的原则,获取满足分解问题可行解;
3)收缩:通过对连续变量和整数变量的迭代优化,获取高质量的问题近似解。算法流程如图3所示,其中,“*”表示步骤与SP-EP相关;“#”表示该步骤与SP-TP相关。上标′表示该问题目标函数中不含拉格朗日附加项。
具体步骤如下:
步骤1:将SP-EP和SP-TP中的所有离散变量松弛为有界连续变量,主要包括设备投资数量变量、出行方案选择布尔变量和辅助变量,调用标准ADMM求解松弛问题,得到松弛问题的全局最优解。
步骤2:求解SP-EP′,获取当前RV空间分布下的EP整数可行解。
步骤3:依据步骤2的结果固定EP的整数变量并保持交通网布尔选择变量松弛,调用标准ADMM求解当前松弛模型的最优解。
步骤4:校验SP-TP′是否有可行整数变量满足步骤3获得的RV空间流量分布,若有,则直接进入收缩环节;若无可行解,执行步骤5。
步骤5:求解邻域可行性问题P-near以获取最接近的可行流量分配方案。由于RV的用能高峰和低谷给供能系统带来的影响是最恶劣的[17],为了获得较高质量的可行整数解,P-near目标函数由所有场景偏差量和极端场景偏差惩罚量构成,如式(53)所示。约束条件不仅包括原TP相关约束,还新增式(54)、(55)关系约束。

图3 定制ADMM算法流程Fig.3 Flow chart of tailored ADMM algorithm

(53)
(54)
(55)
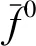
步骤6:求解SP-EP′,得到步骤5用能分布下的最优能源规划方案。至此,获得一组较优且原问题P-RVESS可行的混合整数解。
步骤7:固定P-RVESS全部离散变量,利用标准ADMM方法求解最优连续变量解。
步骤8:固定共识变量f′,分别求解SP-EP′和SP-TP′,获取2个子问题的混合整数解。
步骤9:校验迭代收敛情况。当连续2次迭代求解得到的离散变量不发生变化且耦合变量不变则表示模型收敛,求解结束;否则,继续迭代,返回步骤7。
4 算例分析
本文基于IEEE-33节点配电网和典型12节点交通网组成的电-交联合系统对所提模型与方法进行仿真分析。联合系统中包含3座CESS,其中1、2、3号CESS分别位于配网近端、中端和远端,具体的备选站址及其耦合关系如图4所示。备选储能设备和其他设备参数信息分别如附录表A1和A2所示,规划模型涉及的重要参数如附录表A3所示,相关数据参照文献[1,16]并在一定范围内调整。
4.1 季节性氢储建设先进性分析
为了直观反映在CESS中建设季节性氢储的先进性,设置本文模型(算例A)和不考虑SHS建设(算例B)2种对照情形,设备建设情况如表1所示,系统经济情况如表2示。
结合表1和表2对照分析算例A和算例B规划结果可知,算例B相较于算例A多建设2台WG,风机投资增加了13.3%,而全年实际新能源送出量只同比增加8.13%。并且,未引入SHS将导致大规模的弃风,算例B的弃风惩罚费用高达654.68万美元,较算例A增长了6.55倍。系统总费用则由算例A的1 108.97万美元增长至算例B的1 538.78万美元,涨幅高达38.76%。
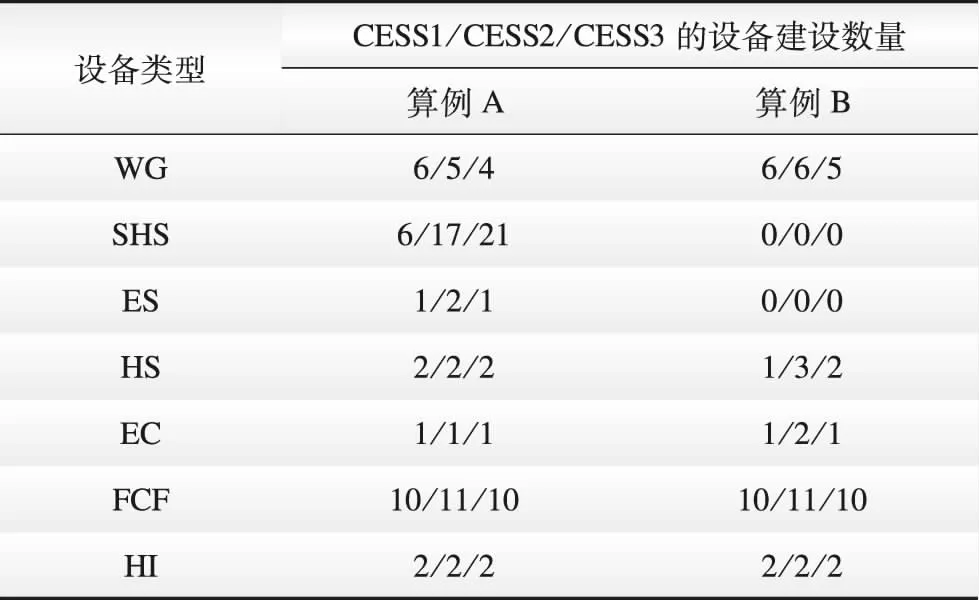
表1 算例A和算例B的设备建设情况Table 1 Equipment construction in case A and B
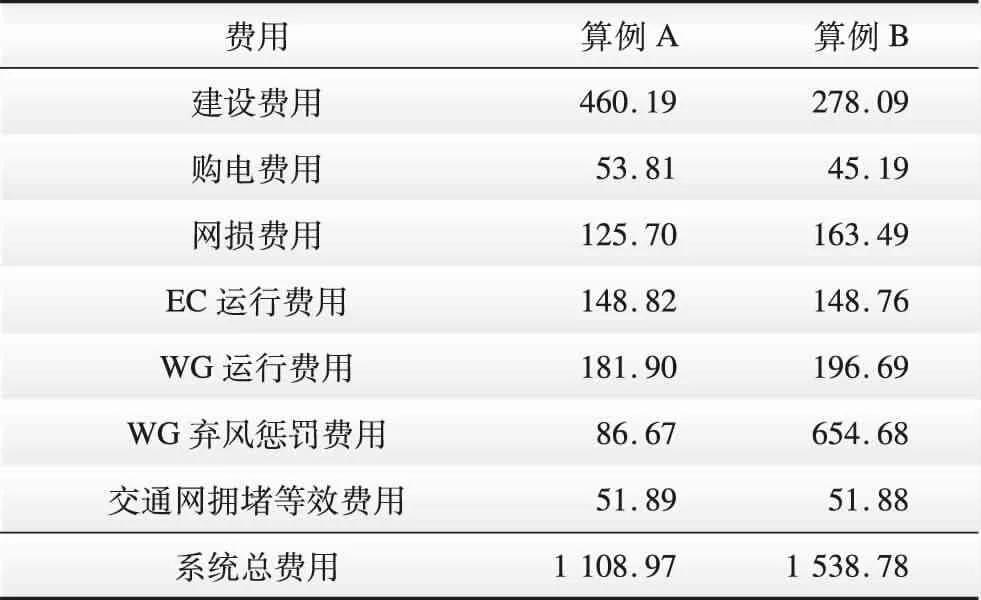
表2 算例A、B的经济费用情况Table 2 Economic costs of case A and case B 万美元
为了进一步说明引入冬-夏转移SHS的有效性和先进性,本文以CESS3为例分析SHS运行情况和系统弃风情况,作SHS动作与荷能情况和算例A、B的系统弃风情况图,分别如图5和图6所示。
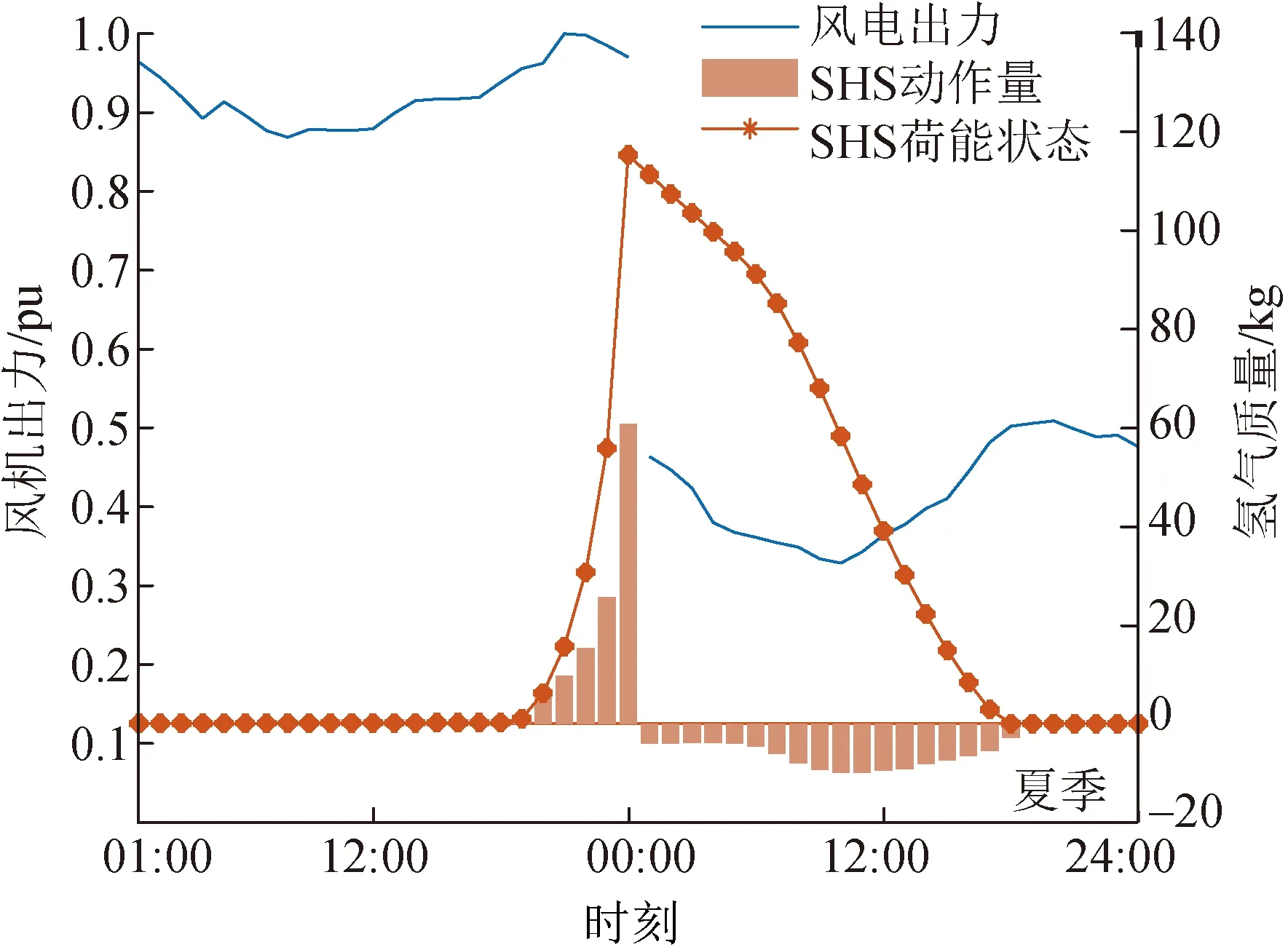
图5 季节性氢储动作量与荷能情况Fig.5 Chart of action quantity and state of energy of SHS
由图5可知,冬季时,20:00—24:00时段的风机出力水平处于全天的高水平阶段,此时过剩电能转化为氢能在SHS中存储;夏季时,储存的氢能逐步释放以满足系统需求,特别是07:00—17:00时段,风机出力水平低且负荷水平高,SHS释放氢能的速率有所增大。
由图6可知,冬季风机出力过剩将引起大规模的弃风。在引入SHS前(算例B),冬季全天均有弃风现象发生,冬季弃风量占比高达26.04%;在引入SHS后(算例A),系统仅在冬季20:00—24:00有少量的弃风,其余时段均能实现100%消纳,弃风比例仅占3.07%,冬季弃风现象有了明显的改善,从而保障了新能源汽车的绿电供应。

图6 算例A、B系统弃风情况Fig.6 Chart of wind power curtailment in case A and B
为了进一步验证多种耦合点位下SHS的建设先进性,本文将交通网与配网耦合节点进行偏移,点位情况与规划经济结果如表3所示。
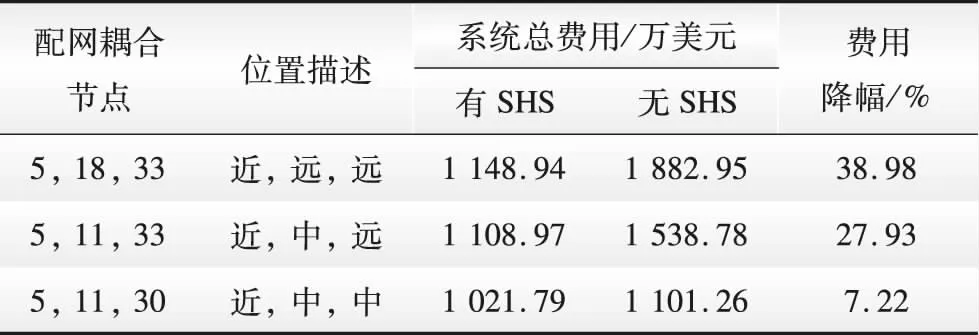
表3 多种耦合点位下的系统经济费用情况Table 3 System economic cost under multiple coupling points
分析表3可知,3种不同点位下考虑建设SHS均能降低系统的规划-运行总费用,进一步证明了SHS的建设先进性。此外,当CESS2耦合节点由中端向远处偏移时,投资费用降幅升至38.98%;当CESS3耦合节点由远端向中端偏移时,投资费用降幅缩小至7.22%。由此可见,当CESS耦合在供电能力越弱的配网节点时,建设季节性氢储的经济先进性越明显。
4.2 ES/HS/SHS配合情况分析
为系统性分析ES、HS、SHS在CESS中的配合情况,本文探讨多种储能组合情形下的系统投资情况,相关配置和经济结果如表4所示。

表4 多种储能组合情形系统总费用Table 4 Total economic costs of multiple storage combinations
分析储能两两配置情形(算例B、C、D)可知,缺少配置SHS、HS、ES任一类型的储能装置均会增加系统规划-运行总费用,其中算例B的涨幅(38.76%)相较于算例C(10.19%)和算例D(0.09%)最大,进一步证明了SHS相较于HS和ES在降低系统总费用中发挥的重要作用。此外,SHS和HS相配合(算例D)也能取得较好的系统经济性,仅略高于本文模型,表明HS能够在一定程度上替代ES的效用。
分析储能单一配置情形(算例E、F、G)可知,单一的储能配置方案经济效益较差,均不低于两两配置情形下的系统费用。其中,算例E的经济性最差,高达2 082.72万美元。由此可见,SHS对于HS和ES没有替代作用,说明只有长期储能形式(SHS)与短期储能形式(HS、ES)相互配合才更有利于系统经济运行。
分析无储能配置情形(算例H)可知,此时系统无可行的规划方案,表明配置储能装置对系统运行的必要性,侧面反映出在不考虑系统经济性的条件下,SHS、HS、ES 3种类型储能均能够增加系统灵活性以保障其安全运行。
4.3 分布式算法有效性分析
本文提出一种定制ADMM分布式求解方法以隔离供能系统和交通系统间敏感数据的传递,为直观说明分布式模型的有效性,表5汇总了集中式、分布式、分离式3种模型下的规划方案费用情况,其中分离式模型指交通网最优分布下的供能系统规划模型。
分析表5可知,集中式算法得到的规划方案最优,费用为1 078.78万美元;分离式算法求解结果最劣,费用为1 152.69万美元,同比增加6.9%,验证了将实际交通网考虑进能源系统规划中的必要性。与前2种方法相比,本文所提定制ADMM的优化总费用为1 108.97万美元,介于二者之间,说明了本文方法在隔离敏感信息的基础上能够有效实现供能系统和交通系统间的协同规划,通过适当增加交通部分运行费用以实现供能系统的规划-运行费用的降低,从而给出全局较优的规划方案。
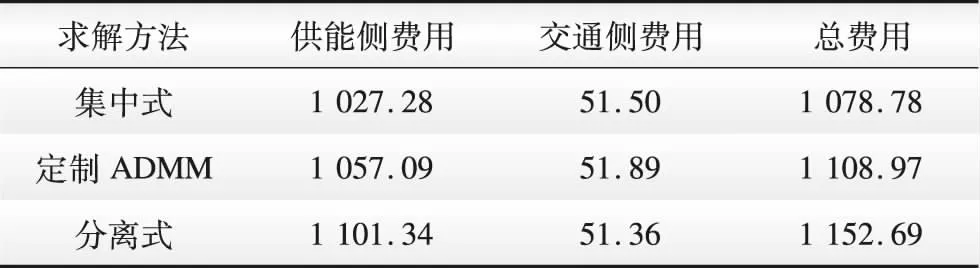
表5 不同规划模型的经济费用情况Table 5 Economic costs of different planning models 万美元
为了进一步说明采用定制ADMM对电-交耦合网络协同规划问题进行分布式求解的必要性,本文尝试利用标准ADMM直接对SP-EP和SP-TP进行分布式求解,算法收敛情况如图7所示。
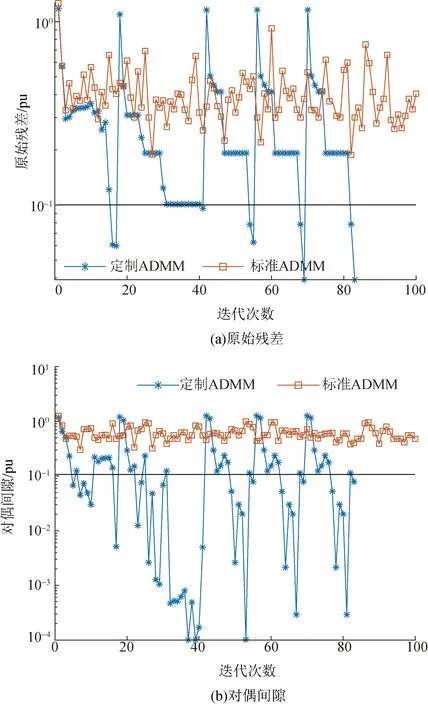
图7 定制ADMM和标准ADMM收敛情况对比Fig.7 Convergence comparison of tailored ADMM and standard ADMM
分析图7可知,采用标准ADMM的分布式求解方法在最大迭代次数100次后仍未达到收敛条件,不能得到合理的规划方案;本文提出的定制ADMM,由于进行的均是只含连续变量模型的分布式求解,故每次迭代均能在数代内快速收敛,具有良好的求解效果。
5 结 语
本文针对新能源汽车供能站规划工作中供能系统和交通系统间存在的信息壁垒,提出了一种基于ADMM的定制分布式求解方案。并且,探讨了冬-夏转移的季节性氢储、日常氢储、电储在电-氢联合供应的新型电力系统中的配合情况。经过算例仿真分析,可得出以下结论:
1)本文采用的冬-夏转移SHS能够降低冬季风机的弃风量,提升绿电实际送出比例,并且能够降低系统的规划-运行总费用,降幅高达27.9%。
2)在CESS中投资HS能够经济替代ES,并且采用长期储能(SHS)与短期储能(HS、ES)相配合的形式更有利于系统的经济运行。
3)本文所提定制ADMM能够实现供能系统和交通系统的协同优化,弥补了标准ADMM的收敛缺陷。
但本文仅考虑电力作为唯一的输入来源,而天然气也可作为制氢的重要能源形式之一,下一步将深入研究天然气供应商参与供能的分布式规划模型。

