考虑工业园区CHP机组动态约束的低碳经济调度

张磊,郑丹,卢天林,陈庆,叶婧,熊致知

(1.三峡大学电气与新能源学院,湖北省宜昌市443002；2.新能源微电网湖北省协同创新中心(三峡大学),湖北省宜昌市 443002)

0 引 言

大型零碳工业园区根据产业空间聚集来合理配置生产要素，逐渐成为我国工业企业发展的新型模式。由于工业生产需要，园区通常会配备热电联产机组(combined heat and power，CHP)来满足供电与供热需求[1-2]，构成工业园区电热耦合系统(industrial park electric-heat coupling system,IPEHS)。然而CHP机组供热需求下其刚性电出力限制了机组本身的可调度性[3-4]。这一突出现象给工业园区(特别是高能耗、高排放的大型化工业园区)低碳化运行带来了巨大挑战[5]。

近年来，CHP机组通过控制方法在满足电热耦合运行特性的基础上实现了机组电出力的快速调节[6-9]，从而使得CHP机组具有参与电网调频辅助服务的能力[10]，有效提升了园区清洁能源的消纳水平。现有含CHP电热耦合系统优化调度模型通常采用运行区域或者顶点凸组合法建立CHP运行约束[11](静态约束)，该方法建立的约束简单清晰，且易于实现，但是无法反映机组的实时运行状态，难以评估其运行安全性与稳定性。文献[12-13]采用机理建模，建立微分方程形式的CHP机组运行约束(动态约束)，该约束包含了机组各运行单元的主要变量，能够反映机组运行过程中各变量的实时状态。然而，在现有研究下，并未在调度过程中考虑CHP机组的运行动态约束，不利于实时掌握机组运行状态，增加了运行风险。因此，需要将CHP机组运行动态约束纳入到调度中考虑。

考虑CHP机组运行动态约束的IPEHS调度问题是一个含微分代数方程(differential algebraic equation,DAE)约束动态优化问题。对于该DAE优化问题，常规方法是将其离散转化为非线性规划(nonlinear programming,NLP)问题进行求解[14-16]。序贯法[17]求解动态优化问题时将原问题分为模拟层和优化层，模拟层采用初值方法求解DAE，计算灵敏度信息传递给优化层；优化层求解小规模NLP，将更新后的变量送入模拟层，两层交替迭代，构成序贯求解算法。该方法易于实现，但是灵敏度计算量大，求解时间较长。采用联立法将优化模型中的所有变量同时离散，统一求解，能够很好地避免复杂灵敏度信息的计算问题。同时通过正交配置法对模型进行离散，在一定程度上提高了求解效率[18-21]。但是随着系统规模增加，联立法容易形成“维数灾”，不利于优化问题快速求解[17]。

针对上述问题，本文首先建立考虑CHP机组动态约束的工业园区电热耦合系统低碳经济调度优化模型。该模型以考虑碳交易过程的园区最优成本为目标，建立园区各出力单元模型，采用多场景技术对风电出力、电负荷、热负荷随机性进行描述。然后基于序贯法框架，将调度优化模型分为模拟层和优化层。模拟层采用基于有限元正交配置法的离散方法求解DAE，优化层采用改进自适应差分进化算法求解NLP问题。算例结果表明有限元正交配置法能够以较少的离散点数获得较为精确的结果，提升求解效率。具备快速电出力调节能力的CHP机组能够有效提升工业园区风电消纳能力，降低企业碳排放压力。

1 考虑CHP机组动态约束的IPEHS模型

IPEHS能够实现园区电能、热能的互补协同，提高能源利用效率，降低碳排放量，其结构如图1所示。园区CHP机组主要由锅炉、汽轮机(高、中、低)、发电机等部件构成，其主要承担园区电负荷；此外CHP机组生产的高温高压蒸汽通过换热站、热力网络满足园区企业供热需求。与此同时，园区引入了风电机组，以提升园区清洁能源比例，降低碳排放。IPEHS中各单元模型详述于后。

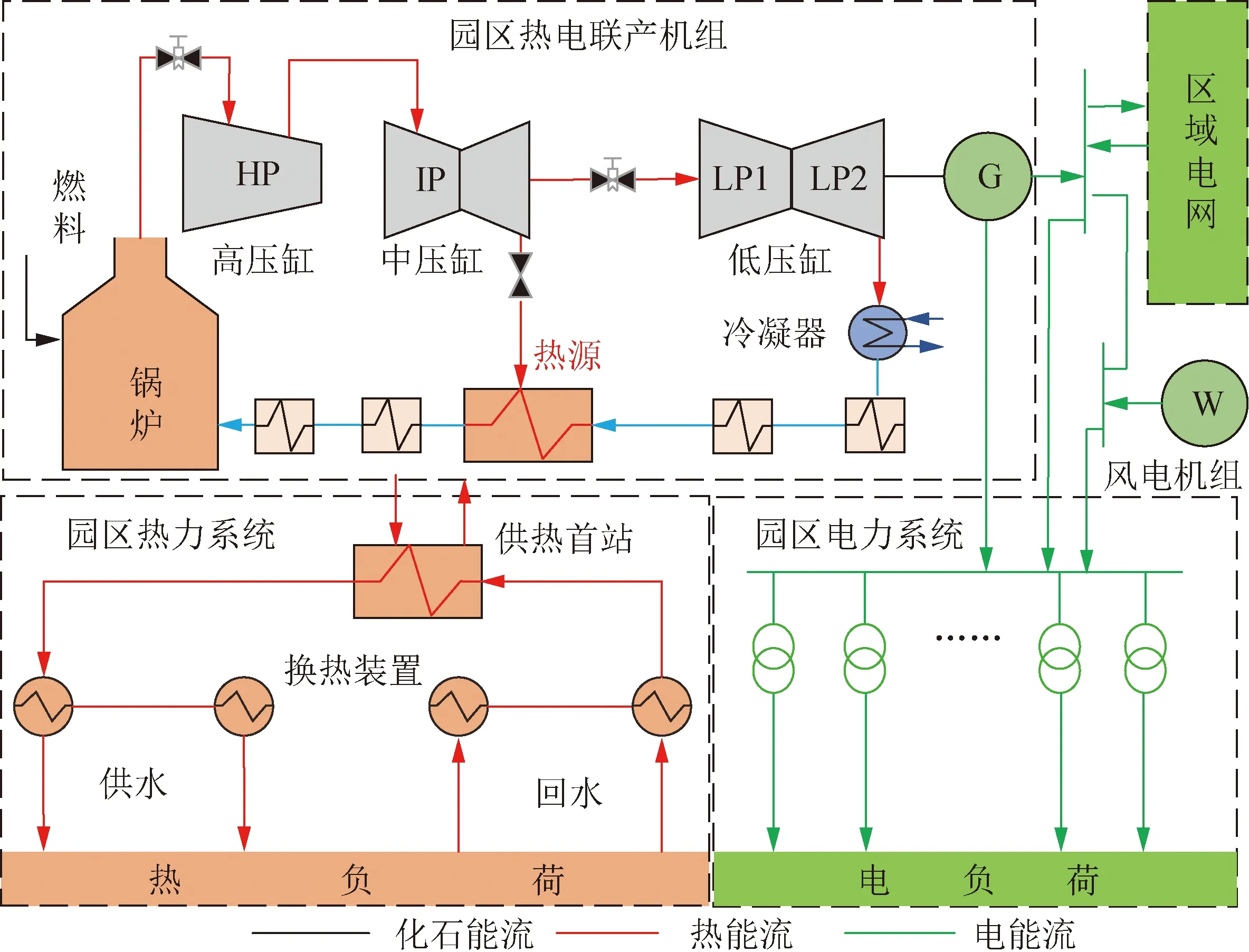
图1 IPEHS结构Fig.1 Structure of an IPEHS

1)热电联产机组模型。

抽汽式CHP机组是园区能量供应的主要来源，考虑CHP机组动态约束的非线性模型[12-13]如式(1)所示：

(1)

式中：uB为锅炉燃料进料流量；ε为煤制粉过程延时；Tb为制粉惯性时间；Tt为汽轮机惯性时间；t为时间参数；rB为锅炉燃烧率；Cb为锅炉蓄热系数；pd为汽包压力；uT为高压缸进汽调节门开度；p1为汽轮机一级压力；pm为主蒸汽压力；uH为供热抽汽调节蝶阀开度；pz为供热抽汽压力；Ph为机组发电功率；mh为供热抽汽流量；mx为循环水流量；τh为循环水回水温度；Ch为热网加热器蓄热系数；K1、K2、K3、K4、K5、K6、K7为常数；Ri为机组控制单元输入变量，包含uB、uT、uH；Mi为输出变量，包含Ph、pm、pz；ki、li分别为比例和积分参数；x为微分状态变量；u为控制变量；hU、hL为控制变量和状态变量不等式约束的上下限。

2)风电机组、电负荷、热负荷。

调度时期内风电机组出力与电、热负荷具有较强的随机性和不确定性，本文采用多场景技术对其进行建模，如式(2)所示

(2)

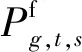
在上述模型的基础上采用拉丁超立方抽样进行场景生成，其步骤为：

1)将概率分为n个等概率区间；

2)将概率区间内的随机数Xi作为采样点；

3)逆变换概率分布函数Xi=f(xi)，获得采样点样本值xi。

获得风电机组的出力场景之后，由于场景数量较大，增加了运算负担，本文采用基于概率距离的快速前代消除技术进行场景削减。其步骤如下：

1)计算每个场景xi与其他场景xj之间的概率距离；

2)削减与xj最近的场景xi，并将削减的场景概率加到与其最近的xj上，确保所有场景概率之和为1；

3)重复上述步骤，直至剩余场景数达到设定值。

2 IPEHS低碳经济调度模型

2.1 优化目标

IPEHS低碳经济调度的目标是在调度时间内系统运行总成本F最小，如式(3)所示：

minF=FCHP+FW+FCA

(3)

式中：FCHP、FW、FCA分别为CHP机组运行成本、风电机组弃风成本以及碳交易成本。各成本定义如下所示：

(4)

(5)

(6)

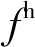
采用多场景技术对风电出力、电负荷、热负荷建模之后，共获得风电出力场景、电负荷场景、热负荷场景各5个，最终组合典型场景为125个。采用该方法后，目标函数式(3)转换为：

(7)

式中：N为削减后的场景数；ps为各场景的概率。

2.2 约束条件

1)CHP机组动态约束：式(1)。

2)风电机组出力需满足如下约束：

(8)

3)电力系统平衡约束：

工业园区内各调度时段内发电量之和与用电负荷保持平衡：

(9)

4)电力系统网络安全约束：

(10)

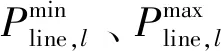
5)供热平衡约束。

对于园区供热系统，由于热力传输距离较短，且供热区域集中，忽略热网传输损耗，供热总量与热负荷保持平衡[22]：

(11)

式中：Qload,t为t时段的热负荷。

3 调度模型求解

3.1 序贯求解算法

考虑CHP机组动态约束的IPEHS低碳经济调度模型可以归纳为如下形式：

(12)

式中：x为状态变量；u为控制变量；p为代数变量；X为微分后的状态变量；J(·)为目标函数；c(·)为DAE等式约束；h(·)为不等式约束。

序贯法在求解模拟层DAE问题时，常用方法有改进欧拉法、隐式梯形积分等方法[23]。由于隐式梯形积分在求解过程中步长较小，计算速度较慢，为提高计算效率，本文在模拟层采用有限元正交配置法求解DAE，其具有离散点数少，计算精度高、稳定性好等优点。模拟层解出的状态变量以及灵敏度信息送入优化层，即可采用序列二次规划、内点法求解转换后的小规模NLP问题。本文在优化层采用自适应差分进化算法求解NLP。

3.2 基于有限元正交配置法的DAE求解

模拟层需求解如式(13)所示的DAE初值问题：

(13)

(14)

式中：h为单个有限元内配置点个数(插值阶次)；lj(τ)为x(t)的Lagrange基函数；xi,j为离散配置点；hi,j为单个有限元的时长；τ为时间参数。Lagrange基函数lj(τ)满足如下关系式：

(15)

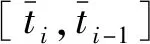
(16)

式中：pi,j为离散后的代数变量。

求解离散方程式(16)即可获得状态变量在离散点处的数值解，本文采用牛顿法求解有限元正交配置离散后的DAE。

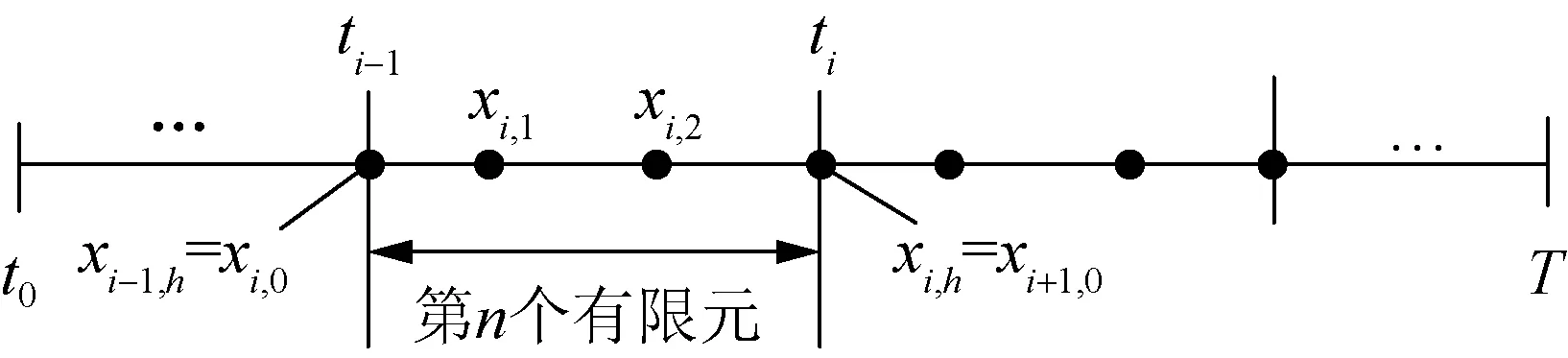
图2 Radau配置点Fig.2 Radau collocation point

3.3 基于自适应差分进化算法的NLP求解

针对优化层NLP问题，本文采用改进自适应差分进化算法(adaptive differential evolution,ADE)进行求解。改进ADE在求解过程中对变异系数进行动态更新，能够提升求解效率和全局搜索精度[24]。ADE自适应算子λ定义如下：

(17)

式中：l为当前迭代次数；lmax为最大迭代次数。

利用自适应算子对变异系数q进行动态更新：

q=q02λ

(18)

式中：q0为初始变异系数。

如图3所示，ADE算法求解步骤如下：

1)ADE参数设置，设置种群规模NP为200、变异系数q为0.3、交叉概率σ为0.5，最大迭代次数lmax为100；生成DAE初值。

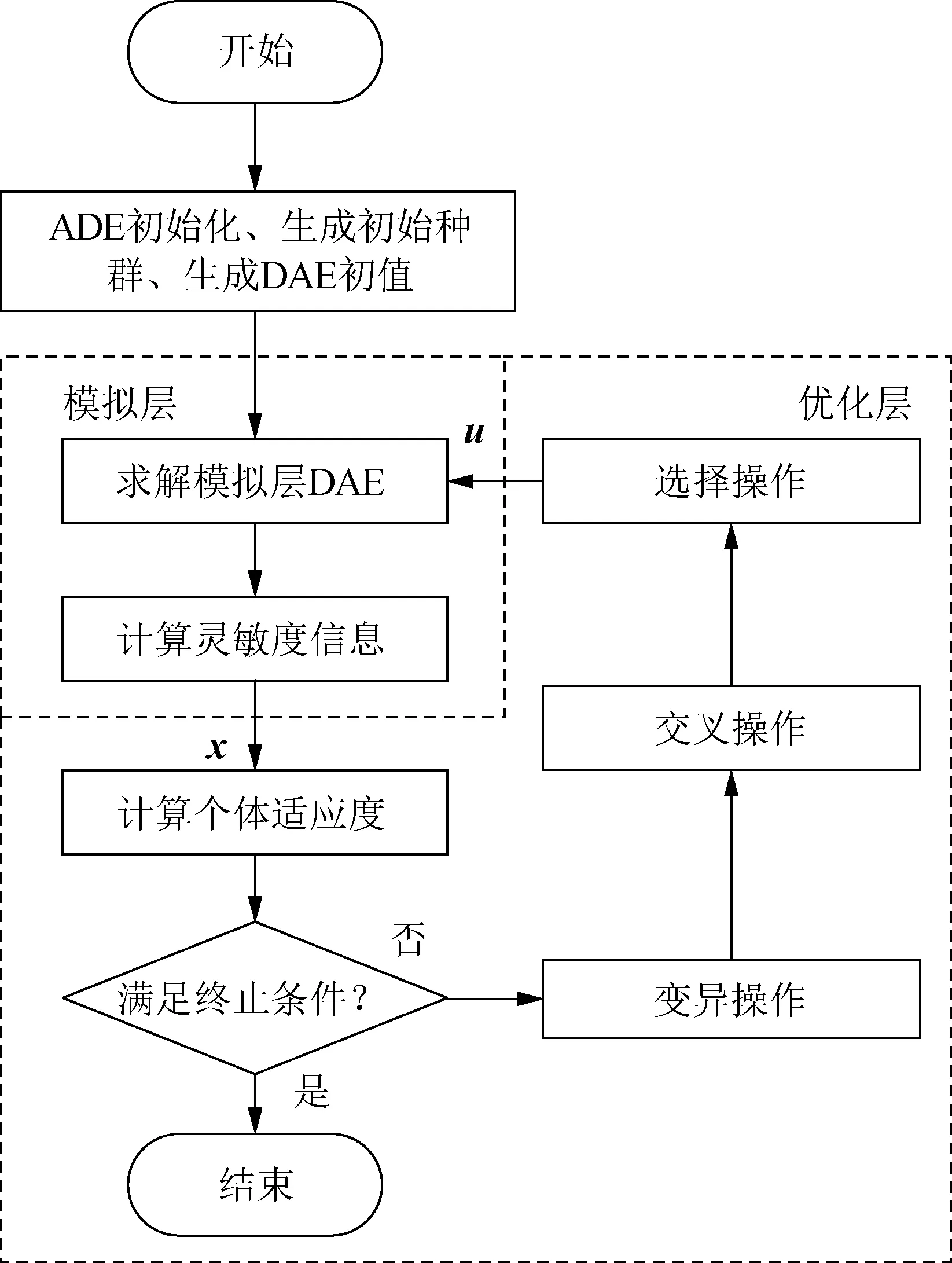
图3 改进ADE算法框架Fig.3 Algorithm structure of the improved ADE

2)求解模拟层DAE，并计算此时的灵敏度信息。

3)模拟层将状态变量值及灵敏度信息传递给优化层，计算当前个体适应度值。

4)判断是否满足终止条件。满足则输出当前最优成本；不满足则进行步骤5)。

5)变异操作。当前种群进行变异，如式(19)所示：

vi=xz1+q(xz2-xz3)

(19)

式中：vi为变异后的个体；z1—z3为[0,NP]范围内随机产生的整数；xz1、xz2、xz3分别为随机选择的个体。

6)交叉操作。对种群中个体与其子代变异个体进行交叉：

(20)

式中：ui,j为交叉后产生的个体；vi,j为变异后的个体；rand(0,1)表示产生0-1内的随机数。

7)选择操作。选择初始种群和步骤5)、6)中的优异个体，作为下一代种群，如式(21)所示：

(21)

式中：xi(l)为当前种群中的个体；ui(l)为交叉后产生的个体；J2[ui(l)]、J2[xi(l)]分别为当前个体与交叉个体对应的适应度值。

重复步骤2)—7)，直至满足终止条件，输出当前最优成本。

4 算例分析

本文采用改进的IEEE 14节点系统构建IPEHS，如图4所示，模型中节点5接入1台CHP机组，节点1、3、6、8接入风电场。模型参数、负荷及风电预测曲线见附录A。本文经济调度周期为30 min，调度时间尺度为5 min。

本文设置如下算例：

算例1：常规CHP机组参与调度(静态约束，如式(22)—(24)所示)，调度模型采用ADE进行求解。

(22)

Ph,i,t≥rQh,i,t

(23)

-RDΔt≤Ph,i,t-Ph,i,t-1≤RUΔt

(24)

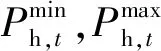
算例2：机组具备快速电出力调节能力(动态约束)，调度模型模拟层采用隐式梯形积分进行离散，优化层采用ADE进行求解。

算例3：机组具备快速电出力调节能力(动态约束)，调度模型模拟层采用有限元正交配置法进行离散，优化层采用ADE进行求解。

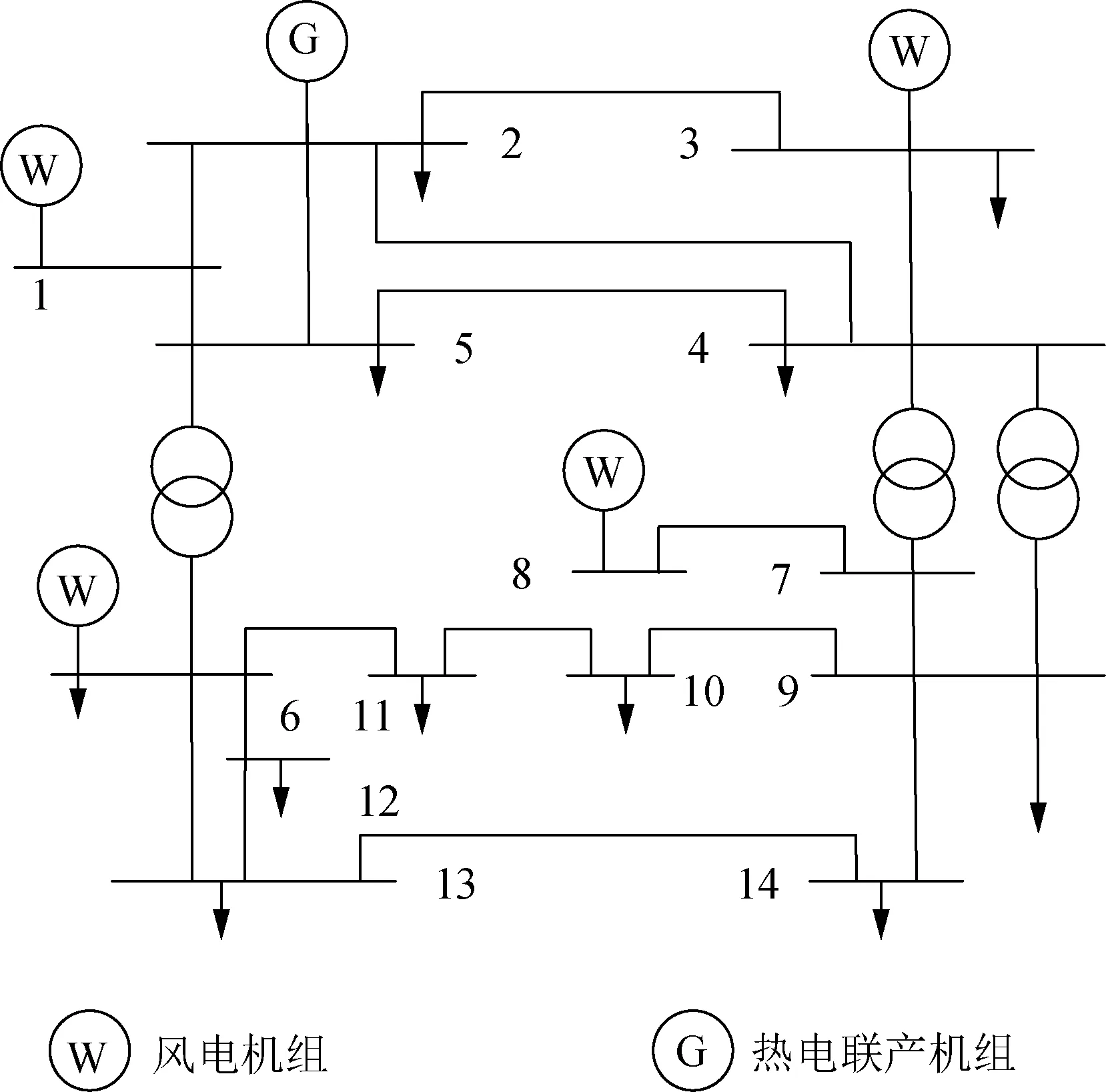
图4 改进IEEE 14节点系统Fig.4 Improved IEEE 14-bus system

4.1 计算结果分析

本节通过算例2和算例3对比分析采用不同的离散方式对求解效果的影响。算例2中隐式梯形积分方法由于数值稳定性较好，离散精度较高，本文将其作为基准方法，离散步长设置为0.01 s。算例2、3调度结果如图5所示，从图5中可以看出，不同离散方式下的机组出力基本相同。算例2、3计算结果如表1所示，算例2、3中的CHP机组出力成本、弃风成本、碳排放成本以及总调度成本非常接近，表明有限元正交配置法能够达到与隐式梯形积分方法相同的求解精度。对比求解时间可知：在成本相近的情况下，求解时间上有限元正交配置法具有较大的优势。由此说明，采用有限元正交配置法对本文DAE问题进行离散时，能够在保证求解精度的情况下降低求解规模，从而获得更高的计算效率。

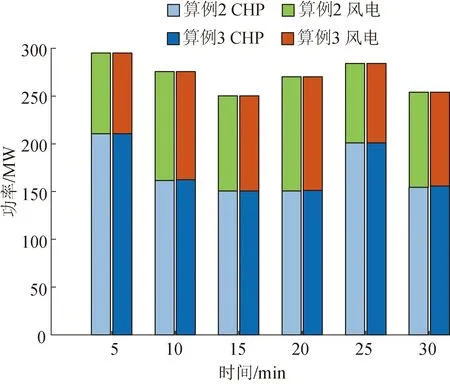
图5 算例2、3机组电出力Fig.5 Power output in case 2 and 3

表1 算例2、3计算结果对比Table 1 Comparison of calculation results in case 2 and 3

4.2 调度结果分析

具备快速电出力调节能力的机组和常规机组参与园区调度的成本如表2所示。在本文算例中，算例1的调度成本相比于算例3降低了6.68%，即1 119.45元。在各项调度成本中，相比于算例1，算例3 CHP机组成本降低了4.35%，风电弃风成本减少了168.17%，碳排放成本减少了5.16%。

表2 系统调度成本Table 2 Cost of system dispatching

算例1和算例3机组电出力如图6所示。在30 min的调度时间内，算例3在10、20、30 min时CHP机组的出力要显著低于算例1，与此同时，在这些时刻算例3风电机组的出力更多。其原因是，算例3 CHP机组具备更快的电出力调节速率，在不超出机组出力调节安全限制的情况下，相比于算例2中的常规CHP机组，算例3 CHP在5 min的调节时间内可调节的容量更大。在出力向下调节过程中，算例3 CHP出力下探更低，因此在整个调度时段内算例3 CHP出力更少，燃煤消耗量减少，碳排放量也更低，同时为风电上网腾出了更多空间。风电消纳能力及碳排放水平如表3所示，在整个调度时段内，相比于算例2，算例3碳排放量减少了41.58 t，风电消纳比例提高了8.47%。

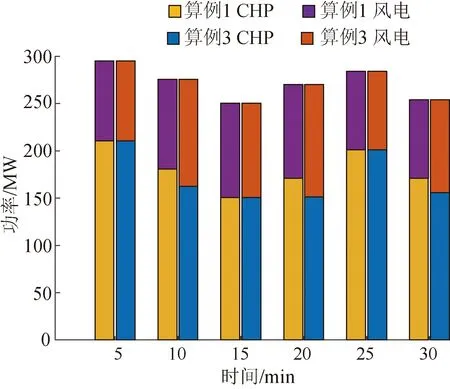
图6 算例1、3机组电出力Fig.6 Power output in case 1 and 3

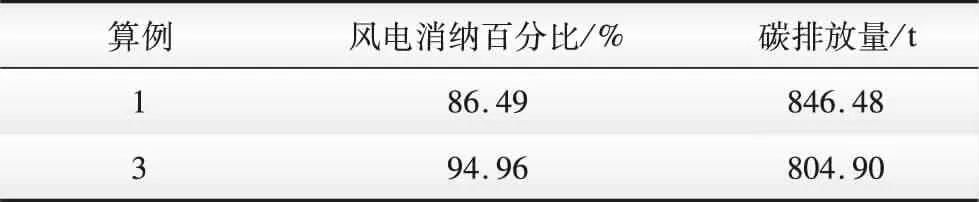
表3 风电消纳能力及碳排放水平Table 3 Capacity of wind power consumption and carbon emission

4.3 机组运行状态分析

算例2和算例3 CHP机组采用微分方程建立其动态运行约束，本节以算例3为例分析动态约束下CHP机组电出力、供热抽汽流量、主蒸汽压力的变化情况，如图7所示。

由图7可知，在调度过程中，算例3中CHP机组接收到负荷变化指令之后，能够迅速调整机组出力跟踪电负荷变化，这表明机组能够积极响应负荷信号，具备良好的辅助调频能力。在1、4、5等3个时段内，即使负荷变化比较剧烈，但是机组供热抽汽流量不仅能够跟随热负荷需求变化，超调量也在安全范围内(±50 t/h)；与此同时，主蒸汽压力的变化未越过安全限制(设定值为14.7 MPa，上下限±5%)。上述现象表明具备快速电出力调节能力的CHP机组采取动态约束描述时，能够实时掌握机组的运行状态，降低机组运行风险。

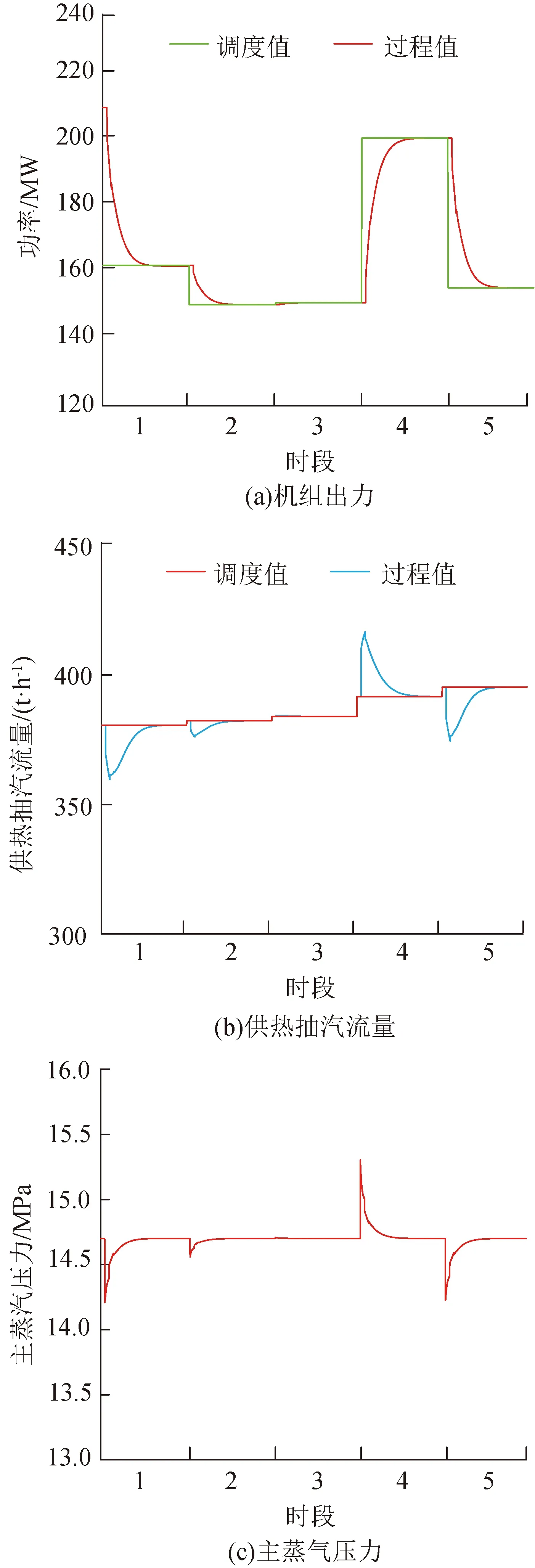
图7 算例3机组电功率、供热抽汽流量、主蒸汽压力变化情况Fig.7 Trend of CHP power output and heat extraction steam and steam pressure in case3

5 结 论

本文建立考虑CHP机组运行动态约束的工业园区电热耦合系统经济调度优化模型，提出一种基于序贯法框架的模型求解方法，通过算例分析，得出如下结论：

1)相比于隐式梯形积分方法，有限元正交配置法能够有效解决本文DAE优化问题的连续变量的离散问题，在保证本文优化问题求解精度的同时，能够降低优化问题的规模，从而提高优化问题的求解效率。

2)相比于常规CHP机组，具备快速电出力调节能力的机组使得工业园区调度系统应对负荷波动时在调度成本和风电消纳方面更有优势，有利于工业园区低碳化运行。

3)相比于CHP机组静态约束，动态约束能够精准描述机组出力调节过程、主蒸汽压力变化过程以及供热抽汽流量变化过程，有利于分析机组运行特性，调整机组运行状态，保证机组运行安全稳定。