改进混合粒子群算法求解旅行商问题

徐福强，邹德旋，章猛，罗鸿赟

（江苏师范大学 电气工程及自动化学院，江苏 徐州 221116）

0 引言

旅行商问题（TSP）是典型的NP-难问题［1］，也是经典的组合优化问题，故具有广泛的应用背景，如计算机联网、交通运输、电气布线、路线规划等［2］。获得高效的TSP 求解算法是组合优化领域的一个研究热点，目前求解TSP 的方法主要分为两大类。第一类是传统的精确算法，主要有分支定界法、线性规划法、动态规划法等［3］。但是随着TSP 中城市规模的增大，该类算法的求解能力显著下降。第二类是近些年来随着人工智能的发展而兴起的智能优化算法，主要有遗传算法（GA）［4］、蚁群算法（ACO）［5］、粒子群算法（PSO）［6］、模拟退火算法（SA）［7］等，现已广泛地应用于TSP 求解，并且取得了很好的效果。

由于PSO 具有搜索迅速、容易实现、参数设置简单等优点［8］，故对利用PSO 来解决TSP 的研究有着重要意义。但考虑到PSO 最初是用于连续型问题求解，而TSP 是离散型的组合优化问题。针对这个问题，近年来不断有学者提出了适用于解决TSP的改进PSO。例如，高尚等学者［6］结合遗传算法、蚁群算法和模拟退火算法的思想，提出用混合粒子群算法来求解TSP，并且在遗传算法的交叉和变异的策略选择上进行了详细的介绍，但其解决TSP 的问题规模太小，并未验证该算法在大规模TSP 上的实用性。邓伟林等学者［9］提出一种离散粒子群算法来解决TSP，重新定义了速度及其粒子位置的相关算子，并设计距离排序矩阵来指导粒子进行高效的全局搜索，但是其参数设置较为复杂，算法收敛速度较慢。裴皓晨等学者［10］提出一种引入混沌算子的改进混合粒子群算法优化来解决TSP，可使搜索的范围扩大，提高了搜索到更高质量解的概率，但在求解规模稍大的TSP时，解的质量明显下降。Wei等学者［11］将概率初始化策略和遗传算子引入到粒子群优化算法中，提出一种解决TSP 的改进混合粒子群算法，在算法迭代过程中节省了更多计算资源，增加了种群的多样性并提高了算法的收敛精度，但在解的质量和求解稳定性上还有不足。

针对以上所述的解决TSP 的各种改进粒子群算法的优缺点，本文提出了结合贪心策略［12］、动态学习概率、Metropolis 准则［13］和2-opt 局部优化［14］的改进混合粒子群算法。依据贪心策略对种群进行初始化可以得到更高质量的搜索空间，一定程度上保证了解的质量；加入动态学习概率来平衡粒子群算法中的个体学习和群体学习；在个体学习和群体学习的过程中采用Metropolis 准则来依一定概率接受劣解，不仅增加了种群多样性也提高了算法在搜索过程中跳出局部最优的能力；变异的部分采用2-opt 局部优化的策略可以消除路径中出现交叉的现象，增强局部搜索能力，并进一步提高全局解的质量。最后，通过Matlab 将本文改进算法和其他4 种智能优化算法在TSPLIP 中的8 个实例上进行了仿真测试，证明了本文改进算法在求解精度、解的稳定性上具有更好的表现，并且对大规模的TSP 也具有较好的求解能力。

1 旅行商问题描述

旅行商问题最早由Flood［15］在1956 年提出，是一个具有代表性的离散组合优化问题。可以描述为一个商品的推销员要去若干城市推销商品，随机选择某一个城市作为起点，从该城市出发，要求经过所有的城市并且只经过一次，最后再回到起点城市。也就是构成一个哈密顿回路［16］，关键在于找到一条满足条件的行进路线使得整个回路的路径长度最短。

从图论的角度来描述TSP［17］如下：设图G＝（V，E），这里V表示所有城市组成的顶点集，E是集合V中元素（城市）两两相连组成的边集，设每2个城市之间的距离记为则求解TSP 的数学模型可表示为：

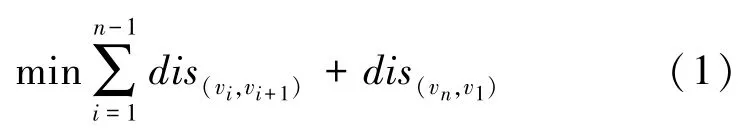
式（1）中的第一项是对从1到n个城市计算最短的路径距离和，式（1）中的第二项是计算第n个城市回到第一个城市的距离，这2 项相加构成一个完整的回路路径长度。

2 算法分析

2.1 粒子群算法

PSO 是一个由Kennedy 和Eberhart 在1995 年提出的群体智能优化算法［18］。其基本思想是先随机初始化一群粒子，每个粒子都具有速度和位置以及由目标函数决定的适应度值这3 个属性，再引入个体极值和群体极值的2 个概念。在每次迭代过程中，根据式（2）和式（3）来更新每个粒子的速度和位置，然后计算适应度值，并根据目前的适应度值来更新个体极值和群体极值，再经多次迭代，搜索到目标函数的最优解。标准PSO 的速度与位置的更新公式如下：

2.2 遗传算法

遗传算法是由Holland 教授［19］在所著的《自然界和人工系统的适应性》中首先提出的。是一种受到生物界自然选择和自然遗传现象启发的随机搜索算法。算法模仿自然遗传现象中的繁殖、交叉和基因突变的情况［20］，根据一定的标准来进行选择和保留较好的候选解，此后再经过不断地重复迭代，直至找到最优解或者满足终止条件为止。

2.3 解决TSP 的混合粒子群算法

混合粒子群算法就是把遗传算法和粒子群算法进行了融合，通过遗传算法的交叉操作和粒子群算法中的个体学习和群体学习来对每代粒子个体进行优秀子代的产生和遴选；在此基础上将通过遗传算法的变异来替代实现粒子群算法中的位置更新操作，经多次迭代后找到TSP 的最优解。近年来，经过较多学者研究和大量的实验仿真结果充分地证明了混合粒子群算法的有效性和先进性。但是其在求解TSP 的精度和稳定性方面还有一定的提升空间，并且对大规模TSP 的求解能力较差。

3 算法改进

3.1 基于贪心策略的种群初始化

智能群体优化算法一般是随机生成初始种群，这样容易使初始种群个体的适应度值与研究需要的最优解的适应度值出现很大的偏差。造成算法收敛速度的降低和运行耗时的增加，还会导致解的质量下降、甚至增加了算法陷入局部最优的可能。

本文采用基于贪心策略的种群初始化来有效地保证初始搜索空间的质量。具体方法是按照在TSP中两城市间距离最短的思想来依次选定一个起始城市，然后在剩余城市中选取与上个选定城市距离最近的城市作为下一个城市，循序重复操作直至最后一个城市。这样得到的城市序列作为改进混合粒子群算法的初始解，在一开始迭代的时候就具有较好的适应度值，有利于加快算法的收敛速度，提高算法求解精度。

3.2 加入动态学习概率

在粒子群算法中通过个体学习和群体学习来更新粒子的速度，个体学习有利于拓展粒子的搜索空间，群体学习有利于粒子朝全局做最优搜索。结合解决TSP 的具体情况，本文采取加入动态学习概率的方法调节与个体最优交叉及与群体最优交叉的进行，来更好地平衡个体学习与群体学习。动态学习概率的数学定义式如下：

其中，iter表示目前的迭代次数，itermax表示算法设定的最大迭代次数。

通过式（4）可知，随着迭代的不断进行，p1会不断变大，当取一个0～1 之间的随机数大于p1时，与个体最优交叉，即个体学习；否则，与群体最优交叉，即群体学习。所以，算法迭代搜索的前期个体学习的概率更高，增加了种群的多样性；到了算法迭代的后期，群体学习的概率更高，倾向于和群体最优进行交叉，利于算法的全局收敛。

3.3 采用Metropolis 准则接受劣解

由于混合粒子群算法在解决TSP时，容易陷入局部最优而导致算法收敛不到最优解。所以本文改进算法在个体学习和群体学习中采用Metropolis 准则来依概率p2接受劣解，从而在一定程度上丰富了种群粒子的多样性，提高了算法跳出局部最优的能力。概率p2的数学表达式如下：

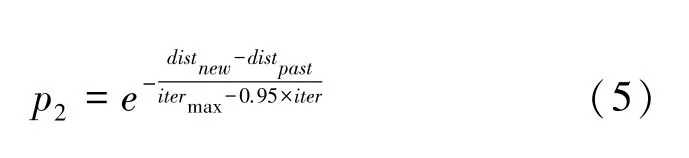
其中，distnew表示经过个体学习或群体学习产生的新城市序列对应的路径长度；distpast表示之前的旧城市序列对应的路径距离；随着迭代的进行，itermax-0.95× iter的值在不断减小，根据指数函数的特点，p2的值在逐渐减小，所以迭代到后期，接受劣解的可能性就不断降低，保证了算法的收敛性。当distnew ＜distpast时，直接用新城市序列替换旧城市序列，实现算法朝距离最短的城市序列方向搜索。否则，在个体学习和群体学习中依据rand ＜p2的概率来接受distnew ＞distpast的城市序列。并且如果distnew -distpast的值较小，也就意味着新解和旧解对应路径距离相差得小，p2值反而越大，则rand ＜p2的概率越大，接受该劣解的可能性就更大，并且该劣解经过此后的2-opt 局部优化得到更短路径的可能性也越大。

3.4 2-opt 局部优化

TSP 中很容易出现路径交叉的现象，并且路径一旦有交叉势必会导致整个路径距离的增加，故而消除交叉现象的发生也是解决TSP 的重要一步。考虑到2-opt 局部优化的耗时性，本文对个体学习和群体学习后的粒子适应度值进行升序排列，取适应度值从小到大且20%种群规模数量的粒子进行2-opt局部优化。2-opt 局部优化操作示意如图1 所示。

图1中，图1（a）表示原路径，是经过个体学习或群体学习得到的目前搜索到的最好的城市序列：A→B→C→D→E→F→G→H→A，可以直观地看出城市B和城市C及城市F和城市G之间有路径交叉的现象；再观察图1（b）中的新路径，就是把城市B和城市G的位置进行了调换，同时把原来城市B和城市G之间的城市序列顺序进行了倒置。新的城市序列为：A→G→F→E→D→C→B→H→A。显而易见，之前的交叉现象被消除了，路径的长度也缩短了，故证明了2-opt 局部优化的有效性。

图1 2-opt 局部优化操作示意图Fig.1 Schematic diagram of 2-opt local optimization operation

本文采取2-opt 局部优化作为本文改进算法中的变异操作，同时也实现粒子群算法中综合个体学习和群体学习后的位置更新操作。经过2-opt 优化后，比较选择更短的城市路径距离对应的城市序列，使得算法朝着全局最优搜索。

3.5 改进混合粒子群优化算法解决TSP 的步骤

步骤1加载TSP 实例和计算城市间距离。

步骤2算法初始化，包括种群的初始化，结合城市间的距离来基于贪心策略得到较高质量的初始种群，同时设置本文改进算法的最大迭代次数，作为算法结束的标志条件。

步骤3计算粒子适应度值，并确定个体最优和群体最优。

步骤4根据动态学习概率p1来进行学习策略的选择，如果随机数大于p1，则选择个体学习，与粒子个体最优进行交叉，否则选择群体学习，与群体最优进行交叉，并且在个体学习和群体学习中加入了Metropolis 准则，依概率p2来接受劣解。

步骤5对经过个体学习和群体学习的种群进行2-opt 局部优化操作，消除路径交叉的情况，搜索更优解。

步骤6判断是否达到算法终止条件，本文为设定的最大迭代次数，如果达到，输出最优解及对应的最短路径长度，否则返回步骤3，重复执行，直至满足算法终止条件。

本文改进混合粒子群算法流程如图2 所示。

图2 改进混合粒子群算法流程图Fig.2 Flow chart of improved hybrid particle swarm optimization

4 仿真实验及分析

4.1 仿真实验基础

根据以上分析，为了验证本文改进混合粒子群算法解决TSP 的可行性与有效性，将混合粒子群算法、GA、ACO、SA 及本文改进混合粒子群算法在Matlab 仿真软件上对TSPLIB 中的8 个不同城市规模的实例进行测试。

本文仿真实验环境配置如下：硬件方面使用AMD Ryzen 7 5800H 3.2 GHz CPU，16 G RAM 的计算机；软件环境基于Windows 10，Matlab R2019a。

本文仿真实验选用了TSPLIB 中8 个不同城市规模的实例，从小到大分别是Oliver30，eil51，st70，eil76，eil101，ch150，pr226，pcb442。混合粒子群算法参数设置：种群规模取1 000，最大迭代次数取200，与个体最优交叉的概率取0.5，与群体最优交叉的概率取0.5，变异的概率取0.3；GA 参数设置：种群规模取1 000，最大迭代次数取200，交叉概率取0.7，变异概率取0.2；ACO 参数设置：蚂蚁数量等于TSPLIB 实例中的城市个数，最大迭代次数取200，信息素重要程度因子取1，启发函数的重要程度因子取5，信息素挥发因子取0.2；SA 参数设置：初始温度61 ℃，结束温度3 ℃，温度衰减系数取0.985，马尔科夫链长度取TSPLIB 实例中城市个数的100倍；本文算法参数：种群规模等于TSPLIB 实例中城市个数，最大迭代次数取200，动态学习概率为p1，Metropolis 准则中接受劣解的概率为p2，选取进行2-opt局部优化的粒子个数为种群规模的20%。

4.2 实验结果与分析

经过以上分析，将5 种算法在8 个TSPLIB 实例上独立运行30次，记录每次的运行结果。对各算法在每个TSPLIB 实例上运行得到的30 个结果进行处理，找到最优解、最差解，计算出平均解，再结合TSPLIB 实例的已知最优解［21］，根据式（6）计算出平均偏差率。具体见如下：

5 种算法的实验结果见表1。表1中，测试实例下面的括号中数值就是目前对应TSPLIB 实例的已知最优解。由表1 可以发现在解决实例Oliver30时，各算法搜索到的最优解都很接近已知最优解，并且平均偏差率都很小，说明各算法搜索的稳定性都还不错，其中SA 的效果最好，略优于本文改进算法；而随着TSP 规模的增加，各算法搜索到的最优解开始慢慢与已知最优解的偏差增大，其中混合粒子群算法和GA 体现得尤为明显，当TSP 规模到100 及以上时，求解的质量很差，故而混合粒子群算法和GA 对ch150、pr226、pcb442 这3 个实例的实验结果直接舍弃；虽然在本文仿真实验中ACO 和SA求解了大规模TSP 的解，但是观察表1 可知，ACO和SA 的最优解和偏差率都比本文改进算法的结果大，表明了本文改进算法对于解决大规模的TSP 具有更好的适应性和明显优势。

表1 算法实验结果Tab.1 Experimental results of the algorithm

为了更加直观地了解5 种算法解决TSPLIP 实例的过程情况，本文绘制出了5 种算法解决eil51、st70、ch150、pcb442 这4 个具有代表性的实例上的迭代曲线，如图3～图6 所示。观察图3 和图4 可以发现，本文改进混合PSO 的初始解就具有很大优势，并且收敛的速度要比其他4 种算法明显更快，搜索到最优解的迭代次数更少，凸显出算法的寻优能力较强。观察图5 和图6 可知，当TSP 的规模较大时，本文提出的改进混合PSO 仍然具有很强的寻优能力。与ACO 和SA 相比，求解TSP 的质量更高，并且较少的迭代次数就可以搜索到最优解，表明了本文改进算法的适应能力强和求解精度高。为了直观地考察本文改进算法的求解效果，根据上述分析做出对应的求解到的最优路径图如图7～图10所示。

图3 eil51 迭代曲线图Fig.3 Iteration curve of eil51

图4 st70 迭代曲线图Fig.4 Iteration curve of st70

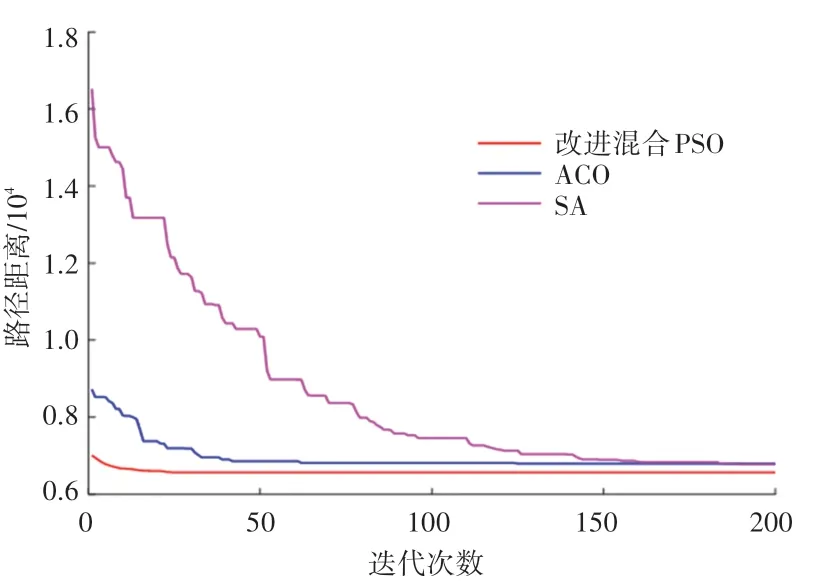
图5 ch150 迭代曲线图Fig.5 Iteration curve of ch150

图6 pcb442 迭代曲线图Fig.6 Iteration curve of pcb442

图7 eil51 最优路径图Fig.7 Optimal path of eil51

图8 st70 最优路径图Fig.8 Optimal path of st70

图9 ch150 最优路径图Fig.9 Optimal path of ch150

图10 pcb442 最优路径图Fig.10 Optimal path of pcb442

5 结束语

本文提出了一种改进混合粒子群算法来解决旅行商问题，利用基于贪心策略的种群初始化很好地保证了算法搜索空间的质量；在算法的搜索过程中加入动态学习概率来选择个体学习或群体学习，并在每个学习中引入Metropolis 准则来依一定概率接受劣解，既能增加种群粒子的多样性，也能提高算法跳出局部最优的能力；再将经过个体学习和群体学习得到的城市序列进行2-opt 局部优化，有效地消除了城市路径间出现交叉的现象，并且较好地保留更短的路径及对应的城市序列，保证了算法朝着全局最优的方向进行收敛，提高了算法求解的精度。最后和其他4 种智能优化算法在Matlab 软件上对TSPLIB 的8 个不同规模的实例进行了测试，仿真结果表明了本文改进算法的求解精度更高，算法的稳定性更好，并且更加适应于大规模TSP 的求解。