基于灰狼优化的V-detector 检测器分布方法

郑德强

（佳木斯大学 信息电子技术学院，黑龙江 佳木斯154000 ）

0 引言

5G 商用时代的全面到来意味着互联网信息数量将迎来指数型爆炸，互联网安全随即变得更加重要。入侵检测系统（Intrusion Detection System，IDS）作为一种主动防御的网络安全技术，长期以来一直将其视作防火墙之后的第二道防线。通常情况下，入侵检测是通过对网络流量以及计算机系统日志等进行扫描，发现危险信息及漏洞。常见的入侵检测技术有基于人工免疫、统计分析以及神经网络［1］等技术的检测方法。其中，基于人工免疫的入侵检测作为一种受生物免疫系统启发而提出的入侵检测技术，受到了国内外学者的广泛关注。

作为人工免疫入侵检测技术的核心算法，否定选择算法（Negative Selection Algorithm，NSA）具有无须先验知识，只用少量正常样本便能检测无限数据的特点［2］。由于现代网络信息数据流的特点，否定选择算法已经从二进制否定选择算法发展为现在的实值否定选择算法（Real-value Negative Selection Algorithm，RNSA）。由于否定选择机制的特殊性，算法生成的检测器会存在检测黑洞或者冗余现象。针对这一特点，Zhou 等人［3］提出了V-detector 算法。

V-detector 算法应对检测冗余现象优先生成半径较大的超球体检测器，针对覆盖黑洞问题生成半径较小的检测器，这样有利于控制检测器的规模，提高了RNS 的精确性和时效性［4］。但是由于检测器分布的随机性和半径的不确定性也导致了检测器的高重叠问题，同时V-detector 算法不可避免地沿袭了否定选择算法存在的检测黑洞问题。

针对V-detector 存在的问题，文献［4］利用异常检测中容易被忽略的非自体元素，将非自体元素进行非自体区域的检测以及用来生成检测器。这样保证了新生成的检测器落入检测黑洞的概率大大减小，提高了检测黑洞的覆盖率以及检测器的质量。文献［5］通过修改检测器的生成规则以及对检测器进行优化，同时采用记忆检测器和成熟检测器两种组合，减少了计算量和存储空间的大小，提高了检测率，改进了无线传感器网络入侵检测模型。文献［6］通过与克隆选择算法（Clonal Selection Algorithm，CSA）的结合，引入定距变异的思想。提升了检测率和覆盖率，但是由于自体集的庞大，导致算法较为耗时。文献［7］受容差粗糙集启发，提出了一种新的检测器构造方法，将其运用到Vdetector 算法中，提高了检测效率。

鉴于此，本文引入灰狼优化（Grey Wolf Optimizer，GWO），将其运用到检测器的生成中，并对检测器的分布进行优化，提高检测器的覆盖率。基本思想为：通过GWO 算法对随机生成的检测器分布位置进行优化，优先生成较大半径检测器，同时标记出新的检测器，保证覆盖率。达到理想覆盖率后合理调整适应值，进行检测黑洞的覆盖。实验结果表明，该算法能显著提高检测器的分布覆盖率和减少检测黑洞，同时运行时间也较为理想。

1 相关工作

1.1 V-detector 算法

由于检测器的半径就是匹配的阈值，所以检测器的半径可以作为人工控制的因素来进行调配。V-detector算法针对实值否定选择算法存在的检测器数量庞大的问题，优先使用半径较大的检测器先覆盖非自体区域；针对检测漏洞问题，提出使用半径小的检测器去覆盖检测黑洞。这样大大提高了检测器的质量，但是检测器的分布位置仍是随机产生的，依然有优化的空间。因此，可以使用灰狼优化算法对检测器的落点位置进行优化，使检测器分布更加合理。

1.2 灰狼优化算法

研究可知，灰狼优化算法就是从灰狼群体捕食行为启发得到的［8］。灰狼群体有一个非常严格的社会统治阶层。灰狼种群的等级如图1 所示。

由图1 可知，领导层通常是一雄一雌，叫做α，对应到算法，α即为算法中的最优解。处于第二层的是β狼，β狼属于从属狼，也是算法中的次优解。第三层的δ狼、也即算法中的第三优解。处于最底层的是ω狼，ω为剩余的所有解。

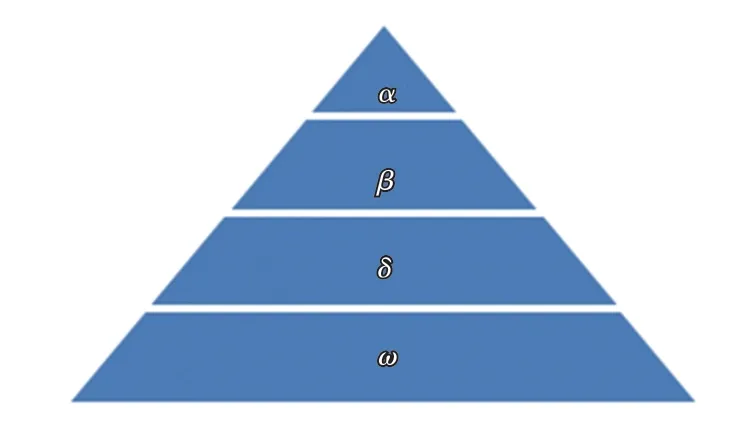
图1 灰狼种群的等级制度Fig.1 Gray wolf population hierarchy

灰狼算法的数学模型可描述为：

灰狼群体的狩猎过程通常由α狼指挥，β狼和δ狼偶尔也会参与狩猎指挥。由于在实际函数优化过程中，问题最优解（猎物位置）往往是不可知的，为了模拟灰狼的捕猎过程，规定α、β和δ对猎物的潜在位置有更好的了解。每次迭代都会得到当前最优的3 个解的同时，强制其他灰狼个体（包括ω）根据最优位置来更新自己的位置。此处需要用到的数学公式可写为：

2 本文算法

2.1 改进灰狼优化算法

针对灰狼算法的改进有很多，例如种群初始化方式、修改位置更新方程、重新设定距离控制参数及收敛因子等，为了应对形态空间的复杂性，本文引入混沌初始化和莱维飞行来增强灰狼优化算法的寻优能力。

2.1.1 混沌初始化

灰狼种群的初始化十分重要，初始灰狼优化算法的迭代种群都是随机产生，随机产生的种群容易陷入局部最优［9］。对应到检测器生成过程，局部最优会导致达到理想检测率所需检测器数量增加，增加运算资源的消耗。因此本次研究中引入混沌机制，用于群体的初始化。

混沌现象是一种非常普遍的非线性行为，表现出运动随机的同时也存在着一定的内在规律性，因此也被称为貌似随机的不规则运动。混沌机制具有非线性、非周期性、遍历性等特点，这些特点正有利于克服群体智能算法初始解的盲目性。实验证明［10］，使用混沌机制进行种群初始化会有利于优化算法进行更有效的全局搜索。

混沌机制有很多映射模型，常见的有Logistic 映射、PWLCM 映射、Singer 映射等，本文选取Logistic映射模型［11］进行种群初始化。其数学模型如下：

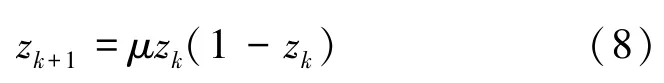
其中，μ可称为分支参数，通常取值为4；zk为混沌变量。

2.1.2 莱维飞行

由于自体形态空间的复杂性，实际搜索中难免出现寻优漏洞，导致检测黑洞的产生。为了更好地进行全局寻优，本文算法引入莱维飞行［12］来改进灰狼算法的寻优过程。

莱维飞行得名于其搜索的运动轨迹，即在随机行走的过程中会有一定的概率实现大跨步，将其与步长分布没有重尾的随机行走相比，该运动轨迹像飞行一样。

简而言之，莱维飞行是一种以短距离随机搜索为主，一定概率长距离搜索为辅的搜索行走方式。这种搜索方式可以使得算法在复杂的自体空间搜索变得更加全面，减少检测黑洞的产生和避免寻优算法陷入局部最优。

莱维飞行位置更新公式［13］为：

由于莱维飞行的实现至今未有一个统一的形式，所以本文采用Mantegna 算法模拟，Mantegna 算法数学表述如下。

步长s计算公式为：

其中，μ、ν为正态分布，即：

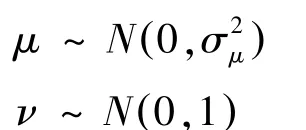
具体地：

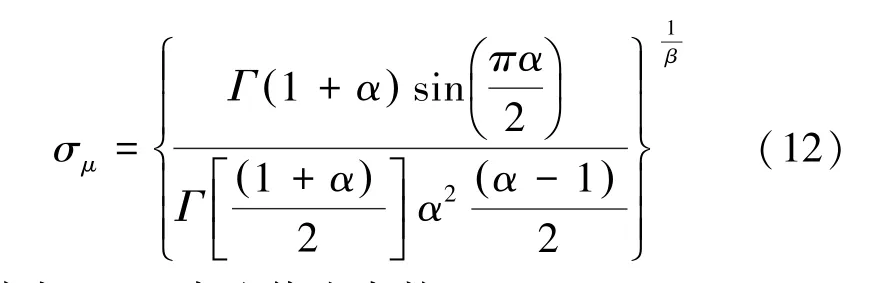
其中，α通常取值为常数1.5。

2.2 IGV-detector 算法

人工免疫入侵检测算法的目标是生成的检测器拥有尽可能大的覆盖率和尽可能小的重叠率，很明显优先使用较大半径的检测器有利于得到更大的覆盖率。

对于检测器j，假设pk是离其最近的检测器的中心点，于是就有：

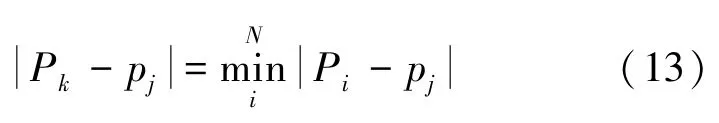
本文自体和检测器以及检测器和检测器之间的亲和力计算仍然采用欧氏距离，即｜ Pk -pj ｜和｜Pi -pj ｜的计算公式见如下：

如果此时存在检测器i使得｜Pi -pj ｜≤Ri，即该检测器落在了自体区域，则该检测器视为无效检测器。此时得到检测器j的半径：

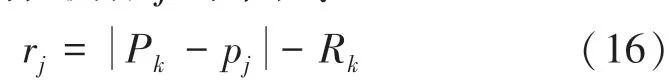
式（16）保证了每次生成的检测器都有尽可能大的半径，同时和自体不会有重叠。通过公式（15）和公式（16）得到检测器的半径rj依赖于检测器的落点pj。由于落点位置的无导数性质，可以使用灰狼算法来优化检测器的pj，同时适应值被定义为检测器的rj大小。对应于灰狼算法也就是半径较大的候选检测器个体等级更高，每次迭代完成后头狼α的位置即为相对最优检测器的位置，α值即为该检测器的半径大小。

至此，研究给出了IGV-detector 算法流程如图2所示。改进灰狼算法优化后的IGV-detector 算法步骤详见如下。

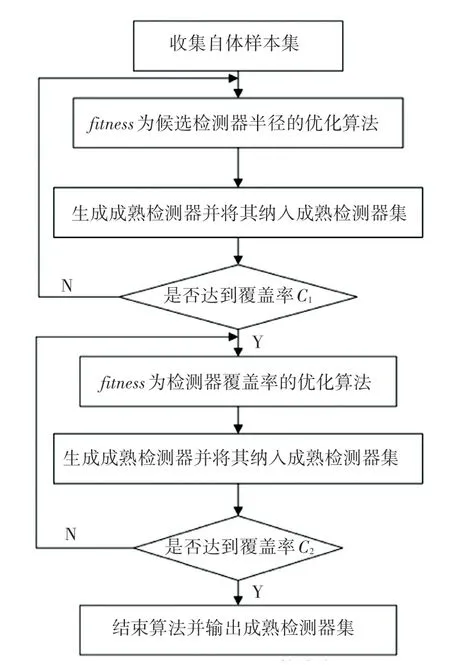
图2 IGV-detector 算法流程Fig.2 IGV-detector algorithm flow chart

Step 1设定生成成熟检测器阈值以及自体集自体半径、灰狼算法迭代次数等参数。

Step 2混沌初始化灰狼种群和设定算法参数a，A和C。

Step 3初始化前3 只狼的位置并计算每只灰狼个体的适应值。

Step 4记适应值最好的个体为Xα，适应值次之个体为Xβ，适应值再次之个体为Xδ。

Step 5在不与自体元素和已有成熟检测器发生免疫亲和的前提下结合莱维飞行策略搜索自体空间，通过公式（7）更新每个个体的位置。

Step 6更新灰狼算法参数a，A和C。

Step 7计算每只灰狼个体的适应值，并更新α，β，δ。

Step 8灰狼算法迭代次数加1，并判断算法迭代次数是否到达阈值。如果未到达、转到Step5。反之，继续执行算法。

Step 9得到Xα即为合格检测器的中心，α为合格检测器的半径。将合格检测器纳入成熟检测器集。

Step 10判断成熟检测器个数是否到达阈值要求，没有即转Step 2，达到要求则输出成熟检测器集并终止算法。

上文所述的算法保证了每次生成的成熟检测器尽可能拥有最大的半径以及最优的位置，但是由于迭代过程中迭代方向的不确定，使得落点在每次更换位置时要进行自体和检测器的免疫耐受，这使得在达到较高的覆盖率C1时迭代生成一个成熟检测器所需时间大大增加，延迟到达理想的覆盖率C2的时间。此时将优化算法的适应值由候选检测器半径改为检测器覆盖率，同时候选落点的亲和力计算只与自体元素进行。尽管这样会导致检测器重叠率增加，但是这样的重叠会更好地弥补检测黑洞的产生。

2.3 IGV-detector 算法收敛性分析

全局搜索算法的判敛准则及相关定义［15-16］如下。

定义1给定一个目标函数f，函数的解空间是从Rn到R，S是Rn的一个子集。在S中寻找一个点z，能够使得函数f的值最小化或者至少能够生成一个函数f在S上的可接受的下确界。

假设1f（H（z，ξ））≤f（z），如果ξ∈S，则f（H（z，ξ））≤f（ξ）。其中，H是指可以在待求解问题空间产生解的函数。假设1 要求H函数产生的新解优于当前解。z是存在于解的子集S中的某个最小值，ξ是根据相应算法在子集S中所得到的一系列的可行解。

定义2在Lebesgue 测度空间中，定义搜索的下界为：

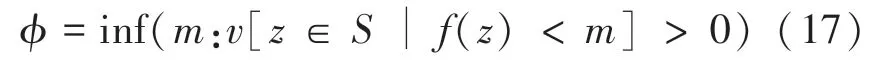
其中，v［A］是在集合A上的Lebesgue 测度。

引理1IGV-detector 算法满足假设1。

证明由于算法的迭代方向是单调的，即检测器的半径或者整体覆盖率都是逐渐变大的，所以本文算法明显满足假设1。

引理2IGV-detector 算法满足Condition 2。

证明假设2 是指对于位置测度为v的任意一个A的子集，如果采用随机抽样的方法，那么重复错过集合A的概率必定为零。由于算法的ε可接受区域Rε⊂S（Rε＝｛z∈S∣f（z）＜φ+ε｝，ε ＞0），所有在可接受区域取得点的概率肯定是非零值。文献［17］已经证明了原始灰狼算法的灰狼群状态空间的一般状态转移至最优状态的转移概率为1，即：

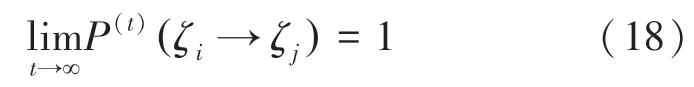
研究中证明了原始灰狼算法是全局收敛的，即满足上述条件。IGV-detector 算法是在GWO 算法的基础上运用混沌初始化和莱维飞行策略更新灰狼种群的位置。因此，对于原始灰狼算法种群，设其支撑集的并集为α；对运用混沌初始化以及莱维飞行作用的灰狼种群，设其支撑集的并集为β。由于2种改进策略的随机性，必然存在整数t1，使得当t ＞t1时，β⊇S。因此，对于IGV-detector 算法，存在整数t2，使得当t ＞t2时，α∪β⊇S。定义S的任意Borel 子集A＝Mi，t，则有v（A）＞0，μt［A］＝所以，IGVdetector 算法满足假设2。

定理2GWO 算法收敛到全局最优，即

证明由于IGV-detector 算法满足Condition 1和Condition 2，算法满足定理1 的条件，所以IGVdetector 算法是一个全局收敛算法，也即算法以概率1 全局收敛。

3 实验及结果分析

为了更直观地表示检测器分布情况，本文算法在二维数据集和公共数据集NSL-KDD 下进行了验证。实验在Matlab R2018b 软件下进行，其中主机配备16 GB 内存、Intel（R）Core（TM）i5-1035G1 CPU、Windows 10 操作系统。实验统计工具采用Matlab 自带的探查器工具。

3.1 算法在二维数据集下的验证

二维数据集选取的是Zhou［3］二维人造数据集。该数据集有环形及五角星等自体分布形态，每种形态有1 000 条自体数据，皆被归一化到［0，1］之间。本实验对比了V-detector 算法、粒子群优化［18］的PV-detector 算法、灰狼算法优化的GV-detector 算法以及改进灰狼算法优化的IGV-detector 算法，对比达到相同覆盖率所需检测器个数及时间、以及生成固定检测器个数所达到的覆盖率。

覆盖率的计算采取文献［3］中的方法，即在检测空间内随机采样m个点，如果有n个点未被覆盖到，则估计的覆盖范围为1-n／m。当期望的覆盖率为α＝1-n／m时，至少迭代的次数应为：

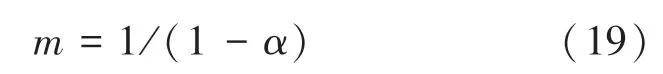
实验选取五角星二维空间和环形二维空间进行测试。设置PV-detector 算法、GV-detector 算法、IGV-detector 算法的寻优迭代次数为100，当本文算法生成检测器覆盖率在五角星二维空间下达到95%时，各算法生成检测器的分布覆盖情况如图3所示。

图3 4 种算法生成相同检测器的覆盖情况Fig.3 The coverage for the same detector generated by four algorithms

由图3 可知，由于V-detector 算法检测落点都是未加干预地随机产生，所以其重叠率较高，覆盖率较低；由于检测器的分布有了指导方向，所以其余3种算法的检测器分布更加合理，优先在目标空间边缘生成大半径检测器，有效避免了边缘检测黑洞的产生，覆盖率更高。同时由于粒子群算法陷入“早熟”现象，灰狼优化算法拥有比粒子群算法更好的寻优和避免陷入局部最优的能力［8］，所以GVdetector 算法、IGV-detector 算法的覆盖率比PVdetector 算法的覆盖率更高。同样地，由于引入了莱维飞行，使得算法在寻优过程中实现了对自体区域的跨越，覆盖效果更好。

为了验证改进算法的鲁棒性和稳定性，本文在相同条件下重复试验了20次，测试在五角星和环形二维数据集下进行，当达到相同覆盖率4 种算法所用时间和检测器个数详见表1、表2。

表1 达到95%覆盖率所用时间对比Tab.1 Comparison of the time to reach 95%coverage

表2 达到95%覆盖率所用检测器个数对比Tab.2 Comparison of the number of detectors to achieve 95%coverage

3.2 算法在公共数据集下的验证

公共数据集采取NSL-KDD 数据集，该数据集是KDD CUP99 数据集的改进版本，相较于后者，NSL-KDD 去除了大量的冗余信息，训练集和测试集的数据规模缩小后使数据集变得更加合理，同时使得实验有了一致性和可对比性。NSL-KDD 里面训练集包含125 973 条记录，测试集包含22 544 条记录，其中数据维数为42 维。本文实验选取了其中20%的数据。

在数据预处理部分，由于原始数据的离散性，需要进行连续化处理。比如协议类型部分，变换规则为：TCP →1；UDP →2；ICMP →3 等。同时由于高维数据对检测率的影响［19］，需要对数据进行降维处理。数据的降维方式有很多，本文选取的是比较成熟的PCA 方法，选择保留90%的特征降维后数据维度为20 维。自体集数据的半径对最终的实验检测指标的影响是巨大的，本文的自体集数据半径设为0.01。归一化方法选择最大最小归一化方法，方法公式具体如下：

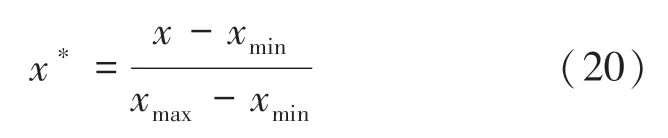
其中，xmin为样本中数据最小值，xmax为样本中数据最大值。

入侵检测对应于实际应用的评价指标主要有检测率、误报率等，本实验测试了4 种算法不同的检测器数量对应的检测率。结果如图4 所示。由图4 中分析可知，V-detector 由于其生成检测器分布的不确定性，检测率呈现缓慢递增的趋势。其余3 种优化算法在检测器数目较少时便能达到较理想的检测率，这是因为在检测器生成早期优先生成高质量的检测器，在算法后期生成的检测器多用于弥补检测黑洞，因此检测率增长缓慢，但总地来看优化后的算法仍能以相对较少的检测器数量达到较高的检测率。

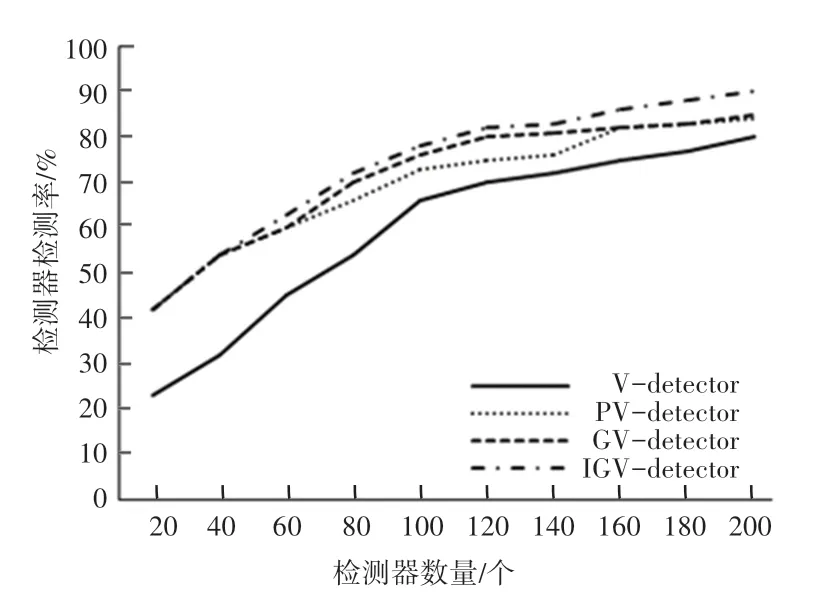
图4 4 种算法生成相同检测器数量与检测率关系Fig.4 The relationship between the number of detectors and the detection rate generated by the four algorithms

生成200 个检测器所需时间对比见表3。由表3 可知，达到相同检测率优化后的算法所需时间更短。

表3 生成200 个检测器所需时间对比Tab.3 Comparison of the time required to generate 200 detectors

总地来看，IGV-detector 算法能在较短的时间达到更高的检测率，符合入侵检测实时性的要求。

4 结束语

本文通过引入灰狼优化算法对经典算法Vdetector 检测器的分布进行了优化。灰狼优化算法等元启发式方法由于其无需计算导数、无需过多先验知识等优点在近些年受到了大量关注。Vdetector 继承了否定选择算法的“基因”，即检测器都是随机产生的。在自体空间未知的情况下，随机似乎更能满足检测器分布广泛的需求。在引入灰狼优化算法之后，检测器的耐受分布便有了指导的方向，同时由于群体寻优的机制存在可以更好地应对复杂的自体空间。结果表明，改进后的V-detector算法提高了检测器的质量，减少了不必要的检测器重叠以及对检测黑洞进行了更好的覆盖。但是由于迭代过程中寻优方向的不确定性，导致每次产生的新的候选落点都要与自体和已有成熟检测器进行免疫耐受，这种不确定性导致了在检测器生成后期生成一个成熟检测器的时间有所增加。以后的改进方向应是对迭代落点的方向进行引导，避免或者减少这种大量的亲和力计算。