基于稀疏化训练和聚类降低IR-Drop 影响的方法

王子杰

（合肥工业大学 计算机与信息学院，合肥 230601）

0 引言

目前，卷积神经网络已经广泛应用于深度学习中。研究表明，在卷积神经网络中乘法和累加运算占整个操作的90%以上［1］。但随着神经网络不断加深，利用传统CMOS 器件组成的神经网络由于存在着计算时间过长和能耗过大的问题［2］，规模已经很难增大。新型器件忆阻器为实现矩阵乘法提供了一种更高效的方式［3］，能够以O（1）的时间复杂度实现矩阵乘法，且具有极低的能耗［4］。基于忆阻器［5-7］构建的神经网络［8］可以加速神经网络的计算，加快神经网络对于大规模数据的处理速度。

通过忆阻器阵列［9］加速神经网络计算，首先需要在软件上训练神经网络得到权值矩阵，然后通过施加电压改变忆阻器的阻值将权值矩阵映射为忆阻器电导矩阵。但由于IR-Drop 的存在，在运算的过程中，实际施加在忆阻器上的电压和预期的电压不同，计算结果和理想中预期的结果存在偏差，造成计算精度低的情况出现。

在忆阻器阵列中距输入端越远的忆阻器受到IR-Drop 的影响越大，因为随着导线长度增加、导线电阻也会变大，而距施加电压的输入端越近的忆阻器受到的影响越小，所以忆阻器阵列规模越大，受到的IR-Drop 影响就越大。随着神经网络的规模增加，相应的忆阻器阵列规模增大，计算精度也会下降。例如当忆阻器阵列规模从16×16 增大到128×128时，在IR-Drop 的影响下，忆阻器阵列的计算精度降低了35%［10］。为了解决这一问题，在硬件和软件方面上，研究人员都提出了一些有效的解决方案。

硬件方面，Huang 等人［11］提出补偿输出电流的方法来提高计算精度。该方法首先求出在理想情况下忆阻器阵列中每一列输出的电流大小，然后在忆阻器阵列中新增行，对新增行施加电压来补偿电流输出，使得每一列的输出电流达到理想的电流大小。但是这种方式会增加过多的硬件开销。为了减少硬件开销，Zhu 等人［12］提出了一种新的补偿电流的方法来提高计算精度。该方法在忆阻器阵列每一列的输出端新增读出放大器（sense amplififier），并对每一列的输出电流调整放大的倍数使得电流输出达到理想的电流大小。文献［11-12］中的方法都会额外增加硬件的开销，而软件的解决方式则不会额外增加硬件开销。

在软件方面，主要是采取缩减忆阻器阵列规模来降低IR-Drop 的影响，忆阻器阵列规模越小，受到的IR-Drop 影响就越小，计算精度就越高。Wang 等人［13］提出通过PCA 分解矩阵的方式来提高计算精度。通过将一个大的忆阻器阵列分解成若干个小的忆阻器阵列的方式来减少忆阻器阵列规模［14］。但分解过后的忆阻器阵列计算精度较低，所以需要对神经网络进行重新训练来提高计算精度。而Liu 等人［10］提出通过SVD 分解矩阵的方式［15］来提高计算精度，这种方式不需要对神经网络进行重新训练，相对于PCA 分解矩阵的方式计算精度较高。文献［10，14］中采用分解矩阵的方法得到的忆阻器阵列规模较大，仍然会受到较大的IR-Drop 影响，忆阻器阵列的计算精度较低。

为了解决IR-Drop 对计算精度的影响，本文提出基于对权值矩阵稀疏化以及对权值矩阵的行向量进行聚类的方案（Sparse Training Clustering，STC）来提高计算精度，为了描述方便，本文余下部分对所提方案简称STC 方案。首先，对神经网络进行稀疏化训练，将神经网络的权值矩阵上行号、列号之和较大的权值置零且保证计算精度大于阈值p。然后对矩阵的行向量进行聚类，将全零行向量和近似全零行向量聚集在一起，将其权值置零并且在保证零权值不变和神经网络的计算精度大于阈值γ 的前提下重新训练神经网络得到新的权值矩阵，接着删除权值矩阵的全零行向量和全零列向量减少矩阵规模。最后在IR-Drop 下计算行向量的权值损失，将行向量按照损失大小降序排列得到新的权值矩阵并且映射到忆阻器阵列上。STC 方案可以有效地降低忆阻器阵列的规模，同时仍然保持较高的计算精度。

1 忆阻器阵列

利用忆阻器阵列实现矩阵乘法，首先需要将训练好的神经网络的权值矩阵Wn×m映射到忆阻器阵列上，忆阻器阵列如图1 所示。用忆阻器阵列上的忆阻器电导值gij来代表权值矩阵上的权值wij，对每一行施加电压V＝｛V1，V2，…，Vn｝，第j列的输出电流的计算公式可表示为：

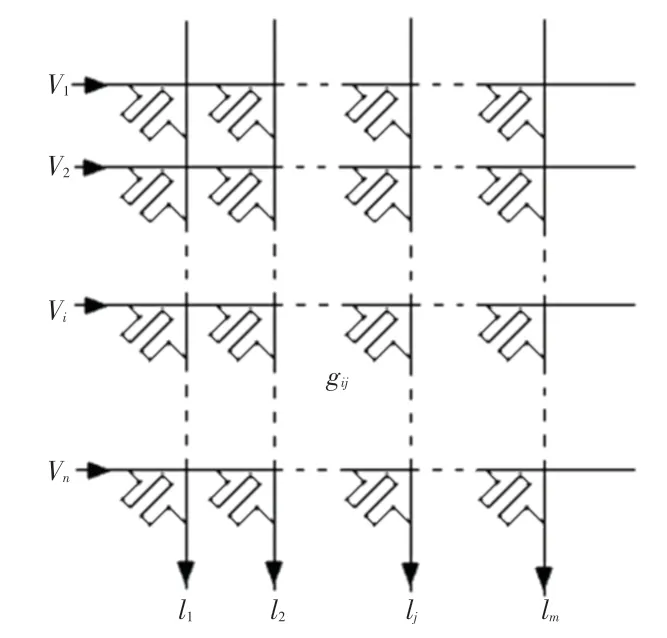
图1 忆阻器阵列Fig.1 Memristor based Crossbar

其中，Vi为第i行的输入，Ij为第j列输出。因为施加电压在电阻上可以得到一个电流，并且在导线上输出端会输出电流之和，这个速度比起传统的计算要快，所以忆阻器阵列可以加速神经网络的计算速度。为了描述方便，本文余下部分对于忆阻器阵列上的电导值统称为忆阻器阵列的权值。

2 STC 方案流程

STC 方案的流程图如图2 所示。STC 方案首先需要输入模拟忆阻器阵列上IR-Drop 影响的矩阵In×m和神经网络的权值矩阵Sn×m，In×m·Sn×m代表In×m和Sn×m对应位置相乘得到的矩阵。用神经网络的权值矩阵In×m·Sn×m的计算精度来代表在IRDrop 下矩阵Sn×m映射到忆阻器阵列上的计算精度。然后稀疏化训练将Sn×m上行号、列号之和较大的权值置零，因为行号、列号之和较大的权值在忆阻器阵列上距离输入端较远，受到的IR-Drop 影响较大。紧接着得到在IR-Drop 影响下计算精度高于阈值p的神经网络权值矩阵Cn×m。接下来，对Cn×m的行向量进行聚类，将全零行向量和近似全零行向量聚集在一组，将近似全零行向量的权值置零、并且在保证零权值不变的前提下重新训练神经网络得到计算精度高于阈值γ的神经网络权值矩阵Dn×m。同时，删除矩阵Dn×m的全零行向量和全零列向量得到矩阵Kl×h。最后，在IR-Drop 影响下计算矩阵Kl×h行向量的权值损失，将行向量按照损失大小降序排列得到新的权值矩阵Fl×h，并将权值矩阵Fl×h映射到忆阻器阵列上。对STC 方案流程，本文拟展开研究分述如下。

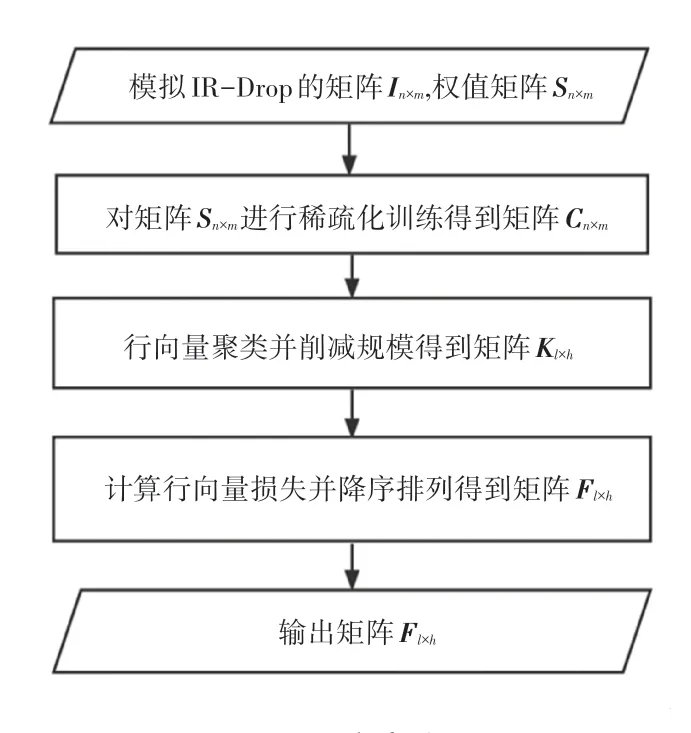
图2 STC 方案流程图Fig.2 Flow chart of STC scheme

2.1 稀疏化训练

IR-Drop 影响大小是由忆阻器阻值以及导线电阻决定的［10］，随着忆阻器规模的增大，导线电阻增加，IR-Drop 影响也会增加。如果忆阻器的电阻设置为最大、即权值为零，此时导线电阻分压的影响就会降低，IR-Drop 影响就会降低，计算精度也随之提高。在STC 方案中，经过稀疏化训练的权值矩阵有大量的零权值，映射在忆阻器阵列上受到的IRDrop 影响较小，计算精度显著提升。关于稀疏化的训练过程，其代码表述具体如下。

输入权值矩阵Sn×m，模拟忆阻器阵列上IR -Drop 影响的矩阵In×m，阈值q，阈值p

输出稀疏化后的矩阵Cn×m

综上可知，输入为神经网络的权值矩阵Sn×m，模拟忆阻器阵列上IR-Drop 影响的矩阵In×m，阈值q和p。第1 行给阈值q和p赋值，权值的行号、列号之和超过q代表在忆阻器阵列上此权值与输入端相距较远，受到的IR-Drop 影响较大，p为神经网络计算精度阈值。第2行将Sn×m赋值给Cn×m，第3行In×m·Cn×m代表In×m和Cn×m对应位置相乘得到的矩阵，神经网络的权值矩阵In×m·Cn×m的计算精度代表在IR-Drop 下矩阵Sn×m映射到忆阻器阵列上的计算精度，计算精度超过p则停止训练。第4 行重新将Sn×m赋值给Cn×m用于稀疏化训练。第5～10 行当矩阵Cn× m上的权值行号、列号之和大于q时置零，第11 行在保证零权值不变的情况下重新训练神经网络。第12 行缩小稀疏化范围，因为神经网络的计算精度还未超过p，通过改变稀疏化范围使得神经网络计算精度超过p。第14行输出计算精度高于p的神经网络权值矩阵Cn×m。

2.2 聚类并削减矩阵规模

经过了神经网络的稀疏化训练后，STC 方案对矩阵Cn×m上的行向量进行聚类，找到全零行向量和近似全零行向量的集合。首先定义一个阈值γ，在神经网络的计算精度高于γ 的前提下，将权值矩阵的近似全零行向量的权值置零，然后保证零权值不变并重新训练神经网络，使得权值矩阵有更多的全零行向量，最后删除矩阵的全零行向量和全零列向量，降低权值矩阵的规模。对聚类并削减矩阵规模过程，可给出设计描述如下。

输入稀疏化后的矩阵Cn×m，忆阻器阵列IRDrop 分布信息矩阵In×m，半径h，阈值γ

输出经过删减的新矩阵Kl×h

综上可知，输入为经过稀疏化的矩阵Cn×m，模拟忆阻器阵列上IR-Drop 影响的矩阵In×m，半径h，阈值γ。第1 行给h和γ赋值，若行向量与全零行向量距离h以内的则为近似全零行向量，γ为神经网络计算精度阈值。例如：

第2 行是将矩阵Cn×m赋值给Rown×m。第3 行的In×m·Rown×m为In×m和Rown×m对应位置相乘得到的矩阵，神经网络的权值矩阵In×m·Rown×m的计算精度代表在IR -Drop 下矩阵Rown×m映射到忆阻器阵列上的计算精度，当计算精度超过γ时停止训练。第4 行重新将Cn×m赋值给Rown×m，第5 行对Row采用mean-shift 算法聚类并得到result分类集合。mean -shift 算法的聚类中心处于最高密度处，由于矩阵Cn×m经过稀疏化训练，所以全零行向量这一类型必定最多，所以得到的聚类中心相对来说比较准确。mean -shift 算法中的h表示如果2 个向量距离h以内则为同一类，将h设为0.1 可得：

第6～16 行寻找result内拥有全零行向量和近似全零行向量的集合，并将集合编号赋值给flag，再将result编号为flag的集合内所有行向量权值置零，result［i］代表第i个集合，result［i］［j］代表第i个集合的第j个行向量。第17～18 行将result赋值给Rown×m，同时保证零权值不变的前提下重新训练神经网络。第19 行减少h，因为神经网络计算精度还没超过γ，h越小、近似全零行向量越少，则进行重训练后的神经网络计算精度越高，不断改变h的大小，直到神经网络的计算精度超过γ。第21 行得到计算精度高于γ的神经网络权值矩阵Rown×m，并将其赋值给矩阵Dn×m，推导后得到的运算结果如下：

在22～29 行删除矩阵Dn×m的全零行向量和全零列向量得到新矩阵Kl×h并输出，并可表示为：

2.3 行向量排序

对于删减后的权值矩阵Kl×h，STC 方案通过对其行向量采用排序的方式来提高计算精度。采用如下步骤：

（1）设定一个向量b，利用b来代表IR-Drop 的影响下权值矩阵上行向量的每个权值损失比例。

（2）利用b计算权值矩阵行向量的权值损失大小，将行向量按照损失大小降序排列得到新的矩阵。

这样将容易受到IR-Drop 影响的行向量放到在忆阻器阵列上受IR-Drop 影响小的位置，而将不易受到IR-Drop 影响的行向量放到在忆阻器阵列上受IR-Drop 影响大的位置上，使得整体受到的IR-Drop影响降低。行向量排序过程可做完整描述如下。

输入经过删减的矩阵Kl×h，向量b

输出经过排序的新矩阵Fl×h

分析可知，输入为经过删减的矩阵Kl×h和向量b。例如：

第1～3行，用b计算矩阵Kl×h的行向量的权值损失，并且和行向量建立匹配关系map，对map的行向量的权值损失进行降序排序。K［i］为矩阵Kl×h的第i个行向量，K［i］·b为第i个行向量和向量b的内积结果，map.first存放行向量的权值损失，map.second存放对应的行向量。为此，可以得到：

第4～5行，将map上的行向量赋值给矩阵Fl×h并输出，求得的结果可写为：

3 实验结果以及分析

3.1 实验参数设置

本实验在Pytorch 上构建了一个3 层卷积神经网络，采用MINST 数据集对其进行仿真测试。卷积神经网络主要包括2 个卷积层、2 个池化层和1 个全连接层。输入图像的大小为28×28。忆阻器的电阻范围为10 kΩ～1 MΩ，忆阻器阵列中忆阻单元之间的导线电阻为2.5 Ω，忆阻器阵列规模分别为64×64、96×96 和128×128，参数配置见表1。在IRDrop 的影响下，施加到忆阻器两端的电压受到忆阻器处于忆阻器阵列的位置的影响，根据文献［10］中的忆阻器阵列的实际退化情况得到模拟结果，按照模拟结果来表示IR-Drop 的影响。

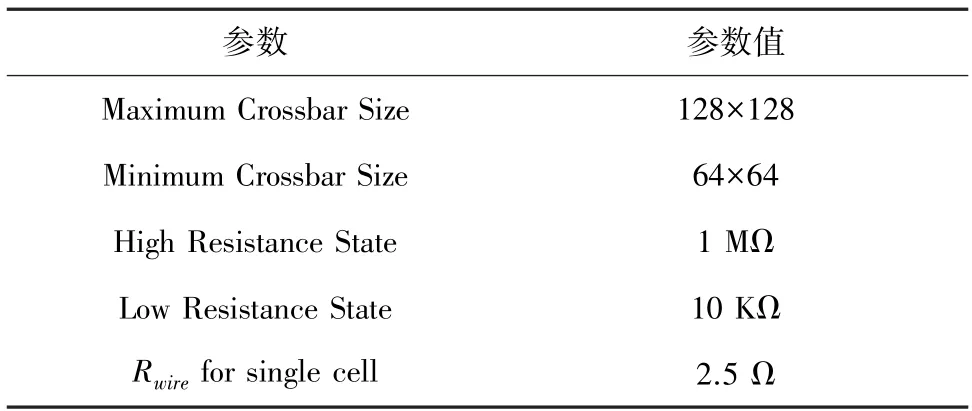
表1 实验参数设置Tab.1 Experimental parameters setting

3.2 实验结果分析

本实验将STC 方案和SVD 方案在不同规模的忆阻器阵列上的计算精度和硬件规模开销上做了对比。STC 方案和SVD 方案在计算精度的对比如图3所示，图3 展示了不同规模的忆阻器阵列在4 种情况下的计算精度，分别是权值矩阵在有IR-Drop 影响下和无IR-Drop 影响下的计算精度，采用SVD 方案和STC 方案的计算精度。在IR-Drop 的影响下，随着忆阻器阵列规模的增加，计算精度会不断下降，STC 方案和SVD 方案有效地提升了在IR-Drop 影响下忆阻器阵列的计算精度，并且STC 方案与SVD方案相比计算精度较高。这主要是因为采用STC方案得到的矩阵有大量零权值，零权值受到IRDrop 的影响很小，所以忆阻器整体受到的IR-Drop影响较小。而SVD 方案得到的矩阵规模较大，所以仍然会受到较大的IR-Drop 影响。可以看出STC方案在忆阻器规模较小的时候计算精度的提升较小，而对于较大规模的忆阻器阵列计算精度提升较大。

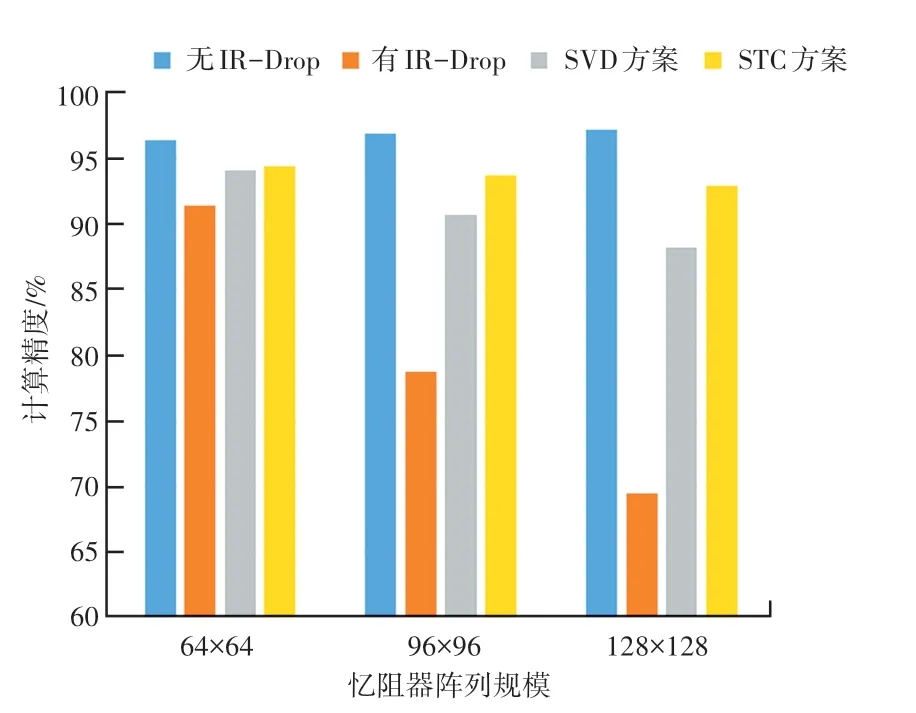
图3 不同规模的忆阻器阵列的计算精度Fig.3 Calculation accuracy of Memristor based Crossbar of different sizes

STC 方案和SVD 方案在硬件规模开销对比见表2。表2 展示了不同规模的忆阻器阵列，采用STC 方案和SVD 方案所使用硬件规模的比较。SVD 方案会把矩阵分解成2 个小矩阵，STC 方案则直接将一个大矩阵缩减成小矩阵。STC 方案在硬件规模的缩减大小上比SVD 方案要高。这主要是因为STC 方案采用稀疏化训练的方式使得零权值大量分布于神经网络的权值矩阵上，因此权值矩阵上可以删除许多全零行向量和全零列向量来减少矩阵规模，而SVD 方案为了提高计算精度，得到的矩阵规模较大。STC 方案对于较大规模忆阻器阵列的硬件规模削减效果更好，例如对于128×128 大小的忆阻器阵列缩减了77.29%，而对于64×64 大小的忆阻器阵列只减少了23.44%。

表2 不同规模的忆阻器阵列的硬件规模Tab.2 Hardware scale of Memristor based Crossbar of different sizes

在STC 方案中，通过调整稀疏化范围来得到不同规模的忆阻器阵列的计算精度和硬件规模的开销，针对不同规模的忆阻器阵列的计算精度如图4所示。图4中，横坐标表示忆阻器阵列上的权值的行号、列号之和大于该值则需要置零。随着神经网络稀疏化范围的减小，忆阻器阵列的计算精度提高。因为在40～60 的范围内，忆阻器阵列上的大权值受到的IR-Drop 影响较小。随着权值矩阵稀疏化训练范围的减小，在神经网络训练的过程中可以进行调整的权值数量增加，神经网络的计算精度就会提高，权值矩阵映射到忆阻器阵列上的计算精度也会增加。因此在一定范围内减少神经网络稀疏化训练的范围可以提高忆阻器阵列的计算精度，但是如果神经网络稀疏化范围太小，忆阻器阵列就会受到较大的IR-Drop 的影响，计算精度反而会下降。

针对不同规模的忆阻器阵列缩减后的硬件规模如图5 所示。图5中，横坐标表示忆阻器阵列上的权值行号、列号之和大于该值则需要置零。随着神经网络稀疏化范围的减小，硬件规模的大小增加。因为随着稀疏化范围的减小，权值矩阵上全零行向量和全零列向量的数量就会变少，权值矩阵的规模增加，所以映射到忆阻器阵列上后的硬件开销就会增加。

从图4 和图5 可以看出，通过设置不同的稀疏化范围会导致不同的计算精度和硬件规模的开销，这里STC 方案以最高计算精度为选取方案。

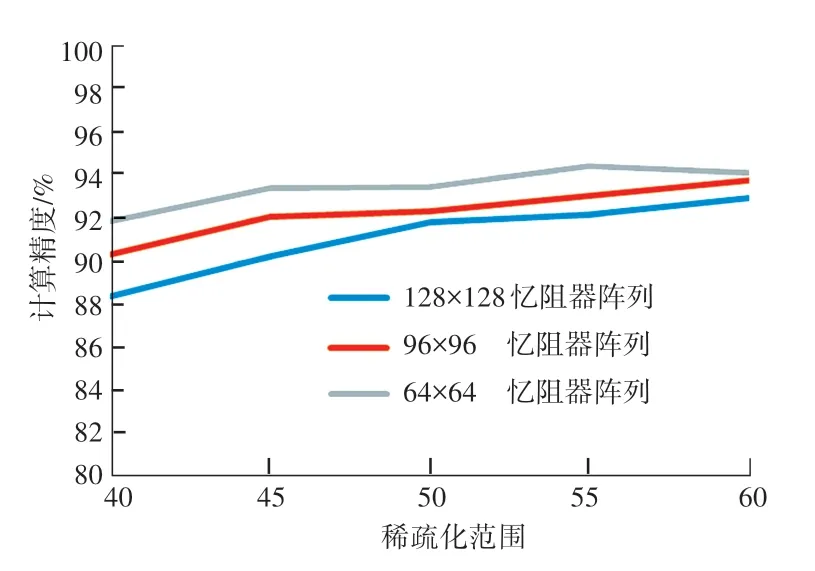
图4 不同规模的忆阻器阵列计算精度Fig.4 Calculation accuracy of Memristor based Crossbar of different sizes

图5 不同规模的忆阻器阵列硬件规模Fig.5 Hardware scale of Memristor based Crossbar with different sizes

4 结束语

忆阻器阵列在神经网络计算加速上有着很好的效果，但是会受到IR-Drop 的影响，从而造成计算精度的下降。本文提出了STC 方案用于降低IR-Drop的影响，提高计算精度。该方案基于对权值矩阵进行稀疏化以及对权值矩阵的行向量进行聚类来实现，可以有效提高计算精度，并且减少了硬件规模的开销。根据实验结果表明，经过STC 方案处理的忆阻器阵列在IR-Drop 的影响下，计算精度显著提高，硬件规模大大降低。