耦合深度学习-运动学的自动驾驶一体化换道研究

熊明强，谯 杰，王 亮，夏 芹，江 萌

（1.中国汽车工程研究院股份有限公司，重庆 401122；2.汽车噪声振动和安全技术国家重点实验室，重庆 401122；3.中国城市规划设计研究院西部分院，重庆 401122）

近年来，自动驾驶技术引起了世界各国的广泛关注［1-10］，被认为是缓解交通拥堵，减少交通事故和环境污染的重要技术［1，6，11］。目前一些自动驾驶已经进行了大规模的道路测试，比如谷歌自动驾驶和苹果自动驾驶。研究表明［12］，在如今的交通事故中，有超过30%的道路交通事故是由不合理的换道行为引起的。

目前基于机器学习的方法对自动换道轨迹进行的研究还比较少［13-15］，利用机器学习进行自动驾驶车辆换道轨迹规划的模型需要经过大量已有的换道数据训练来确定。YAO Wen等［13］将k最近邻算法应用到换道轨迹规划中，但是该模型所用到的数据较为有限且覆盖场景不足。在此基础上，DING Chenxi等［14］构建了两层BP神经网络对NGSIM数据［16］进行学习，从而对车辆换道进行端到端的轨迹预测，但是k最近邻算法和BP神经网络对于换道这类时间序列数据处理能力有限，通常是单一地复制已有的数据，并未对数据前后帧的内部逻辑进行判断和处理［17］。XIE Dongfan等［15］利用经典LSTM神经网络预测自动驾驶车辆换道轨迹，该模型对换道轨迹曲线的学习结果取得了较高的精度，但是没有对训练过程中的一些不安全因素进行限制。考虑到现有基于深度学习的自动驾驶车辆换道轨迹规划算法只是单一地复制已有的换道轨迹，忽略了换道过程中的动态变化，这样的模型对于换道条件过于苛刻，无法用于现实环境。反观人类在对于新事物的学习过程中，一方面由已有的理论经验对新事物的反应进行指导，另一方面，面对新事物时，人类也在不断的实践过程中形成自己的经验。本文借鉴了人类对于新事物的学习过程，将所训练的BP神经网络进行嵌套，从而建立一种可嵌入的深度学习网络模型，该模型有效地继承了以往数据的换道行为特征，同时能缩短对新数据的学习过程。

1 嵌入神经网络换道模型

随着近年神经网络的不断发展，各种被用于不同领域的神经网络被不断地提出和优化，但无论是哪种神经网络，其方法大致上都在模仿人的学习过程。人在最初对一个事物进行学习时，实际上是从两个方面来进行学习的，一个方面是对该事物已经形成的知识进行学习，另一个方面是通过不断的实践进行学习，借鉴这种思路，本文提出了一种新的神经网络模型，该神经网络模型旨在更加具体地模仿人的学习过程，如图1所示。

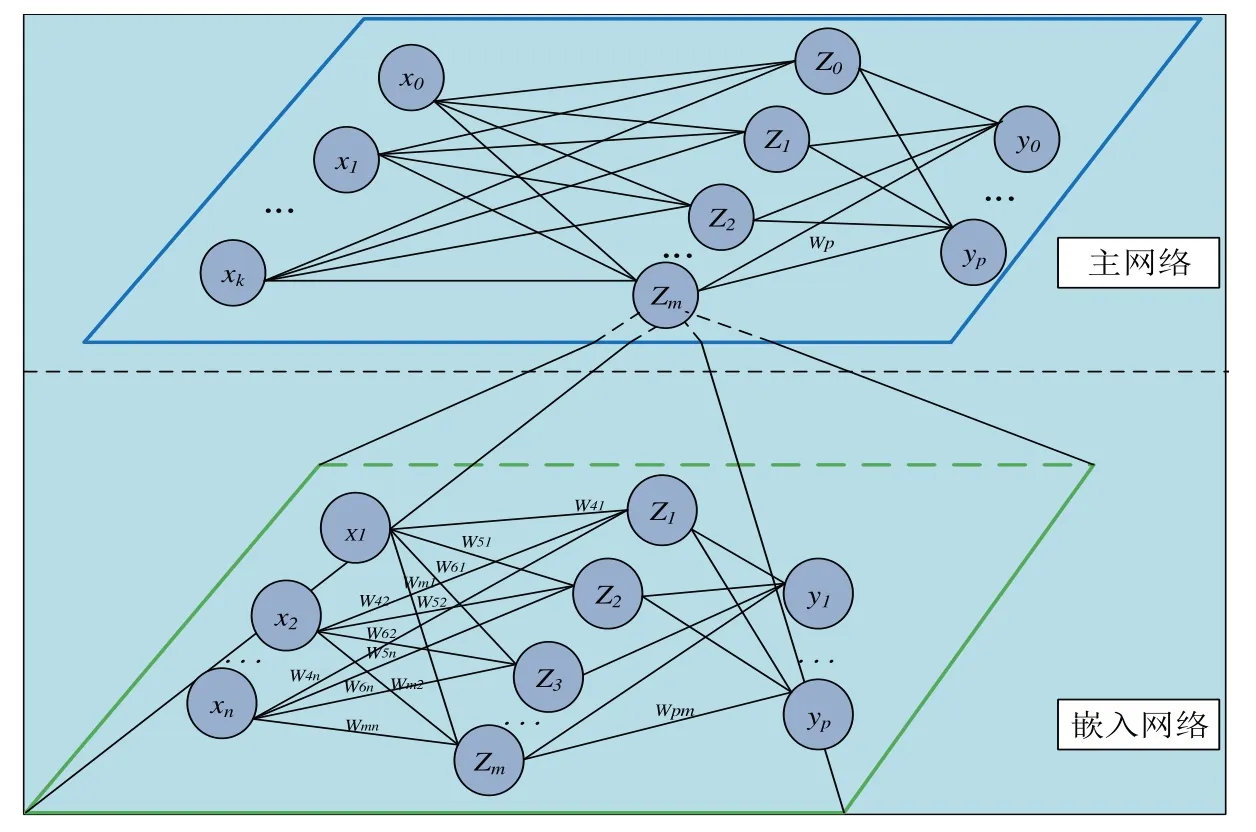
图1 神经网络嵌入过程

该神经网络模型有两级，第1级横向上是一个3层的全连接网络，第2层是嵌入层，嵌入层里面每一个神经元都是一个单独的神经网络，第2级是需要嵌入的神经网络。本文把这些嵌套的神经网络暂定为BP神经网络，这些BP神经网络分为两种：（1）根据需要已经训练好；（2）尚未进行训练。由此实现在学习过程中既能够学到已有的知识，又能通过尚未训练的神经网络进行学习的目的。所以神经网络参数分为横向参数和纵向参数。

1.1 横向参数

一般而言，本文设计的神经网络主要由以下3个部分组成：输入层、嵌入层和输出层。

输入层：根据不同学习对象的实际情况，设定神经元数量。输入的数据为交通环境数据，即上一时刻换道车辆和换道车辆周边车辆的位置、速度、加速度等数据。

嵌入层：由于嵌入层内部各个神经元可能用到的输入变量长度不一样，所以本文设置了嵌入层，嵌入层神经元的数量根据实际情况进行寻优及测试。

输出层：根据实际问题需要设置数量，输出为神经网络预测的下一时刻换道车辆位置和速度。

1.2 纵向参数

纵向上，各层神经元由两部分构成，一部分是已经训练好的神经网络（图1主神经网络），以激活函数的形式嵌入，但这些神经网络必须针对同样的问题，利用不同数据进行训练后得到的，这些神经网络在训练的过程中不需要进行参数调整，只需要利用输入，得到输出结果即可。如有需要，可嵌入没有训练过的神经网络，在主神经网络训练的过程中进行同步训练。

1.3 数学模型

耦合的表现形式为两个或两个以上的系统构成一个网络时，若其中某一子系统中数据发生变化，能影响到其他子系统数据也发生类似的变化。其机理也多种多样，本节主要采取数据耦合的方式。基于深度学习的方式无法规避换道过程中的危险因素，单一地复刻已有数据，且是黑盒模式导致无法控制训练参数。基于规则的模型都是对显性数据进行计算，无法研究交通环境中隐形数据对换道过程的影响。本文将二者结合起来，试图寻找通过一种机制让二者互补的方式，如图2所示。

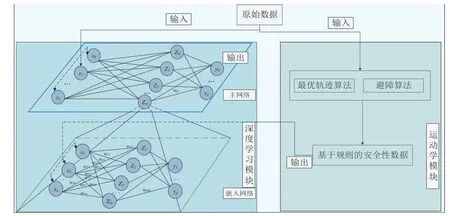
图2 神经网络和规则的耦合过程

深度学习模块的训练是持续的，深度学习模块在训练的过程中，运动学模块不断地向深度学习模块传递安全性的数据，让深度学习也不断对安全性数据进行学习，虽然无法控制训练过程中的参数，但是这种数据耦合的方式可以在训练中潜移默化地让模型更具安全性。

机器学习的过程，就是通过数据的前向传播求得预测值和真实值的误差，用反向传播算法缩小误差的一个过程。在进行前向传播之前，本文会根据特定的问题和基于规则的换道数据和基于人类的换道数据训练若干个BP神经网络net1，net2，…netn，本文将这些神经网络以替换的方式，将经典的BP神经网络中的激活函数替换，原激活函数的输入变为嵌入神经元的输入，原激活函数的输出变为嵌入神经元的输出。

1.3.1 前向传播

如果一个经典BP神经网络有若干个输出神经元，该网络每一次前向传播后，任意一个神经元j的输入是：

第j个神经元的输出是：

式中：f（）是激活函数，在本方法中激活函数为：

式中：net为嵌入的BP经网络。

本文令隐藏层任意神经元h的输入为：

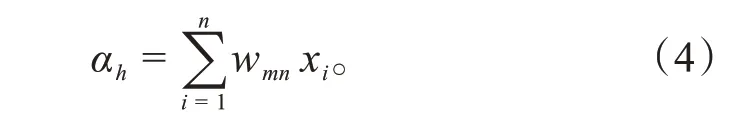
式中：wmn是隐藏层与输入层的连接权重。

令输出层任意神经元j的输出为：

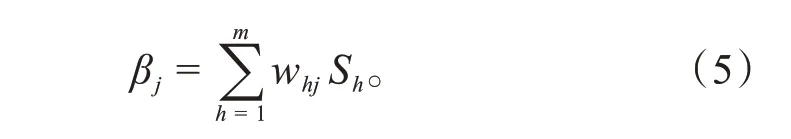
式中：Sh为隐层神经元h的输出。

式中：f（）为激活函数。

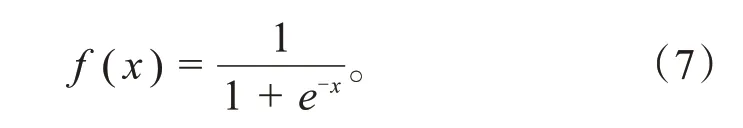
最终得到嵌入神经网络的p个输出=即：

所以主神经网络神经元j的输入值为：

主神经网络与真实值相比误差为：

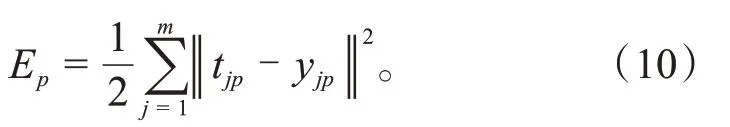
1.3.2 反向传播

至此，一次前向传播结束，神经网络的最终目标是要使误差尽可能地小，所以需要将前向传播所得到的误差进行反向传播，训练得到相应的参数w，设第一层神经网络权值矩阵为Wl=嵌入神经网络权重矩阵为Wq=嵌入层神经网络参数调整方式为：

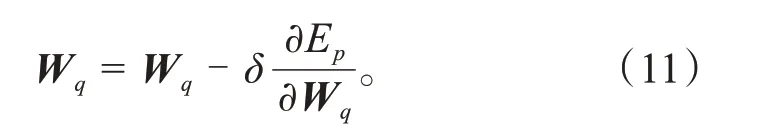
输出层第j个神经元所对应的误差为：

以图1中权重矩阵Wpm为例进行说明：

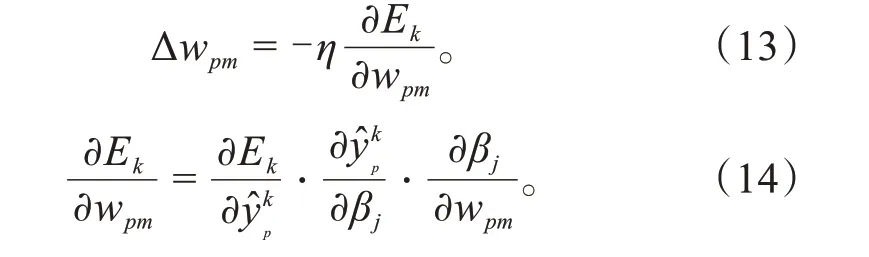
根据βj的定义，显然有：

将式（14）和式（15）代入式（13），得到Wpm的更新公式为：

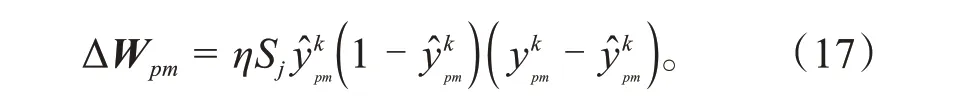
式中：学习率η∈(0，1)。

将式（12）具体化为：

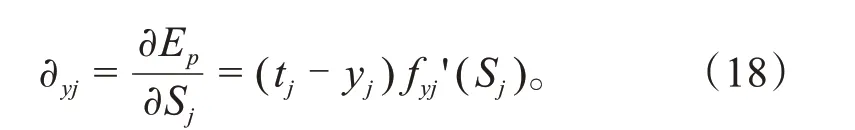
式中：fyj'(Sj)为输出层第j个神经元对应的Sj的传播方程导数，得到损失矩阵为：

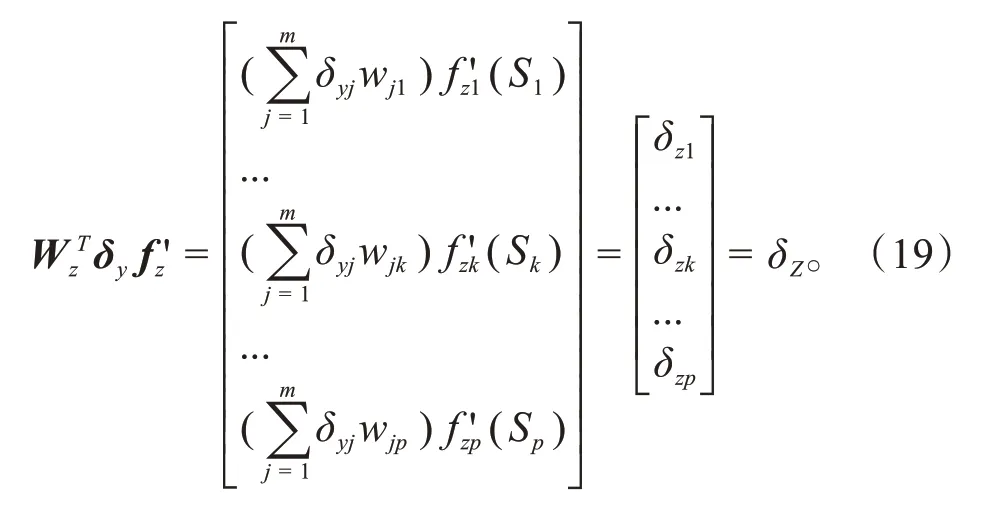
主神经网络权重的更新方式为：

1.3.3 最优轨迹模型

自动驾驶车辆在换道过程中，会根据实时交通环境进行轨迹规划，每个时间步长内会为车辆规划出最优的换道轨迹，由于基于时间多项式的换道轨迹算法计算较为复杂，可能存在较大延迟，本文选择形式较为简单的3次多项式作为基于规则的轨迹规划算法，其表达式为：

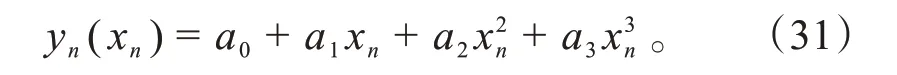
式中：a0、a1、a2、a3均为待确定的参数；xn为车辆n的纵向位置；yn为车辆n的横向位置。确定各项参数有：

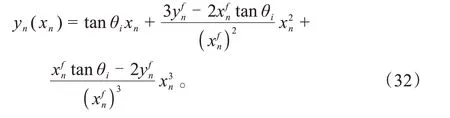
式中：θi为规划步长起点的航向角；为终点横向坐标，均为已知量。

1.3.4 避障算法

在图3中，换道车辆为主车辆SV，当前车道前车为PV，以及目标车道前车LV和目标车道后车FV。其中，穿过车道变化的虚线是车辆SV的换道轨迹，包括换道准备OP和换道执行PD两个阶段，车辆SV在O点开始换道准备，在P点完成换道准备开始换道执行，在D点完成换道。若定义换道执行开始点为坐标原点，那么换道执行开始点P的位置坐标为（0，0），换道执行结束点的坐标为（xf，yf）。车辆SV在换道准备过程中受到PV的影响，当换道条件满足的时候进行换道执行，车辆从当前车道中心线移动到目标车辆中心线，根据Gipps模型［18］的推演，在执行换道过程中受到车辆LV和FV的影响，车辆SV在换道过程中主要受这3辆车的影响。车辆在换道过程中，可能的冲突区域如图3所示.

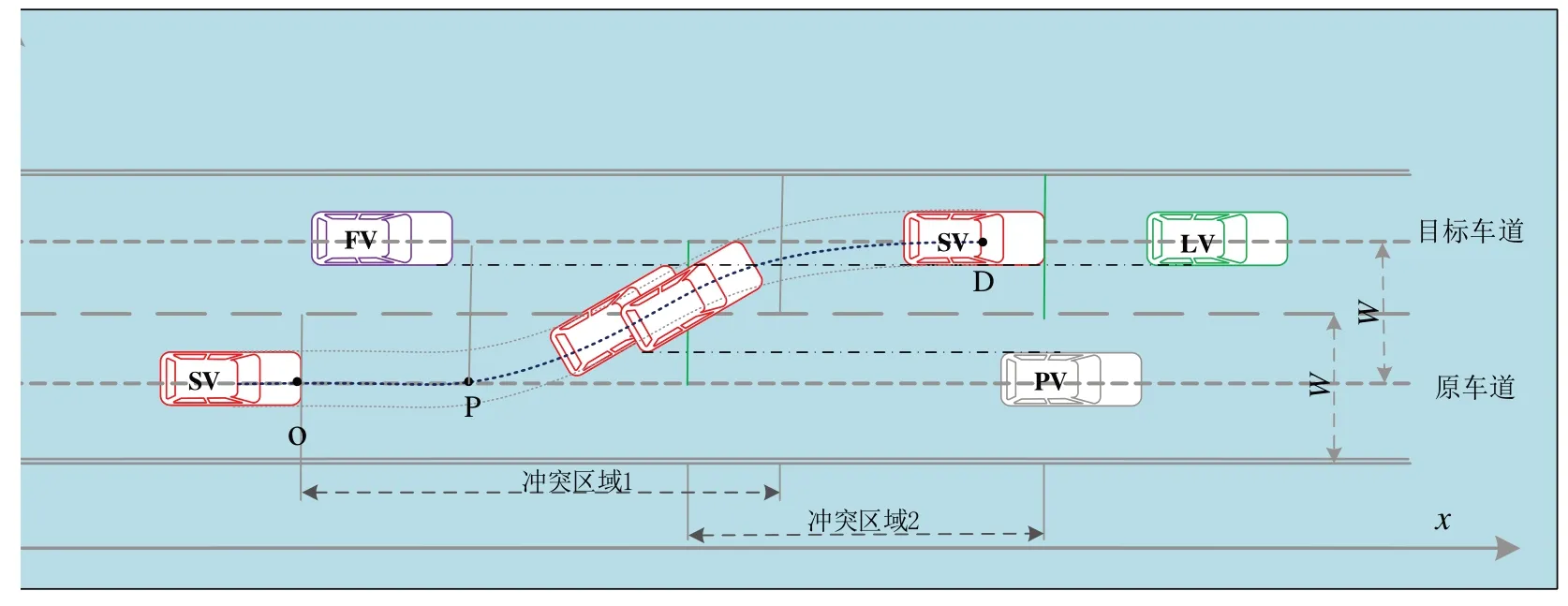
图3 冲突区域

Gipps模型是领域内经典的车辆安全距离模型，可以较好地拟合两辆跟驰车辆之间的行驶状态，但没有考虑车辆车身长度。所以本文在经典Gipps模型的基础上加入车身长度进行改进，作为3次轨迹曲线的约束条件。

车辆换道过程中受到周围车辆实时的影响，为了保证换道过程的安全性，需要实时检测周围车辆的行驶状态，并对周围车辆的行驶状态进行预测。

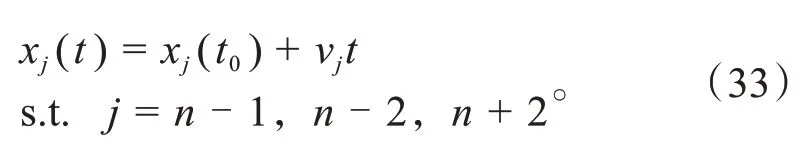
式中：j为编号为n-1的车辆；xj（t0）为t0时刻车辆j的纵向位置；vj为车辆j的速度；xj（t）为t时刻车辆j的纵向位置。

Gipps模型求解的是前车紧急停车时，后车在经过反应时间τ后也采取紧急停车，恰好不追尾所采取的速度。在经典的Gipps模型中，车身的长度没有被考虑到，也没有考虑到实际跟驰过程中前后两车的时变速度，本文对经典Gipps模型进行改进，如图4所示。

图4 安全距离

后车紧急制动距离为：

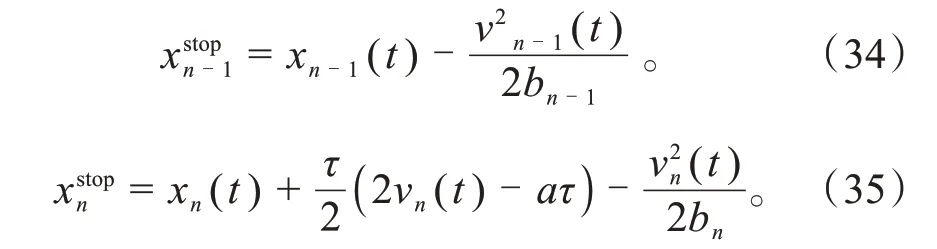
式中：xstopn-1为前车从采取制动动作到车辆停止期间行驶过的距离；xstopn为后车从采取制动动作到车辆停止期间行驶过的距离；xn-1（t）为前车在t时刻的位置；x（t）为后车在t时刻的位置；vn-1（t）为前车在t时刻的速度；v（t）为后车在t时刻的速度；bn-1为前车最大制动加速度；b为后车最大制动加速度；a为后车实时加速度；τ为后车的反应时间。

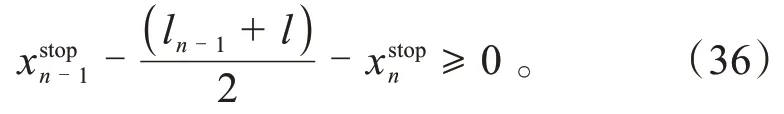
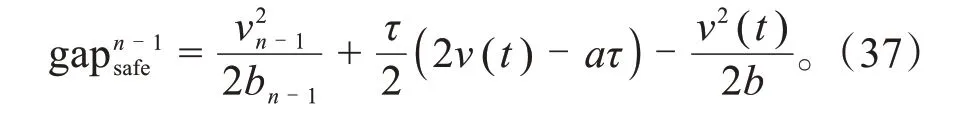
式中：ln-1为前车长度；l为后车长度。

由此计算公式，得到SV与其他3辆车的安全距离为：

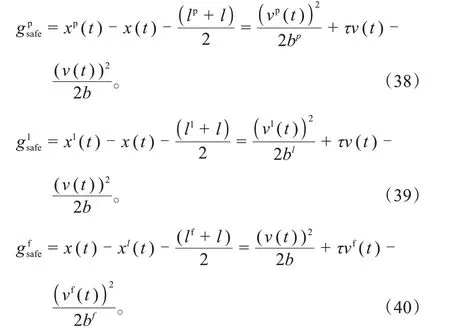
式中：xp（tstop）、x（tstop）分别为车辆PV和车辆SV紧急制动时的纵向坐标；xp（t）、x（t）分别为紧急制动开始时车辆PV和车辆SV的纵向位置坐标；vP（t）、v（t）分别为车辆PV和车辆SV的速度；bP、b分别为车辆PV和车辆SV的最大减速度；τ为车辆的反应时间；xl（t）为车辆LV的纵向位置坐标；vl（t）为车辆LV的速度；bl为车辆LV的最大减速度；ll为车辆LV的车身长度；lf为车辆FV的车身长度；xf（t）为车辆FV的纵向位置坐标；vf（t）为车辆FV的速度；bf为车辆FV的最大减速度。

车辆换道的安全性与车辆速度也有关，本文根据改进的Gipps安全模型计算车辆的安全速度。由式（37）的最小安全间隙gapn-1safe，推算出车辆n的安全速度范围。车辆n受到车辆n-1影响的最大安全速度vn-1n(t)为：

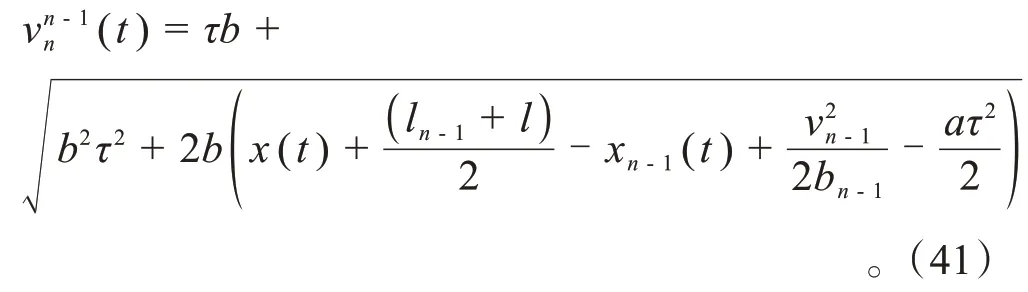
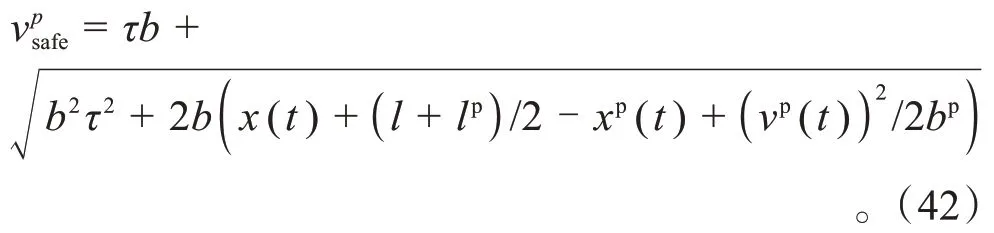
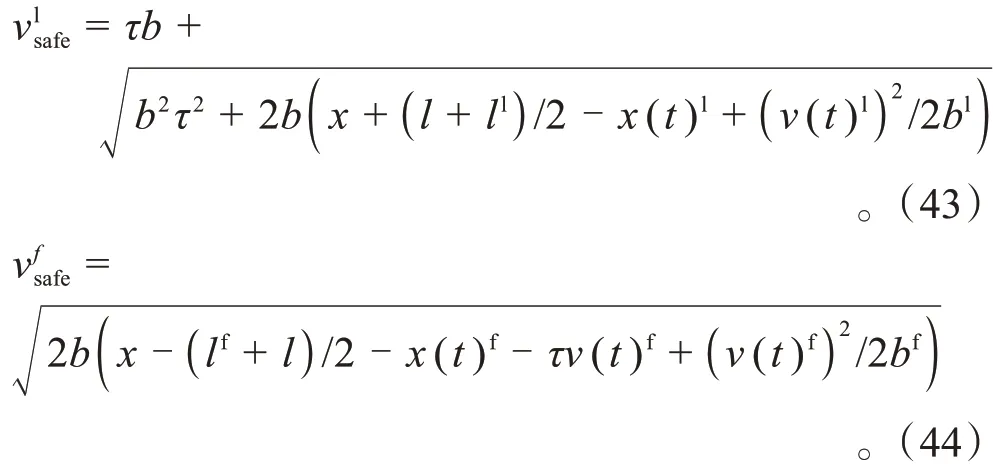
2 仿真验证

2.1 数据介绍

本模型使用的是美国联邦高速公路公布的NGSIM （Next Generation Simulation）数据［19］。NGSIM数据依据其真实性、高可靠性和高精度的特点，广泛用于自动驾驶的各类应用和交通研究领域，是目前行业内较为权威的车辆行驶数据。NGSIM数据是使用摄像头来搜集的交通信息，其中包括车辆的位置、速度、车型、车道等，时间的分辨率为0.1 s。数据采集选用的两段高速公路路段如图5所示。

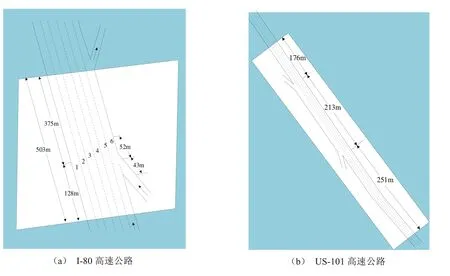
图5 NGSIM数据收集场景图

2.2 训练结果

根据Kolmogorov［20］定理，本文构建的网络为3层神经网络，包括一个输入层、一个隐藏层以及一个输出层，隐藏层节点个数l是根据输出层节点个数决定的，通过经验公式确定l的值，其中经验公式为：

式中：n为输入层神经元的数量；m为输出层神经元的数量。

本文在以上定理的基础上，拟用典型的非线性函数—对数函数对神经网络进行参数调优，对在以e为底x的对数函数，将嵌入神经网络前后拟合的结果进行对比。本次试验使用的传统BP神经网络的参数是3层神经网络，其中输入神经元和输出神经元数量都是1，隐层神经元设置为90个，而本模型提出的神经网络第一级的参数和传统BP神经网络完全相同，第2级神经网络选择了一个已经对目标函数训练好了之后的4层神经网络，其中输入层和输出层神经元均为1个，两个隐层神经元均设置成90个。图6是传统BP神经网络和本文提出的神经网络对log（x）的学习结果，可以看出，在训练次数明显较少的情况下，嵌入神经网络后在精度方面明显优于传统神经网络。

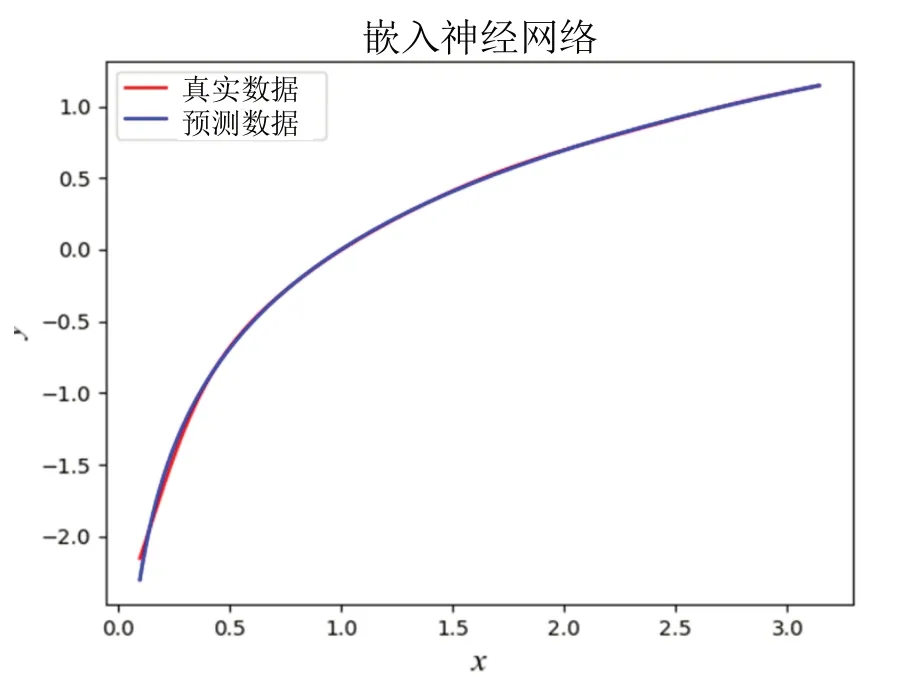
图6 非线性数据拟合结果

神经网络参数调整好后，对基于耦合深度学习-运动学的自动驾驶一体化换道模型进行训练和测试，本节共选用了100辆车的换道数据，其中70组数据作为训练集，剩余30组数据作为验证数据集。如图7所示，图中蓝色曲线表示本模型训练误差随着训练次数增加而变化的趋势，可知训练误差随着训练次数快速下降，训练超过20次时，损失值稳定并且趋于收敛。考虑时间成本和梯度下降所需的时间，将搭建的神经网络训练次数设置为25次。

图7 误差随训练次数的变化

图8为本模型预测的自动驾驶换道轨迹规划曲线，其中黄色曲线为原始轨迹曲线，蓝色曲线为本模型训练之后得到的学习结果。从图中细节可知，相较于车辆启动换道阶段，利用本模型可以更快地启动换道，其原因主要是机器决策所需的反应时间比人类决策所需时间缩短了；在换道过程中间阶段，车辆稳定地发生横向和纵向位移，总趋势同人类换道一致；在换道结束阶段，本模型更早地完成了换道，其原因也是在保证与后车安全性的前提下，及早完成换道，增大与前车的距离。由此可证明本模型可以规划出平滑的轨迹曲线，且由于缩短了反应时间和人为差异等因素，使换道过程变得更可控、更高效。

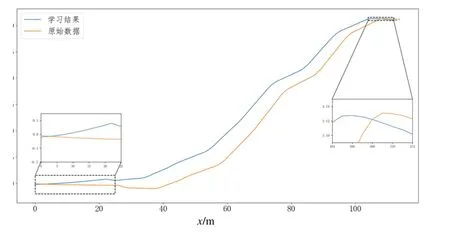
图8 车辆成功换道场景仿真

2.3 误差统计

为了直观地体现训练数据和原始数据的区别，本节摘抄部分名义值和预测值数据，如图9和表1～3所示。

图9 NGSIM原始数据

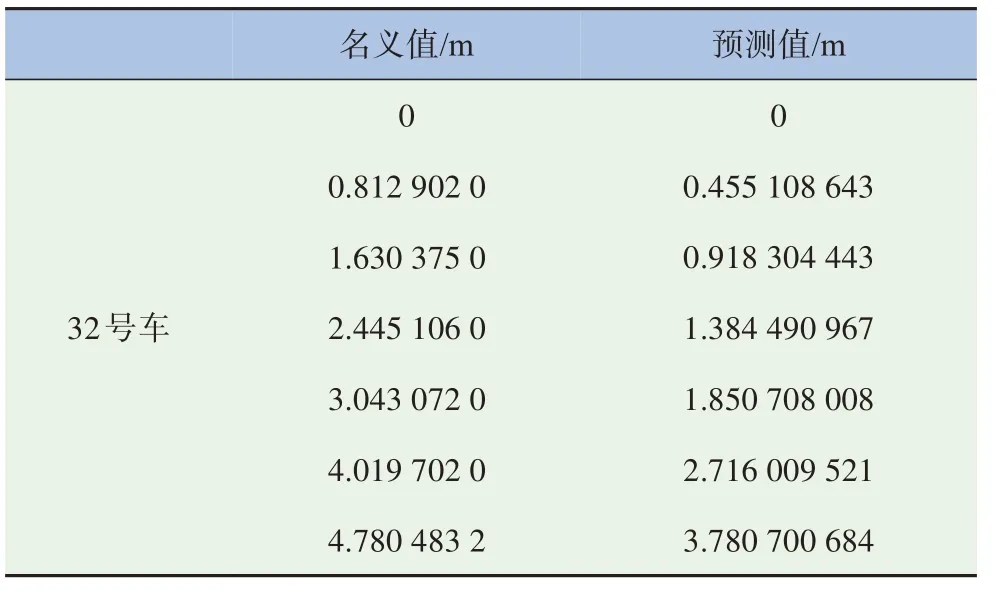
表1 32号车横向位移对比表

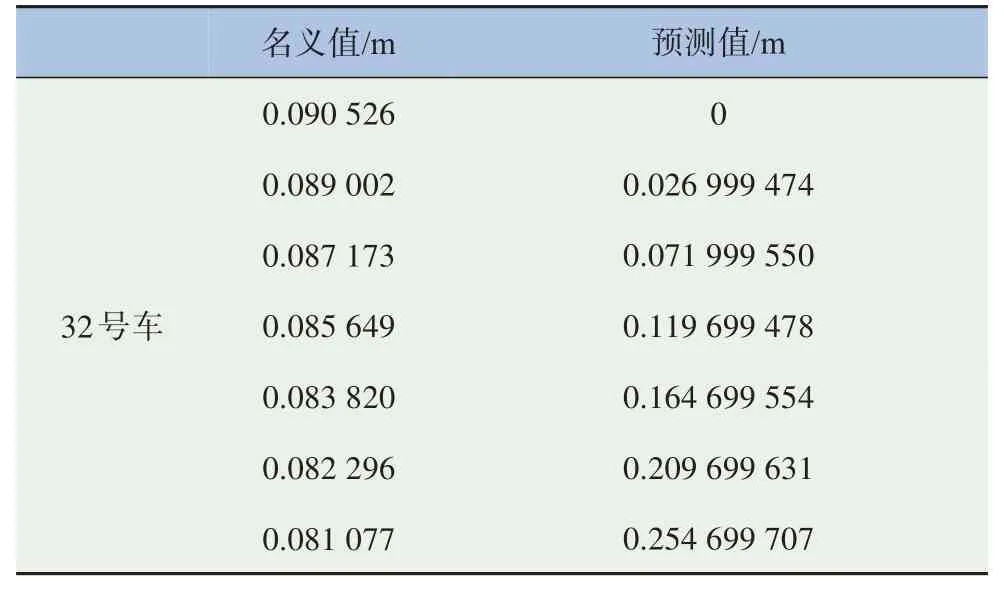
表2 32号车纵向位移对比表

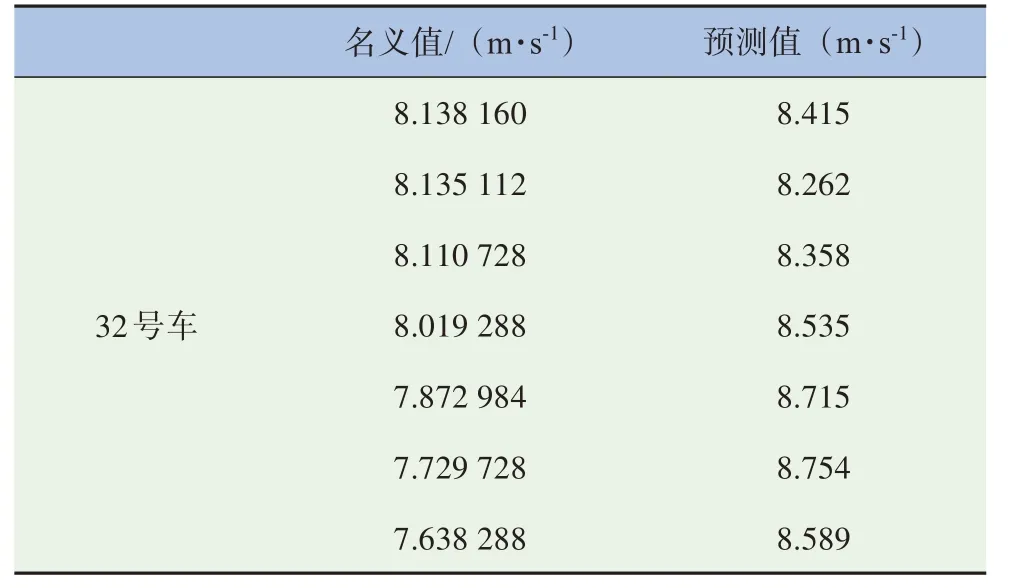
表3 32号车速度对比表

本节使用了70组换道数据进行训练和验证，拟用平均绝对误差（Mean Absolute Error，MAE）以及平均绝对相对误差（Root Mean Squared Error，MARE）这两个统计学中常用的统计量对模型进行误差统计。

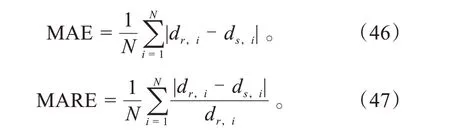
式中：N为测试数据样本数；dr，i为第i辆车的名义值；ds，i为第i辆车的预测值。

针对实际情况，做如下定义：MAEreal和MAREreal分别表示预测值与名义值的平均绝对误差和平均绝对相对误差，这两个统计量可以表征实际值和预测值的误差。

本节对基于嵌入神经网络训练之后的一万余条预测数据和原始数据进行比较，结果见表4。

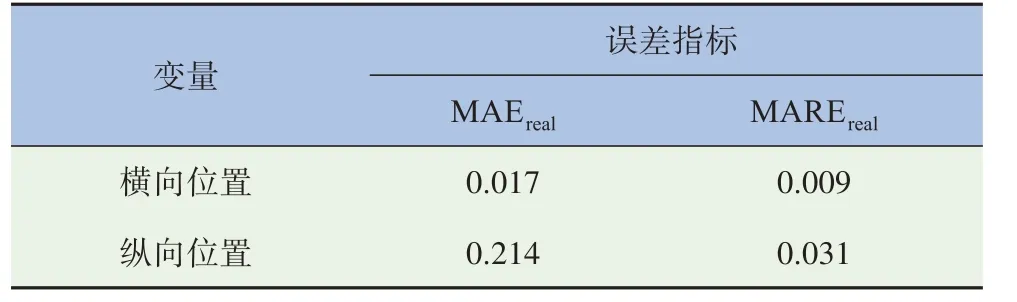
表4 误差对比表

2.4 基于CarSim的仿真验证

CarSim是用于车辆动力学的专用仿真软件，该软件可以对驾驶员、路面条件以及空气动力等方面进行仿真输入，对车辆制动性、稳定性参数等进行输出。CarSim可以方便灵活地定义试验环境和试验过程［21］。

将提出的深度学习模型输出的车辆轨迹数据作为CarSim输入，拟用该软件对模型轨迹进行可跟踪性、平稳性等参数的评估。

本节对训练的70组车辆换道轨迹随机选择一组输入到CarSim仿真软件中进行动力学仿真，图10为车辆SV在成功换道场景下本模型预测模型的仿真结果。图10a为车辆SV在成功换道场景下，本模型输出轨迹的仿真结果，其中蓝色曲线为本模型输出的轨迹，亦即目标轨迹，红色轨迹是CarSim仿真条件下的跟踪轨迹，从图中可知，本模型输出的轨迹在动力学仿真中变化平稳，可以和目标轨迹保持较小误差的条件下被跟踪。图10b为车辆SV在成功换道场景下，本模型输出速度的仿真结果，其中蓝色曲线为本模型输出的速度，即目标跟踪速度，红色曲线是CarSim仿真条件下的跟踪速度，由图可知，本模型输出的速度在动力学仿真中在驻点以及拐点处同目标速度有一定差异，但是同样较为平滑，在可接受的范围内。图10c为换道过程中车辆前轮转向角随时间变化情况，红色曲线代表了车辆的右前轮转向角变化情况，蓝色曲线代表了车辆的左前轮转向角变化情况，车辆在换道准备阶段前轮转向角为0，在换道执行阶段，车辆前轮由0逐渐增大到最大值后，逐渐减小至0，然后向相反方向行驶至较大值后减小至0。此外，车辆左前轮与右前轮的转向角存在差异，与车辆真实换道情况相符合。图10d显示了车辆轮胎的侧向滑移角，4个车轮的变化保持一致，变化的数值较小。

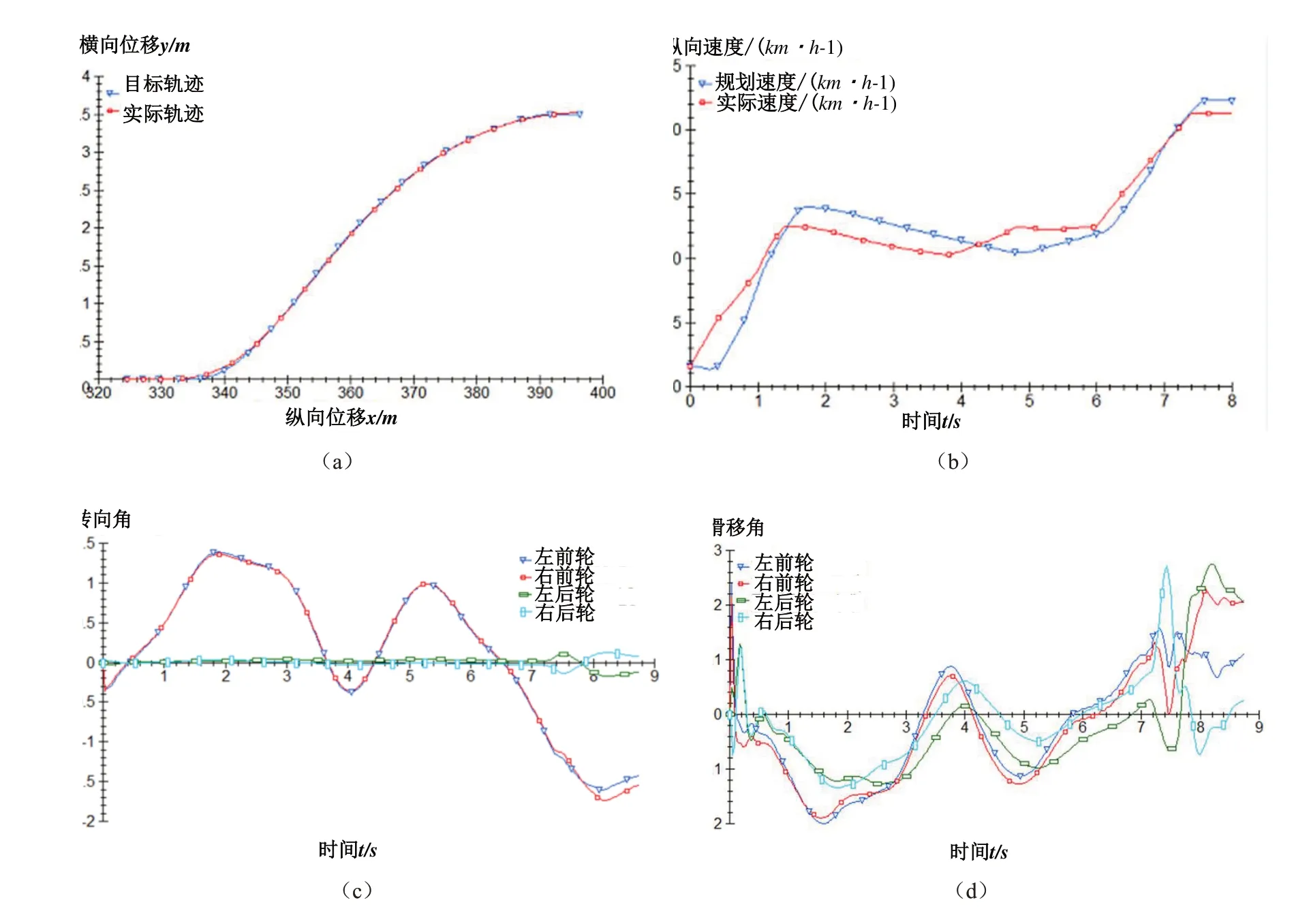
图10 车辆成功换道场景各参数图像

为了对比曲线的平滑程度，本节将原始数据中的加速度值和神经网络预测结果进行对比，可见，本模型预测加速度较真实平均值结果较小，结果见表5。

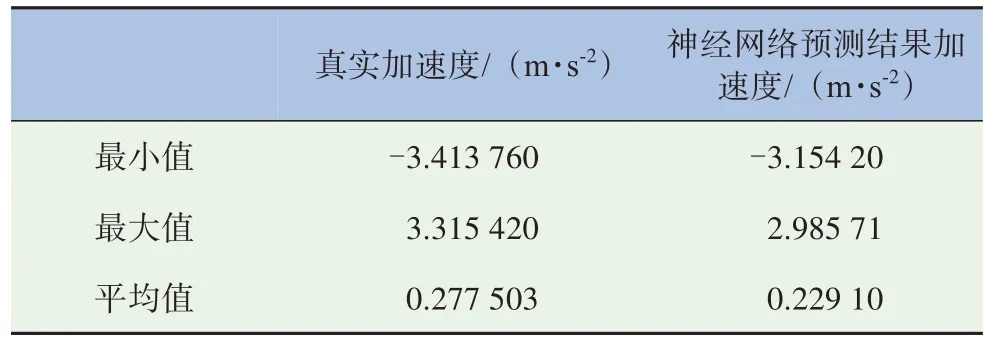
表5 加速度对比表

3 结论

本文提出的自动驾驶领域提出一种耦合深度学习-运动学的自动驾驶一体化换道算法，建立了嵌入神经网络模型，并综合考虑了目前主流换道模型的不足，从而引入基于规则的训练模型，对于有限数据下神经网络如何能适应和学习到更多驾驶技巧的问题提出了解决思路。得到以下主要结论：

（1）利用本模型可以规划出一条合适的自动驾驶车辆换道轨迹，且能保证换道车辆能够更安全、更舒适地完成换道。

（2）仿真发现，构建的换道轨迹规划模型可以用于自动驾驶车辆换道的场景。车辆可以在有限的数据量条件下对新的交通场景做出合理的反应。

（3）CarSim的仿真显示，本章节提出的模型所规划出的换道的轨迹和速度能够被自动驾驶车辆跟踪，车辆行驶稳定性良好。