基于车辆动力学模型的换道轨迹规划研究

曾望云，隗寒冰

（1.中国汽车工程研究院股份有限公司，重庆 401122；2.重庆交通大学机电与车辆工程学院，重庆 400074）

近5年来，国内自动驾驶汽车已经逐步用于特定区域的示范应用，Robotaxi的规模化测试推广加速推进，自动驾驶车辆应用前景明朗。与人工驾驶相比，自动驾驶具有操作快速、准确，有望提高驾驶安全性、舒适性和交通效率。其中，自动驾驶车辆决策规划模块类似人类大脑，先对当前环境做出分析判断，然后对底层控制模块下达指令。

国内外学者对自动驾驶车辆换道行为的研究主要集中在换道决策模型和换道轨迹规划方法上。RACHAEL等［1］基于搜索的轨迹规划方法源自机器人学，先对周围环境进行描述并建立自主车辆的工作空间，然后根据约束条件对轨迹进行搜索获得符合要求的轨迹簇，并选出最优轨迹。MINT等［2］提出了采用微分理论规划换道路径，考虑车辆动力学约束，但计算量庞大、实时性差。BLANK等［3］采用最小曲率半径方法设计了紧急避让路径，此方法能保证车辆整个换道过程路径最短，但没有考虑其他的约束条件。李玮等［4］以四段式车道变换理论为基础，对传统换道轨迹进行二次规划，给定了车辆换道轨迹的性能评价函数，可以较好地克服传统换道轨迹模型的缺陷，但是仅从轨迹特性上出发，并未考虑横摆角速度等车辆动力学特性。CHOI等［5］利用Bezier曲线对自主车辆路径进行轨迹规划，得到的换道轨迹平滑，过渡平稳且曲率连续，但是并未对Bezier曲线控制点的选取进行分析，也没有考虑车辆的横向加速度限制。HUANG等［6］提出了一种将轨迹规划问题转化为对可驾驶区域电路图网格划分问题，采用局部电流比较法寻找无碰撞路径以实现自动驾驶车辆避障换道轨迹生成。LIM等［7］基于曲线坐标系进行了最优轨迹规划，在横向轨迹规划中将横向轨迹的终点状态采样划分为超车、跟随、换道3种状态，在纵向轨迹规划中考虑与障碍物的潜在碰撞，将纵向规划问题定义为具有二次成本函数和边界条件的模型预测控制问题，通过线性模型预测控制优化了车辆的纵向轨迹。游峰等［8］分别以几何曲线与多项式曲线生成的换道轨迹进行了对比分析研究。王海等［9］提出一种新的改进余弦换道模型，采用多项式来描述换道轨迹，提出基于评价指标的边界条件选取最优轨迹。聂枝根等［10］提出了自动驾驶汽车变道动态轨迹规划算法，设计了兼顾变道效率和乘员舒适性的优化目标函数，优化获得了在变道轨迹最大纵向长度范围内的实时动态最优变道轨迹。WANG Hong等［11］提出了运用模型预测控制原理实现在不可避免的碰撞情况下生成可能减少碰撞路径的运动规划方法，其中的目标函数设计考虑了参与车辆的碰撞严重程度估计、道路边界约束、障碍物的人工势场定义及轨迹跟踪性能要求等车辆相关限制因素。

为了安全快速地将自动驾驶车辆从当前位置导航到目标点，既要考虑车辆动力学要求又要适应极端工况下的换道轨迹规划，提高自动驾驶车辆运动规划算法的操纵稳定性。本文区别于各类基于图搜索、曲线拟合等抽象的理论推导方法，考虑车辆动力学、轮胎特性以及路径规划，同时运用侧向加速度安全分析法求得前轮转角与车速的变化关系来定义横向控制序列的最大前轮转角范围，设计满足约束要求的目标函数，以对轨迹进行综合评价选优，从而满足换道过程的操纵稳定性。为验证所设计的基于车辆动力学模型的换道轨迹规划方法的可行性及效用，通过CarSim/Simulink联合仿真平台下进行了试验，以模型预测控制方法构建轨迹跟踪控制系统，并与曲线坐标系下最优规划方法所规划的换道轨迹对比其跟踪效果，结果表明，该算法能有效提高规划轨迹的操纵稳定性，还可实现冰雪路面等极端工况下自动驾驶车辆换道轨迹的最优规划。

1 系统框架

为保障自动驾驶车辆在极端行驶工况下的稳态特征，本文从车辆动力学角度出发，设计了基于车辆动力学控制序列采样的换道轨迹规划方法。所设计的换道轨迹规划系统依据其功能可划分为车辆动力学模块、轨迹生成模块和目标函数优化模块，该系统框架及轨迹规划过程如图1～2所示。

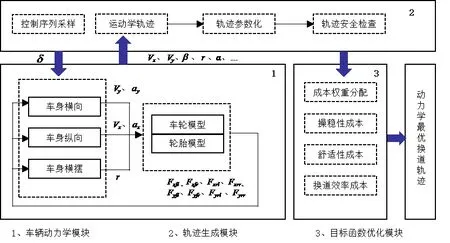
图1 轨迹规划系统框架

该换道轨迹规划系统接收到来自行为决策系统的换道指令后进行换道轨迹规划任务。在单一规划周期τ内，车辆动力学模块首先以轨迹生成模块的前轮转角采样序列δ={δ0，δ1，...，δn}为输入，经车辆动力学模型推演，输出离散时间下的车辆纵向速度Vx、横向速度Vy、横向加速度ay、横摆角速度r、横摆角加速度r'、各车轮侧偏角α状态，经运动学轨迹转化关系求得包含车辆状态信息的换道轨迹点序列p={(x0，y0)，(x1，y1)，...，(xm，ym)}，并将轨迹点信息参数化为图2所示的连续蓝色虚线轨迹ζ={ζ0，ζ1，...，ζn}。

图2 轨迹规划过程

为满足轨迹的安全性要求，还需通过轨迹安全检测模块剔除未达到安全标准的轨迹后交由目标函数优化模块，依据车辆模型输出的质心侧偏角β、横摆角速度r、轮胎侧偏角α等离散状态结合目标函数优化方式对轨迹序列进行优化，筛选出当前规划周期内的最优轨迹，并由跟踪控制系统完成轨迹跟踪任务，再执行下一周期的换道轨迹规划任务。

最终在n个规划、控制周期的循环往复后，规划出以红色实线示意的包含车辆动力学特征最优换道轨迹，完成整个换道过程。

2 车辆动态轨迹规划

2.1 车辆动力学模型构建

车辆动力学模型作为换道轨迹规划系统的核心，既需体现较为完整动力学特征，同时还需考虑规划算法的实时性而应具备较低的复杂度，所以本文选用车辆7自由度模型构建系统的车辆动力学模块。该模型包含横向、纵向、横摆运动及各车轮转动的7个自由度，相比于车辆2、3自由度模型更能完整地描述车轮-车身状态，且相比于14自由度及更高自由度的车辆动力学模型更易于求解，相关7自由度车辆动力学模型受力分析如图3a所示。

纵向、横向及绕Z轴方向的相关力平衡方程表示为：

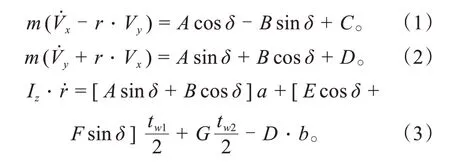
式 中：A=Fxfl+Fxfr、B=Fyfl+Fyfr、C=Fxrl+Fxrr、D=Fyrl+Fyrr、E=Fxfl-Fxfr、F=Fyfl-Fyfr、G=Fxrr-Fxrl；Vx及Vy分别为车身横、纵向速度；m为整车质量；r为横摆角速度；δ为前轮转角；a、b分别为前、后轴到质心的距离；Iz为绕Z轴的转动惯量；tw1、tw2分别为前、后轴轮距；Fxfl、Fxfr、Fxrl、Fxrr分别为左前轮、右前轮、左后轮、右后轮的轮胎纵向力；Fyfl、Fyfr、Fyrl、Fyrr为对应车轮的轮胎横向力。

车辆正常行驶时，各车轮上存在如下力矩平衡如图3b所示，可表示为：

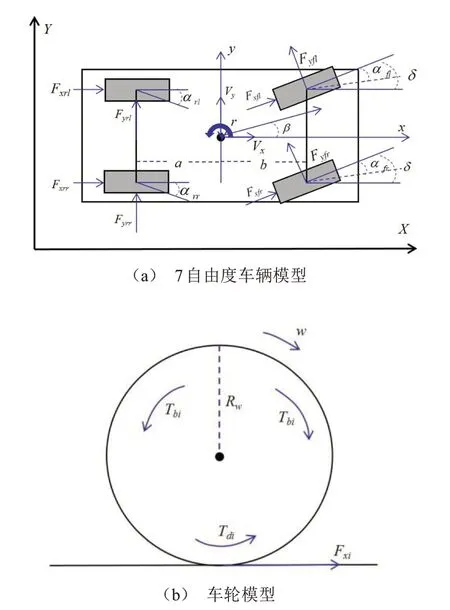
图3 车辆及车轮模型

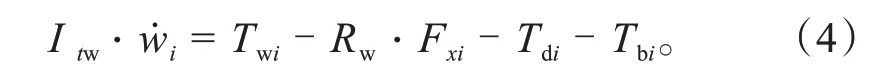
式中：Itw为车轮的转动惯量；wi为对应车轮转速；Rw为车轮滚动半径；Twi、Tdi及Tbi分别为对应车轮的输出力矩、滚动阻力力矩及制动力矩，i可对应表示为左前轮fl、右前轮fr、左后轮rl、右后轮rr。

通过建立Dugoff轮胎模型描述轮胎的非线性特征及滑移特性，其对应轮胎相耦合的纵向力及横向力可表示为：

式中：Cxi为轮胎的纵向滑移刚度；Cyi为横向转向刚度；Si为车轮滑移率；αi为轮胎侧偏角；λi为轮胎动态参数；μ为路面摩擦因数；Fzi为轮胎垂向载荷；εr为摩擦衰减系数。

建立好上述相关车辆及车轮、轮胎模型后，通过给定模型前轮转角输入，获取相关车辆状态，包括纵、横向速度Vx、Vy、质心侧偏角β、横摆角速度r以及各轮胎侧偏角αi等，并依据车辆坐标及局部坐标转化关系求得系统所需的轨迹点的坐标信息：

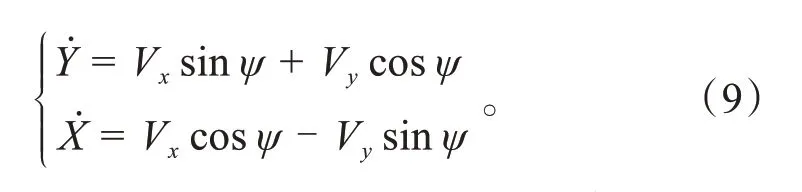
式中：X、Y为局部坐标系下的车辆位置信息横纵坐标；ψ为车辆的航向角。

依据表1中的相关车辆参数，在附着系数μ为0.8的干混凝土路面以及初始速度为20 m/s的初始条件下，输入连续变化的正弦转角分别得到CarSim模型、动力学模型2 s内的各状态对比情况，如图4所示。对比结果表明各模型输出的轨迹、横摆角速度、质心侧偏角、轮胎侧偏角误差均较小，验证了动力学模型的可靠性。通过输入固定前轮转角采样δsam，求解模型在1 s内的车辆行驶轨迹及部分相关状态，如图5所示，可以看出轨迹及各状态呈簇状，有利于进行各轨迹特征指标化。后续以目标函数评价的方式对换道轨迹选优，初步验证了以车辆动力学模型构建换道轨迹方法的可行性。

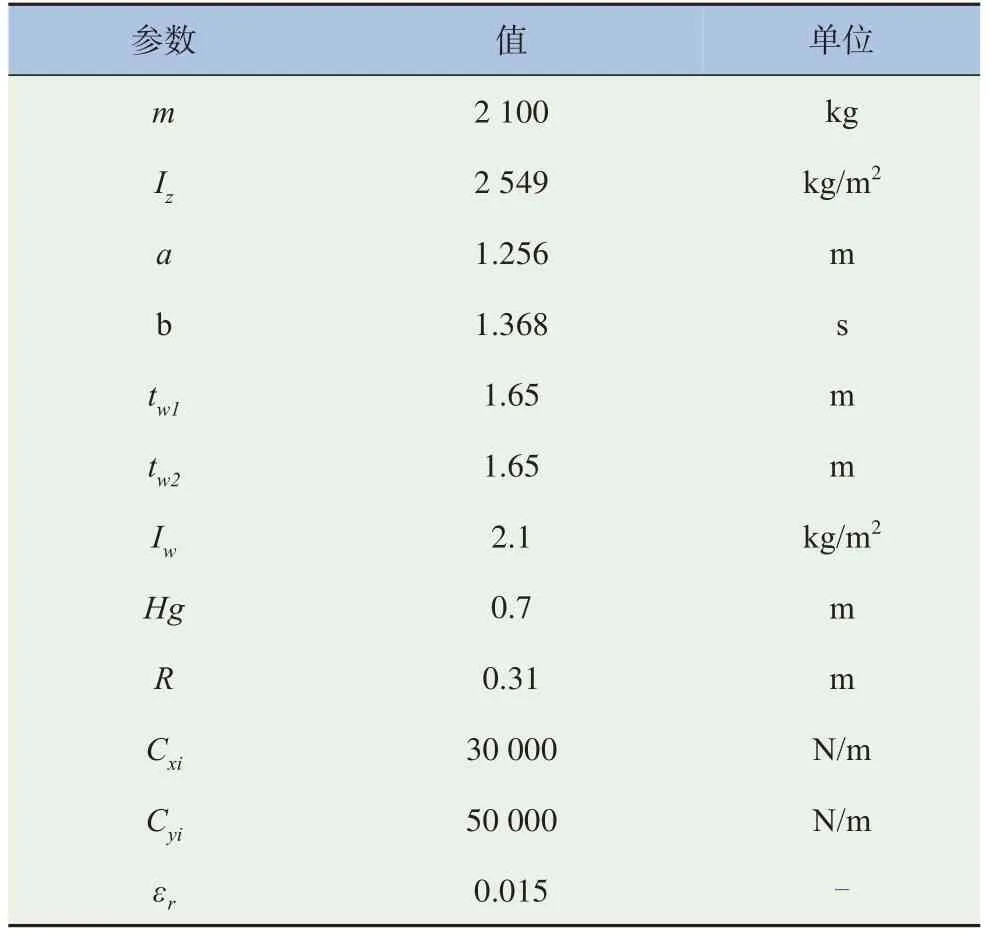
表1 相关车辆参数

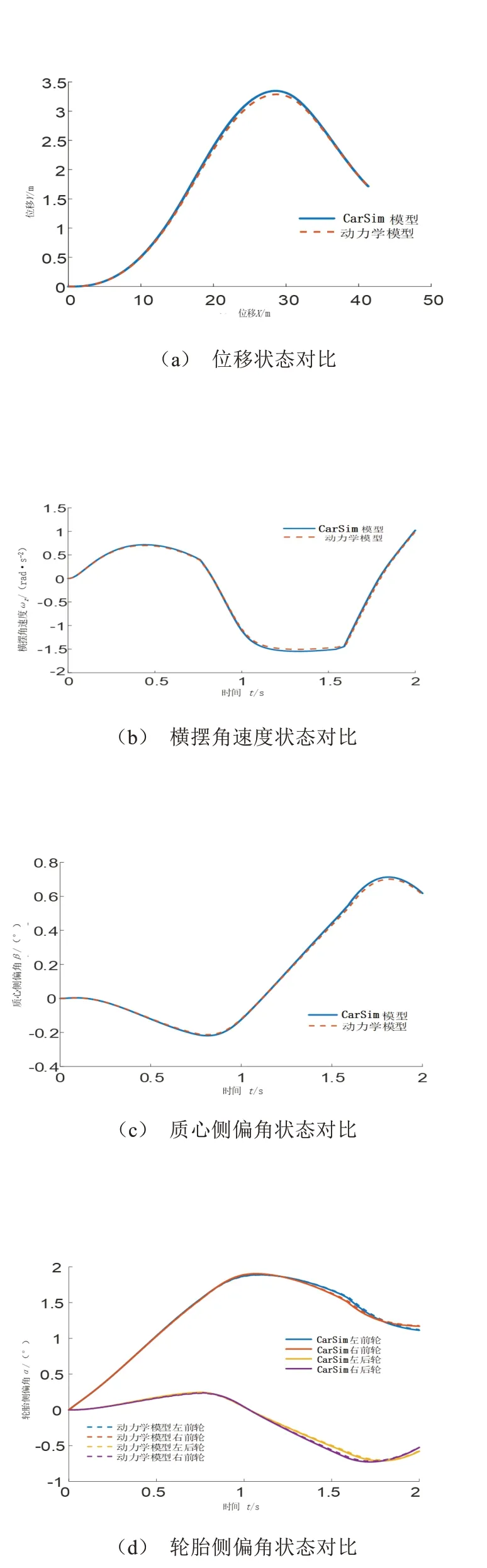
图4 模型各状态量对比情况

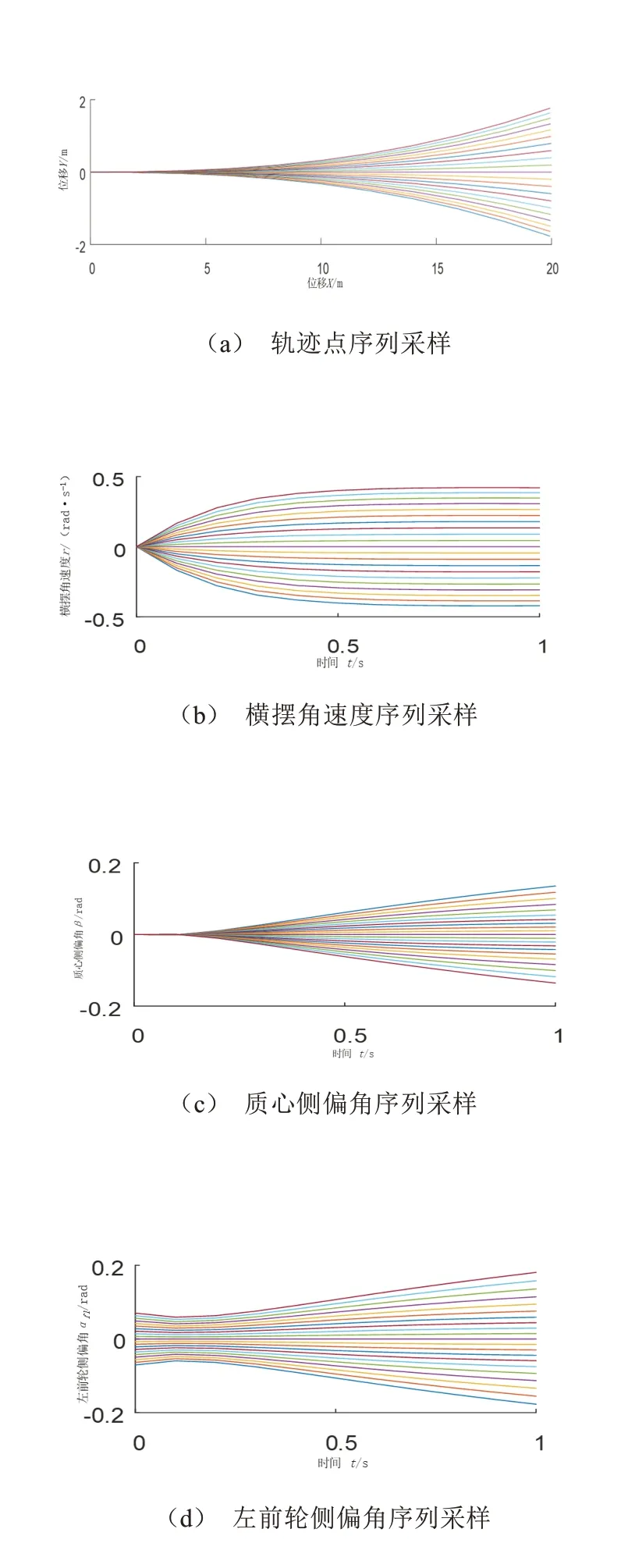
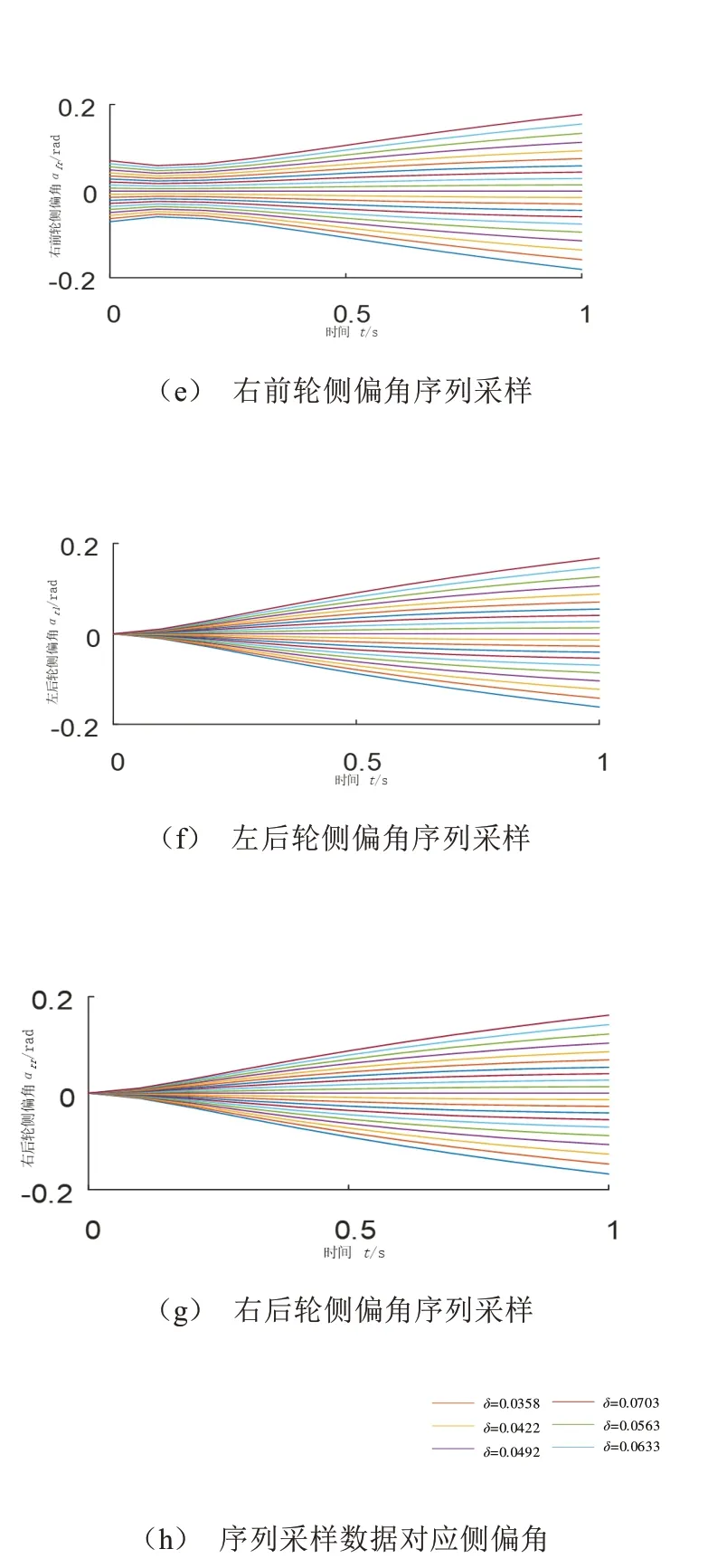
图5 车辆行驶轨迹及相关状态

2.2 横向控制序列采样

驾驶员在正常换道操作时，为配合车辆的实时车速需合理控制前轮转角大小，通常在较为拥挤的路段低速行驶时，为保证车辆的灵活性，需要输入较大的前轮转角；但在畅通无阻的中高速路段换道时，为保证车辆的稳定性，需小幅度控制前轮转角。因此，本文以运动学模型输入为依据，基于侧向加速度安全分析法，求得前轮转角与车速的变化关系，并用于定义横向控制序列的最大前轮转角。

在紧急工况下，为保证车辆的稳定与极限性能，需保证车辆转向换道时刻的横向加速度ay控制在限制级范围LL与最大级范围ML之内，其边界条件为［13-14］：

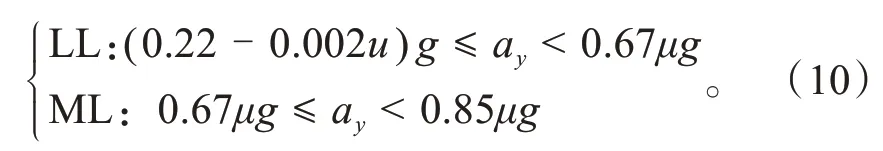
在紧急转向工况下，在较短的系统反应时间内，依据操纵稳定性2自由度车辆模型的运动微分方程，在稳态条件下可推导出：

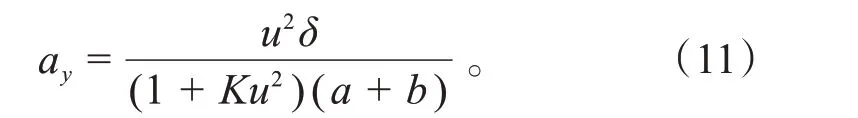
式中：K为稳定性因素；u为车速。

控制车辆转向的横向加速度在限制级上限0.67μg以内，则前轮最大转角δmax应满足如下条件：

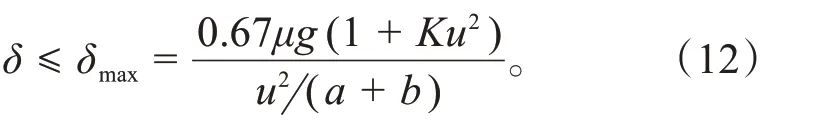
求得的不同附着系数硬路面上的最大前轮转角与车速关系如图6所示，车速与最大前轮转角呈反比例函数关系，且随着路面附着系数降低最大前轮转角随之减少，基本符合客观现实。

图6 前轮转角随速度的变化曲线

为获取模型输入的控制序列采样，需依据车辆当前车速及最大前轮转角随速度的变化关系求得控制序列的最大前轮转角δmax，并设定控制序列范围，选定合适的采样间隙Δδi，所定义的控制序列采样δsam表示为：

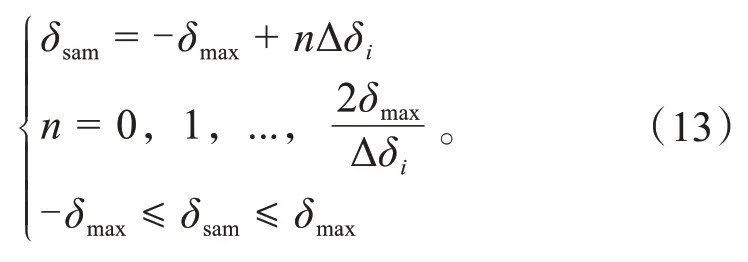
2.3 轨迹信息后处理

得到离散的车辆状态后，为保证换道轨迹的连续性及安全性，需对轨迹信息进行后处理。其中，单条轨迹ζi的基本信息可表示为：

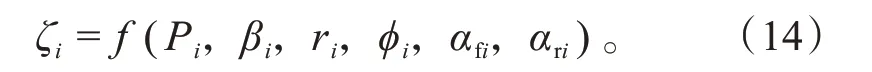
式中：Pi、βi、ri、φi、αfi、αri分别为单条采样轨迹各离散点的位置、质心侧偏角、横摆角、航向角及前后轮的侧偏角信息。

本文采用多项式曲线方式拟合车辆轨迹离散位置信息。多项式曲线函数的基本形式为：

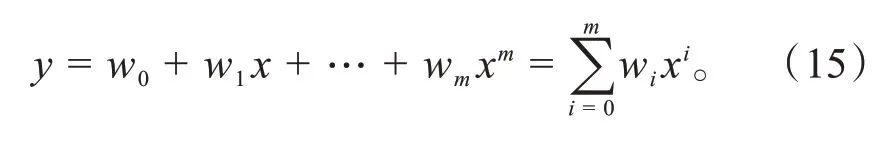
式中：wi为多项式曲线函数参数；m为函数最高指数幂。

在干混凝土路面上以车速u为20 m/s的行驶工况下，控制车辆动力学模型的最大限度前轮转角输入δmax为0.070 3，输出2 s内轨迹信息用于多项式曲线拟合。通过计算残差值e作为拟合后的曲线函数的评价指标，分别对比函数在最高指数幂为4次、5次、6次的拟合情况如图7所示。

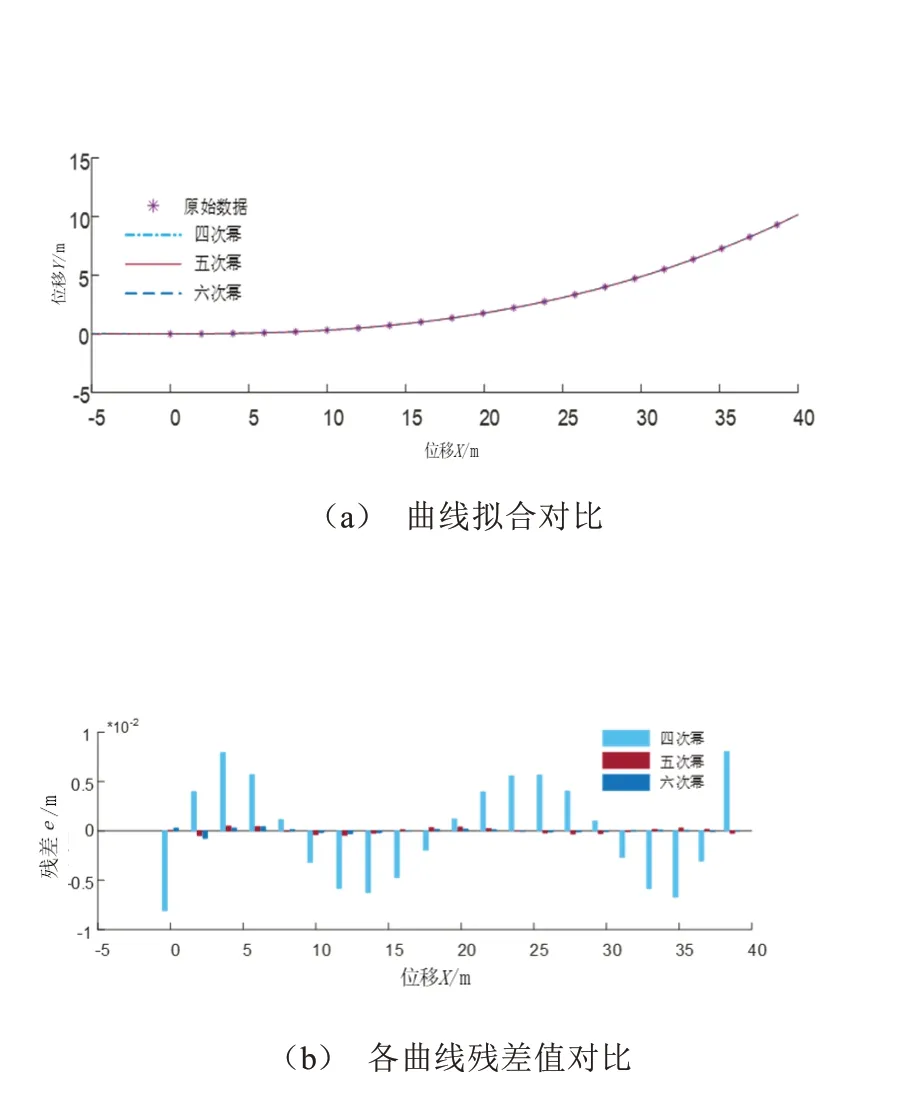
图7 各次幂函数拟合对比情况

由曲线拟合对比及残差值对比图分析可知，各指数幂曲线函数均能较好地拟合实际位置信息，且随着指数阶数的递增，拟合效果越好残差值越小。特别在4次幂提升到5次幂曲线残差值缩减明显，5次幂到6次幂的提升影响较小，结合NOROUZI等［15］对换道曲线函数得出的5次函数比其他换道轨迹函数具有更好的乘客舒适性结论，所以选用5次多项式函数作为换道轨迹拟合函数，则离散点的位置信息Pi也可表示为：

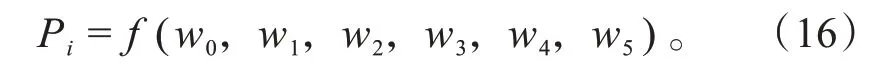
得到各采样拟合轨迹序列ζ后，还需对各轨迹信息进行限制，以剔除不符合最大曲率、超越换道边界、包含障碍物及临近障碍物的规划曲线，满足实际换道任务需求，保证换道过程的安全性，可设计其边界条件为：

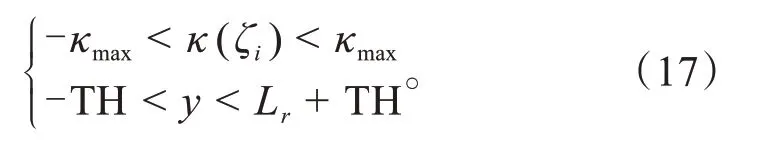
式中：κmax为曲率极限；y为轨迹横向距离信息；Lr为道路宽度；TH为规划轨迹允许的超越换道边界的阈值距离，该距离应保证小于道路宽度的一半。

2.4 目标函数设计

依据轨迹的相关状态信息可设计目标函数，以对轨迹进行综合评价选优，从而满足换道过程操作稳定性和舒适性要求。以下分别描述了构成目标函数的各目标项及意义。

以采样轨迹ζi位置信息Pi终点的纵坐标ye及终点的航向角信息φe定义特征目标Je，表征轨迹的换道效率：

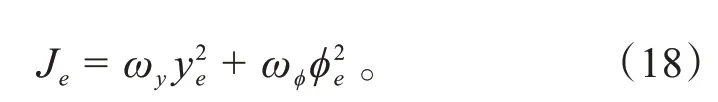
以单一采样轨迹ζi中各点的横向加速度ayij及航向角φij定义特征目标Jc，评价轨迹的舒适性：

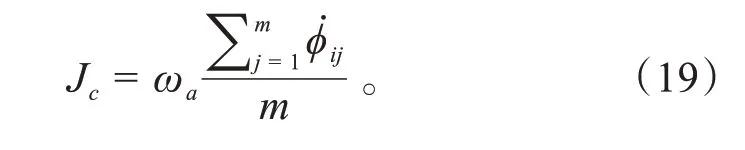
车辆的质心侧偏角βi、横摆角r及前后车轮的侧偏角αfi、αri状态影响车辆的稳定性，因而基于相关轨迹信息构建特征目标Js，评价轨迹的操纵稳定性：

式中：ωy、ωφ、ωa、ωβ、ωr、ωα分别对应各目标项的权重系数；ayij、φij、βij、rij、αfij、αrij代表其为第i条采样轨迹上第j个采样点的相关轨迹信息。

由于该方法所设计的换道轨迹并非由系统一次性规划完成，而是经由数个规划周期组合实现。各规划周期规划的轨迹序列大体一致，但不同规划周期下对轨迹的目标追求不一，为保障该方法的自由换道轨迹规划能力，需合理设计目标函数的权重配比，将表征换道效率的目标项Jc的相关权重ωy、ωφ设置为随车辆状态及换道位置动态变化，设计原理如图8所示。

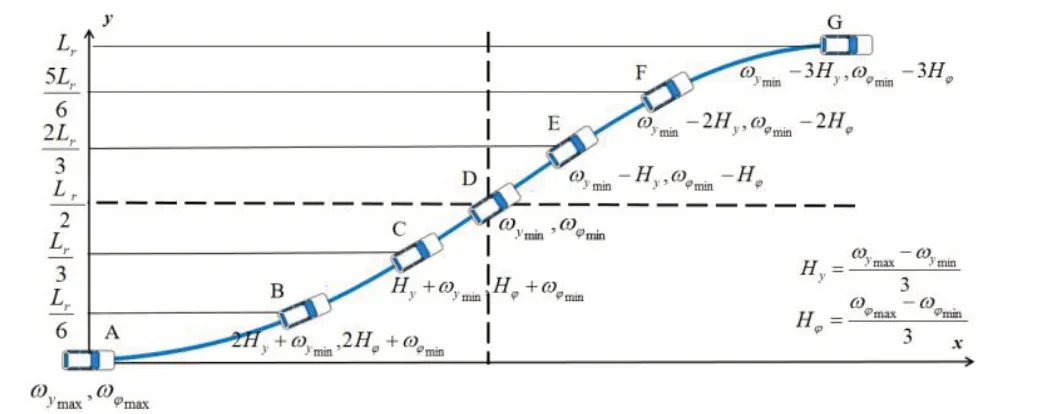
图8 权重设计原理

该设计原理仅考虑标准的一次换道仅跨越一个车道横向位置的情况，所以首先需将Lr定义为车道宽度，完成对ωy、ωφ最值的定义并计算得到A点到G点的权重值后，再以多项式函数拟合方式进行插值，最后将车辆当前的相对位置求得各位置的ωy、ωφ权重，其余特征权重ωa、ωβ、ωr、ωα以均等配比方式设定。完整的目标函数可以以式（18）的形式表示，通过目标函数J（ζ）计算当前规划周期下的轨迹簇ζ的各轨迹目标评分方式进行选优，即可规划出该规划周期下操纵稳定性最优轨迹。

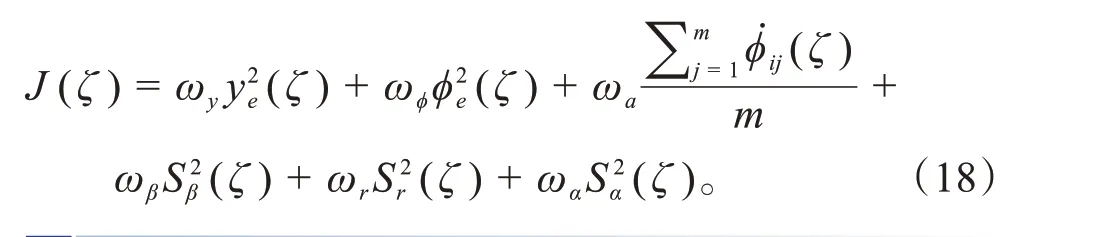
3 试验验证及分析

为验证所设计的基于动力学车辆模型的换道轨迹规划方法的可行性及效用，在CarSim/Simulink联合仿真平台下进行了试验，设定换道轨迹规划方法的预测时域为1 s，跟踪控制时域为0.5 s，车辆相关参数如表1中一致，其仿真工况为路面附着系数μ为0.3的冰雪路面，设定车速恒为72 km/h。为验证所设计算法在换道过程中操纵稳定性的优势，以模型预测控制方法构建轨迹跟踪控制系统，并与曲线坐标系下最优规划方法所规划的换道轨迹对比其跟踪效果。

对比两种换道轨迹规划方法情况如图9所示，两种方法均能实现轨迹规划任务。本文所设计的方法在经历共10次换道规划及跟踪控制过程后，完成了整个换道过程，所规划的轨迹更为平缓，规划时域更长，且对比表征车辆操纵稳定性的各轮胎侧偏角、横摆角速度及质心侧偏角状态峰值均有不同程度的降低，曲线变化更为平缓，优化了自动驾驶车辆换道过程中的车辆稳定性。

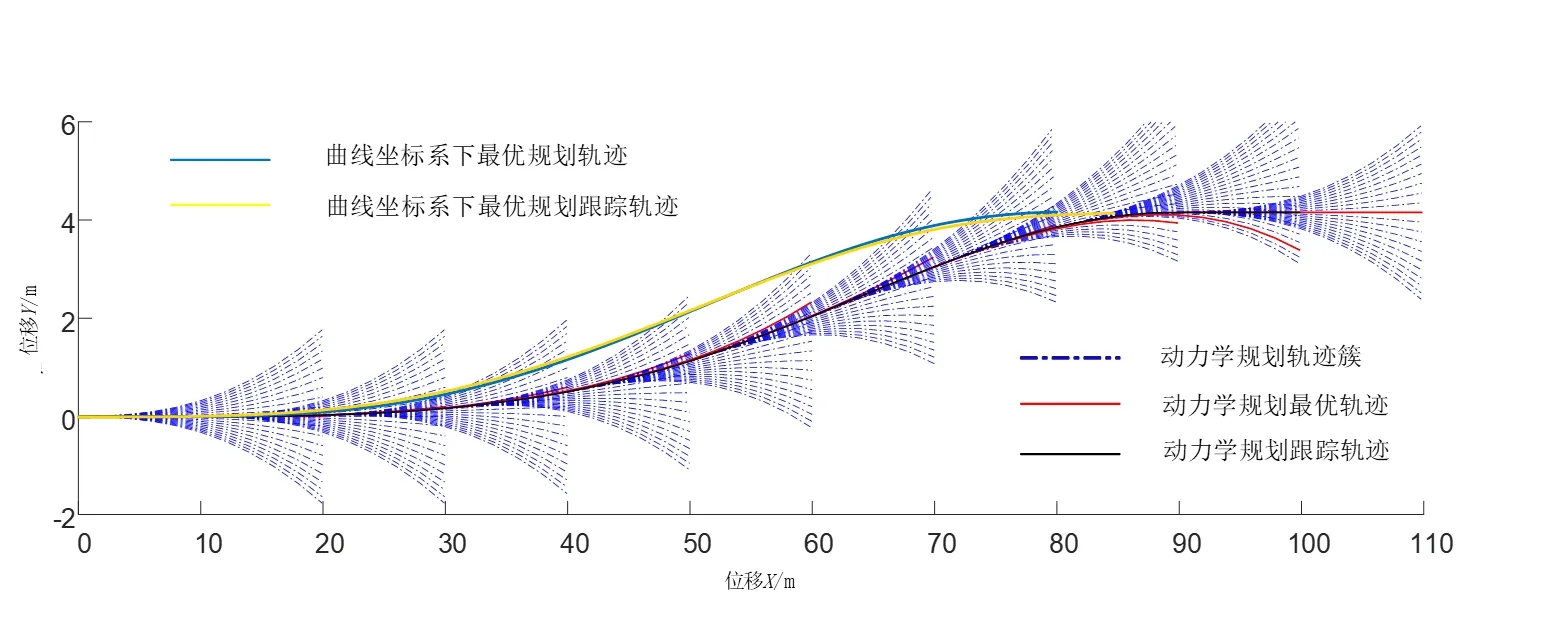
图9 换道轨迹规划对比情况

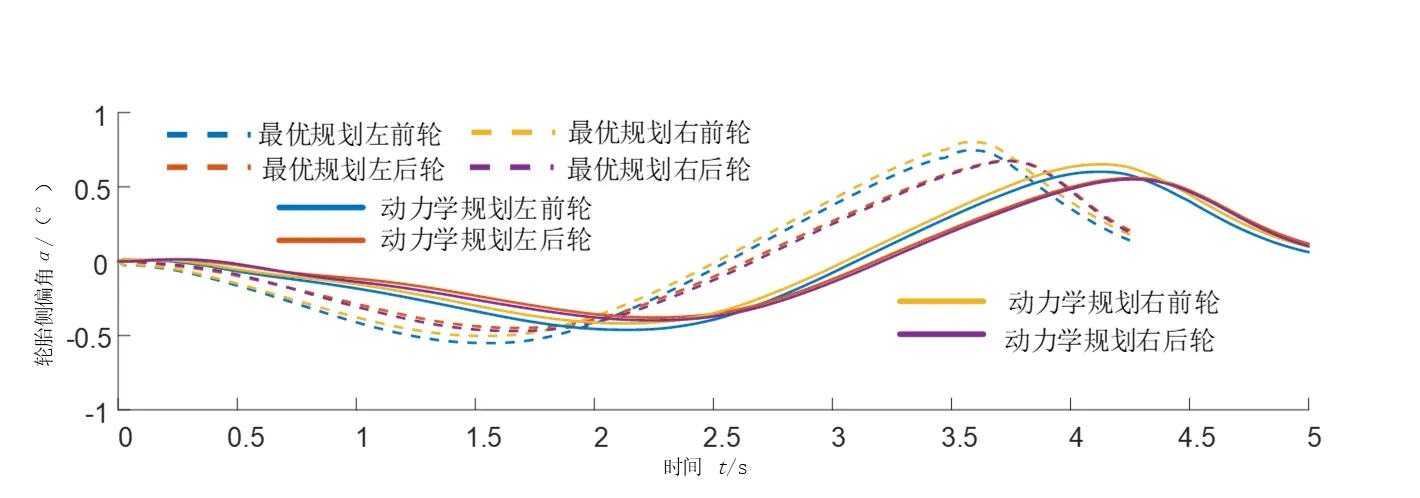
图10 换道过程轮胎侧偏角变化对比情况

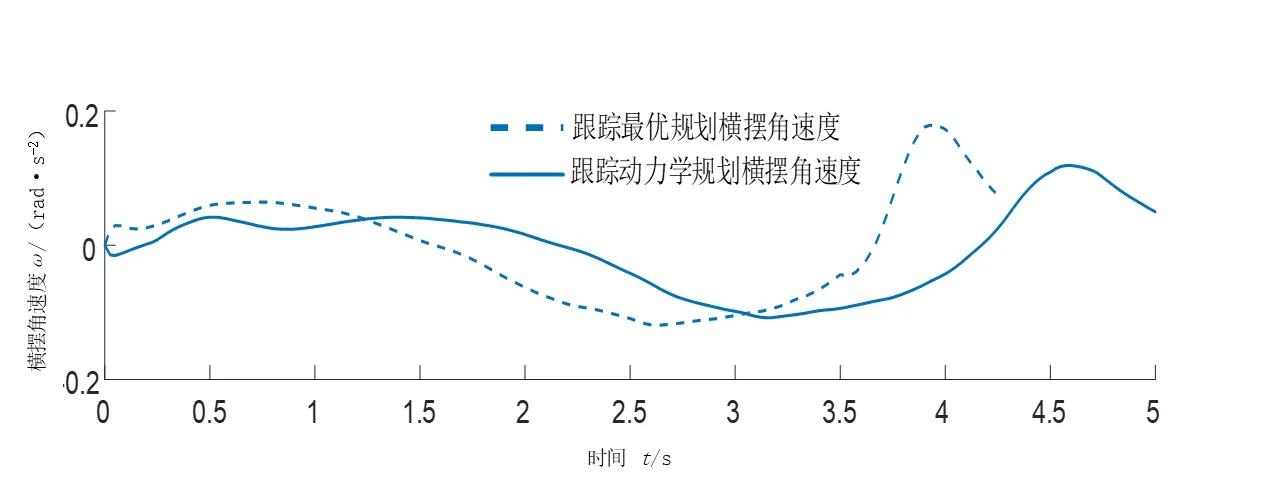
图11 换道过程横摆角速度对比情况

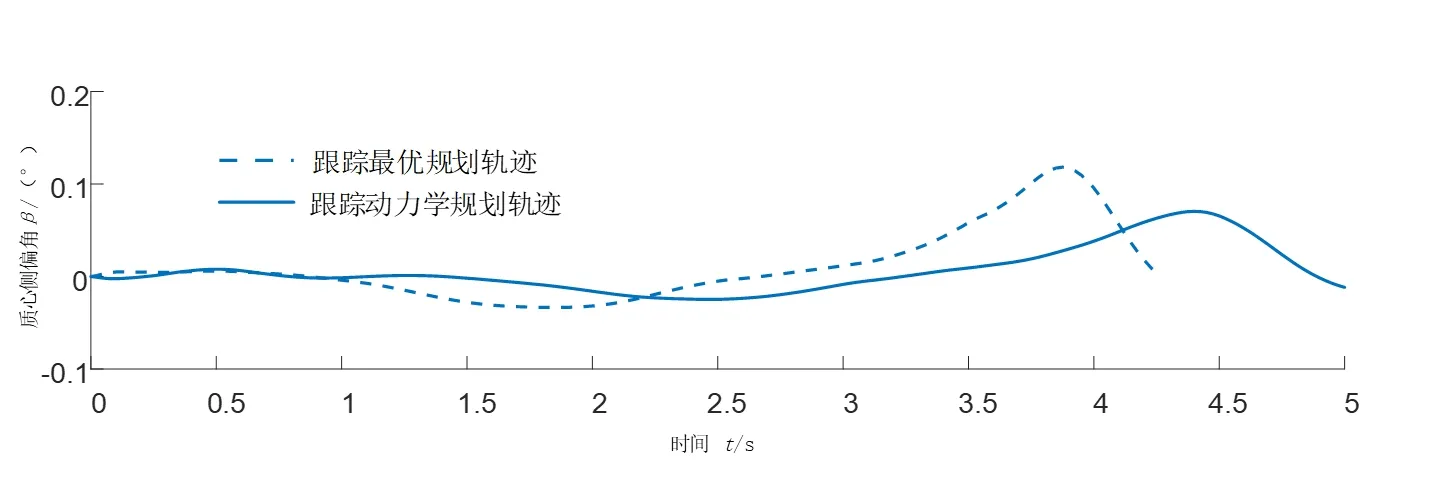
图12 换道过程质心侧偏角对比情况

4 结论

（1）横向控制序列通过车辆动力学模型、Dugoff轮胎模型进行采样，依据基于侧向加速度安全分析法求得前轮转角与车速的变化关系，定义横向控制序列的最大前轮转角，以满足在紧急工况下车辆的稳定性与极限性能。

（2）基于多项式曲线方式拟合车辆轨迹离散位置信息，剔除不符合最大曲率、障碍物及临近障碍物的规划曲线，满足实际换道任务需求。依据轨迹相关状态信息可设计目标函数，以对轨迹进行综合评价选优，从而满足换道过程的操纵稳定性。

（3）基于车辆动力学模型的换道轨迹规划方法的可行性及效用，在CarSim/Simulink联合仿真平台下进行了试验，最优规划方法所规划的换道轨迹更为平缓，规划时域更长，车辆操纵稳定性指标状态峰值均有不同程度的降低，还可实现冰雪路面等极端工况下自动驾驶车辆换道轨迹的精确性和操纵稳定性。