无人驾驶车辆解耦混合运动规划方法研究

王志琛，胡广地，刘建阳

（西南交通大学机械工程学院，成都 610031）

无人驾驶技术是当前汽车行业重要的技术发展方向之一［1-2］。运动规划通常是指在受限空间内通过一定方法寻找出一条能够在保障车辆和人员安全的同时满足舒适性和行车效率的最佳轨迹。在高速公路行驶场景中，运动规划面临的挑战主要体现在以下方面：首先，车辆高速行驶时需要更为苛刻地考虑车辆动力学特性；其次，运动规划方法在复杂约束下应规划出避免碰撞且高效、操纵稳定的轨迹，需要优先保证车辆避免碰撞；最后，高速无人驾驶车辆运动规划算法的实时性要求相比常速更高，所以算法要充分考虑合理降低计算的复杂性。

运动规划的抽象数学问题往往是求解一个以时间为参数的泛函优化问题［3］。由于一般高维受限优化问题的解不局限于某个函数，导致问题变得非常复杂［4］。目前，对于三维非凸优化问题的直接解法还比较复杂，主流方法是将其分解为横向偏移规划和纵向速度规划两个问题，也就是将运动规划进行横纵向解耦。

基于上述思想，可以在Frenet坐标系［5］中将问题简化表达，将运动规划问题进行横纵向解耦后可用现有算法进行求解，但是解耦降维也带来了一些信息的损失。进行横向规划时，时间信息的缺失导致无法完全表现出动态障碍物约束；进行纵向规划时，不在指引线上的障碍物很难表现出来，无法实现道路宽度上的全部障碍物约束。针对上述问题，现行的解决方法主要分为两种：第1种为并行多条指引线，即对每条车道生成一条指引线，并行使用最优化方法求解多条车道中的最优解，再进行横向对比选择［6-7］。此方法比较成熟，在城市道路复杂环境测试上取得了较好结果，对中低速复杂环境处理表现出色，但并行计算所带来的高计算量对速度较高、道路环境相对简单的高速公路行驶场景适用性不佳。第2种方法是根据交通环境、交通规则、自车状态（位姿、速度）等来确定与指引线对应的可使用空间参数，在决策阶段生成车道级决策，并在此空间上进行运动规划［8-10］。此方法能够避免大量的并行计算，在高速公路行驶场景中适应性较好，更符合无人驾驶规划系统层层优化的思想。但由于需要在决策阶段生成车道级决策，其上层决策算法相较于并行多指引线算法更为复杂。

基于以上问题，本文提出一种针对结构化道路高速（80～130 km/h）行驶场景的解耦运动规划指引线模型，在此指引线模型上表述运动规划所依赖的指引路径、决策信息和道路结构信息。其主要创新点为：提出一种横纵向解耦增强混合运动规划方法，横向规划中融合分段jerk规划算法［10］（Piecewise-Jerk Method，PJM）与多项式规划算法生成横向最优解逼近群，使局部路径满足2阶平滑，并使用代价函数和碰撞检测在最优解逼近群中选择轨迹，以优先满足高速运动规划中车辆避障的要求。在混合规划过程中，通过规划策略和参数优化降低最优解逼近群中的轨迹数量，进而降低算法的计算复杂度，以解决高速规划中高实时性要求的问题。

经在联合仿真平台中验证，证明本文提出的运动规划方法能在单条指引线的基础上，规划出优先满足车辆避免碰撞的可行轨迹，并且有效减少了最优解逼近群中的轨迹数量，相比于多车道分段jerk法混合最优轨迹生成法［9］（Optimal Trajectory Generation，OTG），此算法总时间复杂度降低了15%。

1 模型构建

1.1 解耦规划指引线模型

解耦规划依赖于Frenet坐标系，指引线作为Cartesian和Frenet坐标系之间的转换“桥梁”，其平滑性直接影响计算路径的质量［10］。解耦规划指引线模型RE定义为：

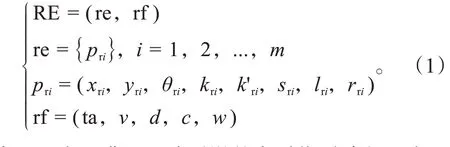
式中：re为已满足二阶平滑的实时指引路径，由m个分化为1 m间距的参考路径点pr组成；xri、yri、θri、kri、k'ri、sri分别为全局坐标系下第i个参考点的坐标位置、航向角、曲率、曲率变化率、里程；lri、rri为指引线左、右可规划区间宽度，其数值体现了在该段指引道路上是否允许被动变向其它车道；rf为参考线道路信息；ta为规划目标；v为参考速度；d为所在车道宽度；c为在指引线范围是否包含了可主动变道工况；w为车辆在指引线上的参考匹配点索引。

目前普遍认为运动规划处理时间在8 s左右或行驶距离在200 m左右较为合理［11］，综合工况和求解时间，本文取指引路径为220 m，由车辆定位点行驶方向前方的200个路径点及后方的20个路径点构成，即取m为221。

1.2 自车模型

自车模型主要包括车辆的定位模块所提供的位姿信息和车辆固有的外模型参数以及动力学参数。自车抽象模型E定义为：

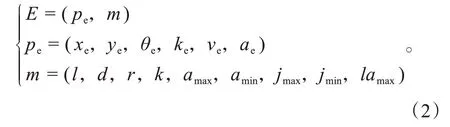
式中：pe为车辆位姿信息；xe、ye为车辆在全局坐标系下在道路平面的投影坐标；θe、ke、ve、ae分别为车辆在全局坐标系下的航向角、转弯曲率、速度、加速度；m为车辆固有参数；l、d、r分别为车辆长度、宽度及车辆后边界到车辆定位中心（后轴中心点）的距离；k、amax、amin分别为车辆标定允许最大转向曲率、最大纵向加速度、减速度；jmax、jmin、lamax为纵向jerk最大值、最小值及最大横向加速度。

1.3 障碍物模型

在运动规划中可将障碍物分为两类，即静态障碍物和动态障碍物，两者均可抽象表示为道路平面上的矩形。障碍物抽象模型O定义为：

式中：Os为静态障碍物的集合；Obsi为第i个静态障碍物；Od为动态障碍物的集合；Obdi为第i个动态障碍物；Obditj为第i个动态障碍物在tj时刻占据矩形的大小和位姿；ver1，ver2，ver3，ver4为障碍物矩形的4个顶点在道路平面上正投影点；cen为矩形中心点在道路平面的整投影点；θ为矩形的横摆角；l为矩形长度；d为矩形宽度；xveri，yveri为矩形顶点在全局坐标系下的坐标位置；xcen、ycen为矩形中心点在全局坐标系下的坐标位置。

2 运动规划解空间构造

运动规划中的解空间构造即道路与障碍物约束构造，将解空间分为横向规划L(s)的解空间构造和纵向规划S(t)的解空间构造，横向的解空间构造以参考线为基准进行Frenet坐标系的道路模型和障碍物转换，纵向的解空间构造以参考线为基准进行侵占参考线障碍物的Frenet坐标转换。

2.1 规划起点处理

对于规划起点，以定位点时间戳查询运动规划上一帧的输出轨迹，如果与定位数据位置误差小于阈值，则查询算法输出时间在上一帧输出轨迹所对应位姿信息作为规划起点，否则，以运动学模型预测规划为起点，规划起点ps为：

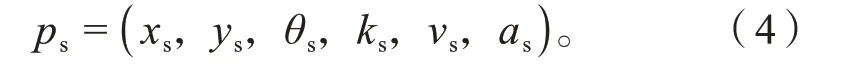
式中：xs、ys为车辆在规划起点位置的坐标；θs、ks、vs、as分别为车辆在规划起点的航向角、转弯曲率、速度、加速度。

利用式（5）［9］将规划起点转换到以指引线路径RE.re为基础的Frenet坐标系，得Frenet坐标系下规划起点psf如式（7）所示。

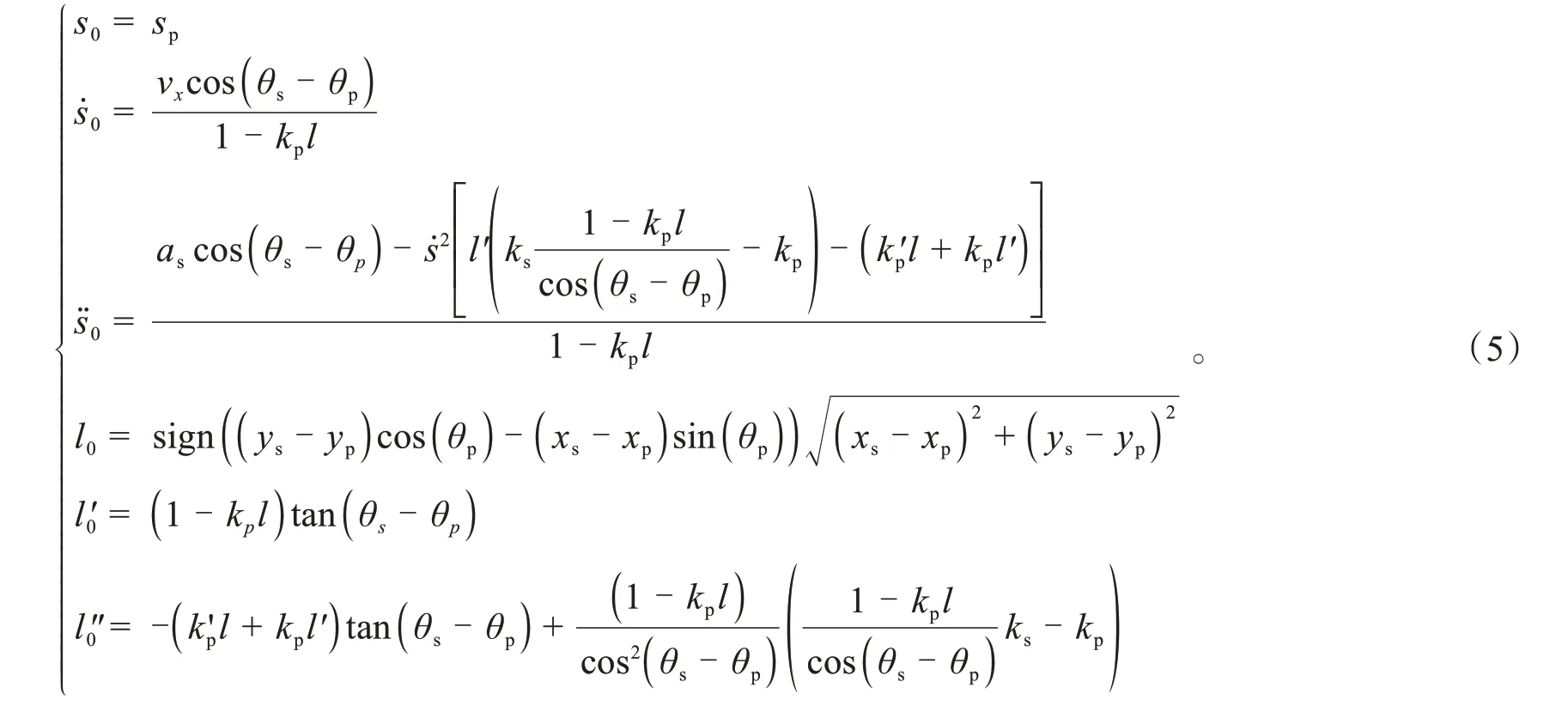
式中：pp为规划起点在指引线上的投影点，考虑路径在计算机表达中的离散性，pp由式（6）解得。

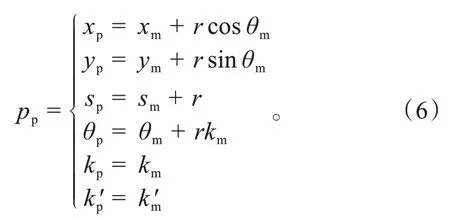
式中：pm为规划起点在指引线上距离最近的点，定义为匹配点，r=(xs-xm)cosθm+(ys-ym)sinθm。

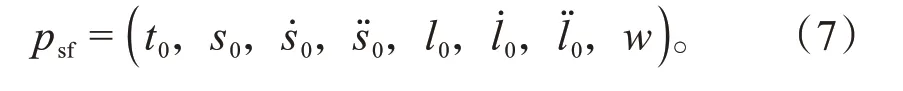
式中：t0，s0，ṡ0，s̈0，l0，l'0，l''0分别为规划起点的时间、行驶里程、纵向速度、纵向加速度、横向偏移、横向偏移速度、横向偏移加速度；w为规划起点是否在指引线所在车道的标志位，规划起点在车道空间为0，否则为与指引路径的距离值。

2.2 横向解空间构造

横向解空间SLM的构造，首先在规划起点psf至最大规划距离ras中利用道路可规划横向区间RE.re.l、RE.re.r建立基本约束；其次将障碍物模型O中静态障碍物及速度小于阈值的动态障碍物转换到Frenet坐标系中收缩横向区间；最后使用自身车辆宽度E.m.d再次收缩横向空间并校验横向空间是否为连通空间，非连通空间则表示无横向规划条件，所以开辟指引线作为连通区域，使横向规划有解。横向解空间构造完成示意图，如图1所示。

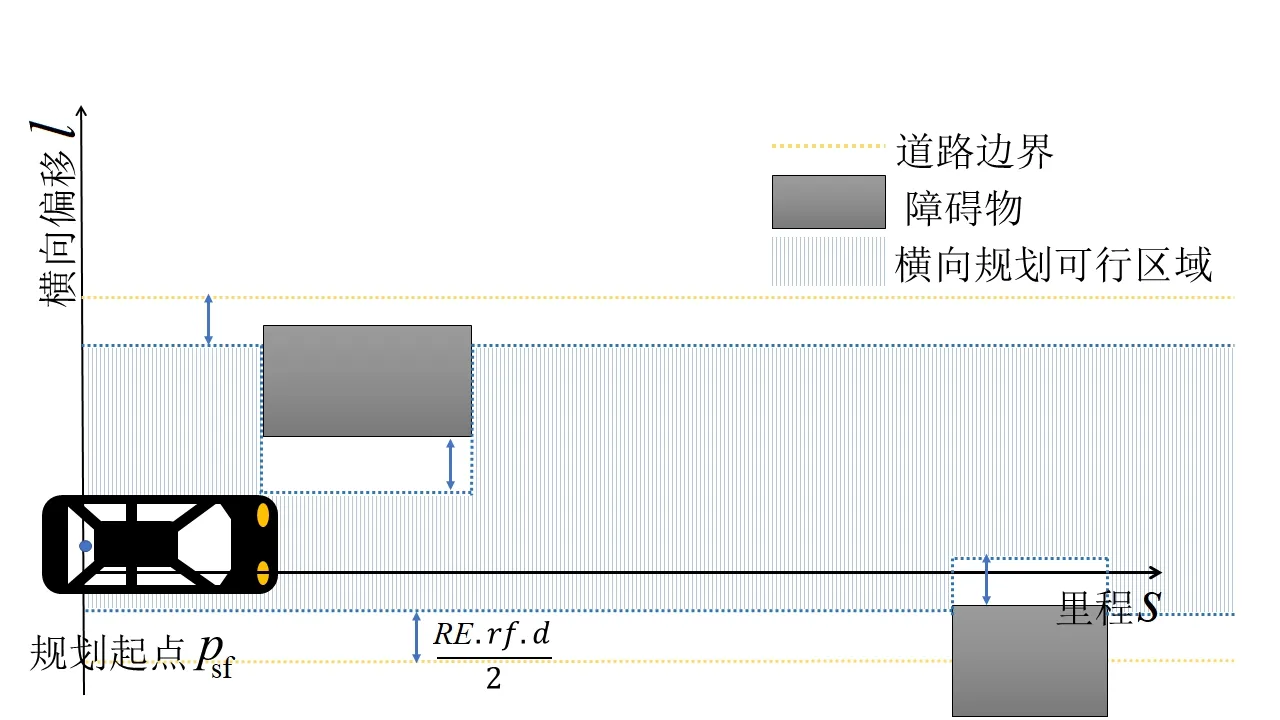
图1 横向解空间构造完成示意图

2.3 纵向解空间构造

纵向解空间STM的构造即是描绘侵占指引线的障碍物，对每一个障碍物在规划时长内以时间为基准进行遍历，并将障碍物转换到Frenet坐标系。在障碍物校验时需要判断障碍物是否处于可规划横向空间，且该障碍物是否超出规划距离。校验通过后以障碍物在Frenet坐标系下所占据横纵向空间的形式输出障碍物数据。纵向解空间构造完成示意图，如图2所示。

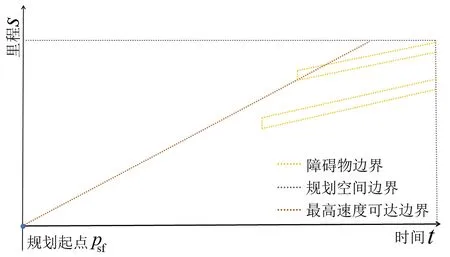
图2 纵向解空间构造完成示意图

由于解耦的固有特性，丢失了一些维度信息，在横、纵向两个解空间中不能完全排除解空间中障碍物所占空间，但此空间已经完全包含可行空间，此问题产生的伪解可以通过碰撞检测排除。

3 横纵向解耦增强混合运动规划方法

3.1 横向偏移混合规划方法

为提高规划效率，在同时满足STM=∅、psf.w=0时，即在解空间不存在障碍物且规划起点在指引线所在车道时，只使用多项式横向偏移规划算法。在不满足上述条件时使用分段jerk横向偏移规划算法进行计算，然后再使用多项式规划算法进行补充。

3.1.1 多项式横向偏移规划算法

首先，以数值方法得到规划终点；其次，对终点与规划起点使用五次多项式规划横向轨迹L(s)。横向规划终点群LP1的定义如式（8）所示。

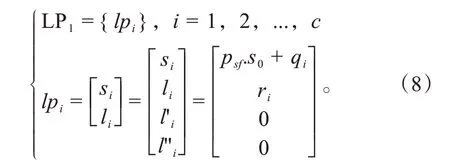
式中：psf.s0为规划起点对应的里程；qi、ri为终点选取参数。

横向偏移规划在规划终点完成横向动作，随后维持l不变，即规划终点l'i=0，l''i=0。车辆处于本车道且前方无任何阻挡，只使用基于多项式规划追踪指引线行驶。本文提出考虑偏差距离取值方法，取0，以确定规划终点。

最后，由规划起点psf和唯一规划终点l p1组成6个横向约束，求解式（9）中多项式表达式系数。解出唯一横向规划解L1(s)，文献［12］中对此方法的完备性进行了详细证明。

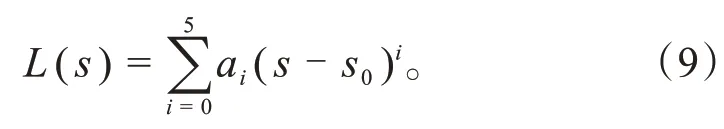
3.1.2 分段jerk横向偏移规划算法

在已经构造的L(s)的解空间SLM中，使用分段jerk法进行横向偏移规划的主要思想，是将车辆横向运动L(s)作为一个3阶系统，构造二次规划问题。

首先建立状态量，从规划起点开始在整个解空间进行规划，离散状态量x为：

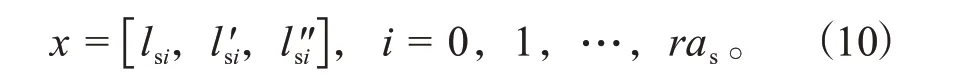
式中：lsi、l'si、l''si分别为指引线离散路径点对应的横向偏移距离、偏移速度、偏移加速度；ras为横向规划距离，综合高速工况要求和计算复杂度，取ras=180。

其次建立约束，具体定义见表1。

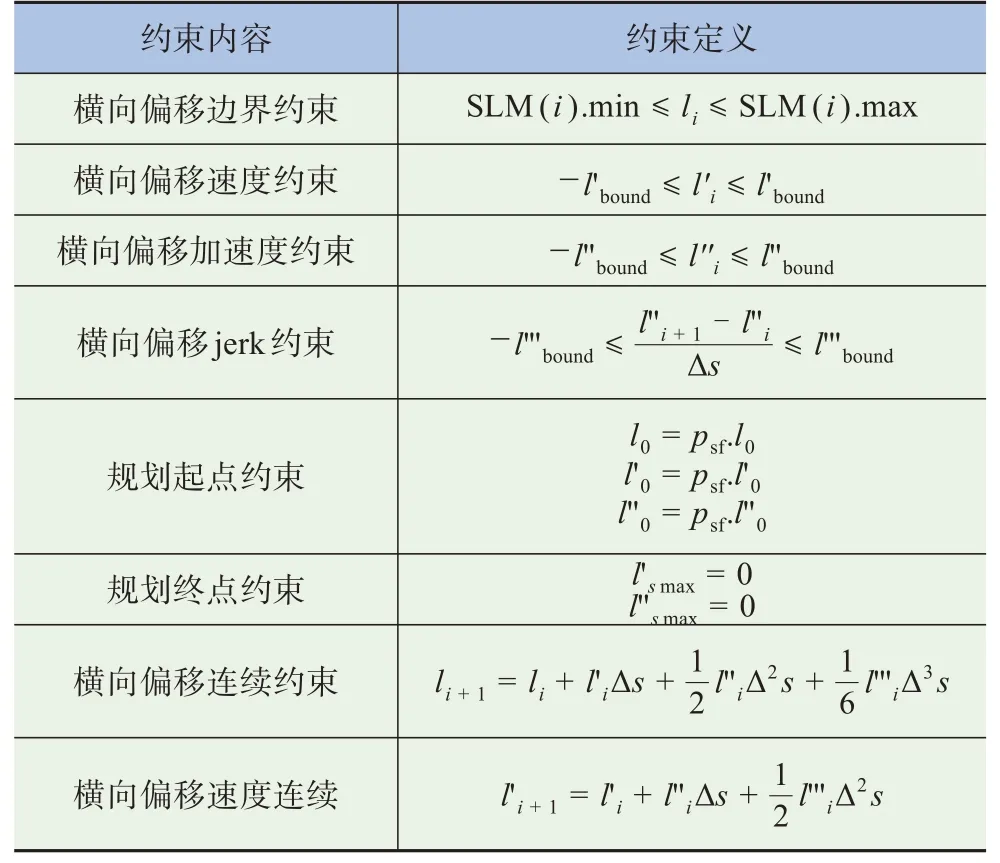
表1 横向规划约束定义

最后构建代价函数，如式（11）所示。

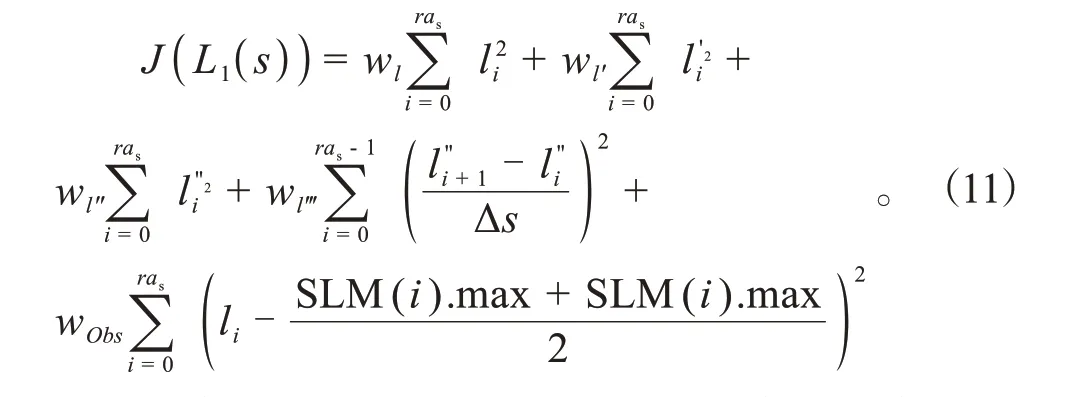
式中：第1项为规划产生的横向偏移代价；第2项、第3项为横向偏移带来的舒适性代价；第4项为结果路径与横向边界的侧向间距所反映的安全冗余。

结合文献和工程实际测试，代价函数权重取值见表2。

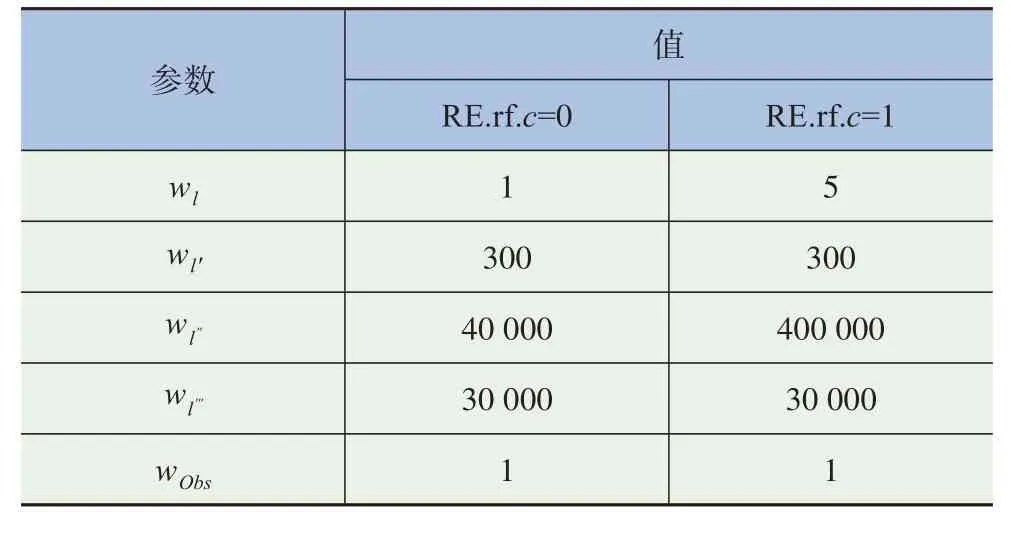
表2 代价函数权重取值

表2中：RE.rf.c为解耦运动规划模型中在指引线范围是否包含了可主动变道工况的标志位。

通过以上步骤完成问题构造，使用osqp求解器［13］解得此解空间内的横向最优解L1(s)，并将其存入横向最优解逼近群LA。

3.1.3 横向偏移规划混合策略

在完成分段jerk横向偏移规划后，使用多项式规划对最优解的合理逼近进行补充，称其为横向偏移规划混合策略，其伪代码见表3。

表3 横向偏移规划混合策略伪代码

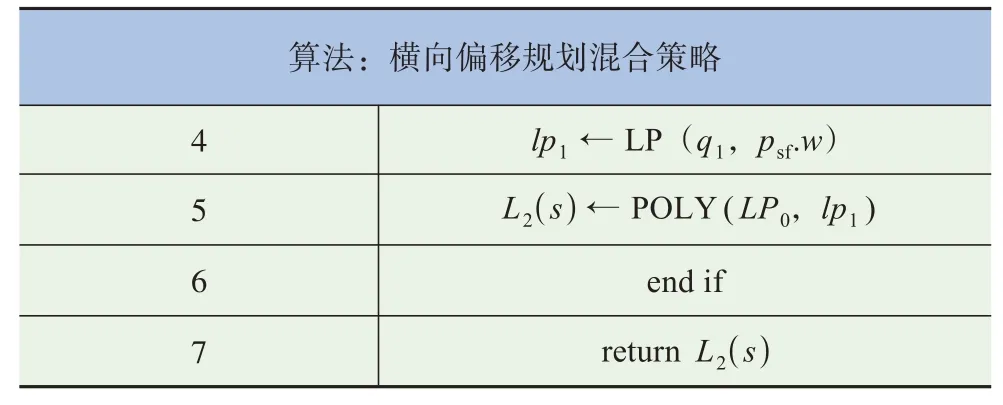
续表

表3中：LP(a，b)、POLY(a，b)函数分别为构造多项式规划约束和使用多项式规划轨迹。混合策略以横向轨迹L1(s)（由分段jerk横向偏移规划算法所生成）中的最大横向变化量∆lmax作为判别依据，使用五次多项式横向偏移规划算法补充一个保持当前车道，依靠纵向速度规划避障的可行横向解L2(s)，将其存入横向最优解逼近群LA。

3.2 围绕不同规划目标的混合纵向规划方法

纵向规划使用多项式规划算法，将围绕速度规划和围绕避障规划两种不同规划目标的规划器进行混合使用，共同解得纵向最优解的逼近群。两种规划器都需要先确定规划终点状态，然后以起始点状态与规划终点状态为约束，使用多项式规划算法解得纵向轨迹S(t)。

3.2.1 围绕速度进行纵向规划

速度规划是纵向规划的本质，在规划终点使车辆达到目标速度，同时在规划终点s''i为0时，才有利于控制纵向规划终点之后的轨迹速度，符合纵向规划系统的物理背景。规划终点群S’P1为：

规划终点状态确定完成之后，利用多项式规划算法求解纵向轨迹，即以规划起点psf和规划终点群S'P1为约束，求解式（13）中多项式表达式系数，可得c∙g个纵向规划结果S(t)。

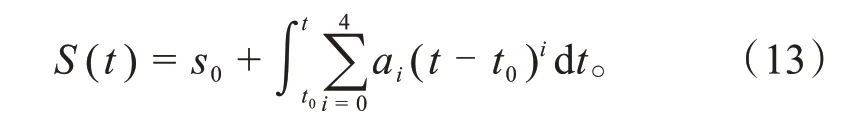
上述方法的完备性、可达性及连续性在文献［9］中进行了详细证明。随后增加一条保持车辆当前速度的纵向规划结果Sn+1(t)=psf.ṡ0，将其作为对围绕速度进行纵向规划的补充，最后将以围绕速度进行规划得到的纵向解存入纵向最优解逼近群LO。

3.2.2 围绕避障进行纵向规划

围绕避障进行纵向规划的目的是跟驰或超越前方车辆。围绕避障的纵向规划方法对纵向解空间STM中的每一个障碍物stm进行处理，规划终点群SP1为：

式中：spij为规划终点群中第i+(c-1)j个规划终点；qi、rij、uij为规划终点选取参数，取值见表4。

表4 围绕避障规划终点取值

表4中：stm.ru.t、stm.lu.t分别为障碍物stm在纵向解空间中所占据的时间最大值、最小值；stm(qi).u、astm(qi).d分别为障碍物stm在qi时刻所占据纵向空间最大、最小值；stm.v为障碍物stm速度。以上数据均为纵向解空间构造时定义并求解完成的数据。d pt为时间规划密度，dpt=2；k、sfi为车距参数，k=2、sf1=5、s f2=10。

规划终点状态确定完成之后，利用多项式规划算法求解纵向轨迹。以规划起点psf和规划终点群SP1为约束，求解式（15）中多项式的表达式系数，可得c∙g个纵向规划结果S(t)。

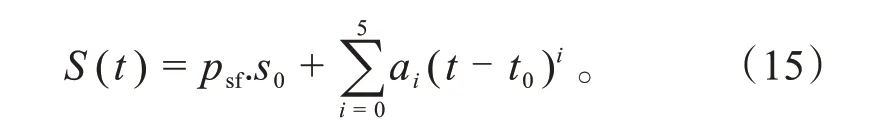
将得到的规划结果存入纵向轨迹最优解逼近群LO，共同构成纵向最优解的合理逼近，其规划如图3所示，黄色标识为障碍物，蓝色线条为纵向规划结果。

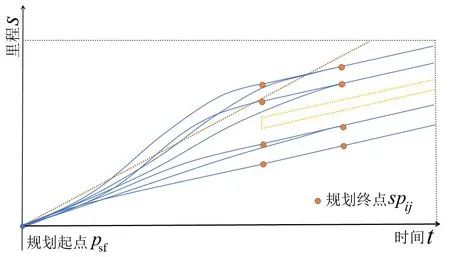
图3 围绕避障进行规划

3.3 轨迹选择

上述过程生成横纵向最优解逼近群之后，需要对其进行组合构成完整轨迹，再在其中选取最优解。

首先，对纵向最优解逼近群LO进行约束校验，将校验所得纵向规划结果和横向最优解逼近群LA中的横向规划结果进行组合，构成完整轨迹群。随后，利用代价函数对所构成的完整轨迹群进行评估，见表5。

表5 轨迹评估代价函数

结合文献和工程实际测试，代价函数参数即权重取值，见表6。表中，RE.rf.d、RE.rf.c为式（1）中的指引线数据。

表6 代价函数参数取值

最后，顺序抽取代价评估后的轨迹，将Frenet坐标系下的轨迹转换到Cartesian坐标系下，并使用最大速度、最大加速度、最大侧向加速度再次进行约束校验。校验通过之后，与道路上的障碍物O做碰撞检测的零一决策，如果轨迹通过校验且无碰撞，则输出轨迹，否则抽取下一轨迹进行校验、检测。

4 仿真验证

4.1 仿真平台搭建

仿真模拟器在无人驾驶算法开发和测试中占据重要地位［14］。本文利用Apollo-LGsvl搭建联合仿真测试平台，以LGsvl模拟器中高速公路高精地图作为道路环境，注入不同静态、动态障碍物，模拟巡航、跟驰、规避静态障碍物、规避动态障碍物等真实交通场景驾驶工况。取巡航车速在80～120 km/h之间，匝道车速为40 km/h。

4.2 规划结果及分析

4.2.1 完成性分析

仿真验证过程中算法执行频率设置为10 Hz，测试巡航、跟驰、避障等工况的最终输出轨迹如图4～6所示。

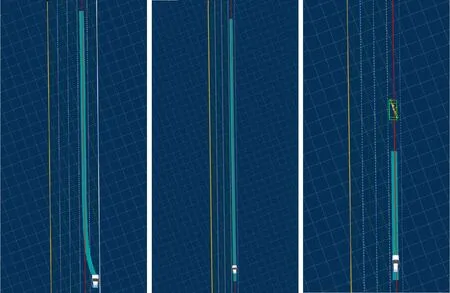
图4 起步、巡航、停车工况仿真结果

图4分别为路边起步、巡航和本车道减速避障工况仿真结果。车辆横向跟踪指引路径，纵向进行速度规划，并由代价函数选择最佳规划结果。

图5分别为自车跟驰所在车道前方不同车辆的工况，车辆横向跟踪指引路径，纵向围绕速度和障碍物进行混合规划以应对具体环境。本文使用的混合纵向规划算法在围绕避障进行规划时会根据他车速度进行速度和距离规划，由代价函数选择最优跟踪轨迹。上述过程仿真中则体现为对他车产生不同速度、不同跟车距离的轨迹。

图5 跟驰工况仿真结果

横向规划空间限制为本车道且存在不完全占据本车道的静态障碍物场景下，横向规划在指引线所提供的可规划空间中生成避障最优路径，如图6所示。在可跨车道避障工况下，用横纵向解耦增强混合运动规划方法进行横向规划时，在变道轨迹基础上补充了一条跟踪指引路径的解，并使用碰撞检测的方式保证最终轨迹的安全性；借道车道存在高速车辆，变道存在碰撞风险时，代价函数与碰撞检测算法选择的依靠速度规划在本车道避障的路径，图6b所示；在无碰撞风险后的借道超车轨迹，如图6c所示。

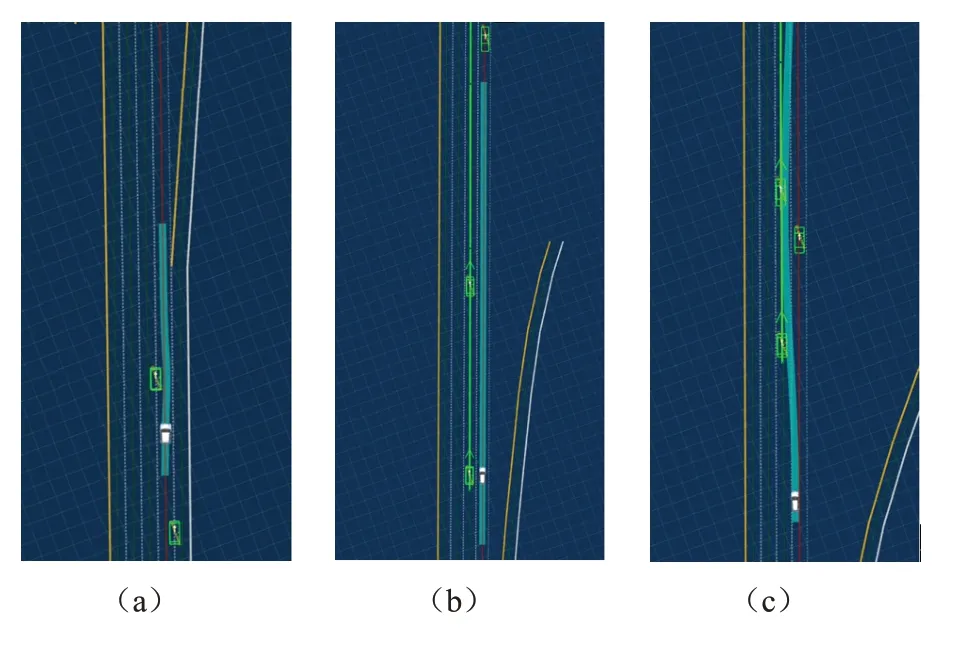
图6 避障工况仿真结果

提取仿真结果中的相关规划结果指标，见表7。各工况中，碰撞次数为0，相关指标均符合动力学约束。综上，本文提出的运动规划方法能够返回一个安全的有效轨迹。

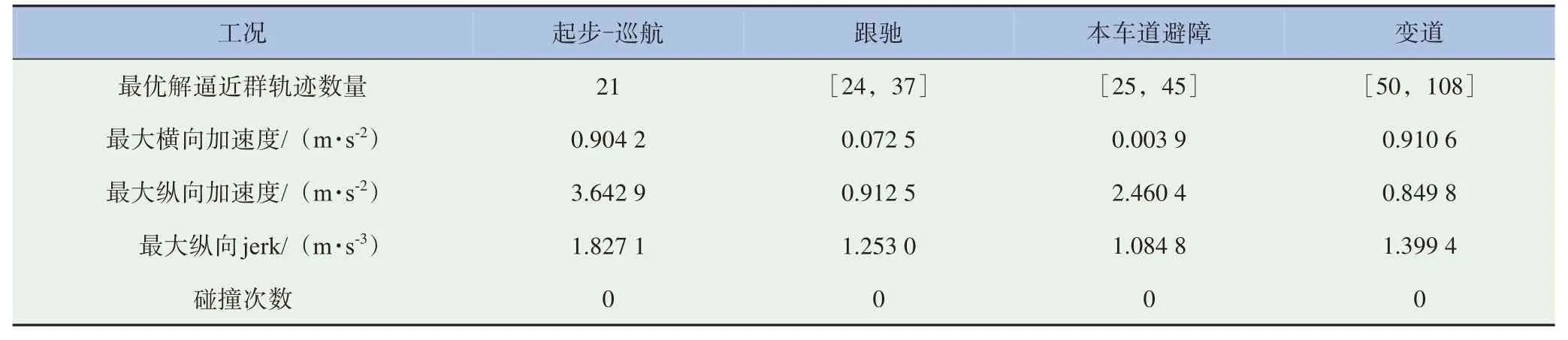
表7 不同工况规划结果指标

4.2.2 结果质量分析

各工况下，规划时间内不同轨迹的航向角θ、转向曲率k和速度v，如图7～12所示。

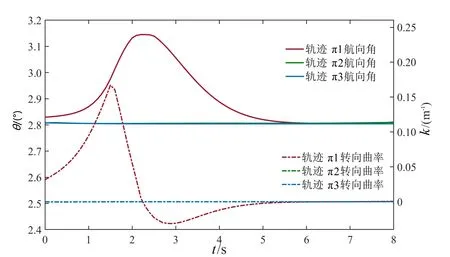
图7 起步、巡航、停车工况轨迹航向角θ、转向曲率k

轨迹π1、π2、π3分别对应图4中的起步、巡航、停车轨迹。起步轨迹π1，航向角θ、参考转向曲率k变化连续平滑，最终与指引线一致，并持续加速。经过渡后生成巡航轨迹π2。避障轨迹π3，在障碍物完全占据车道，不存在通过空间时，车辆横向跟踪指引路径，纵向持续减速，最终停车，速度v变化连续平滑。

轨迹π4、π5、π6分别对应图5中的3种跟驰轨迹，车辆追踪指引路径，纵向速度变化连续平滑，通过规划车速与障碍物保持安全车距。

轨迹π7、π8、π9分别对应图6中的各避障轨迹。轨迹π7对应图6a轨迹，运动规划算法生成航向角和参考曲率变化连续的路径，由于代价函数中的碰撞代价，纵向规划在接近障碍物前将速度降低在安全值内，并且在通过障碍物后重新加速达到巡航速度。轨迹π8、π9分别对应图6b和图6c中的轨迹，轨迹的航向角θ变化连续平滑，参考转向曲率k连续平滑且波动较小，速度变化连续平滑。

综上，不同工况中运动规划产生的轨迹能够保证车辆在进行横向动作时，其航向角θ、参考转向曲率k的变化连续平滑，指引路径本身所具有的曲率变化亦能够在运动规划后保证连续。由于围绕避障进行规划的主要目标是对跟车距离进行约束，所以在部分工况下存在速度有微小超调情况，又由于本文使用多项式进行纵向规划，速度曲线满足高阶平滑，加之轨迹评估选择阶段存在约束校验，所以此项超调可以接受，整体认为速度变化能够保持连续平滑。

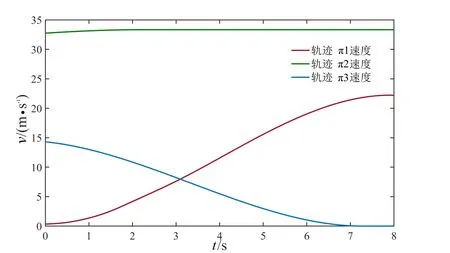
图8 起步、巡航、停车工况轨迹速度v

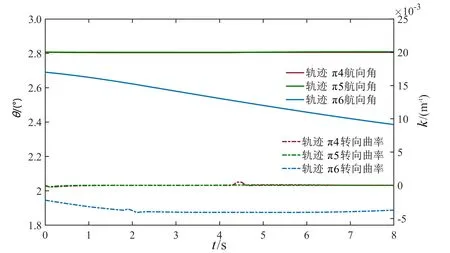
图9 跟驰工况轨迹航向角θ、转向曲率k

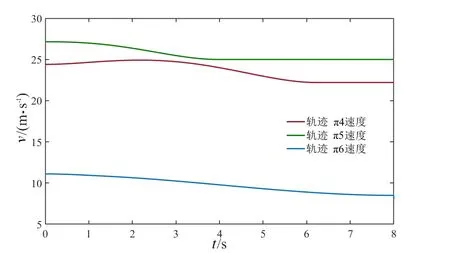
图10 跟驰工况轨迹速度v

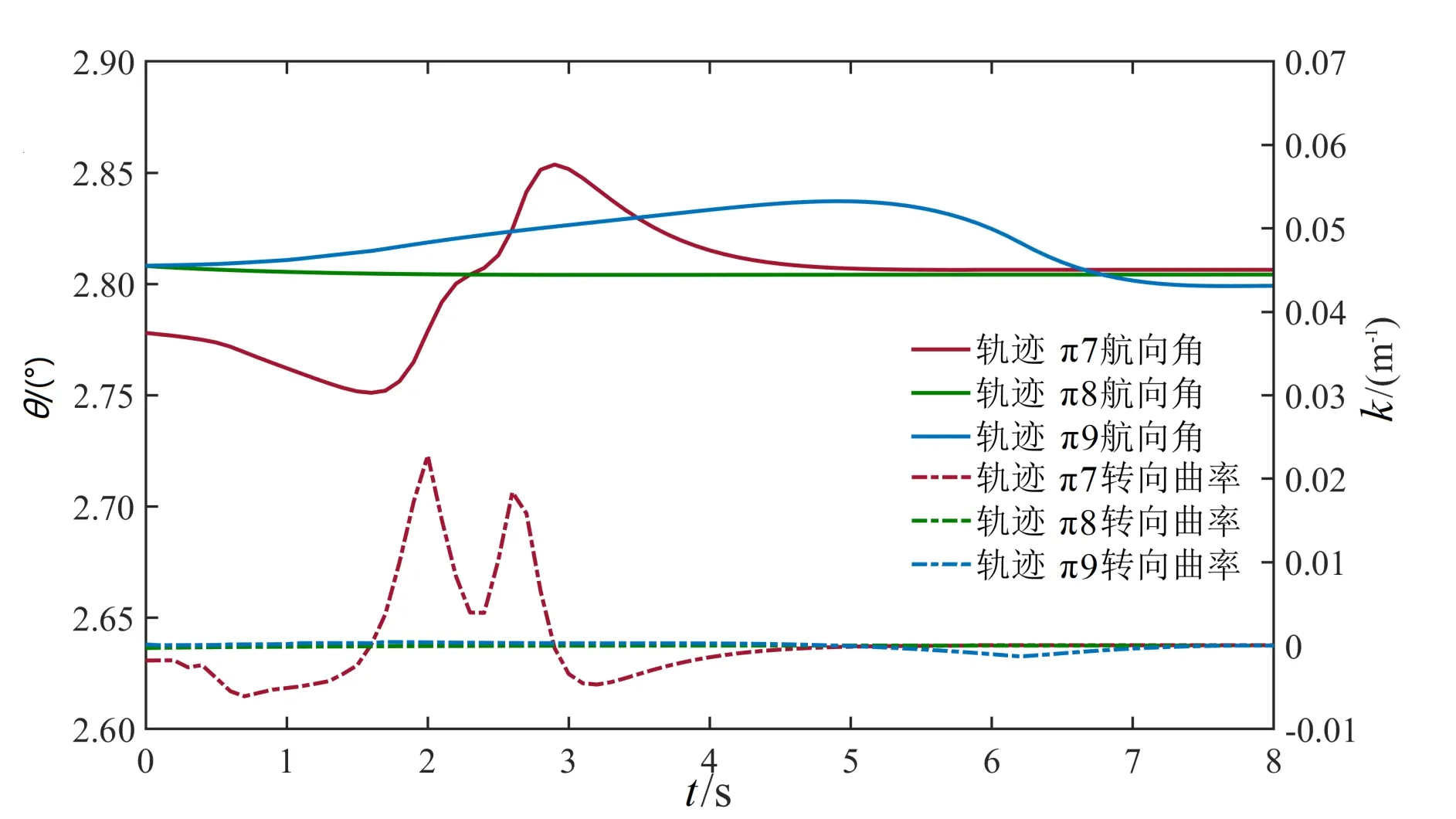
图11 避障工况迹航向角θ、转向曲率k

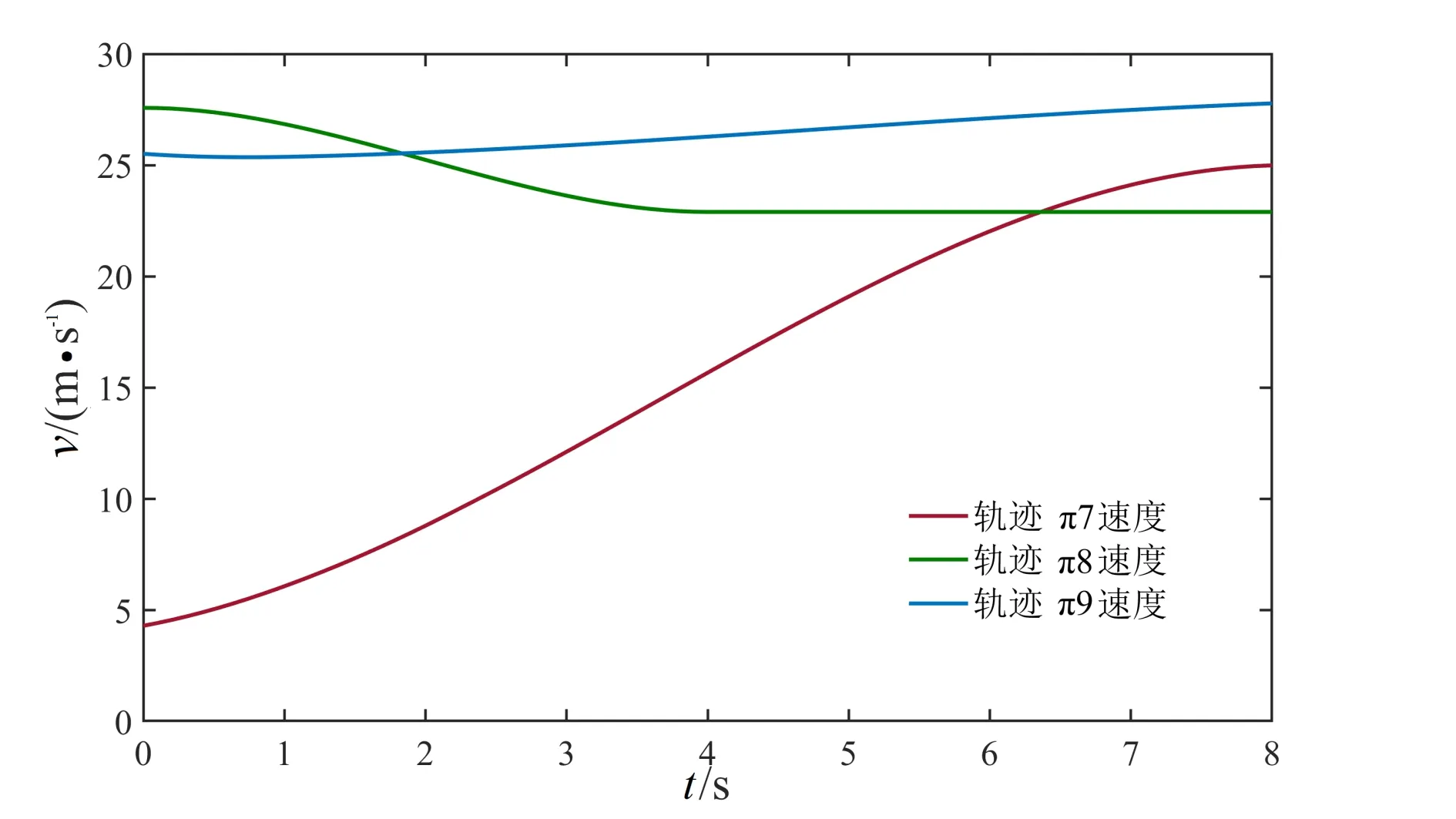
图12 避障工况轨迹速度v

由以上验证结果可知，本文基于OTG所提出的横纵向解耦增强混合运动规划方法实现了在指引线基础上完成运动规划。这种运动规划方法综合了多项式规划算法和分段jerk法的平滑性优势，与其他方法在Apollo-LGsvl平台的对比，见表8，数据表明，算法显著降低了最优解轨迹逼近群中的轨迹数量，使综合工况平均轨迹评估时间缩短为8.625 ms。

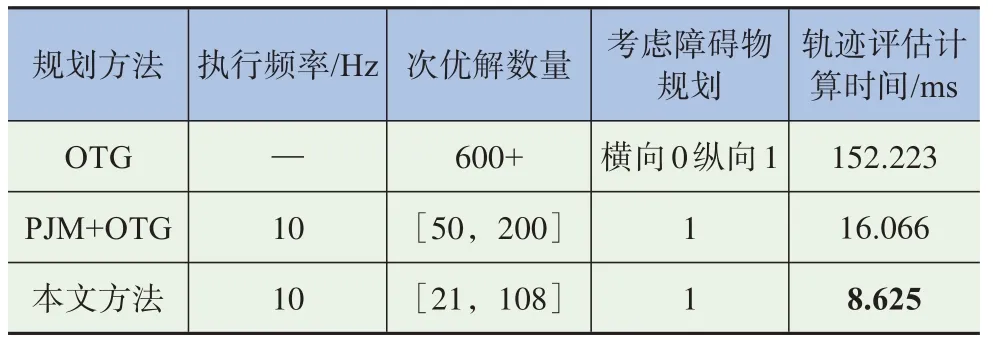
表8 不同运动规划方法在Apollo-LGsvl平台结果对比

5 结论

本文提出了一种横纵向解耦增强混合规划方法，该方法在横向规划中融合了数值优化横向偏移规划算法和多项式横向偏移规划算法的优势，在纵向规划中融合围绕速度和避障进行规划。通过搭建Apollo-LGsvl对所提出的运动规划方法进行仿真验证，主要结果如下：

（1）提出的运动规划方法所得运动轨迹的横向偏移和纵向速度都能满足2阶平滑。

（2）在高速公路各工况中生成的运动轨迹能够有效避免车辆发生碰撞。

（3）所得运动轨迹的最大横向加速度、最大纵向加速度、最大纵向jerk等均满足动力学约束。

（4）有效降低了运动规划算法时间复杂度。综合工况下，相比与分段jerk法混合最优轨迹生成法，本文提出的运动规划方法有效减少了最优解逼近群中的轨迹数量，轨迹评估计算复杂度降低了46%，运动规划算法总时间复杂度降低了15%。

综上所述，本文提出的运动规划方法能够找到一条避免碰撞且满足动力学约束和行驶效率的可行轨迹，同时降低了算法时间复杂度。

横纵向解耦增强混合运动规划算法有以下值得继续优化的方向：针对更复杂、更多交通参与者的环境，对算法中的数据扩展方式做进一步优化；应进一步将障碍物在感知、预测层获取时的延迟及可信度纳入考虑范围，以增强规划安全性和鲁棒性。