基于磁荷观点分析小磁针间的相互作用——以一道竞赛题为例

王 勇

（江苏省常州高级中学，江苏 常州 213000）

电与磁经常联系在一起并相互转化，所以凡是用到电的地方，几乎都有磁过程参与其中.从电磁理论的发展史看，磁理论最初是建立在磁的库仑定律的基础之上，它与电的库仑定律平行，把磁极看成磁荷集聚的地方，将小磁针看作磁偶极子，具有一定的磁偶极矩；后来建立了分子电流理论，将小磁针等价于小螺线管，线圈等价于磁偶极层，电流环有一定的磁矩.前者称为磁荷观点，后者称为分子电流观点.

在第38届全国中学生物理竞赛复赛中第4题涉及到磁体间的相互作用问题，解本题第（2）问与第（3）问关键是必须要求出两个小磁针之间的相互作用势能，而参照2016年版的《全国中学生物理竞赛内容提要》，磁场部分的考试内容只提出了通电圆线圈在轴线上和环面上的磁场和磁矩要求，但相互作用势能并不在竞赛内容要求范围之内.那么小磁针之间的相互作用势能如何理解，相互作用势能表达式怎么推导，小磁针为何等效为无限小圆线圈，如何快速地求出无限小线圈中的电流在轴线上和环面上的磁感应强度，在标准答案之外笔者尝试从磁荷的观点类比电荷间的相互作用分析解决该问题.

例题.一枚小的永磁针可视为一个半径很小的电流环，其磁矩μ的大小为μ＝IS（I为固有不变的环电流强度，S＝πR2，R为电流环的半径），方向与电流环所在的平面垂直，且与电流方向成右手螺旋关系，如图1所示.两枚小磁针A和B的磁矩大小保持不变均为μ，质量均为m.取竖直向下的方向为z轴正方向建立坐标系.将A固定在坐标系的原点O上，其磁矩方向沿x轴正方向；将B置A的正下方.已知真空的磁导率为μ0，重力加速度大小为g.

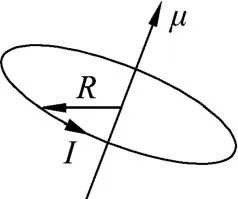
图1

（1）假设B的磁矩方向与x轴成θ角，其质心坐标为（0，0，z）（z≫R），求 A、B之间的相互作用能.

（2）假设z不变，求B可以处于稳定平衡时与x轴所成的角θ稳.

（3）假设z可以变化，但B的磁矩与x轴所成的角θ＝θ稳，求B的受力平衡位置，并说明此平衡位置是否为稳定平衡位置.

1 试题分析

本题研究两小磁针的相互作用，题目中提示将小磁针等效为一个半径很小且磁矩为μ的通电小圆环，通过毕奥-萨伐尔定律积分计算通电小圆环平面内远处的磁感应强度，且用通电小圆环磁矩为μ等效表示出小磁针在远处的磁感应强度，进而计算相距较远的两个小磁针之间的相互作用势能，再通过小磁针之间的相互作用势能分析小磁针的稳定平衡位置.

2 标准解答

计算小磁针A（通电小电流环平面内）在z轴上坐标为z（z≫R）处（记为P点）的磁场，x轴垂直于纸面向外，如图2所示A的电流环（位于yz平面）上Q处电流元为Idl＝IRdφ（cosφj＋sinφk），其中φ为电流元与y轴正方向的夹角，电流元Q到P的矢径为d＝－Rsinφj＋（Rcosφ＋z）k，电流元Q到P的距离

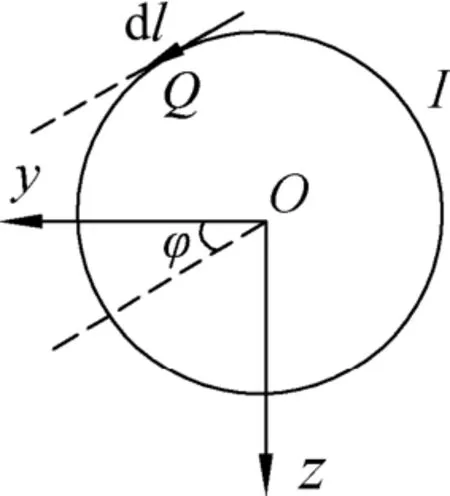
图2

根据毕奥-萨法尔定律有

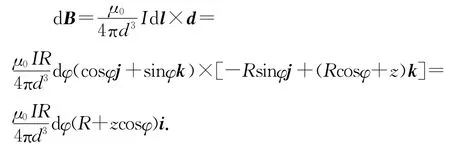
磁感应强度的积分式为

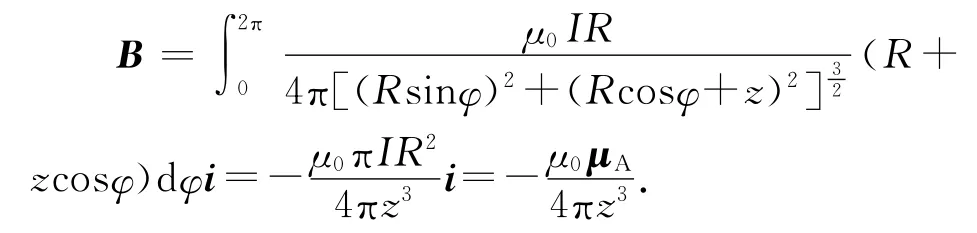
可见A在（0，0，z）处的磁场磁感应强度B沿x轴负方向，取B的磁矩与磁场垂直时为势能零点，则A、B之间的相互作用能为

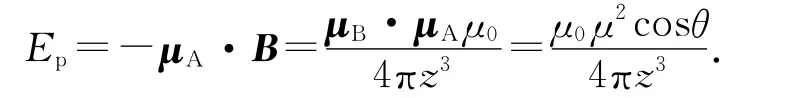
考虑重力后，系统势能为

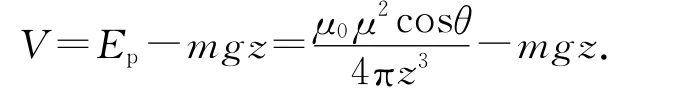
它只与z有关，由于z不变，B受到磁场的外力矩大小为

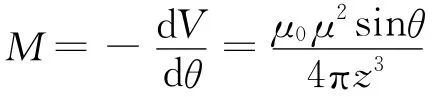
当θ＝0，π时外力矩为0，小磁针处于平衡位置.

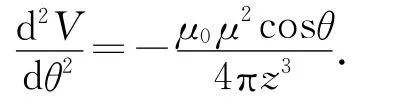
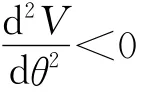
3 磁荷分析法

3.1 小磁针的磁极类比为磁荷

库仑在得到点电荷之间的相互作用力服从平方反比关系后，直觉地感到磁极之间的相互作用力服从类似的关系，若点磁荷1、2的磁荷分别为＋qm1和－qm2，则点磁荷1、2间的作用力为，磁场强度为.

3.2 小磁针类比为磁偶极子

小磁针两端带等量的异种小磁荷，两小磁荷之间的间距极小，小磁针可看成一个磁偶极子.设小磁针的N极带正磁荷＋qm，小磁针的S极带负磁荷和－qm，两磁荷间的距离为l，磁偶极距为pm＝qml，方向由负磁荷指向正磁荷.

3.3 磁偶极子类比为电偶极子

相距较近的等量的异种电荷构成一电偶极子，若电偶极子的极距为pe，则电偶极子在延长线和中垂线上的电场强度分别为

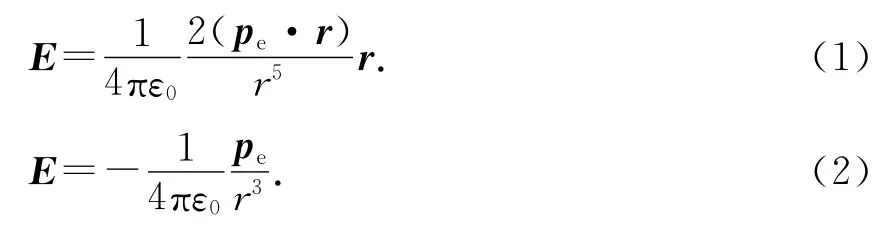
电偶极子在电场强度为E的匀强电场中的力矩为

电偶极子在电场强度为E的匀强电场中的电势能为

类比电偶极子的（1）、（2）式则磁偶极子在延长线和中垂线上的磁场强度分别为

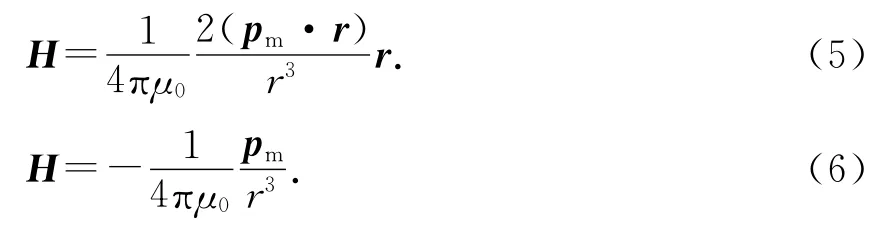
类比电偶极子的（3）式则磁偶极子在磁场中的力矩为

类比电偶极子的（4）式则磁场强度为H的匀强磁场相互作用的电势能为

3.4 小磁针类比为通电小圆环分析小磁针在磁场中的相互作用势能

磁矩为μ的通电小圆环在磁感应强度为B的匀强磁场中力矩为

由于在真空中

比较磁偶极子在磁场中的力矩（3）式和（10）式与通电小圆环在磁场中的力矩（9）式则小磁针的磁偶极矩为

将（10）式和（11）式代入（8）式，则有小磁针在磁场中的相互作用势能为

通电小圆环平面内远处的磁场等效为磁偶极子中垂线远处的磁场，磁偶极子中垂线远处的磁场可类比为电偶极子在中垂线上远处的电场，则小磁针中垂线上（或通电小圆环平面内）远处的磁场强度表达式为（6）式.将磁偶极矩（11）式代入（6）式后可得磁场强度为

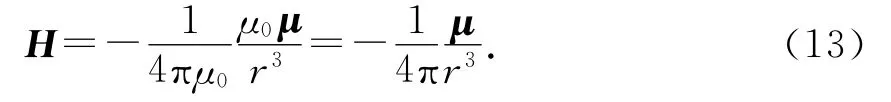
当两小磁针中心距离为z（z≫R）时，（0，0，z）处小磁针的磁感应强度为

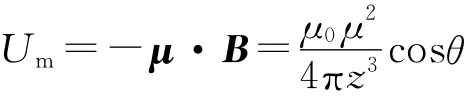
比较上述两种解法，磁荷观点简便很多，磁场相关概念与静电场的规律一一对应，有关静电场的概念、规律、定理、讨论方式以及计算结果等几乎都可以直接借用.将小磁针类比为电偶极子从磁荷的角度解决相关磁场问题是一种有效的方法，也便于深入理解磁场的相关概念规律.