非相对论近似下的磁矩算符及应用
万 猛,高钦翔,杨友昌,潘正坤
(遵义师范学院物理系,贵州遵义563002)
非相对论近似下的磁矩算符及应用
万 猛,高钦翔,杨友昌,潘正坤
(遵义师范学院物理系,贵州遵义563002)
从夸克流出发,在非相对论近似下推导得出了磁矩算符的具体形式;并以质子磁矩为例,讨论了重子磁矩的计算。
磁矩算符;重子磁矩;狄拉克流;轨道角动量
强子结构一直是强子物理研究的基本课题,也是物质微观结构研究的前沿和热点问题。1964年Gell-Mann提出的强子结构模型—分数夸克模型[1],认为SU(3)群的基础表示对应着三种粒子,即u,d,s三种夸克,具有分数电荷。夸克模型成功地解释了由u,d,s三种夸克组成的处于空间轨道基态,符合味道SU(3)对称的自旋为1/2的八重态重子和十重态重子的许多性质,尤其是预言了由3个奇异夸克组成的Ω重子的存在和质量,并被后来的实验所证实。夸克模型令人印象深刻的成功之一是仅用两个组分夸克质量参数,就成功地解释了观察到的所有重子的磁矩,即:
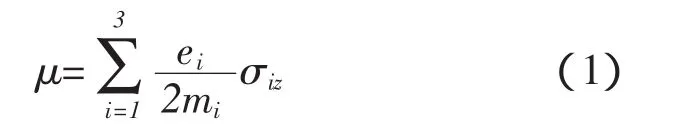
式中e、m和σ分别为电荷算符,质量算符和泡利算符,求和表示对重子中所有的组分夸克进行作用。一般情况下,重子磁矩[2]除自旋角动量的贡献外,还应包含轨道角动量的贡献,即

对于基态重子,3个组分夸克都处于轨道L=0的S态,因此轨道角动量对磁矩的贡献为0,所以只考虑自旋角动量对磁矩的贡献,即(1)式。
本文从狄拉克流出发推导非相对论近似下的磁矩算符,并简要说明重子磁矩的计算。
1 基本思想
1.1 狄拉克流
量子场论中的狄拉克流为

(2)式中γμ称为狄拉克矩阵(μ=0,1,2,3):
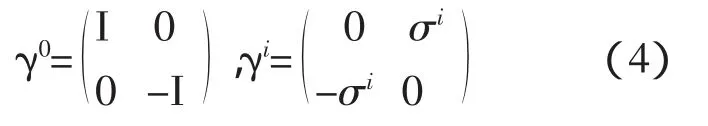
其中i=1,2,3,I是2×2的单位矩阵,σi是2×2的泡利矩阵:
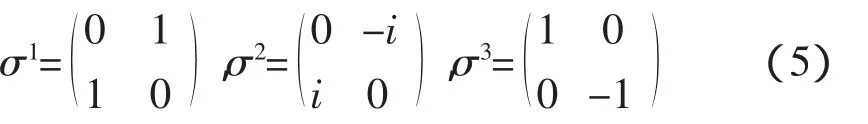

其中u,v是与时空坐标无关的四分量旋量,称为狄拉克旋量。a+,b+和a,b是粒子产生和湮灭算符。
一个电子和正电子组成的体系的电磁流密度四矢量jμ(x)代表了电荷或流的分布,其形式为,

1.2 磁矩算符
狄拉克理论中电子的磁矩由下式给出

考虑单电子态,即具有确定的动量,在t=0时,

因此有
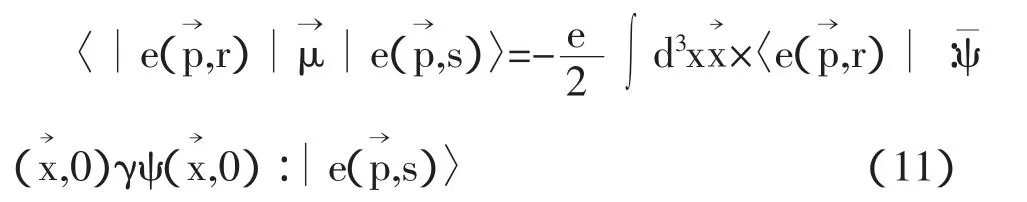
将(5)式代入上式有
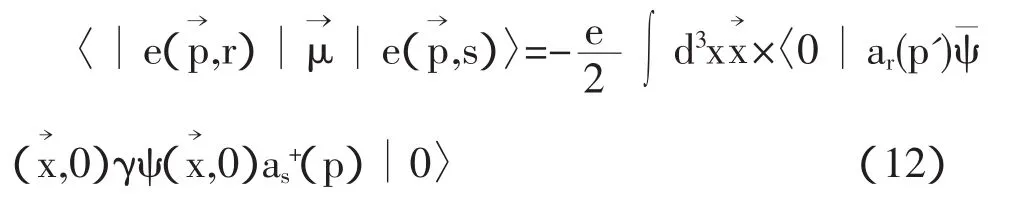
式中
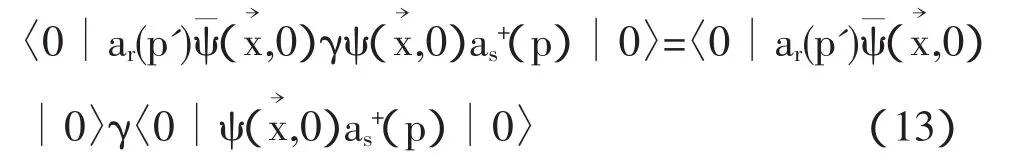
其中
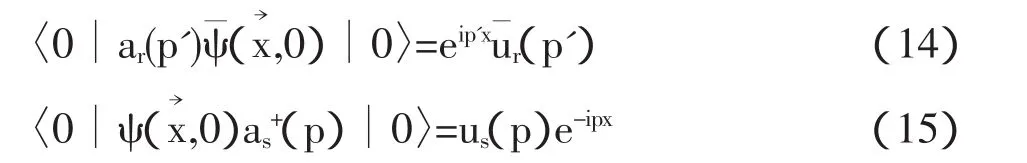
则

在非相对论近似下,|p|< 因此 利用公式, 为了让表达式的形式更为清楚,利用归一化的单电子态 在非相对论近似下,函数满足以下条件: 且 通过计算可得 即 因此,非相对论近似下的磁矩算符为 根据(30)式,可得出计算重子磁矩的表达式为 重子波函数包含色、味、自旋和轨道4个部分,如质子的波函数为 式中[21]f,[21]s,[3]x,[111]c利用了群表示理论中的配分表示,分别代表味、自旋、轨道和色空间的波函数及相应的对称性。质子波函数中味和自旋部分的具体形式为, 由于在3夸克体系中,轨道角动量对磁矩没有贡献,因此磁矩算符只对味和自旋部分的波函数有作用。将质子自旋和味函数(34)代入(32)式,可得质子磁矩, 根据式(30)-(32)式知,对于角动量不为零的强子态,除了考虑自旋对磁矩的贡献外,还应考虑轨道部分的贡献。近几年对重子的实验研究数据表明:重子中可能存在5夸克成份的迹象。由于基态重子的P宇称为正,如果考虑5夸克成份,则5夸克系统内部必有一个P波存在。考虑轨道部份对磁矩的贡献,文献[2]-[5]对质子的磁矩进行了讨论。 综上所述,从狄拉克流出发,详细讨论和推导了非相对论近似下的磁矩算符。该算符可以应用于所有强子态的磁矩计算。本文以质子磁矩的计算为例,讨论了该算符在重子和奇特重子态中的应用。结合最新的实验数据,我们将对重子磁矩进行更为系统的理论研究。 [1]Gell-Mann M.A Schematic Model of Baryons and Mesons[J].Phys.Lett.1964,(8):214-215. [2]Chen Hong.Spin Structure of Baryons in Orbiting Valence Quark[J].Commun.Theor.Phys.1998,(29):425-430. [3]Zou B S,Riska DO.The component of the proton and the strangeness magnetic moment[J].Phys.Rev.Lett,2005,95,(7):1-4. [4]An C S,Riska D O,Zou B S.The components and hidden flavor contributions to the baryon magnetic moments[J].Phys.Rev.C,2006,73,(3):1-7. [5]An C S,Li Q B,Riska D O,Zou B S.Strangeness spin, magnetic moment and strangeness configurations of the proton[J].Phys.Rev.C,2006,74,(5):1-8. (责任编辑:朱 彬) Magnetic Moments Operator and its Application in Non-relativistic Approximation WAN Meng,GAO Qin-xiang,YANG You-chang,PAN Zheng-kun Based on the quark current,the magnetic moments operator is obtained in non-relativistic approximation.Taking the proton moments as an example,we discuss the calculation of baryon moments in this work. magnetic moments operator;baryon magnetic moments;Dirac current;orbital angular momentum O413.3 A 1009-3583(2010)-03-0068-03 2010-01-12 贵州省教育厅自然科学类资助项目(黔教科20090054);遵义师范学院重点学科建设项目(理论物理)(院科字185(11)号) 万猛,男(仡佬族),贵州遵义人,遵义师范学院物理系讲师,硕士。
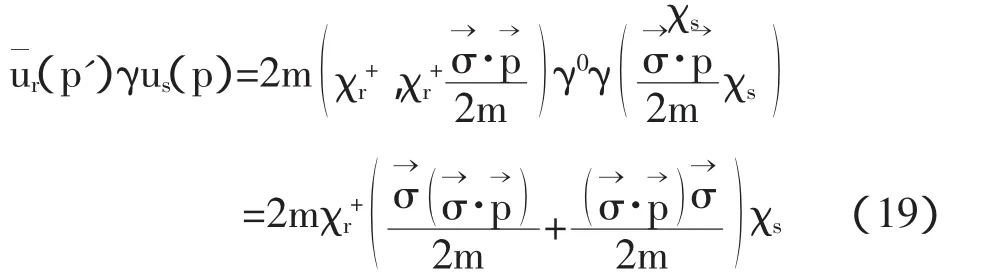
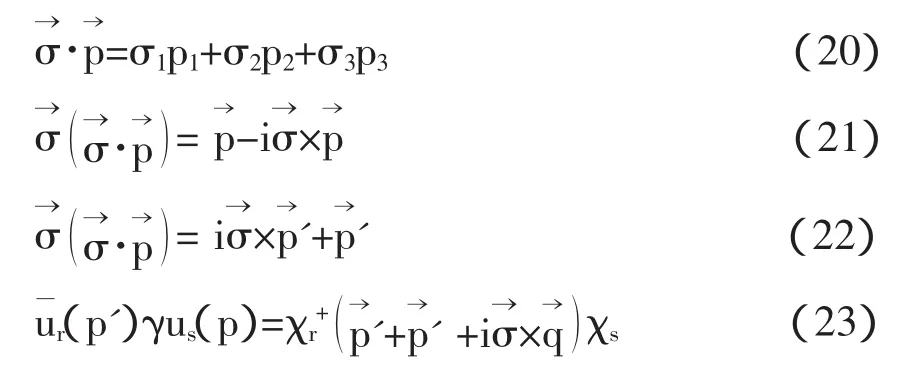
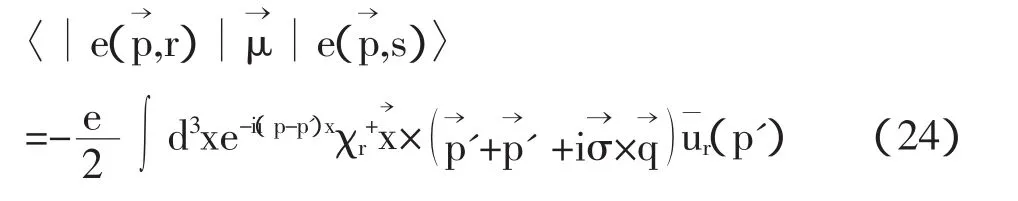

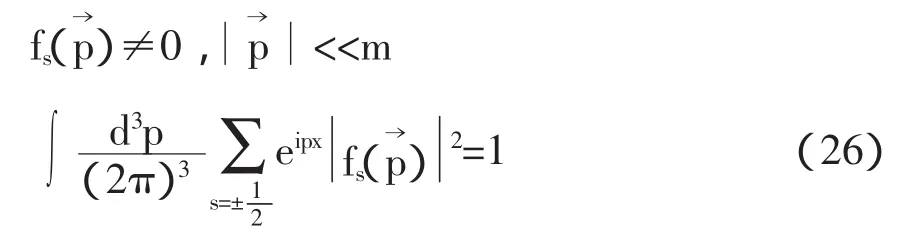
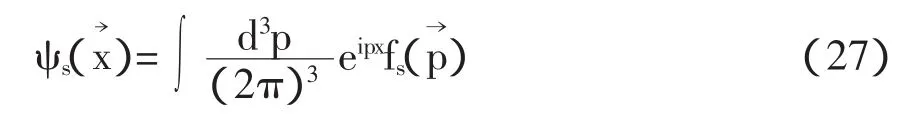
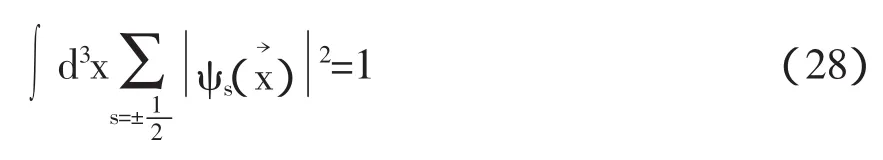
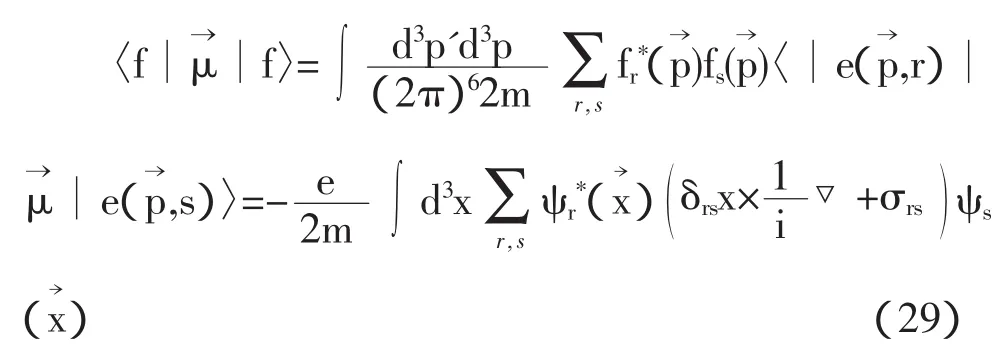
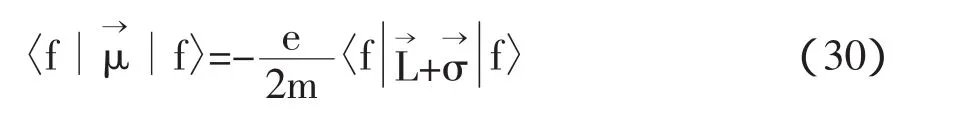

2 质子磁矩的计算
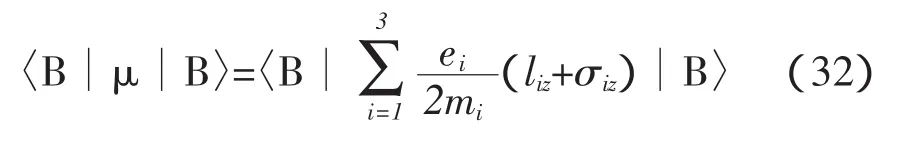
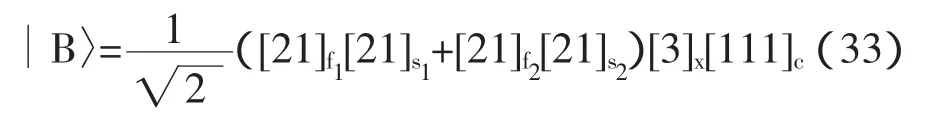

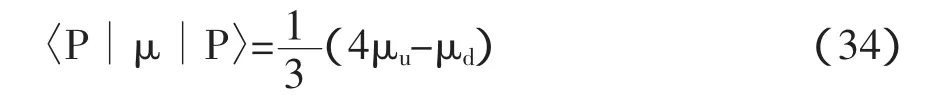
3 小结
(Department of Physics,Zunyi Normal College,Zunyi 563002,China)

