工作记忆中“组块”概念的演化及理论模型
陈玉田 陈 睿 李 鹏
工作记忆中“组块”概念的演化及理论模型
陈玉田 陈 睿 李 鹏
(云南师范大学教育学部, 昆明 650500)
在Miller提出“神奇的数字7±2”之后, “块”被很多理论作为个体工作记忆加工过程中具有稳定结构并可用于衡量记忆容量的单位。但随着研究者对“组块”研究的深入, 他们对组块的定义也在发生着改变。与此同时, 不少研究发现个体的年龄阶段与其主要采用的组块层级相对应, 但尚不清楚组块层级的转换是否存在固定的年龄区间, 且对组块机制的解释仍存在分歧。因此本文针对组块定义的发展与演变、年龄阶段特征及其机制三方面展开综合讨论。未来的研究可以更多探讨长时记忆在工作记忆组块运行机制中的作用, 完善不同年龄阶段个体的组块特征, 以及怎样发挥复述策略和“少即是多”原则在组块过程中的优势等问题。
组块, 工作记忆, 模型结构, 容量
1 引言
在日常生活中, 当你需要在短时间内识记大量信息(如, 电话号码)时, 你会采用什么策略?对信息进行组块(chunking)也许是一个不错的策略选择。研究表明, 在人际交往的过程中, 人们可以通过人际关系对人群进行组块以增加工作记忆容量, 从而提高识别社会群体的能力(Stahl & Feigenson, 2014)。在学习外语的过程中, 组块可以提高单词以及语法学习的效率(Alluhaybi & Witzel, 2020)。因此, 对组块机制的研究有助于探索更好地存储与提取信息的方法。有研究指出, 由于工作记忆受到容量限制, 人们倾向于将重复出现或者具有相互关联的信息, 通过重新编码组织成块(chunk)信息, 以扩展存储容量(Chekaf et al., 2016), 换言之, 就是将信息进行组块。关于组块的研究最早起源于短时记忆, 该研究指出组块的主要功能是对信息进行存储(Miller, 1956)。然而, 另有研究则认为相对于短时记忆, 工作记忆中的组块不仅具有存储信息的功能, 还包括对信息进行暂时加工的功能(Cowan, 2019)。因此, 对工作记忆的研究也必然涉及对信息进行组块的过程。已有研究以国际象棋棋手为研究对象发现, 专家与新手的区别在于, 专家之所以比新手能记住更多的棋子布局, 原因在于专家可以运用更加丰富的经验形成更多的棋子组合(Sala & Gobet, 2017)。这表明对信息进行组块存储可以提高个体加工的效率。另外, 在认知心理学研究中, 组块程度成为衡量个体加工复杂任务时的工作记忆能力标准之一(Sala et al., 2017)。
2 组块定义及其演化
James (1891)在记忆容量的研究中发现, 将存在时间关联性的事物进行串联可以提高个体的记忆容量和效率, 该研究可以被认为是对组块雏形的描述。此后, 组块开始进入研究者视野。然而, 国内的一些研究对组块一词的使用存在概念上的混淆, 组块既用于表达对信息的整合过程, 也用于表达信息整合的结果。通过对文献的梳理发现, 块(chunk)所强调的是将信息整合的结果, 组块(chunking)则强调将零散的信息按某一特征进行划分的过程(Gobet et al., 2001; 彭聃龄, 2019), 二者的共同目标均为提升记忆的能力, 本文拟着重探讨组块这一概念。组块的定义在不断发生着演变, 究其原因, 可能在于不同研究者对个体信息组块过程的认识不同。总结前人研究发现, 个体主要以对信息进行策略化重组和寻找共同特征两种方式对信息进行组块。
基于策略化重组这一方式, 源于Miller (1956)提出的组块是指个体在面对复杂记忆任务时, 根据语义之间的联系将碎片信息进行整合以便提高记忆容量的过程。当语义信息不断输入时, 个体就会对信息进行有组织的叠加, 每一次信息叠加形成的块都比旧有块包含更多信息, Miller将这一过程称为信息的重新编码。此后, 基于Miller的概念, Baddeley (2003)指出, 工作记忆作为一个独立的记忆系统, 其中所包含的情境缓冲器(episodic buffer)作为临时存储系统将信息捆绑后整合成情境(episodes), 组块则是对旧信息的激活, 同时在工作记忆的操作下对原有信息进行改造。另有研究也证明, 不同记忆系统中相关联信息的重新编码对组块具有重要影响(Atkinson & Shiffrin, 1968; Malmberg et al., 2019)。上述定义着重强调了个体在对识记信息进行组块时是对重组策略的激活和使用。
基于寻找共同特征这一方式, Cowan (2001)认为, 信息重组策略虽然可以不断提升块容量, 但同时也会对计算工作记忆的纯粹容量产生干扰, 组块应是个体将不同信息的共同特征相互关联的过程。随后, Gobet等人(2001)进一步强调了信息之间共同特征的多少是组块的关键。
此外, 随着组块概念的不断演化, 其所包含的层级结构也发生变化, 并与不同年龄阶段形成对应关系。
3 组块的层级结构与年龄发展特征
影响信息组块的因素包括信息之间的关联程度(包括外部联系和内部联系)、语义知识以及过去经验, 上述因素在信息组块中的共同作用在于对信息的压缩, 不同点则在于对信息压缩的程度以及方式存在差异。当个体依据信息之间的关联程度对信息组块时, 最主要的方式在于寻找信息之间的规律, 对信息的压缩并不会改变信息的原貌(例如: 个体在记忆a a a b b b c c c这9个字母块时, 会依据字母外型将其分为“a a a”, “b b b”, “c c c”三个块。再例如: 个体在记忆轮船、汽车、香蕉、苹果这个4个词块时, 会依据内在属性将其分为“轮船、汽车”, “香蕉、苹果”两个块)。当个体依据语义知识和过去经验对信息进行组块时则会对信息进行重新编码压缩, 改变信息原有形态(例如: 在面对1 9 4 9四个数字块时, 个体会将其编码为“新中国成立时间”一个块) (Chekaf et al., 2016)。与此同时, 影响信息组块的因素也导致块具有不同的层级结构。
前人对块的类型进行了诸多叙述, 例如有研究者表示块可以分为以下3种类型: (1)对外型以及性质完全一致的事物进行分组后形成的块; (2)对外型不一致但具有内在关联性的事物进行分组后形成的块; (3)根据现有信息再利用过去经验进行重新整合后形成的块(Mclean & Gregg, 1967)。另有研究者则认为块的类型分为: (1)单个事物独立形成的块; (2)单个事物互相组合形成的块; (3)多个块相互镶嵌形成的超级块(super chunks) (Rosenberg & Feigenson, 2013)。研究认为, Mclean所划分的前两种类型的块在形成过程中并没有质的区别, 应该被划分为同一层级两种不同类型的块。因此可依据前人对块的分类以及块的复杂程度将块分为3个层级: (1)单个且互不相关的事物独立形成的块; (2)依据事物外部或内部特征的联系进行分类后形成的块; (3)根据语义知识和过去经验将事物重新编码形成的超级块。对以往的文献梳理后发现, 块的层级结构与个体的年龄、认知的发展有着密不可分的关系。黄福荣等人(2017)提出, 个体对外部事物的表征存在一个基础的认知体系, 认知体系的发展影响着个体组块功能的发展程度。
研究认为, 处于14个月之前婴儿期的个体更多表现出第一层级的组块特征, 该时期的婴儿只能识别单个物体, 不能依据单个事物之间的外部或内部联系对事物进行组块。Kingo和Krøjgaard (2012)通过手动搜索任务范式, 首先给10至12个月的婴儿展示1个球后, 将其隐藏在盒子里让婴儿搜寻, 之后又给婴儿同时展示4个相同的球后再次让婴儿搜寻。两次搜寻的结果表明, 婴儿每次只能搜寻出1个球, 且搜寻时间大致相同(Wang & Feigenson, 2019), 以此证明儿童不能将4个相同的球进行组块后记忆。这一结果得到了对6至7个月(Kibbe & Leslie, 2019)、10至12个月(Applin & Kibbe, 2021)或12至14个月(Stahl & Feigenson, 2018)婴儿被试的研究证据支持。导致婴儿无法将多个球进行组块的原因可能在于, 婴儿对单复数概念存在理解限制(Peng et al., 2018)。
当婴儿成长到14个月以后, 随着语言能力的快速发展, 他们逐步能形成具有第二层级特征的块。但由于该阶段婴儿的个体差异较大, 因此, 现有研究对婴儿何时能形成稳定的第二层级特征块并未达成一致, 但基本确定其年龄范围大致为14至22个月。以往研究存在两种观点, 一种观点认为婴儿组块从第一层级到第二层级的转折发生在14个月左右。研究发现, 从第14个月开始婴儿已经意识到事物之间存在相似特征, 但对事物进行组块的能力尚不稳定, 还需要成人的协助(Stahl & Feigenson, 2018)。另一种观点则认为转折期发生在第22个月左右, 并从以下两个方面对其进行论证: (1)从脑机制发展角度来看, 个体的外侧前额叶皮层和腹侧颞叶区对物体的识别及对工作记忆的存储有重要影响, 婴儿在22个月以后的发育才相对成熟(Guida et al., 2020)。此后, 婴儿开始由只对单个物体特征的识别转向对多个事物共同特征的识别, 为其具备第二层级组块的能力奠定了生理基础; (2)从婴儿语言发展角度来看, 婴儿在22个月左右可以掌握单复数概念, 使婴儿对单个事物和多个事物的区别在概念上有了认知(Peng et al., 2018)。22个月以后婴儿开始能进行第二层级的组块, 即可以独立抽取事物之间相同特征进行组块。但此时的婴儿缺乏知识和经验, 较难触及事物共有属性, 只能依赖感知觉对事物进行组块记忆(Forsberg et al., 2021; Smalle et al., 2015)。
进入成年期后, 由于语义和过去经验发展迅速, 个体开始掌握第三层级特征的组块。Feigenson等人(2013)研究发现, 相比婴幼儿成年人更容易根据语义和过去经验形成超级块。例如, 马拉松运动员可以将5 1 2 4这4个数字重新编码为“5小时12分4秒”进行记忆。在成人的组块研究中, Ding等人(2017)在交互式动作、单独动作、非交互式动作的记忆研究中发现, 对彼此具有联系和交互式意义的动作记忆过程中, 被试会调取来自长时记忆的语义知识对动作进行组块记忆。在字母记忆的研究中发现, 与对数字进行编码记忆相同, 成年被试同样可以将不同的字母进行重新编码后记忆(Stahl & Feigenson, 2018)。例如, 在记忆字母B B C N B A时, 可以通过单词缩写词BBC NBA对字母赋予意义后进行记忆。对专家在国际象棋棋盘布局的记忆研究中发现, 棋手会依据棋子位置联系, 将其重新整合并编码成超级块, 同时赋予语言标签后存储在长时记忆中, 方便快速提取(Kibbe & Feigenson, 2014)。总结上述研究可得出, 在对语言概念的熟练掌握下, 成人逐渐掌握事物共同的抽象属性, 并以此进行组块。
通过文献梳理可看出, 当前研究更多集中于对婴儿期和成年期个体的研究, 对儿童期和青少年期个体的组块研究较少, 因此, 尚无证据表明组块从第二层级到第三层级的转折发生在何时, 未来研究可以更多地对这两个年龄阶段个体的组块特征进行研究。
4 组块的理论模型
4.1 组块理论(Chunking theory)
Chase和Simon (1973)在Miller理论的基础上更系统地提出了组块理论, 并基于“基本知觉和记忆模型” (Elementary Perceiver and Memorizer, EPAM)计算机程序提出假设: 学习的发展和短时记忆的存储是通过鉴别网络中节点(node)的相互联系发生的。EPAM是一个模拟对不同外部刺激的相互联系进行分层鉴别网络模型, 从上往下依次由多个具有辨别功能的节点和连接不同节点的线段构成, 个体可以通过网络将不同类型的刺激进行分类形成新的块进行存储(Gobet, 2005)。此后, Simon和Barenfeld (1969)进一步将用于收集棋手眼动数据的PERCEIVER程序与EPAM连结, 从而提出“记忆辅助模式感知模型” (Memory-aided Pattern Perceiver—MAPP)。该模型包含学习组件和性能组件两个部分。其中学习组件(learning component)使用EPAM的辨别网络学习机制, 用于模拟长时记忆对不同棋子布局的存储模式; 性能组件(performance component)包含3个运行步骤: (1)检测显著的棋子布局; (2)识别存储于长时记忆中来自学习组件的棋子布局, 并且将其调取到短时记忆中进行临时存储; (3)重新编码存储于短时记忆中的棋子布局, 并覆盖旧有布局, 以此进行位置学习, 扩充块的规模(Pförtner & Hristova, 2021) (MAPP流程详见图1)。例如, 当个体在识记B B C F B I这6个字母块时, 学习组件会运用长时记忆中所保存的过去经验将6个字母依次编码为“BBC”和“FBI”两个字母块。当个体需要在随机摆放的众多字母中正确识别这6个字母位置时, 性能组件会先检测所有字母的位置布局, 然后识别原有存储在长时记忆中“BBC”与“FBI”这两个字母块所在正确位置后将其调取到短时记忆临时存储, 最后将短时记忆中临时存储的两个字母块进行调取以排除多余字母后, 正确选择这6个字母的位置。

图1 MAPP流程图
虽然, 组块理论提出了完整的对块信息的提取和编码系统, 但它依旧存在三点缺陷。(1)没有对短时记忆和工作记忆进行区分。从记忆功能的角度来看, 短时记忆以存储功能为主, 信息编码功能发生在工作记忆中。而组块理论虽然是基于短时记忆所提出, 但其性能组件中的短时记忆编码子系统的操作过程更接近工作记忆的运作机制。因此, 该理论模型更应该视为一种初级工作记忆的组块运行机制。(2) Chase和Simon (1973)认为创建一个新的块需要8s, 而将新的块添加到已有数据块中需要2s, 创建新块的时间较长, 速度较慢, 这就无法解释专家对大量信息的快速存储以及即时回忆的情况。(3)无法解释在工作记忆容量较小的情况下, 专家可以使用复杂的新信息完成任务的现象(Gobet & Simon, 1998)。因此, 在Simon的基础上, Gobet提出了模板理论。
4.2 模板理论(Template theory)
Gobet基于由短时记忆组成的CHREST (Chunk Hierarchy and Retrieval Structures)计算模型, 提出模板理论。CHREST模型包括3个按照先后顺序排列的子系统, 以对围棋布局的加工为例, 首先, 个体通过视觉感知系统, 输入棋子布局信息; 其后, 输入的信息将被保存在类似视觉短时记忆存储的中间设备中; 最后, 短时记忆中经常被接触到的棋子信息将会进一步被重新编码形成块被存储在长时记忆中, 这些块被用作固定模板并在后期需要时被调取进入短时记忆备用(Bennett et al., 2020)。相比MAPP模型, 模板理论增加了两种新机制: (1)新的平行节点。原有节点用以编码感觉信息, 新增节点则编码动作信息, 两种节点在一定程度上可以彼此连接形成新的结构; (2)检索结构。用以自动获取被快速编码的块(retrieval structure), 经常接触的块会发展为带有插槽的模板(templates), 新信息可以自动添加到模板上, 插槽的作用则在于判别和测试新信息是否适合原有模板, 提高了组块效率的同时也丰富已有模板(Gobet et al., 2001) (详见图2)。例如, 个体首先被要求识记2 0 1 8这4个数字块, 视觉信息先将4个数字块临时保存在短时记忆中, 后被重新编码为“2018年”一个字符块被存储于长时记忆中。在此之后, 如果要求个体再次记忆8 3 1这3个数字块时, 个体会将这4个数字块作为新增节点与原有的“2018年”字符块形成新的连接后再次被编码为“2018年8月31日”一个更大的字符块。该字符块可以被不断复述成为长时记忆中的模板, 在后期需要回忆2 0 1 8 8 3 1这7个数字块时可以被整体调取。
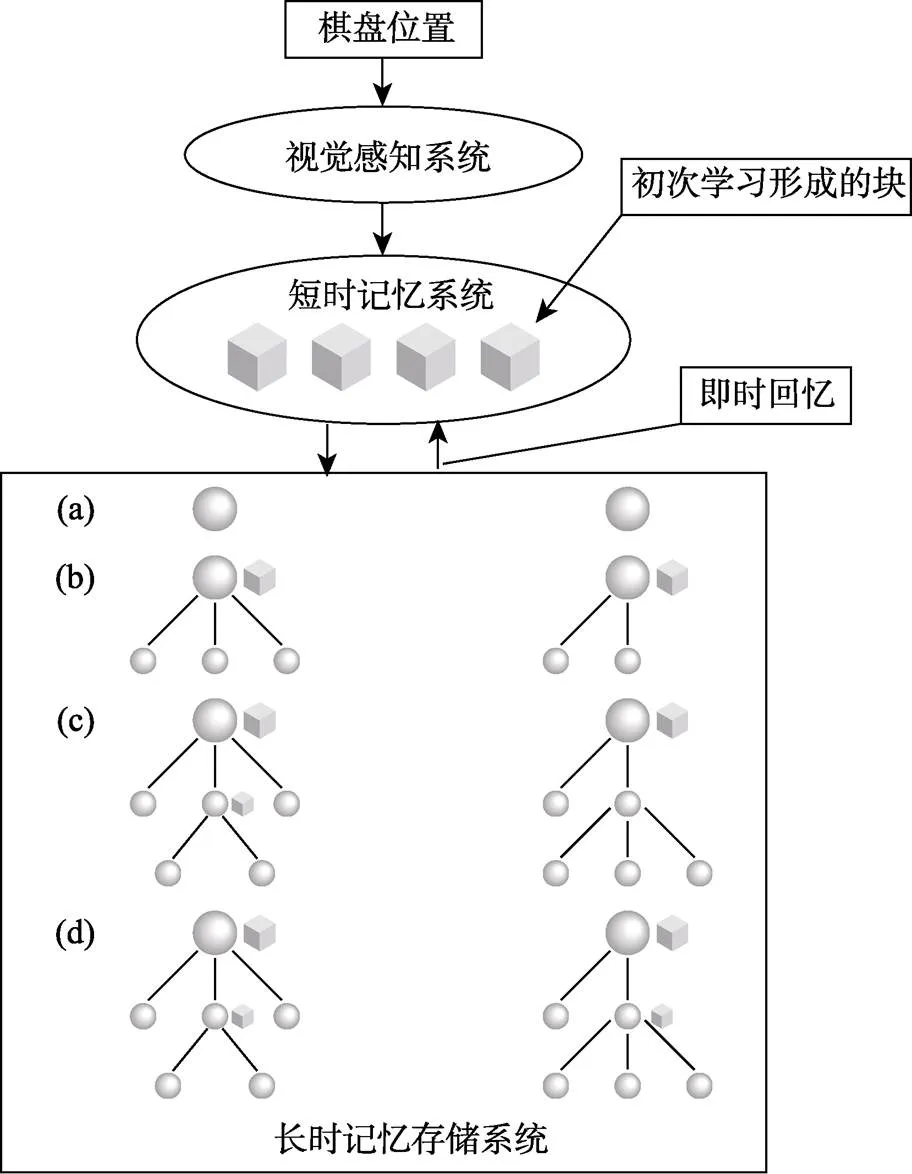
图2 CHREST流程图。长时记忆存储系统中: (a)表示两个模板最初的节点, 左侧节点代表感觉信息, 右侧节点代表行为信息; (b)菱形表示插槽, 用来测试新信息, 测试通过的新信息将会创建新的节点和连接; (c)随着信息的增长, 两个模板都在不断增加分支; (d)两个模板中的节点可以通过相似性相互连接。
资料来源: 部分引自Gobet(2005).
模板理论所提出的插槽结构, 解释了个体在短时间内对大量复杂信息快速组块和即时回忆的现象, 同时其运行过程与工作记忆对信息的加工过程类似。因此, 研究者认为模板理论比组块理论更加全面描述了工作记忆的组块机制, 但该模型存在以下两个缺点: (1)依旧没有将工作记忆作为一个独立的组块加工系统; (2)缺乏一个注意系统。由于个体注意资源的限制, 不能平行处理多个块信息, 工作记忆中的信息与长时记忆中插槽的连接也需要注意的参与(Guida et al., 2012)。直至Cowan的“工作记忆的嵌入式过程模型”被提出, 工作记忆才被当作相对独立的组块加工系统。
4.3 工作记忆的嵌入式过程模型(Embedded- processes model of working memory)
Cowan (1998)将长时记忆、工作记忆融为一体, 认为工作记忆不再是一个独立的记忆系统, 而是由容量有限的焦点、注意系统以及长时记忆中被临时激活的区域组成。其运作过程为: 信息首先激活短暂的感觉记忆, 之后感觉记忆进一步激活长时记忆中的焦点(Cowan, 2019), 焦点受到所处的不同环境与个体的注意力范围大小所控制(Cowan, 2016), 众多感官功能尤其是语义功能都能激活焦点。此后, 个体可以对焦点包含的信息进行自动访问, 不在焦点中但与焦点紧密相连的其它信息通过扩大注意力范围也可以被间接访问(Cowan et al., 2018)。注意力范围具有灵活性, 个体可以对其进行调整以适应不同任务需要(Cowan et al., 2020)。这其中, 注意力范围最多可以同时容纳4个简单块, 当遇到较为复杂的块时, 添加相关信息可以协助处理该复杂块(Verhaeghen et al., 2004)。虽然长时记忆中焦点的激活量没有限制, 但只有被注意到的焦点才能被轻松激活(Cowan et al., 2021)。被激活的焦点会与新的信息重新编码整合形成超级块作为长时记忆的一部分被保留下来, 整个过程既提高了组块效率也增加了对块的记忆容量(Cowan, 2010)。
该模型系统阐述了工作记忆的组块加工机制, 并将其体现在对长时记忆中注意焦点的整合和提取中。Hitch等人(2019)虽然没有反对工作记忆是长时记忆的一部分这一观点, 但却认为不能否定工作记忆独有作用, 应该区别工作记忆与长时记忆两个系统同时又关注二者之间的联系。有研究发现, 新信息在没有形成焦点的情况下, 依旧可以被个体进行组块后提取, 由此说明新信息并没有被存储在长时记忆中, 而嵌入式过程模型无法解释该信息所能存储的位置, 说明确实存在一个临时的与长时记忆分离的存储系统(Baddeley et al., 2019)。与此同时, Norris (2017)认为长时记忆不能代替工作记忆的重要证据来自于对工作记忆严重受损患者, 实验发现, 患者能够回忆出已经习得且较为熟练的单词, 但对新学习的单词的回忆却较为困难。证明长时记忆和工作记忆是两个相互独立的系统, 因此, 应该重视工作记忆自身功能的观点。
以上三种模型都认可长时记忆对组块的影响, 但模板理论所包含的插槽使其比组块理论模型能更多、更快地加工信息碎片, 嵌入式模型的注意焦点则限制了复述对块的数量的作用。因此, 接下来将对三种理论下所提出的不同块容量进行讨论。
4.4 块的容量
导致工作记忆中块容量暂无统一标准的关键原因是能否在块容量的计算过程中使用策略。组块理论和模板理论并没有反对在组块过程中使用策略。组块理论认为学习者通过不断的使用复述策略将信息构造成多种类型的块, 成为一个庞大的数据库存储在长时记忆中(Gobet & Simon, 1998)。专家至少在长时记忆中存储了大约50000个数据块, 一旦进行学习和回忆, 数据块会被快速访问, 并通过短时记忆(包含工作记忆)将新信息和原有块信息整合成更大块信息(Chase & Simon, 1973)。因此, 虽然同样受短时记忆容量限制, 但专家所拥有的块容量远大于新手(Pluss et al., 2019)。针对短时记忆(包含工作记忆)容量大小的问题, Chase和Simon (1973)认为, 被试在初次回忆时会保存较大且粗糙的块, 第二阶段会根据信息之间的联系, 重建块的构造, 因此, 在实验中, 棋手能够回忆大约7个块。同样, 模板理论中模板的形成也是由于个体对信息的复述策略导致, 经验越丰富的个体所形成的模板越稳定, 新信息越能快速与模板中的插槽相结合并重新编码形成更大的块。虽然模板理论认为短时记忆(包含工作记忆)中的模板容量大约为3个块左右(Smith et al., 2021), 但同时也提出, 快速编码只有在填充插槽的过程中才会发生, 否则其信息编码速度和块数量与组块理论并无区别(Gobet & Clarkson, 2004)。与上述观点相反, 另有研究者认为在计算工作记忆块容量的时候不应该使用策略。
Cowan (2021)认为, 受注意资源的限制, 长时记忆焦点中的块容量不能多于4个。例如, 数字12345678可以快速重新编码为12, 34, 56, 78四个大块。Miller所使用的测量方法, 在短时记忆容量达到上限时, 可以通过复述策略将没有客观联系的信息整合成块, 没有真正体现纯粹的工作记忆块数量, 导致越是富有经验的个体的工作记忆容量越大, 违背了固定容量限制的前提(Cowan, 2020), 因此, Miller对短时记忆(包含工作记忆)块容量的计算并不被认可 (Bhandari & Badre, 2018)。Mathy和Feldman (2012)也提出, 7个块的容量是复述策略下的复合容量, 而4个块是经过压缩, 未使用任何助记形式的真实的记忆容量。因此, 需要在实验中排除策略对块形成的影响, 从而正确识别工作记忆的容量上限, 以获取纯粹的块数量(Bayliss et al., 2003)。由此, Cowan提出4种能准确测量工作记忆块容量上限的方法: (1)当个体在记忆过程中, 将块拆分成单个事物进行记忆时, 证明已经达到记忆容量限制。(2)采取其它方法阻止对块的重新编码。(3)在组块过程中因为容量的限制导致效率降低时, 证明已经达到容量最高限制。(4)若工作记忆对信息的存储和加工效率下降, 则表明达到容量上限(Cowan, 2016)。
计算工作记忆的容量上限成为组块研究中不可回避的话题, 同时也有研究者提出过载的块容量会降低信息加工的灵活性以及精确度, 导致个体无法同时兼顾多个重要任务(Perfors, 2012)。因此, 如何在工作记忆中保存合理的块数量的问题也需要后期的研究给予关注。
5 展望
5.1 长时记忆与组块机制的关系
现有对组块机制研究的争议主要是长时记忆与组块机制的关系, 研究者对此提出以下两点展望: (1)不能忽略长时记忆对工作记忆中组块机制的作用。首先, Mille只将块作为简单的含有信息的模块, 仅简单地描述了块在短时记忆中的编码、存储和提取过程, 并没有明确提出有关组块机制的理论, 且没有提及长时记忆在短时记忆(包含工作记忆)组块过程中起到的作用。但Chase和Simon (1973)在基于Miller的组块研究所提出的组块理论中, 指出长时记忆可以为短时记忆(包含工作记忆)中信息的组块提供所需要的组块模式信息, 长时记忆为工作记忆提供过去经验从而协助组块机制的运行。其次, 有研究者认为块的形成是过去经验和当前信息连接的结果, 块更可能被存储于长时记忆中, 工作记忆是组块机制运行的场所(Gobet et al., 2001)。因此长时记忆不能被排除在工作记忆组块运行机制之外。(2)需要继续探讨长时记忆对工作记忆中的块编码和存储过程中所产生的影响程度。首先, Baddeley等人(2019)认为, 长时记忆只为工作记忆组块过程提供过去经验知识, 至于块的编码和存储仅发生在工作记忆中。情境缓冲器作为中央执行系统和长时记忆之间的接口, 是信息进行组块和存储的位置所在, 其运行过程并不受注意资源的影响而单纯受情景缓冲器容量的影响。根据fMRI的测试, 工作记忆所包含的语音环路、中央执行系统、视觉空间模板三个子系统拥有独立的脑区, 工作记忆中块的编码过程可以在这三个系统中运行而不受长时记忆的影响(Hitch et al., 2019)。同样, 有研究者也认为视觉和听觉信息会在工作记忆中构建和整合, 长时记忆仅在块构建的后期发挥提供经验知识的作用(Darolia & Varshney, 2016)。但Cowan (2019)则认为, 长时记忆参与工作记忆中组块的编码过程, 在此过程中提供着重要的注意力资源以协助块的整合。并且块在构造完成后会被存储于长时记忆中, 只有块被需要时才会被激活后临时存储于工作记忆以供使用。同时, Ericsson和Kintsch (1995)等人所提出的长时工作记忆概念也认同块的编码与存储发生在长时记忆中。专家比新手熟练的原因主要在于长时记忆中存储着众多成熟块, 新信息在长时记忆中与已有块编码整合后形成更大的块, 专家更能够熟练地利用外部线索将块提取到工作记忆中备用以应对当前任务。另有研究者通过实证研究表明, 工作记忆中的信息被激活的同时, 长时记忆中与其相关联的信息也同时被激活, 个体对信息的编码离不开长时记忆的帮助(刘兆敏, 郭春彦, 2013)
5.3 完善不同年龄阶段组块特征
现有对不同年龄阶段个体的组块研究主要集中在婴幼儿时期和成人时期, 未来研究应该对个体一生各个年龄阶段的组块发展趋势和特征进行研究。可从以下两个方面进行深入探讨: (1)块的层级转换是否发生在几个固定的年龄区间中?随着年龄的增长, 生理和环境因素对块的层级转换影响的比重是否存在动态变化?(2)对童年期、青少年期和老年期的块特征研究还较为缺乏。有少数研究发现, 通过让老年人学习不同蔬菜所包含的化学物质概念, 并且通过概念分类任务对老年人的学习成果进行测试。结果发现, 老年人虽然工作记忆有所衰退, 但相对于成人, 老年人运用了更多的过去经验将新的知识进行概念整合, 从而创造了更大的工作记忆存储空间来弥补自身工作记忆衰退带来的影响(Soederberg et al., 2011)。但该研究并未明确老年人运用过去经验进行组块与成年人之间存在何种差异。因此, 对不同年龄阶段个体的块特征的研究需要从块的编码、存储和提取过程入手, 以揭示组块的年龄特点。
5.2 “复述策略”与“少即是多”原则对块容量的影响
针对个体工作记忆中块容量是否存在确定数值区间的问题暂无一致的结论, 未来研究可以从以下两个方面进行思考: (1)复述策略是否是造成工作记忆中块容量区间大幅度变化的关键原因?虽然Cowan (2019)自始至终对此持肯定态度, 但Berry等(2018)的研究却表明, 在抑制和不抑制复述策略的前提下, 缓慢或快速呈现列表中需要记住的项目, 被试核心记忆容量都为3到4个块, 这与Cowan观察到的数量大致相似。研究者认为, 工作记忆中存在固定数量的块, 复述策略可能只会对组块过程造成影响, 从而导致整体的块连接形式处在动态变化中, 使记忆更具有灵活性以应对不同情境下对特定信息的需要, 并不会对工作记忆的块容量产生影响。Unsworth和Engle (2007)提出, 工作记忆包含着初级记忆系统(Primary Memory)和次级记忆系统(Secondary Memory)。其中, 初级记忆系统在注意力的维护下长期存储着4个块, 而次级记忆系统可以从长时记忆中调取初级记忆系统所需要的额外信息, 从而达到更新块的目的。已有研究表明, 在体育运动过程中, 专家的成绩之所以高于新手的原因在于, 相比新手在运动中只运用了程序性记忆, 专家更多地使用了陈述性记忆, 可以有意识地运用策略不断变换工作记忆中块之间的连接方式, 从而更能灵活应对不同的比赛形式(Christensen et al., 2019)。因此, 复述策略可能是引起块之间连接形式的关键因素, 对块容量可能并不产生影响。
(2)不能把尽可能扩展工作记忆的块容量作为提高工作记忆运行效率的根本目标, 今后的研究不仅要探讨工作记忆中块的容量范围, 也应该探讨一个能最大限度发挥组块功能的容量范围, 以保证人们认知活动质量的最大化。尽管提高工作记忆容量可以促进和提高个体对问题解决(张帆等, 2018)、阅读(倪锦诚, 2017)等高级认知活动的效率和质量。但有学者提出, 儿童比成年人能成为更好的第二语言学习者的一种假设是: 虽然儿童的组块数量远低于成年人, 但儿童却能更好的将注意资源集中在每个块所包含的语言信息碎片中, 而成年人的工作记忆中含有大量块, 在语言学习中会更注重整体而忽视较为细节的部分, 从而导致语言学习效率以及准确度不及儿童(Gordon et al., 2020)。Newport (1990)提出“少即是多”假设, 认为机体不成熟的年幼语言学习者, 更容易在每次学习中抓住少部分语言信息, 这有助于在复杂的语言学习环境中, 将语言信息分解成很多细小的结构, 学习过程会更加精确。因此, 研究者认为, 现今学术界大多只关注工作记忆中块数量的上下限问题, 忽略了每个块都是由多个信息碎片组成这一特点。对块的存储和提取以及对信息碎片的分析都需要运用意识资源, 过多的块会占用意识资源, 从而使人们忽略单个块中部分信息细节, 即使提取了大量块, 也会降低块的使用质量。
黄福荣, 和美, 罗劲. (2017). 组块破解形态顿悟的脑认知机理.,(31), 11.
刘兆敏, 郭春彦. (2013). 工作记忆和长时记忆共享信息表征的ERP证据.,(3), 276–284.
倪锦诚. (2017). 交互记忆阅读策略对二语工作记忆容量的影响.,(5), 49–53.
彭聃龄. (2019).(第5版). 北京师范大学出版社.
张帆, 杨超群, 夏云曼, 桑娜, 王小刚, 毕泰勇, 邱江. (2018). 视觉工作记忆内容维持的大脑神经机制.,(27), 2883-2895.
Alluhaybi, I., & Witzel, J. (2020). Letter connectedness and Arabic visual word recognition.,(10), 1660–1674.
Applin, J. B., & Kibbe, M. M. (2021). Young children monitor the fidelity of visual working memory.,(5), 808–819.
Atkinson, R. C., & Shiffrin, R. M. (1968). Human memory: A proposed system and its control processes1.,, 89–195.
Baddeley, A. (2003). Working memory: Looking back and looking forward.,(10), 829–839.
Baddeley, A. D., Hitch, G. J., & Allen, R. J. (2019). From short-term store to multicomponent working memory: The role of the modal model.,(4), 575–588.
Bayliss, D. M., Jarrold, C., Gunn, D. M., & Baddeley, A. D. (2003). The complexities of complex span: Explaining individual differences in working memory in children and adults.,(1), 71–92.
Bennett, D., Gobet, F., & Lane, P. (2020, August).. Paper presented at the Proceedings of the 42nd Annual Meeting of the Cognitive Science Society, Virtual.
Berry, E. D. J., Waterman, A. H., Baddeley, A. D., Hitch, G. J., & Allen, R. J. (2018). The limits of visual working memory in children: Exploring prioritization and recency effects with sequential presentation.,(2), 240–253.
Bhandari, A., & Badre, D. (2018). Learning and transfer of working memory gating policies.,, 89–100.
Chase, W. G., & Simon, H. A. (1973). Perceptions in chess.,(1), 55–81.
Chekaf, M., Cowan, N., & Mathy, F. (2016). Chunk formationin immediate memory and how it relates to data compression.,, 96–107.
Christensen, W., Sutton, J., & Bicknell, K. (2019). Memory systems and the control of skilled action.,(5), 692–718.
Cowan, N. (1998). Attention and memory: An integrated framework. In Cary (Series Ed.).s (No. 26). New York: Oxford University Press.
Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity.,(1), 87–114.
Cowan, N. (2010). The magical mystery four: How is working memory capacity limited, and why?,(1), 51–57.
Cowan, N. (2016). The many faces of working memory and short-term storage.,(4), 1158–1170.
Cowan, N. (2019). Short-term memory based on activated long-term memory: A review in response to norris (2017).,(8), 822–847.
Cowan, N. (2020). Why and how to study working memory development.,(2), 135–156.
Cowan, N., AuBuchon, A. M., Gilchrist, A. L., Blume, C. L., Boone, A. P., & Saults, J. S. (2021). Developmental change in the nature of attention allocation in a dual task.,(1), 33–46.
Cowan, N., Belletier, C., Doherty, J. M., Jaroslawska, A. J., Rhodes, S., Forsberg, A., … Logie, R. H. (2020). How do scientific views change? Notes from an extended adversarial collaboration.,(4), 1011–1025.
Cowan, N., Li, Y., Glass, B. A., & Scott Saults, J. (2018). Development of the ability to combine visual and acoustic information in working memory.,(5), e12635. http://doi.org/10.1111/desc.12635
Darolia, C. R., & Varshney, N. (2016). Role of long-term memory activation in working memory.,(1), 153.
Ding, X., Gao, Z., & Shen, M. (2017). Two equals one: Two human actions during social interaction are grouped as one unit in working memory.,(9), 1311–1320.
Ericsson, K. A., & Kintsch, W. (1995). Long-term working memory.,(2), 211–245.
Feigenson, L., Libertus, M. E., & Halberda, J. (2013). Links between the intuitive sense of number and formal mathematics ability.,(2), 74–79.
Forsberg, A., Guitard, D., & Cowan, N. (2021). Working memory limits severely constrain long-term retention.,(2), 537–547.
Gobet, F. (2005). Chunking models of expertise: Implications for education.,(2), 183–204.
Gobet, F., & Clarkson, G. (2004). Chunks in expert memory: Evidence for the magical number four ... or is it two?,(6), 732–747.
Gobet, F., Lane, P. C. R., Croker, S., Cheng, P. C., Jones, G., Oliver, I., & Pine, J. M. (2001). Chunking mechanisms in human learning.,(6), 236– 243.
Gobet, F., & Simon, H. A. (1998). Expert chess memory: Revisiting the chunking hypothesis.,(3), 225– 255.
Gordon, R., Smith-Spark, J. H., Newton, E. J., & Henry, L. A. (2020). Working memory and high-level cognition in children: An analysis of timing and accuracy in complex span tasks.,, 104736.
Guida, A., Fartoukh, M., & Mathy, F. (2020). The development of working memory spatialization revealed by using the cave paradigm in a two-alternative spatial choice.,(1), 54–70.
Guida, A., Gobet, F., Tardieu, H., & Nicolas, S. (2012). How chunks, long-term working memory and templates offer a cognitive explanation for neuroimaging data on expertise acquisition: A two-stage framework.,(3), 221–244.
Hitch, G. J., Allen, R. J., & Baddeley, A. D. (2019). Attention and binding in visual working memory: Two forms of attention and two kinds of buffer storage.,(1), 280–293.
James, W. (1891). The moral philosopher and the moral life.,(3), 330–354.
Kibbe, M. M., & Feigenson, L. (2014). Developmental origins of recoding and decoding in memory.,, 55–79.
Kibbe, M. M., & Leslie, A. M. (2019). Conceptually rich, perceptually sparse: Object representations in 6-month-old infants' working memory.,(3), 362–375.
Kingo, O. S., & Krøjgaard, P. (2012). Object function facilitates infants' object individuation in a manual search task.,(2), 152– 173.
Malmberg, K. J., Raaijmakers, J. G. W., & Shiffrin, R. M. (2019). 50 years of research sparked by Atkinson and Shiffrin (1968).,(4), 561–574.
Mathy, F., & Feldman, J. (2012). What’s magic about magic numbers? Chunking and data compression in short-term memory.,(3), 346–362.
Mclean, R. S., & Gregg, L. W. (1967). Effects of induced chunking on temporal aspects of serial recitation.,(4,Pt.1), 455–459.
Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information.,(2), 81–97.
Newport, K. T. (1990, June).. Paper presented at the Infocom 90, Ninth Joint Conference of the IEEE Computer & Communication Societies the Multiple Facets of Integration, San Francisco, CA, USA: IEEE.
Norris, D. (2017). Short-term memory and long-term memory are still different.,(9), 992–1009.
Peng, P., Barnes, M., Wang, C., Wang, W., Li, S., Swanson, H. L., … Tao, S. (2018). A meta-analysis on the relation between reading and working memory.,(1), 48–76.
Perfors, A. (2012). When do memory limitations lead to regularization? An experimental and computational investigation.,(4), 486–506.
Pförtner, P., & Hristova, P. (2021). Thematic bootstrapping: Performance differences between expert chess players and novices.,(1), 55–68.
Pluss, M. A., Bennett, K. J. M., Novak, A. R., Panchuk, D., Coutts, A. J., & Fransen, J. (2019). Esports: The chess of the 21st century.,, 156.
Rosenberg, R. D., & Feigenson, L. (2013). Infants hierarchically organize memory representations.,(4), 610–621.
Sala, G., Burgoyne, A. P., Macnamara, B. N., Hambrick, D. Z., Campitelli, G., & Gobet, F. (2017). Checking the “Academic Selection” argument. Chess players outperform non-chess players in cognitive skills related to intelligence: A meta-analysis.,, 130–139.
Sala, G., & Gobet, F. (2017). Does far transfer exist? Negative evidence from chess, music, and working memory training.,(6), 515– 520.
Simon, H. A., & Barenfeld, M. (1969). Information- processing analysis of perceptual processes in problem solving.,(5), 473–483.
Smalle, E. H. M., Bogaerts, L., Simonis, M., Duyck, W., Page, M. P. A., Edwards, M. G., & Szmalec, A. (2015). Can chunk size differences explain developmental changes in lexical learning?,, 1925.
Smith, E. T., Bartlett, J. C., Krawczyk, D. C., & Basak, C. (2021). Are the advantages of chess expertise on visuo- spatial working-memory capacity domain specific or domain general?,(8), 1600–1616.
Soederberg Miller, L. M., Gibson, T. N., Applegate, E. A., & de Dios, J. (2011). Mechanisms underlying comprehension of health information in adulthood: The roles of prior knowledge and working memory capacity.,(5), 794–806.
Stahl, A. E., & Feigenson, L. (2014). Social knowledge facilitates chunking in infancy.,(4), 1477–1490.
Stahl, A. E., & Feigenson, L. (2018). Infants use linguistic group distinctions to chunk items in memory.,, 149–167.
Unsworth, N., & Engle, R. W. (2007). The nature of individual differences in working memory capacity: Active maintenance in primary memory and controlled search from secondary memory.,(1), 104–132.
Verhaeghen, P., Cerella, J., & Basak, C. (2004). A working memory workout: How to expand the focus of serial attention from one to four items in 10 hours or less.,(6), 1322–1337.
Wang, J. J., & Feigenson, L. (2019). Infants recognize counting as numerically relevant.,(6), e12805.http://doi.org/10.1111/desc.12805
The development of concept and theoretical models of “chunking” in working memory
CHEN Yutian, CHEN Rui, LI Peng
(Faculty of Education, Yunnan Normal University, Kunming 650500, China)
After a miracle principle of '7±2 chunks' which was proposed by Miller, chunking was considered as one of the most effective memory strategies, and it is a matter of great concern about working memory. Although previous researches have confirmed that chunking can increase the capacity of working memory, there are debates on the concept of chunking, the relationship between the structures of chunking and development of age, chunking capacity, and its works mechanism. Therefore, this paper aimed to discuss on all above issues. In the future, it is worth to focus on the role of long-term memory during chunking in working memory, the features of chunks at the stages of ages, and develop the advantage of the principle of “less is more”.
chunking, working memory, structure, capacity
2022-01-13
陈玉田和陈睿共同第一作者
李鹏, E-mail: Lee@ynnu.edu.cn
B842

