与三个数论函数有关的一个方程的整数解

姜莲霞,张四保,傅 湧

(1.喀什大学 数学与统计学院,新疆 喀什 844008;2.宜春学院 数学与计算机科学学院,江西 宜春 336000)

φ2(φ4(m))=2ω(m)

(1)

的整数解问题,利用广义Euler函数φ2(m)与广义Euler函数φ4(m)的性质,得到这一方程的一切整数解。

1 几个基本引理

引理1[13]当m≥3时,有φ(m)为偶数。

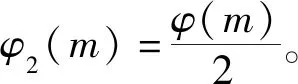
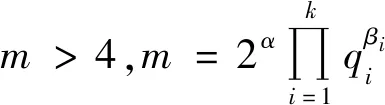
2 定理及其证明

定理1 方程(1)的一切正整数解为m=41,43,64,77,85,93,119,123,136,141,147,153,158,164,194,255,340,374,402,408,410,442,476,492,498,520,574,582,610,612,650,738,1 020,1 122,1 230,1 326,1 428,1 560,1 530,1 722,1 830,1 950。

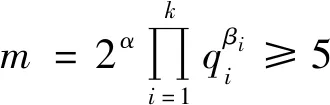
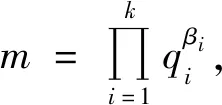
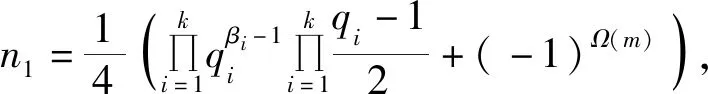
(2)

当πO时,式(2)有解k=1、β1=1、q1=11,此时m=11。经验证m=11不是方程(1)的整数解。当πE时,式(2)有解k=1、β1=2、q1=3与k=2、β1=β2=1、q1=3、q2=7,此时m=32=9,m=3×7=21。经验证m=9与m=21不是方程(1)的整数解。因而n1≥2,则2ω(m)n1≥4,结合引理2,由方程(1)得φ(2ω(m)n1)=2ω(m)+1,因而有

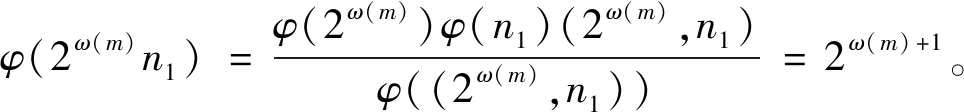
(3)

当(2ω(m),n1)=1时,由式(3)得φ(n1)=22,则n1=5,则有

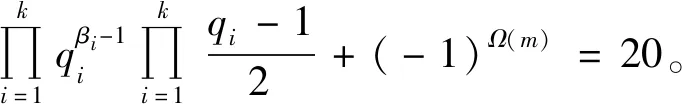
(4)

当πO时,式(4)有解k=1、β1=1、q1=43与k=2、q1=3、q2=7、β1=1、β2=2,此时m=43,m=3×72=147。经验证m=43与m=147都是方程(1)的整数解。当πE时,式(4)无奇素数解。

当(2ω(m),n1)=2ε1时,令n1=2ε1η1,其中(2,η1)=1,则由式(3)得φ(η1)=22-ε1,因而ε1=1,2。

当ε1=1时,有φ(η1)=2,则η1=3,因而n1=2×3=6,从而有

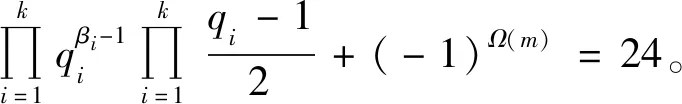
(5)

当πO时,式(5)无奇素数解。对于式(5),当πE时,式(5)有解k=2、β1=β2=1、q1=3、q1=47,此时m=3×47=141。经验证m=141是方程(1)的整数解。

当ε1=2时,有φ(η1)=1,则η1=1,因而n1=22=4,从而有

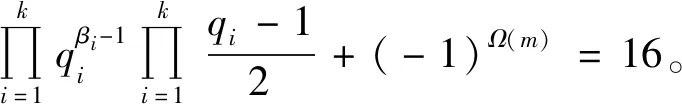
(6)

当πO时,式(6)无奇素数解。当πE时,式(6)有解k=2、β1=β2=1、q1=3、q2=31与k=2,β1=β2=1、q1=7、q2=11,此时m=3×31=93,m=7×11=77。经验证m=93,m=77是方程(1)的整数解。

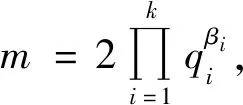
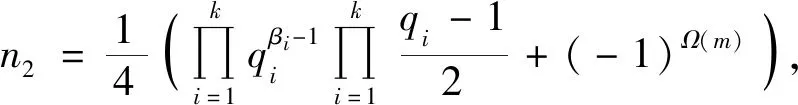
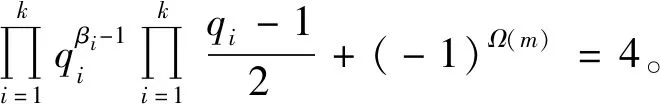
(7)

当πO时,式(7)有解k=2、β1=β2=1、q1=3、q2=11,此时m=2×3×11=66。经验证m=66不是方程(1)的整数解。当πE时,式(7)有解k=1、β1=1、q1=7,此时m=2×7=14。经验证m=14不是方程(1)的整数解。因而n2≥2,则2kn2≥4,结合引理2,由方程(1)得φ(2kn2)=2k+2,因而有

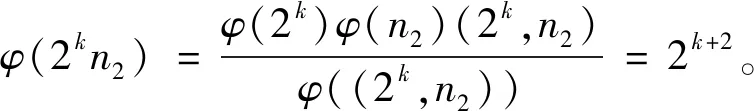
(8)

当(2k,n2)=1时,由式(8)有φ(2k)φ(n2)=2k+2,则φ(n2)=23,因而n2=15,从而

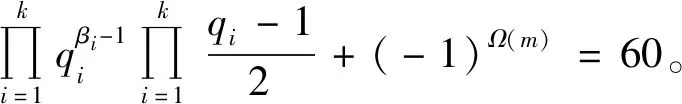
(9)

当πO与πE时,式(9)无奇素数解。

当(2ω(m),n2)=2ε2时,令n2=2ε2η2,其中(2,η2)=1,则由式(8)得φ(η2)=23-ε2,因而ε2=1,2,3。

当ε2=1时,有φ(η2)=22,则η2=5,因而n2=2×5=10,从而有

(10)

当πO时,式(10)有解k=2、β1=β2=1、q1=3、q2=83,此时m=2×3×83=498。经验证m=498是方程(1)的整数解。当πE时,式(10)有解k=1、β1=1、q1=79,此时m=2×79=158。经验证m=158是方程(1)的整数解。

当ε2=2时,有φ(η2)=2,则η2=3,因而n2=22×3=12,从而有

(11)

当πO与πE时,式(11)均无奇素数解。

当ε2=3时,有φ(η2)=1,则η2=1,因而n2=23=8,从而有

(12)

当πO时,式(12)有解k=2、β1=β2=1、q1=3、q2=67,此时m=2×3×67=402。经验证m=402是方程(1)的整数解。对于式(12),当πE时,式(12)无奇素数解。

情况3 当m为其他情况,此时m或为奇数或为偶数。

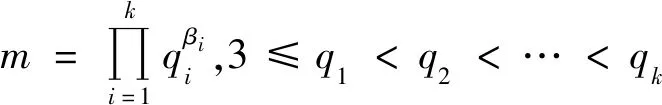
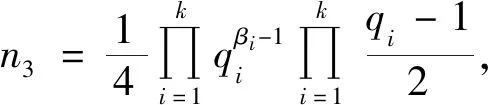
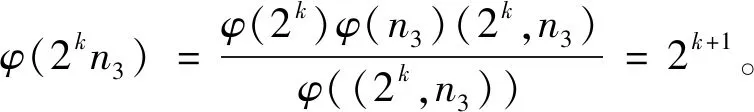
(13)

当(2k,n3)=1,由式(13)有φ(2kn3)=φ(2k)φ(n3)=2k+1,从而φ(n3)=22,则n3=5,因而有

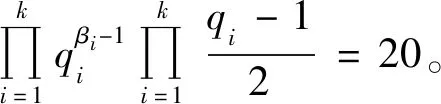
(14)

此时式(14)有解k=1、β1=1、q1=41与k=2、β1=β2=1、q1=3、q2=41,此时m=41,m=3×41=123。经验证m=41与m=123都是方程(1)的整数解。

当(2k,n3)=2ε3时,令n3=2ε3η3,其中(2,η3)=1,则由式(13)有φ(η3)=22-ε3,因而ε3=1,2。

当ε3=1时,有φ(η3)=2,则有η3=3,因而n3=2×3=6,从而有

(15)

此时式(15)有解k=2、β1=β2=1、q1=7、q2=17与k=2、β1=2、β2=1、q1=3、q2=17,此时m=7×17=119,m=32×17=153。经验证m=119,m=153是方程(1)的整数解。

当ε3=2时,有φ(η3)=1,则有η3=1,因而n2=22=4,从而有

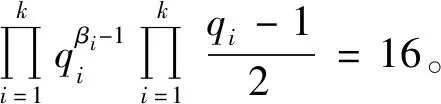
(16)

此时式(16)有解k=2、β1=β2=1、q1=5、q2=17与k=3、β1=β2=β3=1、q1=3、q2=5、q3=17,此时m=5×17=85,m=3×5×17=255。经验证m=85,m=255是方程(1)的整数解。

情况3.2m为偶数。

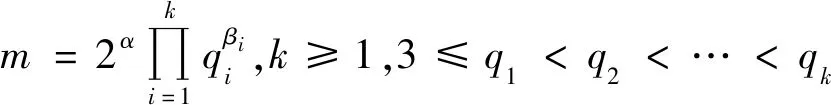
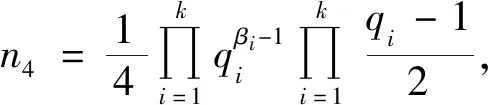
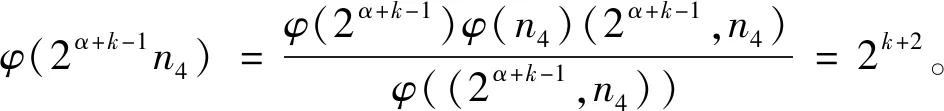
(17)

当(2α+k-1,n4)=1,由式(17)得φ(2α+k-1)φ(n4)=2k+2,从而φ(n4)=24-α,得α=1,2,3,4。

当α=1时,有φ(n4)=23,则n4=15,因而有

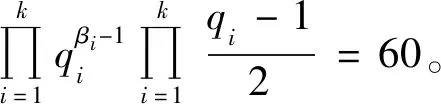
(18)

此时式(18)有解k=2、β1=β2=1、q1=5、q2=61与k=2、β1=β2=1、q1=7、q2=41与k=2、β1=2、β2=1、q1=3、q2=41与k=2、β1=2、β2=1、q1=5、q2=13与k=3、β1=β2=β3=1、q1=3、q2=5、q3=61与k=3、β1=β2=β3=1、q1=3、q2=7、q3=41与k=3、β1=1、β2=2、β3=1、q1=3、q2=5、q3=13,此时m=2×5×61=610,m=2×7×41=574,m=2×32×41=738,m=2×52×13=650,m=2×3×5×61=1 830,m=2×3×7×41=1 722,m=2×3×52×13=1 950。经验证m=610,m=574,m=738,m=650,m=1 830,m=1 722,m=1 950是方程(1)的整数解。

当α=2时,有φ(n4)=22,则n4=5,因而有

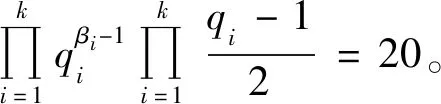
(19)

此时式(19)有解k=1、β1=1、q1=41与k=2、β1=β2=1、q1=3、q2=41,此时m=22×41=164,m=22×3×41=492。经验证m=164,m=492是方程(1)的整数解。

当α=3时,有φ(n4)=2,则n4=3,因而有

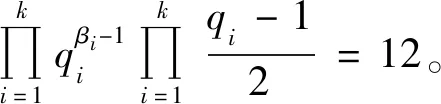
(20)

此时式(20)有解k=2、β1=β2=1、q1=5、q2=13与k=3、β1=β2=β3=1、q1=3、q2=5、q3=13,此时m=23×5×13=520,m=23×3×5×13=1 560。经验证m=520,m=1 560是方程(1)的整数解。

当α=4时,有φ(n4)=1,则n4=1,因而有

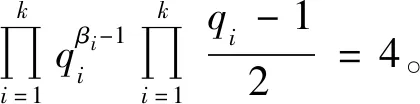
(21)

此时式(21)无奇素数解。

当(2α+k-1,n4)=2ε4时,令n4=2ε4η4,其中(2,η4)=1,则由式(17)得φ(η4)=24-α-ε4,因而α+ε4=2,3,4。

当α+ε4=2时,有α=ε4=1,此时φ(η4)=22,则η4=5,有n4=10,因而有

(22)

此时式(22)有解k=2、β1=β2=1、q1=5、q2=41与k=3、β1=β2=β3=1、q1=3、q2=5、q3=41与k=2、β1=β2=1、q1=11、q2=17与k=3、β1=β2=β3=1、q1=3、q2=11、q3=17,此时m=2×5×41=410,m=2×3×5×41=1 230,m=2×11×17=374,m=2×3×11×17=1 122。经验证m=410,m=1 230,m=374,m=1 122是方程(1)的整数解。

当α+ε4=3时,有α=1,ε4=2或者α=2,ε4=1,此时φ(η4)=2,有η4=3。

当α=1,ε4=2时,有n4=12,因而有

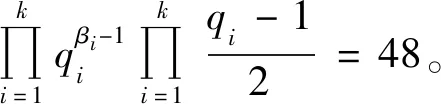
(23)

此时式(23)有解k=1、β1=1、q1=97与k=2、β1=β2=1、q1=3、q2=97与k=3、β1=2、β2=β3=1、q1=3、q2=5、q3=17与k=2、β1=β2=1、q1=13、q2=17与k=3、β1=β2=β3=1、q1=3、q2=13、q3=17,此时m=2×97=194,m=2×3×97=582,m=2×32×5×17=1 530,m=2×13×17=442,m=2×3×13×17=1 326。经验证m=194,m=582,m=1 530,m=442,m=1 326是方程(1)的整数解。

当α=2,ε4=1时,有n4=6,因而有

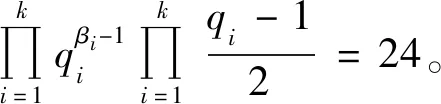
(24)

此时式(24)有解k=2、β1=2、β2=1、q1=3、q2=17与k=2、β1=β2=1、q1=7、q2=17与k=3、β1=β2=β3=1、q1=3、q2=7、q3=17,此时m=22×32×17=612,m=22×7×17=476,m=22×3×7×17=1 428。经验证m=612,m=476,m=1 428是方程(1)的整数解。

当α+ε4=4时,有α=1,ε4=3或者α=2,ε4=2或者α=3,ε4=1,此时φ(η4)=1,有η4=1。

当α=1,ε4=3时,有n4=8,因而有

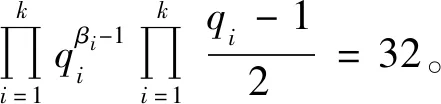
(25)

此时式(25)无奇素数解。

当α=2,ε4=2时,有n4=4,因而有

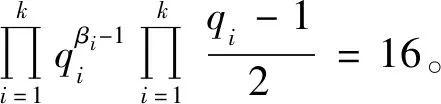
(26)

此时式(26)有解k=2、β1=β2=1、q1=5、q2=17与k=3、β1=β2=β3=1、q1=3、q2=5、q3=17,此时m=22×5×17=340,m=22×3×5×17=1 020。经验证m=340,m=1 020是方程(1)的整数解。

当α=3,ε4=1时,有n4=2,因而有

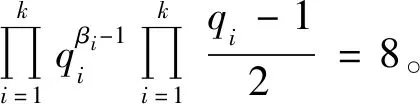
(27)

此时式(27)有解k=1、β1=1、q1=17与k=2、β1=β2=1、q1=3、q2=17,此时m=23×17=136,m=23×3×17=408。经验证m=136,m=408是方程(1)的整数解。

综合以上所有情况的讨论,可得定理1。

3 结 论

对于包含广义Euler函数φ2(m)与广义Euler函数φ4(m)以及函数ω(m)的数论函数方程φ2(φ4(m))=2ω(m)的可解性问题,采用分类分段的方式进行了讨论,得到了数论函数方程φ2(φ4(m))=2ω(m)共有42个正整数解,并给出了其全部的正整数解。